Pythonで因果推論(8)~回帰不連続デザイン(RDD)を用いた効果検証~
はじめに
回帰不連続デザイン(RDD)を用いた因果推論手法について、Pythonによる実装を交えてまとめました。内容について誤り等ございましたら、コメントにてご指摘いただけますと幸いです。
回帰不連続デザイン(RDD)の概要
回帰不連続デザイン(RDD: Regression Discontinuity Design)とは、あるルールによって処置が必ず(あるいは確率的に)割り付けられる際にでも、その因果効果を推定することができる分析手法です。回帰非連続デザインや非連続回帰デザイン・不連続回帰デザインと呼ばれることもあります。
例えば、ある大学の経済学部で選抜試験を行い、選抜試験の得点が合格点を上回った学生だけ計量経済学の特別講義(以下、特講)を受講できる場合の、特講が成績に与える効果を考えます。このとき、合格最低点で特講を受講することができた学生と合格最低点にあと1点届かず特講を受講できなかった学生の間には、能力的には差はないと考えることができると思います。ここで、特講期間を終えた後に計量経済学の試験を行い、合格最低点を取った学生らと合格最低点に1点及ばなかった学生らの試験の得点を比較することで、特講が学生の成績に与える効果を推定するというのが回帰不連続デザイン(RDD)の基本的な考え方です。
横軸に選抜試験の得点、縦軸に特講期間後の試験の得点をプロットした際に、下記の画像のように合格最低点の前後で、特講受講者と特講未受講者で特講後の試験の得点に差があれば、特講の効果があったというように考えることができます。
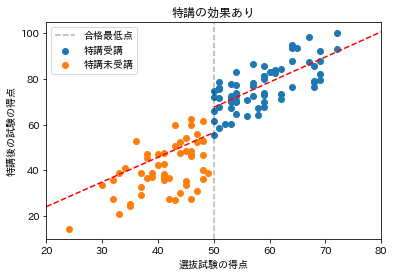
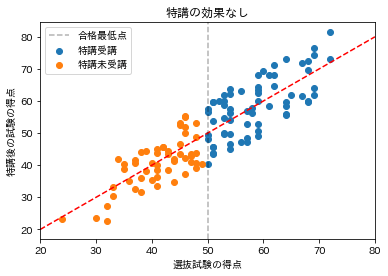
逆に、下記の画像のように合格最低点の前後で、特講受講者と特講未受講者で特講後の試験の得点に差がなければ、特講の効果はなかったというように考えることができます。
回帰不連続デザイン(RDD)には大きく次の2種類に分けられます。
- シャープな回帰不連続デザイン(Sharp RDD): あるルールによって処置が必ず割り当てられる
- ファジーな回帰不連続デザイン(Fuzzy RDD): あるルールによって処置が確率的に割り当てられる
シャープな回帰不連続デザイン(Sharp RDD)
先ほど、選抜試験の得点が合格点を上回った学生だけ計量経済学の特講を受講できる場合を例に挙げました。この例において、処置(特講の受講)の割り当てを決定する変数(選抜試験の得点)のことをランニング変数(running variable)、処置の割り当てを決定する閾値(合格最低点)のことをカットオフ(cut off)と言います。また、合格点を上回った学生が全員特講を受講し、合格点を下回った学生はいかなる場合も特講を受講できないとき、処置が完全遵守されると言い、このときの回帰不連続デザインをシャープな回帰不連続デザイン(Sharp RDD)と言います。
回帰不連続デザイン(RDD)の基本的な考え方は、数式を用いて考えると
- 被説明変数
Y_i - ランニング変数
R_i - カットオフ
C - 処置変数
D_i D_i = 1
とした場合に、選抜試験の得点が合格最低点(
この仮定の下、
- 特講を受講できた学生の得点:
Y_i | R_i = C - 特講を受講できなかった学生の得点:
Y_i | R_i = C - 1
を比較するために、その期待値の差
回帰不連続デザイン(RDD)で推定できる効果は、カットオフ周辺で局所的に平均処置効果(ATE)を算出したものであることから局所的平均処置効果(LATE: Local Average Treatment Effect)になります。
しかし、
そこで実際には、バンド幅
推定に利用する関数形はさまざまなものがありますが、しばしば用いられる関数形として次のようなものが挙げられます。
- 傾きの異なる2つの直線
Y_i = b_0 + b_DD_i + b_1(R_i - C) + b_{d1}D_i \times (R_i - C) + u_i - 形は同じ2つの放物線
Y_i = b_0 + b_DD_i + b_1(R_i - C) + b_2(R_i - C)^2 + u_i - 形の異なる2つの放物線
Y_i = b_0 + b_DD_i + b_1(R_i - C) + b_2(R_i - C)^2 + b_{d1}D_i \times (R_i - C) + b_{d2}D_i \times (R_i - C)^2 + u_i
これらの式を、
ファジーな回帰不連続デザイン(Fuzzy RDD)
先ほど、選抜試験の得点が合格点を上回った学生だけ計量経済学の特講を受講できる場合を例に挙げ、合格点を上回った学生が全員特講を受講し、合格点を下回った学生はいかなる場合も特講を受講できないとき、処置が完全遵守されると言いました。逆に合格点の上回った学生のうち何名かが特講受講を辞退したり、合格点を下回った学生から何名かに特講の受講を許可されるようなとき、処置は完全遵守されないあるいは不完全遵守と表現します。後者の不完全遵守の場合における回帰不連続デザインをファジーな回帰不連続デザイン(Fuzzy RDD)と言います。
回帰不連続デザイン(RDD)の基本的な考え方は、数式を用いて考えると
- 被説明変数
Y_i - ランニング変数
R_i - カットオフ
C - 処置変数
D_i D_i = 1
とした場合に、選抜試験の得点が合格最低点(
全ての学生が選抜試験の得点に従って特講を受講あるいは未受講する場合は
しかし、選抜試験の得点が合格最低点を上回った学生が特講の受講を辞退したり、選抜試験の得点が合格最低点を下回ったものの特別措置的な扱いで特講を受講する学生が存在する場合、上記の計算結果を特講の効果と考えるのは不適切です。
このような場合には、操作変数法(IV法)を利用します。
選抜試験の得点が合格最低点を
- 上回った学生(
R_i \geq C - 下回った学生(
R_i < C
とします。このとき、合格最低点を上回った学生と下回った学生の特講受講確率には2割の差があります。
さらに、合格最低点をギリギリ上回った学生(
ここで、特講受講確率の差が2割から10割(5倍)になれば、特講期間後の試験の得点(
このようにして、カットオフにおける被説明変数の非連続な変化を、処置が割り振られる確率の変化の逆数をかけることで平均処置効果を推定しようとするのがファジーな回帰不連続デザイン(Fuzzy RDD)の考え方です。
以上の内容を操作変数推定量と対応させてまとめると次のようになります。
こちらはカットオフ周辺で局所的に平均処置効果(ATE)を算出したものであることから、局所的平均処置効果(LATE: Local Average Treatment Effect)です。この式が定義できるのは分母が0でない、すなわち
また、選抜試験の結果に従って特講を受講・未受講した学生、すなわち
そのため、ファジーな回帰不連続デザインを実行するためには、
- バンド幅:
h - サンプル:
C-h \leq R_i \leq C+h i - 操作変数:
IV_i R_i \geq C R_i < C - 処置変数(内生変数):
D_i
として、操作変数法(IV法)によって推定することが多いです。
Pythonによる実装
設定(完全遵守)
とある大学の経済学部生120名を対象に選抜試験を行い、選抜試験の得点が51点以上の学生だけ計量経済学の特講を受講できる場合の、特講が成績に与える効果を考えます。選抜試験は不正が生じないものとし、選抜試験に合格した学生はすべて特講を受講するものとします。特講期間が終了したのちに、特講の受講・未受講に関わらず対象者120名に対して計量経済学の試験を実施し、その得点のデータを観測します。
手元には下記のデータが存在するとします。
- 選抜試験の得点
R - 100点満点とし、平均50、標準偏差10の正規分布に従う
- 特講受講ダミー
D - 合格最低点を
C=51 -
R>=C D=1 -
R<C D=0
-
- 合格最低点を
- 試験の得点
Y - 真のモデル
Y_i = \left\{\begin{array}{ll} 60+\frac{R_i}{60}+20D_i+noise & (R_i \geq 60) \\ \\ \frac{-R_i(R_i-120)}{60}+20D_i+noise & (R_i < 60) \end{array}\right. -
noise
- 真のモデル
データの作成
Pythonで上記の設定を満たすデータを作成します。
# 必要なライブラリをインポート
import numpy as np
import pandas as pd
# シードの設定
np.random.seed(0)
# データのサイズ
size = 120
# 選抜試験の得点R(交絡因子)
deviation_value = np.random.normal(50, 10, size)
R = np.clip(deviation_value, 0, 100).astype("int")
_R = np.where(R>60, 60+R/60, -R*(R-120)/60)
# 特講受講ダミーD
D = np.where(R>=51, 1, 0)
# 試験の得点Y
Y_noise = np.random.normal(0, 10, size)
Y = np.clip(_R + 20*D + Y_noise, 0, 100).astype("int")
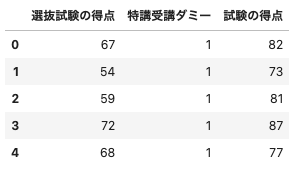
# データフレームに格納し、5つだけ出力
df = pd.DataFrame({"選抜試験の得点": R, "特講受講ダミー": D, "試験の得点": Y})
df.head()
(出力結果)
横軸に選抜試験の得点、縦軸に試験の得点をとって散布図を描画してみます。
# 必要なライブラリとインポート
import matplotlib.pyplot as plt
import japanize_matplotlib
# グラフをJupyter上に描画
%matplotlib inline
# 散布図を描画
plt.scatter(df[df["選抜試験の得点"]<51]["選抜試験の得点"],
df[df["選抜試験の得点"]<51]["試験の得点"], label="特講未受講")
plt.legend()
plt.scatter(df[df["選抜試験の得点"]>=51]["選抜試験の得点"],
df[df["選抜試験の得点"]>=51]["試験の得点"], label="特講受講")
plt.legend()
plt.xlabel("選抜試験の得点")
plt.ylabel("試験の得点")
plt.show()
(出力結果)
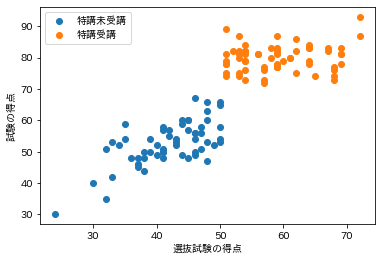
カットオフ(
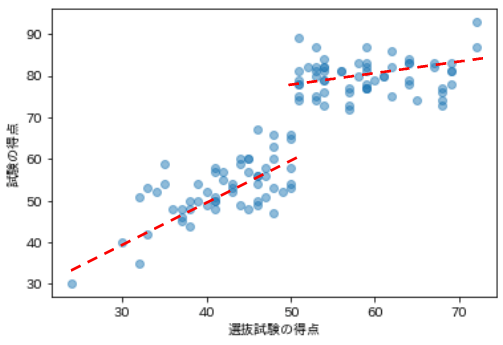
シャープな回帰不連続デザインによる効果検証
線形モデルによる推定
まずは、傾きの同じ線形モデルを仮定して効果を推定してみます。
推定に利用する関数形は
# 必要なライブラリをインポート
import statsmodels.api as sm
# データフレームの調整
df = df.rename(columns={"特講受講ダミー": "D", "試験の得点": "Y"})
df["Rc"] = df["選抜試験の得点"] - 50
df["Rc*D"] = df["Rc"] * df["D"]
df["Rc2"] = df["Rc"]**2
df["Rc2*D"] = df["Rc2"] * df["D"]
# バンド幅を設定し、条件を満たすサンプルだけを取り出す
h = 3
_df = df[(df["Rc"]>=-h) & (df["Rc"]<=h)]
# 説明変数
X = _df[["D", "Rc", "Rc*D"]]
X = sm.add_constant(X)
# 被説明変数
Y = _df["Y"]
# OLS
model = sm.OLS(Y, X)
result = model.fit()
print(result.summary())
(出力結果)
OLS Regression Results
==============================================================================
Dep. Variable: Y R-squared: 0.829
Model: OLS Adj. R-squared: 0.816
Method: Least Squares F-statistic: 60.74
Date: Wed, 13 Jul 2022 Prob (F-statistic): 2.53e-10
Time: 07:41:34 Log-Likelihood: -85.270
No. Observations: 28 AIC: 176.5
Df Residuals: 25 BIC: 180.5
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 58.4052 1.974 29.589 0.000 54.340 62.471
D 19.7263 3.772 5.230 0.000 11.958 27.495
Rc 0.7837 0.946 0.828 0.415 -1.165 2.732
==============================================================================
Omnibus: 1.072 Durbin-Watson: 1.916
Prob(Omnibus): 0.585 Jarque-Bera (JB): 0.962
Skew: 0.249 Prob(JB): 0.618
Kurtosis: 2.241 Cond. No. 8.64
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
効果の推定値を表す
真の値は20なので、効果そのものはよく推定できているようです。
非線形モデルによる推定
まず、傾きの異なる2つの直線である
# 説明変数
X = _df[["D", "Rc", "Rc*D"]]
X = sm.add_constant(X)
# 被説明変数
Y = _df["Y"]
# OLS
model = sm.OLS(Y, X)
result = model.fit()
print(result.summary())
(出力結果)
OLS Regression Results
==============================================================================
Dep. Variable: Y R-squared: 0.830
Model: OLS Adj. R-squared: 0.809
Method: Least Squares F-statistic: 39.12
Date: Wed, 13 Jul 2022 Prob (F-statistic): 2.12e-09
Time: 07:41:04 Log-Likelihood: -85.195
No. Observations: 28 AIC: 178.4
Df Residuals: 24 BIC: 183.7
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 58.8088 2.301 25.553 0.000 54.059 63.559
D 20.1415 4.009 5.024 0.000 11.867 28.416
Rc 1.0662 1.243 0.858 0.399 -1.499 3.631
Rc*D -0.7071 1.966 -0.360 0.722 -4.765 3.351
==============================================================================
Omnibus: 1.432 Durbin-Watson: 1.967
Prob(Omnibus): 0.489 Jarque-Bera (JB): 1.093
Skew: 0.237 Prob(JB): 0.579
Kurtosis: 2.156 Cond. No. 10.4
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
次に、形は同じ2つの放物線
# 説明変数
X = _df[["D", "Rc", "Rc2"]]
X = sm.add_constant(X)
# 被説明変数
Y = _df["Y"]
# OLS
model = sm.OLS(Y, X)
result = model.fit()
print(result.summary())
(出力結果)
OLS Regression Results
==============================================================================
Dep. Variable: Y R-squared: 0.830
Model: OLS Adj. R-squared: 0.809
Method: Least Squares F-statistic: 39.14
Date: Wed, 13 Jul 2022 Prob (F-statistic): 2.11e-09
Time: 07:41:22 Log-Likelihood: -85.189
No. Observations: 28 AIC: 178.4
Df Residuals: 24 BIC: 183.7
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 58.7626 2.226 26.402 0.000 54.169 63.356
D 19.8756 3.860 5.150 0.000 11.910 27.841
Rc 0.7778 0.963 0.808 0.427 -1.210 2.765
Rc2 -0.1067 0.286 -0.373 0.713 -0.697 0.484
==============================================================================
Omnibus: 1.359 Durbin-Watson: 1.965
Prob(Omnibus): 0.507 Jarque-Bera (JB): 1.051
Skew: 0.223 Prob(JB): 0.591
Kurtosis: 2.162 Cond. No. 23.0
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
3つの関数形で効果を推定してみましたが、いずれも似たような推定値に落ち着いており、比較的信憑性のある推定結果が得られました。
設定(不完全遵守)
とある大学の経済学部制120名を対象に選抜試験を行い、選抜試験の得点の合格最低点を51点とします。合格最低点を上回った学生は計量経済学の特講を受講できます。しかし、合格最低点を上回った学生は2割の確率で特講を辞退することが分かっているため、合格最低点を下回った学生に特講受講希望者を募ったところ2割の確率で特講を受講すると回答が得られました。このとき、特講期間が終了した後に、特講の受講・未受講に関わらず対象者120名に対して計量経済学の試験を実施し、その得点のデータを観測することで特講が成績に与える効果を考えます。
手元には下記のデータが存在するとします。
- 選抜試験の得点
R - 100点満点とし、平均50、標準偏差10の正規分布に従う
- 特講受講ダミー
D - 合格最低点を
C=51 -
R>=C D=1 D=0 -
R<C D=0 D=1
-
- 合格最低点を
- 試験の得点
Y - 真のモデル:
Y = R + 20D + noise -
noise
- 真のモデル:
データの作成
Pythonで上記の設定を満たすデータを作成します。
# 必要なライブラリをインポート
import numpy as np
import pandas as pd
# シードの設定
np.random.seed(0)
# データのサイズ
size = 120
# 選抜試験の得点R(ランニング変数)
deviation_value = np.random.normal(50, 10, size)
R = np.clip(deviation_value, 0, 100).astype("int")
# 操作変数
IV = np.where(R>=51, 1, 0)
# 特講受講ダミーD
D = np.array([])
for r in R:
if r >= 51:
d = np.random.choice([0, 1], p=[0.2, 0.8])
else:
d = np.random.choice([0, 1], p=[0.8, 0.2])
D = np.append(D, d)
D = D.astype("int")
# 試験の得点Y
Y_noise = np.random.normal(0, 10, size)
Y = np.clip(R + 20*D + Y_noise, 0, 100).astype("int")
# データフレームに格納し、5つだけ出力
df = pd.DataFrame({"選抜試験の得点": R, "特講受講ダミー": D, "試験の得点": Y, "操作変数": IV})
df.head()
(出力結果)

推定に利用するため、
ファジーな回帰不連続デザインによる効果検証
ファジーな回帰不連続デザイン(Fuzzy RDD)は、カットオフにおける被説明変数の非連続な変化を処置が割り振られる確率の変化の逆数をかけることで効果を推定しようというもので
で計算できます。
# カットオフ前後のデータ
df51 = df[df["選抜試験の得点"]==51]
df50 = df[df["選抜試験の得点"]==50]
# カットオフ前後の試験の平均得点
ey_r51 = df51["試験の得点"].mean()
ey_r50 = df50["試験の得点"].mean()
# カットオフ前後の選抜試験の平均得点
ed_r51 = df51["特講受講ダミー"].mean()
ed_r50 = df50["特講受講ダミー"].mean()
# LATEの算出
(ey_r51 - ey_r50) / (ed_r51 - ed_r50)
(出力結果)
23.521739130434796
真の値が20であるため、多少は上振れしているものの良い推定結果が得られました。
しかし、こちらのアプローチではサンプルサイズ不足が懸念されることが多く、実際にはバンド幅
# バンド幅を設定し、条件を満たすサンプルだけを取り出す
h = 3
C = 51
_df = df[(df["選抜試験の得点"]>=C-h) & (df["選抜試験の得点"]<=C+h)]
_IV = _df["操作変数"]
_Y = _df["試験の得点"]
_D = _df["特講受講ダミー"]
np.sum((_IV - _IV.mean())*(_Y - _Y.mean())) / np.sum((_IV - _IV.mean())*(_D - _D.mean()))
(出力結果)
25.624999999999996
推定値が少し異なる結果となりました。どれくらいの差を許容するかは分析対象によって異なりますが、回帰不連続デザイン(RDD)では真のモデルを知ることはできないので、推定値に大きな差が出る場合は注意が必要です。
参考文献
- 中室、津川「原因と結果の経済学」ダイヤモンド社(2017)
- 岩波データサイエンス刊行委員会編「岩波データサイエンスVol.3-[特集]因果推論-実世界のデータから因果を読む」岩波新書(2016)
- 安井「効果検証入門」ホクソエム社(2020)
- 西山、新谷、川口、奥井「New Liberal Arts Selection 計量経済学」有斐閣(2019)
おわりに
最後まで読んでいただきありがとうございました。他にも「Python×データ分析」をメインテーマに記事を執筆しているので、参考にしていただけたら幸いです。内容の誤り等がございましたら、コメントにてご指摘くださいませ。
他にも下記のような記事を書いています。ご一読いただけますと幸いです。
- 相関関係と因果関係と疑似相関
- 反実仮想と因果効果
- 介入とランダム化比較試験
- 回帰分析を用いた効果検証
- 層別解析を用いた効果検証
- 傾向スコアを用いた効果検証
- 操作変数を用いた効果検証
- 差分の差分法を用いた効果検証
- 機械学習を用いた効果検証
また、過去にLTや勉強会で発表した資料は下記リンクにまとめてあります。ぜひ、ご一読くださいませ。
Discussion