Pythonで因果推論(6)~傾向スコアを用いた効果検証~

はじめに

傾向スコアを用いた因果推論手法について、Pythonによる実装を交えてまとめました。内容について誤り等ございましたら、コメントにてご指摘いただけますと幸いです。

傾向スコア

傾向スコアとは、属性ベクトル$X^i$から予測される処置が施される確率(すなわち、処置を受ける傾向)のことです。

$$P(D^i=1|X^i) = E(D^i|X^i) = e(X^i)$$

と表されます。効果検証にて傾向スコアを利用する際には、

$${Y^i_1,Y^i_0} \perp D^i | e(X^i)$$

という条件付き独立の仮定が満たされている必要です。

因果推論における回帰分析では、条件付き独立の仮定(CIA)

$${Y^i_1,Y^i_0} \perp D^i | X^i$$

が満たされている必要があり、傾向スコアでは条件$X^i$が$e(X^i)$に緩められているものだと覚えておくことをおすすめします。

傾向スコアを用いた因果推論手法はたくさんありますが、本記事では代表的な3つの因果推論手法をご紹介します。

• 傾向スコアマッチング
• 逆確率重み付け法(IPW)
• 二重にロバストな推定法(DR法)

いずれの因果推論手法も傾向スコアを算出するところまでは同じなので、まずはデータを作成し、傾向スコアを算出するところまでPythonで実装します。

設定

とある大学の経済学部生120を対象に、夏季休暇期間に計量経済学の特別講義(特講)を開催し、その効果を考えます。特講は、あくまでも大学の単位とは無関係の任意参加であるため、介入操作が行われない限りは受講するかどうかは学生の属性に依存すると考えます。夏季休暇終了後に、特講の受講にかかわらず対象者120人に対して計量経済学の試験を実施し、その得点のデータを観測します。

手元には下記のデータが存在するとします。

• 学習意欲$X_1$(交絡因子)
  • 学生の学習意欲を0以上1以下の数値で表したもの
  • 一様分布(0, 1)に従う
  • 特講の受講$D$と試験の得点$Y$に影響を与える
• 理系出身ダミー$X_2$(交絡因子)
  • 学生が高校時代、理系だったか文系だったかを表したダミー変数
  • $X_2=1$であれば理系出身、$X_2=0$であれば文系出身
  • 特講の受講$D$と試験の得点$Y$に影響を与える
• 特講受講ダミー$D$(処置変数)
  • 学生が特講を受講したかどうかを表すダミー変数
  • $D=1$であれば特講を受講したことを、$D=0$であれば特講を受講していないことを表す
  • 学習意欲$X_1$と理系出身ダミー$X_2$に依存しており、
    $$0.25 \times X_1 + 0.25 \times X_2 + noise$$
    の値が0.5以上であれば特講を受講($D=1$)、0.5未満であれば特講を未受講($D=0$)とする（ただし、$noise$は一様分布(0, 0.5)に従う）
• 試験の得点$Y$(被説明変数)
  • 学生の試験の得点を表し、真のモデルは
    $$Y = 40 \times X_1 + 20 \times X_2 + 20 \times D + noise$$
    で表現される(ただし、$noise$は、平均0、標準偏差10の正規分布に従う)

特講の受講を表す条件式

$$D = 1 \quad (\:0.25 \times X_1 + 0.25 \times X_2 + noise \geq 0.5\:)$$

$$Z = 0 \quad (\:0.25 \times X_1 + 0.25 \times X_2 + noise < 0.5\:)$$

や試験の得点を表す真のモデル

$$\:Y = 40 \times X_1 + 20 \times X_2 + 20 \times D + noise \:$$

は、分析者は知り得ません。

データの作成

Pythonで上記の設定を満たすデータを作成します。

# 必要なライブラリをインポート
import numpy as np
import pandas as pd

# シードの設定
np.random.seed(0)
# データのサイズ
size = 120

# 学習意欲を表す変数X1(交絡因子)
X1 = np.random.uniform(0, 1, size)
# 理系出身ダミーX2(交絡因子)
X2 = np.random.choice([0, 1], p=[0.5, 0.5], size=size)
# 特講受講ダミーD(処置変数)
D_noise = np.random.uniform(0, 0.5, size)
D_threshold = 0.25*X1 + 0.25*X2 + D_noise
D = np.where(D_threshold>=0.5, 1, 0)

# 試験の得点Y
Y_noise = np.random.normal(0, 10, size)
Y = np.clip(40*X1 + 20*X2 + 20*D + Y_noise, 0, 100).astype("int")

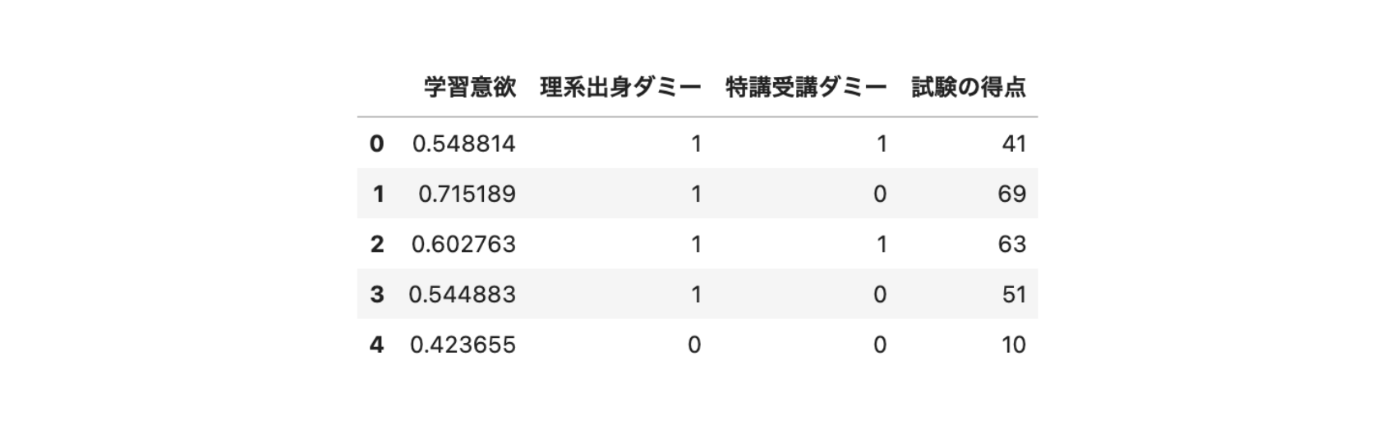
# データフレームに格納し、5つだけ出力
df = pd.DataFrame({"学習意欲": X1, "理系出身ダミー": X2, "特講受講ダミー": D, "試験の得点": Y})
df.head()

(出力結果)

特講受講の有無別に試験の得点の分布を箱ひげ図にて確認してみます。

import matplotlib.pyplot as plt
%matplotlib inline
import japanize_matplotlib

Y0 = df[df["特講受講ダミー"]==0]["試験の得点"]
Y1 = df[df["特講受講ダミー"]==1]["試験の得点"]

plt.title("特講の受講と試験の得点")
plt.boxplot([Y0, Y1], labels=["特講未受講", "特講受講"])
plt.ylabel("試験の得点")
plt.show()

(出力結果)

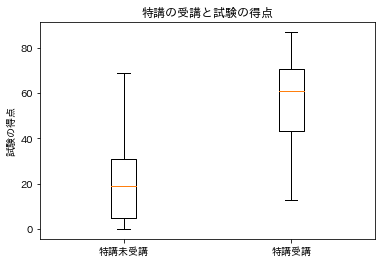
特講を受講しているグループの方が、特講を受講していないグループよりも試験の得点が高い傾向にあることが分かります。

しかし、単純に試験の得点の平均点を比較してしまうと、その差は次のようになります。

Y1.mean() - Y0.mean()

(出力結果)

39.06140594609613

真の値が20なので、特講受講の効果がかなり過大評価されているということが分かります。これは学習意欲$X_1$や理系出身ダミー$X_2$が、特講の受講$D$と試験の得点$Y$の両方に影響を与える交絡因子によってバイアスが生じているためです。そこで傾向スコアを用いた効果検証を行います。

傾向スコアの算出

学習意欲と理系出身ダミーから傾向スコア(特講を受講する確率)を予測するモデルを作成します。そのモデルを利用して、傾向スコアを算出します。今回は傾向スコアを算出するモデルにロジット・モデル(ロジスティック回帰)を利用します。

# 必要なライブラリのインポート
import statsmodels.api as sm

# 傾向スコアを算出するために使用する説明変数
X = df[["学習意欲", "理系出身ダミー"]]
X = sm.add_constant(X)
# 処置変数
D = df["特講受講ダミー"]

# 傾向スコアを算出
model = sm.Logit(D, X)
result = model.fit()
result.predict(X)

(出力結果)

0      0.770041
1      0.841374
2      0.795383
3      0.768111
4      0.192951
         ...   
115    0.181532
116    0.458513
117    0.269884
118    0.458947
119    0.832835
Length: 120, dtype: float64

このあと利用するため、傾向スコアのカラムをデータフレームに追加しておきます。

df["傾向スコア"] = result.predict(X)
df.head()

(出力結果)

これで傾向スコアを用いた効果検証の準備は完了です。

傾向スコアを推定を行ったモデルに対し、特に解釈を行う必要はありません。また、今回はロジット・モデル(ロジスティック回帰)を利用しましたが、プロビット・モデルのような一般化線形モデルや、決定木(ランダムフォレストや勾配ブースティング決定木)のような機械学習モデルを利用することもできます。

傾向スコアによる層化解析法

傾向スコアによる層化解析とは、処置群と対照群の間で属性の似通った(傾向スコアが近い)サンプルを層化してATEを推定する手法です。条件付き独立の仮定のもとでは、平均処置効果(ATE)は

$$ATE = E[Y^i|D^i=1, e(X^i)] - E[Y^i|D^i=0, e(X^i)]= ... = E[Y^i_1 - Y^i_0|e(X^i)]$$

と表すことができ、これを利用します。

下図のように横軸に傾向スコア、縦軸に被説明変数を表す散布図をプロットした際に、まず同じ区間内(隣接する2本の赤い縦線内)で処置群(青)と対照群(オレンジ)の被説明変数の値の平均の差をとります。そして最後に全区間でその平均の差の平均をとってあげることで平均処置効果(ATE)を求めます。

用語の確認(処置変数)

意図的にとある変数を操作(介入)して効果検証を行うという文脈では介入変数と呼ぶことが一般的ですが、必ずしも介入操作が行われていなくても構わないため、便宜上定義した造語です。因果推論のテキストでは「処置変数は原因変数、被説明変数は結果変数」と呼称されていることが多いです。本記事で処置変数・被説明変数と記述しているのは、単なる私の慣習です。

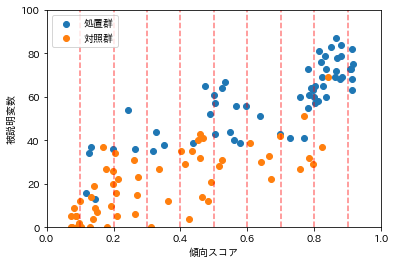
Pythonによる実装

再掲になりますが、条件付き独立の仮定のもとでは、傾向スコアを利用した平均処置効果(ATE)は

$$ATE = E[Y^i|D^i=1, e(X^i)] - E[Y^i|D^i=0, e(X^i)]$$

で表されます。これをPythonで実装します。

# マッチング推定を行う関数の作成
def ps_stratificasion(df, step=0.1):

    scores = np.arange(0, 1, step)

    match_arr = np.array([])
    for score in scores:
        _df = df[(df["傾向スコア"]>=score) & (df["傾向スコア"]<score+step)]
        tmp0 = np.array(_df[_df["特講受講ダミー"]==0]["試験の得点"])
        tmp1 = np.array(_df[_df["特講受講ダミー"]==1]["試験の得点"])
        if (tmp0.size!=0) and (tmp1.size!=0):
            match_arr = np.append(match_arr, tmp1.mean() - tmp0.mean())

    return match_arr.mean()

傾向スコアを0.1刻みでATEを算出します。

ps_stratificasion(df, step=0.1)

(出力結果)

21.42106687172477

真の値が20であるため、かなり近い値で効果を推定できているようです。
傾向スコアの刻み幅を変更すると、推定値も変化します。

# 0.05刻み
print(f"0.05刻み {ps_stratificasion(df, step=0.05)}")
# 0.025刻み
print(f"0.025刻み {ps_stratificasion(df, step=0.025)}")
# 0.01刻み
print(f"0.01刻み {ps_stratificasion(df, step=0.01)}")

(出力結果)

0.05刻み 20.850892857142856
0.025刻み 20.79375
0.01刻み 23.255555555555553

刻み幅は推定値が大きく変化しすぎない程度に変更するのが良さそうです。

逆確率重み付け法(IPW)

逆確率重み付け法(IPW: Inverse Probability Weighting)は、傾向スコアをサンプルの重みとして利用し、処置を受けた場合の結果の期待値($E[Y_1]$)と、処置を受けなかった場合の結果の期待値($E[Y_0]$)を推定し、これらの差分を処置の因果効果として推定する手法です。

ここで、条件付き独立の仮定より

$$E(\frac{D}{e(X)}Y_1) = E_x[E_{D|X}(\frac{D}{e(X)})E_{Y_1|X}(Y_1)] = E[Y_1]$$

であるから、$E[Y_1]$は

$$\frac{1}{N} \sum_{i=1}^N \frac{D^i}{e(X^i)}Y^i$$

として推定されます。同様にして、$E[Y_0]$は

$$\frac{1}{N} \sum_{i=1}^N \frac{1 - D^i}{1 - e(X^i)}Y^i$$

と推定されるので、平均処置効果(ATE)は

$$ATE = E[Y_1] - E[Y_0] = \frac{1}{N} \sum_{i=1}^N \frac{D^i}{e(X^i)}Y^i - \frac{1}{N} \sum_{i=1}^N \frac{1 - D^i}{1 - e(X^i)}Y^i$$

と推定されます。

本記事では上記のように推定しますが、$E[Y_1], E[Y_0]$はそれぞれ

$$\frac{\sum_{i=1}^N \frac{D^i}{e(X^i)}Y^i}{\sum_{i=1}^N \frac{D^i}{e(X^i)}}, \quad \frac{\sum_{i=1}^N \frac{1 - D^i}{1 - e(X^i)}Y^i}{\sum_{i=1}^N \frac{1 - D^i}{1 - e(X^i)}}$$

の方がより変動が小さい推定値であることが知られています（導出は割愛します）

また「なぜ逆確率で重み付けすることによってバイアスなくATEが推定できるのか」については、こちらの記事で直感的な説明をしております。ぜひ、ご参照ください。
https://qiita.com/s1ok69oo/items/ab9c80a353eb45fad78d

Pythonによる実装

再掲になりますが、条件付き独立の仮定のもとでは、傾向スコアを利用した平均処置効果(ATE)は

$$ATE = E[Y_1] - E[Y_0] = \frac{1}{N} \sum_{i=1}^N \frac{D^i}{e(X^i)}Y^i - \frac{1}{N} \sum_{i=1}^N \frac{1 - D^i}{1 - e(X^i)}Y^i$$

で推定されます。これをPythonで実装します。

# IPWの実装
N = len(df)
D = df["特講受講ダミー"]
Y = df["試験の得点"]
e_X = df["傾向スコア"]

# E[Y_1], E[Y_0]を推定
E_Y1 = (1 / N) * np.sum((D / e_X)*Y)
E_Y0 = (1 / N) * np.sum(((1 - D) / (1 - e_X)*Y))

# ATEを算出
E_Y1 - E_Y0

(出力結果)

24.56542657777101

真の値が20であるため、多少上振れしてはいますが、良い推定値が得られているようです。サンプルサイズが大きくなれば、より精緻な推定値が得られるかと思われます。

ちなみに、$E[Y_1], E[Y_0]$をそれぞれ

$$\frac{\sum_{i=1}^N \frac{D^i}{e(X^i)}Y^i}{\sum_{i=1}^N \frac{D^i}{e(X^i)}}, \quad \frac{\sum_{i=1}^N \frac{1 - D^i}{1 - e(X^i)}Y^i}{\sum_{i=1}^N \frac{1 - D^i}{1 - e(X^i)}}$$

で推定した場合には、

# E[Y_1], E[Y_0]を推定
E_Y1 = np.sum((D / e_X)*Y) / np.sum(D / e_X)
E_Y0 = np.sum(((1 - D) / (1 - e_X))*Y) / np.sum((1 - D) / (1 - e_X))
# ATEを算出
E_Y1 - E_Y0

(出力結果)

22.52649384262386

となり、よりよい推定値が得られているようです。

二重にロバストな推定法(DR法)

二重にロバストな推定法(DR法: Doubly Robust Estimator)は、回帰分析で反実仮想の推定値を求め、その推定値と逆確率重み付け法(IPW)を組み合わせて因果効果を推定する手法です。

DR法には頑健性があることが知られており、回帰分析と逆確率重み付け法(IPW)で二重に推定することから、このように呼称されており、

• 回帰モデル
• 傾向スコアの算出モデル

のいずれか一方を正しく設定できていれば、平均処置効果(ATE)をバイアスなく推定することができます。

用語の確認

反実仮想

「実際には〜したが、仮に〜しなかったとしたら...」と、実際の選択とは別の選択をした"if"のケースを想定することを指します。詳細はこちらの記事を参考にしてみてください。

頑健性: robustness

ある統計的手法が必要としている仮定や制約条件を少々満たしていないようなデータにおいても妥当な結果を与えるという性質のことを指します。

先ほど紹介した逆確率重み付け法(IPW)によって推定される平均処置効果(ATE)は次の通りでした。

$$ATE = \frac{1}{N} \sum_{i=1}^N \frac{D^i}{e(X^i)}Y^i - \frac{1}{N} \sum_{i=1}^N \frac{1 - D^i}{1 - e(X^i)}Y^i$$

この式では、特講を受講していた場合$D^i=0$、特講を受講していない場合$D^i-1=0$となるため、すべての$i$($0 \leq i \leq N$)において2項あるうち片方の項は0、すなわち片方の項は推定に利用されていないという風にも考えられます。

そこで、前半の項の$\frac{D^i}{e(X^i)}Y^i$を

$$\frac{D^i}{e(X^i)}Y^i + (1 - \frac{D_i}{e(X^i)})\hat{Y^i_1}$$

後半の項$\frac{1 - D^i}{1 - e(X^i)}Y^i$を

$$\frac{1 - D^i}{1 - e(X^i)}Y^i + (1 - \frac{1 - D^i}{1 - e(X^i)})\hat{Y^i_0}$$

として考えることで、(推定値ではありますが)反実仮想の値を、効果の推定式に盛り込むことができます。

Pythonによる実装

まずは、回帰分析を用いて、反実仮想の値を推定します。

# 必要なライブラリのインポート
import statsmodels.api as sm

# 説明変数
X = df[["学習意欲", "理系出身ダミー", "特講受講ダミー"]]
X = sm.add_constant(X)
# 被説明変数
y = df["試験の得点"]

# モデルの設定(OLS：最小二乗法を指定)
model = sm.OLS(Y, X)
 
# 回帰分析の実行
results = model.fit()

# D=0の場合
X_0 = X.copy()
X_0["特講受講ダミー"] = 0
Y_0 = results.predict(X_0)

# D=1の場合
X_1 = X.copy()
X_1["特講受講ダミー"] = 1
Y_1 = results.predict(X_1)

# 推定値を出力
print(Y_0, Y_1)

(出力結果)

0      39.835272
1      46.459714
2      41.983347
3      39.678782
4      14.995087
         ...    
115    13.914117
116    33.208911
117    21.270829
118    33.234082
119    45.557569
Length: 120, dtype: float64 0      61.214929
1      67.839372
2      63.363004
3      61.058439
4      36.374745
         ...    
115    35.293774
116    54.588569
117    42.650486
118    54.613739
119    66.937227
Length: 120, dtype: float64

こちらを用いて、

$$ATE = \frac{1}{N} \sum_{i=1}^N \{ \frac{D^i}{e(X^i)}Y^i + (1 - \frac{D_i}{e(X^i)})\hat{Y^i_1} \} + \frac{1}{N} \sum_{i=1}^N \{ \frac{1 - D^i}{1 - e(X^i)}Y^i + (1 - \frac{1 - D^i}{1 - e(X^i)})\hat{Y^i_0} \}$$

を計算します。

# DRの実装
N = len(df)
D = df["特講受講ダミー"]
Y = df["試験の得点"]
e_X = df["傾向スコア"]

# DR_Y1, DR_Y0を推定
DR_Y1 = (1 / N) * np.sum((D / e_X)*Y + (1 - (D / e_X))*Y_1)
DR_Y0 = (1 / N) * np.sum(((1 - D) / (1 - e_X))*Y + (1 - ((1 - D) / (1 - e_X)))*Y_0)

# ATEを算出
DR_Y1 - DR_Y0

(出力結果)

20.469465937936086

真の値が20なので、かなり良い推定値が算出できました。

ちなみに、回帰分析で反実仮想における試験の得点を予測した際、このときの特講受講ダミー$D$のパラメータは、回帰分析によって推定された効果を表します。そのため

results.params

を実行して得られる結果

const      -1.873207
学習意欲       39.816128
理系出身ダミー    19.856849
特講受講ダミー    21.379657
dtype: float64

のうち、特講受講ダミーのパラメータは、21.379657です。
また、逆確率重み付け法(IPW)によって推定された効果は、24.56542657777101であることから、二重にロバストな推定法(DR)で得られた効果の方が、回帰分析や逆確率重み付け方(IPW)で得られた効果よりもよく推定できているようです。

参考文献

• 中室、津川「原因と結果の経済学」ダイヤモンド社(2017)
• 岩波データサイエンス刊行委員会編「岩波データサイエンスVol.3-[特集]因果推論-実世界のデータから因果を読む」岩波新書(2016)
• 安井「効果検証入門」ホクソエム社(2020)
• 西山、新谷、川口、奥井「New Liberal Arts Selection 計量経済学」有斐閣(2019)
• 山本「実証分析のための計量経済学」中央経済社(2015)
• Pearl「Causal Inference in Statistics: A Primer」(2016)

おわりに

最後まで読んでいただきありがとうございました。他にも「Python×データ分析」をメインテーマに記事を執筆しているので、参考にしていただけたら幸いです。内容の誤り等がございましたら、コメントにてご指摘くださいませ。

他にも下記のような記事を書いています。ご一読いただけますと幸いです。

• 相関関係と因果関係と疑似相関
• 反実仮想と因果効果
• 介入とランダム化比較試験
• 回帰分析を用いた効果検証
• 層別解析を用いた効果検証
• 操作変数を用いた効果検証
• 回帰不連続デザインを用いた効果検証
• 差分の差分法を用いた効果検証
• 機械学習を用いた効果検証

また、過去にLTや勉強会で発表した資料は下記リンクにまとめてあります。ぜひ、ご一読くださいませ。
https://speakerdeck.com/s1ok69oo