Pythonで因果推論(3)~介入とランダム化比較試験~

はじめに

介入やランダム化比較実験(RCT)について、Pythonによる実装を交えてまとめました。本記事では、グラフ的な表現や調整に関する記述はなく、介入操作の概要と(調整を必要としない)ランダム化比較実験についてのみ取り扱っています。内容について誤り等がありましたら、コメントにてご指摘いただけますと幸いです。

介入

介入とは、「因果推論をする際に、とある変数の値を変化させる操作」のことを表します。そして、多くの場合では介入操作の因果効果を推定することが、その因果推論の目的となっています。

介入操作の具体例

ここで具体例として、こちらの記事で用いた「とある大学に所属する経済学部生の、計量経済学の試験の得点$Y$に対する特別講義(以下、特講)受講$D$の効果」を考えたいと思います。

こちらの記事では、特講の受講するかどうか$D$は学生個人の学習意欲$X$に依存していました。すなわち、学習意欲$X$が高い学生ほど特講を受講し($D=1$)、学習意欲$X$の低い学生は特講を受講しない($D=0$)傾向にあったわけです。ここで注意してほしいのが、この場面では特講を受講する・しないというのは介入ではありません。あくまでも観察によって得られた結果です。このとき、処置群における平均処置効果ATTは

$$ATT = E(Y_1-Y_0|D=1)$$

と表されます。

それに対して、例えば「出席番号がi番未満の学生は特講を受講し($D=1$)、i番以上の学生は特講を受講しない($D=0$)でください」というように、(無理やり)特講の受講を割り当てる場合、特講を受講する・しないというのは介入になります。このとき、介入により研修を受講させたときの効果は、介入操作を表す

$$do(D=1)$$

という数式を用いて

$$E(Y_1-Y_0|do(D=1))$$

と表されます。

$E(\quad|D=1)$と$E(\quad|do(D=1))$は意味が異なるので要注意です。

平均処置効果ATEは

$$ATE = E(Y_1 - Y_0)= E(Y_1) - E(Y_0)$$

で表され、条件付き確率が出てこないため、介入操作を行った場合の効果を表す

$$E(Y_1|do(D=1)) - E(Y_0|do(D=0))$$

の値と等しくなります。

介入操作を行う目的

介入操作を行う目的は、効果を推定しやすくすることにあります。

先ほどの「特講の受講$D$と試験の得点$Y$」を例に挙げます。

本来であれば、学習意欲$X$が高い学生ほど、特講を受講し($D=1)$、試験の得点$Y$も高いという傾向にあります。そのため、特講を受講した学生の方が試験の得点が高い傾向にあるという結果が出ても、それが特講を受講した効果なのか、学生の学習意欲に依る差なのか、正しく評価できないという問題点がありました。

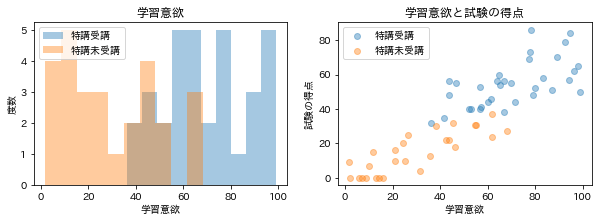
それに対し、介入操作を行うと、学習意欲$X$が高い学生ほど特講を受講する($D=1$)という因果構造がなくなります。そのため、特講を受講した学生と特講を受講していない学生の試験の得点を比較することで、特講の効果を評価できるようになるのです。

実際には「とりあえず介入操作をしておけばOK！」というわけではなく、適切な介入操作を考える必要があります。

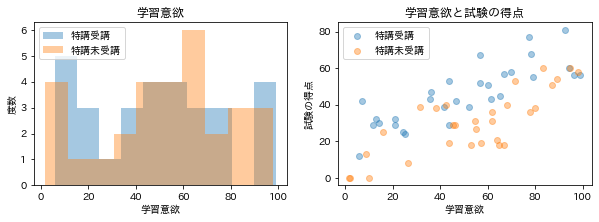
ランダム化比較実験(RCT)

ランダム化比較実験(RCT: Randomized Controlled Trial)とは、介入をランダム(無作為)に割り振って実験し、その結果として得られたデータを比較する分析手法です。

介入の有無をランダムに割り振ることによって、介入が行われるサンプルと行われないサンプルにおけるそのほかの要因も平均的には同一になることが期待できるというのが基本的な考え方です。

先ほどの「特講の受講$D$と試験の得点$Y$」を例に挙げると、特講の受講をランダムに割り振ることによって、特講を受講する($D=1$)学生の学習意欲$X$と特講を受講しない($D=0$)学生の学習意欲$X$の平均が同じくらいになるということですね。

こちらの例を、数式で表現すると

$$E(X_1|do(D=1)) \fallingdotseq E(X_0|do(D=0))$$

ということになります。※$E(\quad|D=d)$は出てきません。

また、RCTについてはこちらの記事もご参照ください。

Pythonによる実装

Pythonで、疑似データを作成し、介入$D$をランダムに割り振り、その結果を比較してみたいと思います。

疑似データの作成

• 学習意欲$X$: 一様分布(0, 100)に従う
• 特講の受講$D$: ランダムに割り振る
• 試験の得点$Y$: 学習意欲$X$と特講の受講$D$に依存する
  • $Y = 0.5X + 20D + noise$
  • $noise$は、正規分布(0, 10)に従う
  • $Y$は、$0 \leq Y \leq 100$を満たす整数

# 必要なライブラリをインポート
import numpy as np
import pandas as pd

# シードの設定
np.random.seed(0)
# でーたのサイズ
size = 60

# 学習意欲を表す変数X
X = np.random.uniform(0, 100, size)
# 特講の受講を表す変数D
D = np.random.choice([0, 1], p=[0.5, 0.5], size=size)

# 試験の得点Y
Y_noise = np.random.normal(0, 10, size)
Y = np.clip(0.5*X + 20*D + Y_noise, 0, 100).astype("int")

# データフレームに格納し、5つだけ出力
df = pd.DataFrame({"学習意欲": X, "特講の受講": D, "試験の得点": Y})
df.head()

(出力結果)

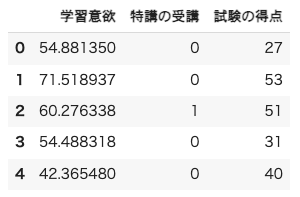
次に介入の割り振られ方を確認してみます。

# 介入の割り振られ方
df["特講の受講"].value_counts()

(出力結果)

0    30
1    30
Name: D, dtype: int64

人数は均等に割り振られていますね。

次に、2群の平均値に注目してみます。

# 2群の平均値の算出
df.groupby(by="特講の受講").mean()

(出力結果)

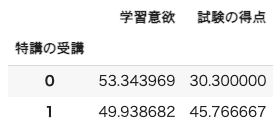
学習意欲$X$の平均はほぼ等しいとまではいきませんがそれほど差がないのに対し、試験の得点$Y$の平均は介入群($D=1$)の方がかなり高いですね。

ヒストグラムも確認してみます。

# 必要なライブラリのインポート
import matplotlib.pyplot as plt
%matplotlib inline
import japanize_matplotlib

# do(D=1)
df_D1 = df[df["特講の受講"]==1]
# do(D=0)
df_D0 = df[df["特講の受講"]==0]

# ヒストグラムの描画
fig = plt.figure(figsize=(10, 3))

# 学習意欲Xのヒストグラム
ax1 = plt.subplot(121)
ax1.hist(df_D1["学習意欲"], alpha=0.4, label="特講受講")
ax1.hist(df_D0["学習意欲"], alpha=0.4, label="特講未受講")
ax1.set_title("学習意欲")

# 試験の得点Yのヒストグラム
ax2 = plt.subplot(122)
ax2.hist(df_D1["試験の得点"], alpha=0.4, label="特講受講")
ax2.hist(df_D0["試験の得点"], alpha=0.4, label="特講未受講")
ax2.set_title("試験の得点")

plt.legend()
plt.show()

(出力結果)

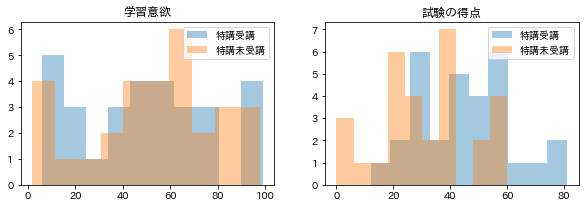
学習意欲$X$は介入に関わらず似たような分布をしていますが、試験の得点$Y$は介入群の方がかなり分布が右に寄っていることが分かりますね。

次に、特講の受講$D$はどれくらい試験の得点$Y$に効果があるかを確認します。介入の効果は

$$E(Y_1|do(D=1)) - E(Y_0|do(D=0))$$

で表されるので、これを計算します。

# 介入の効果
df_D1["特講の受講"].mean() - df_D0["特講の受講"].mean()

(出力結果)

15.466666666666665

よって、特講の受講には、試験の得点を15点上げる効果があるというように解釈できます。

$D$の係数は20であるため、効果の期待値は20に近いほどより正確に推定できていると言えます。ただし、データ生成の過程で、試験の得点が0点以下の場合は0点に繰り上げていたり、数値をint型に変更し小数点以下を切り捨てられる操作が行われていたこともあり、20より下振れした計算結果になっていると考えられます。

今回は明らかに特講の受講に効果があると言えそうですが、一応最後に有意差検定もしておきたいと思います。この場合、試験の得点$Y$のデータに正規性があるとは言い切れないので、有意水準を0.05、帰無仮説を「2群間の平均値に差はない」とし、マン・ホイットニーのU検定で検定します。

# 必要なライブラリをインポート
from scipy import stats

# マン・ホイットニーのU検定
result = stats.mannwhitneyu(df_D1["試験の得点"], df_D0["試験の得点"], alternative="two-sided")
# p値を出力
print(f"p値: {result.pvalue}")

(出力結果)

p値: 0.0015851489181872057

$p < 0.05$なので、帰無仮説は棄却され2群間の平均には差がある、すなわち特講には試験の得点を上げる効果があるということが分かりました。

参考文献

• 中室、津川「原因と結果の経済学」ダイヤモンド社(2017)
• 伊藤「データ分析の力 因果関係に迫る思考法」光文社新書(2017)
• 岩波データサイエンス刊行委員会編「岩波データサイエンスVol.3-[特集]因果推論-実世界のデータから因果を読む」岩波新書(2016)
• 安井「効果検証入門」ホクソエム社(2020)
• 西山、新谷、川口、奥井「New Liberal Arts Selection 計量経済学」有斐閣(2019)
• 山本「実証分析のための計量経済学」中央経済社(2015)
• Pearl「Causal Inference in Statistics: A Primer」(2016)

おわりに

ランダム化比較実験(RCT)は、実際のデータ分析現場で行うということはなかなか現実的ではありませんが、介入について理解する上では非常に有用だと思います。また、介入は因果推論・効果検証を行う上で不可欠と言っても過言ではありません。介入はまだまだ押さえておく必要のある項目が山ほどあるので、少しずつまとめていけたらと思います。

他にも下記のような記事を書いています。ご一読いただけますと幸いです。

• 相関関係と因果関係と疑似相関
• 反実仮想と因果効果
• 回帰分析を用いた効果検証
• 層別解析を用いた効果検証
• 傾向スコアを用いた効果検証
• 操作変数を用いた効果検証
• 回帰不連続デザインを用いた効果検証
• 差分の差分法を用いた効果検証
• 機械学習を用いた効果検証

また、過去にLTや勉強会で発表した資料は下記リンクにまとめてあります。ぜひ、ご一読くださいませ。
https://speakerdeck.com/s1ok69oo