Pythonで因果推論(9)~差分の差分法(DID)による効果検証~
はじめに
差分の差分法(DID)を用いた因果推論手法について、Pythonによる実装を交えてまとめました。内容について誤り等ございましたら、コメントにてご指摘いただけますと幸いです。
差分の差分法(DID)の概要
差分の差分法(DID: Difference In Difference)とは、2時点以上の時点で観測されたデータを利用し、処置の前後で「処置群の平均的な変化(差分)」と「対照群の平均的な変化(差分)」の差分を処置の効果として推定する手法です。
例えば、ある大学の経済学部で計量経済学の特別講義(以下、特講と記載)を開催し、特講が試験の得点に与える効果を考えます。計量経済学の試験は前期と後期に実施され、特講は任意参加で前期試験と後期試験の間に特講が開講されるとします。
このとき、特講を受講した学生のグループ(処置群)と特講を受講しなかった学生のグループ(対照群)の前期試験と後期試験の平均得点の変化(差分)をとります。
- 処置群の平均得点の差分:
Y_{11} - Y_{10} - 対照群の平均得点の差分:
Y_{01} - Y_{00}
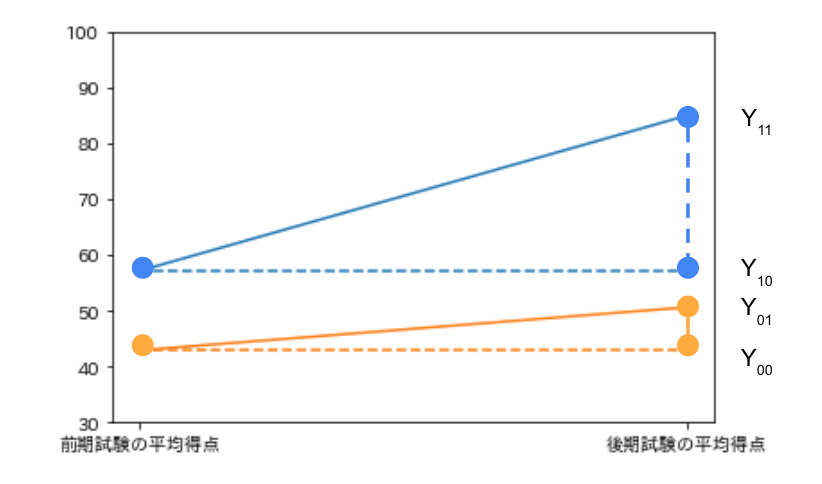
一見すると、処置群の平均得点の差分は特講の効果を表しているように見えますが、実際には特講の効果に加えて特講を受講してもしなくても生じる差(前期試験と後期試験の難易度の違いなど)も含まれています。すなわち
ここで特講を受講した学生のグループ(処置群)が特講を受講しなかった場合、特講を受講しなかったら学生のグループと同じ得点の推移をすると仮定(平行トレンドの仮定)します。特講を受講した学生のグループが特講を受講しなかった場合の平均得点は
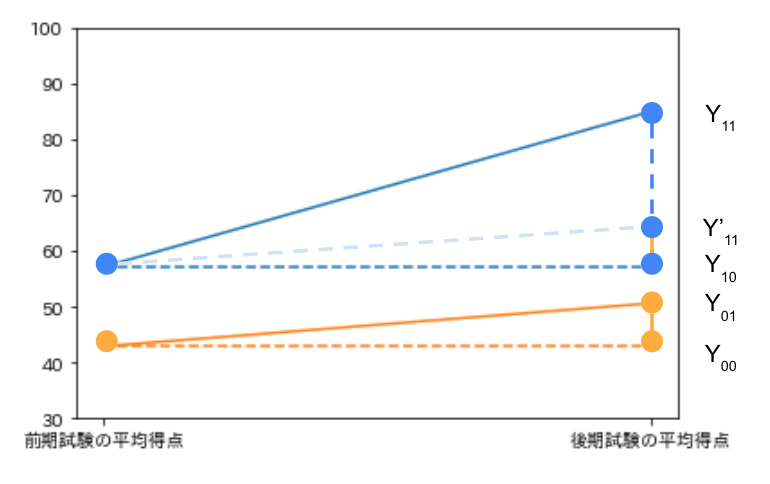
以上から、求めたい特講の効果は
回帰分析による差分の差分法(DID)
差分の差分法(DID)は回帰分析のフレームワークに当てはめることもできます。
先ほどの例を、下記の変数で表現します。
-
Y_{it} -
D_i -
D_i=1 -
D_i=0
-
-
A_t -
t=1 -
t=0
-
推定に利用される回帰モデルの例としては
Pythonによる実装
設定
とある大学の経済学部生120名を対象に計量経済学の試験を前期と後期に実施します。前期と後期の間には特講があり、特講の効果、すなわち特講を受講することによってどれだけ試験の得点が向上するかを推定します。特講には任意で参加することができ、前期試験の得点が高い学生の方が学習意欲が高く特講に参加する傾向にあることが分かっているとします。
手元には下記のデータが存在するとします。
- 前期試験の得点
X - 100点満点とし、平均50、標準偏差10の正規分布に従う
- 特講受講ダミー
D - 平均0、標準偏差10の正規分布に従う
noise D_i = \left\{\begin{array}{ll} 1 & (X_i + noise \geq 50) \\ \\ 0 & (X_i + noise < 50) \end{array}\right.
- 平均0、標準偏差10の正規分布に従う
- 後期試験の得点
Y - 100点満点とし、平均10、標準偏差10の正規分布に従う
noise Y_i = X_i + 20D_i + noise
- 100点満点とし、平均10、標準偏差10の正規分布に従う
データの作成
Pythonで上記の設定を満たすデータを作成します。
# 必要なライブラリをインポート
import numpy as np
import pandas as pd
# シードを設定
np.random.seed(0)
# データのサイズ
size = 120
# 前期試験の得点X
deviation_value = np.random.normal(50, 10, size)
X = np.clip(deviation_value, 0, 100).astype("int")
# 特講受講ダミーD
noise = np.random.normal(0, 10, size)
D = np.where(X+noise>50, 1, 0)
# 後期試験の得点Y
Y_noise = np.random.normal(10, 10, size)
Y = np.clip(X + 20*D + Y_noise, 0, 100).astype("int")
_Y = np.clip(X + Y_noise, 0, 100).astype("int")
# データフレームに格納し、5つだけ出力
df = pd.DataFrame({"前期試験の得点": X, "特講受講ダミー": D, "後期試験の得点": Y})
df.head()
(出力結果)
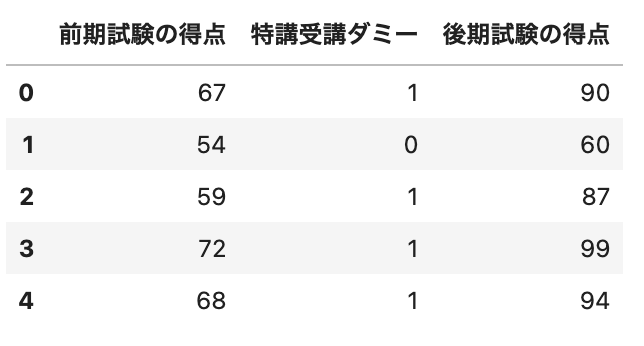
差分の差分法(DID)による効果検証
まずは特講を受講した学生のグループ(処置群)と特講を受講しなかった学生のグループ(対照群)の前期試験・後期試験の平均得点の差の差をとります。
# 処置群(D=1)と対照群(D=0)のグループに分ける
df_D1 = df[df["特講受講ダミー"]==1]
df_D0 = df[df["特講受講ダミー"]==0]
# 処置群と対照群で試験の得点の平均を算出する
before1 = df_D1["前期試験の得点"].mean()
after1 = df_D1["後期試験の得点"].mean()
before0 = df_D0["前期試験の得点"].mean()
after0 = df_D0["後期試験の得点"].mean()
# 差の差を算出する
(after1 - before1) - (after0 - before0)
(出力結果)
20.10785694170655
次に、特講が実施された後である(すなわち、後期試験の結果である)ことを表すダミー変数を
# 必要なライブラリをインポート
import statsmodels.api as sm
# 前期試験・後期試験の得点を1列にまとめる
_Y = pd.concat([df["前期試験の得点"], df["後期試験の得点"]]).reset_index(drop=True)
# _Yのデータに対応するように特講受講ダミーのカラムを作成する
_D = pd.concat([df["特講受講ダミー"], df["特講受講ダミー"]]).reset_index(drop=True)
# 上記のデータをデータフレームにする
_df = pd.DataFrame({"Y": _Y, "D": _D})
# 特講が実施された後であることを表すダミー変数カラムを作成
_df["A"] = 0
_df.loc[120:, "A"] = 1
# 推定する回帰モデルに必要なカラムを作成
_df["D*A"] = _df["D"] * _df["A"]
# 説明変数
_X = sm.add_constant(_df[["D", "A", "D*A"]])
# 被説明変数
_Y = _df["Y"]
# OLSの実施
model = sm.OLS(_Y, _X)
result = model.fit()
# 推定結果の出力
print(result.summary())
(出力結果)
OLS Regression Results
==============================================================================
Dep. Variable: Y R-squared: 0.728
Model: OLS Adj. R-squared: 0.724
Method: Least Squares F-statistic: 210.2
Date: Sun, 24 Jul 2022 Prob (F-statistic): 2.32e-66
Time: 15:23:53 Log-Likelihood: -889.86
No. Observations: 240 AIC: 1788.
Df Residuals: 236 BIC: 1802.
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 42.8868 1.366 31.390 0.000 40.195 45.578
D 14.2326 1.828 7.784 0.000 10.630 17.835
A 7.6981 1.932 3.984 0.000 3.892 11.505
D*A 20.1079 2.586 7.776 0.000 15.014 25.202
==============================================================================
Omnibus: 0.388 Durbin-Watson: 2.104
Prob(Omnibus): 0.824 Jarque-Bera (JB): 0.167
Skew: -0.003 Prob(JB): 0.920
Kurtosis: 3.129 Cond. No. 7.27
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
回帰係数
参考文献
- 中室、津川「原因と結果の経済学」ダイヤモンド社(2017)
- 岩波データサイエンス刊行委員会編「岩波データサイエンスVol.3-[特集]因果推論-実世界のデータから因果を読む」岩波新書(2016)
- 安井「効果検証入門」ホクソエム社(2020)
- 西山、新谷、川口、奥井「New Liberal Arts Selection 計量経済学」有斐閣(2019)
- 山本「実証分析のための計量経済学」中央経済社(2015)
おわりに
最後まで読んでいただきありがとうございました。他にも「Python×データ分析」をメインテーマに記事を執筆しているので、参考にしていただけたら幸いです。内容の誤り等がございましたら、コメントにてご指摘くださいませ。
他にも下記のような記事を書いています。ご一読いただけますと幸いです。
- 相関関係と因果関係と疑似相関
- 反実仮想と因果効果
- 介入とランダム化比較試験
- 回帰分析を用いた効果検証
- 層別解析を用いた効果検証
- 傾向スコアを用いた効果検証
- 操作変数を用いた効果検証
- 回帰不連続デザインを用いた効果検証
- 機械学習を用いた効果検証
また、過去にLTや勉強会で発表した資料は下記リンクにまとめてあります。ぜひ、ご一読くださいませ。
Discussion