Pythonで因果推論(7)~操作変数(IV)を用いた効果検証~

はじめに

操作変数法を用いた因果推論手法について、Pythonによる実装を交えてまとめました。内容について誤り等ございましたら、コメントにてご指摘いただけますと幸いです。

操作変数の概要

操作変数

操作変数(IV: Instrumental Valiable)とは、処置には影響を与えるものの、被説明変数には処置を通してのみしか影響を与えない変数です。

操作変数を用いることで

• 脱落変数バイアス(欠落変数バイアス)
• 同時決定・内生性バイアス

が生じている場合にも、因果効果の推定が可能になります。

用語の確認

• 脱落変数バイアス(欠落変数バイアス)
  本来であれば必要であるがモデルから抜け落ちている脱落変数(欠落変数)が存在することによって生じるバイアス。こちらの記事では、回帰モデルにおいて脱落変数バイアスが生じた例を紹介しています。
• 同時決定・内生性バイアス
  説明変数が被説明変数に影響を与えていると同時に、被説明変数も説明変数に影響を与えている場合に生じるバイアス。逆の因果関係が生じている場合にも生じます。逆の因果については、こちらの記事でも紹介しています。

次のようなモデルのもと、操作変数$IV$を用いてパラメータ$b_D$を推定することを考えます。

$$Y_i = b_0 + b_D D_i + u_i$$

ただし

$$u_i 〜 N(0, \sigma^2), \: Cov(D_i, u_i) ≠ 0$$

このとき、操作変数$IV$が満たす条件は次の通りです。

1. 操作変数$IV$は処置変数$D$と相関がある($Cov(IV_i, D_i) ≠ 0$)
2. 操作変数$IV$は誤差項$u$とは無相関($Cov(IV_i, u_i) = 0$)

上記は、説明変数(内生変数)と操作変数がひとつずつの場合の条件です。一般の場合の操作変数が満たすべき条件はもう少し複雑になるため、本記事では割愛させていただきます。

用語の確認

• 内生変数: 誤差項と相関を持つ変数
• 外生変数: 誤差項と相関を持たない変数

操作変数法

操作変数法(IV法: Instrumental Valiable method)とは操作変数(IV)を用いて処置の被説明変数への因果効果を推定する解析方法です。

先ほどと同様の$Y_i = b_0 + b_D D_i + u_i$というモデルでは、条件を満たす操作変数$IV$を用いてパラメータ$b_D$を次のように推定することができます。

$$\hat{b^{IV}_D} = \frac{Cov(IV, Y)}{Cov(IV, D)} = \frac{\sum_{i=1}^N(IV_i - \bar{IV})(Y_i - \bar{Y})}{\sum_{i=1}^N(IV_i - \bar{IV})(D_i - \bar{D})}$$

こちらは2段階最小二乗法という手法でも算出することができます。

操作変数推定量の導出については、こちらの記事をご参照ください。

2段階最小二乗法

2段階最小二乗法(2SLS: TSLS: Two-Stage Least Squares)とは、その他の通り2段階で最小二乗法(OLS)を実行する推定手法です。

先ほどと同様の$Y_i = b_o + b_DD_i + u_i$というモデルを考えると、操作変数$IV$を用いた2段階最小二乗法は次のような流れでパラメータ$b_D$を推定します。

1段階目

まず、処置変数$D_i$を被説明変数、操作変数$IV_i$を説明変数とする次のような回帰モデルを考えます。

$$D_i = \pi_0 + \pi_{IV}IV + v_i$$

このモデルで最小二乗法(OLS)を実行し、$D_i$の予測値$\hat{D}_i$を算出します。

2段階目

先ほど算出した予測値$\hat{D}_i$を$D_i$に代入します。

$$Y_i = b_o + b_D \hat{D}_i + u_i$$

このモデルで最小二乗法(OLS)を実行して得られたパラメータ$b_D$が、2SLS推定量$\hat{b}^{2SLS}_D$であり、

$$\hat{b}^{2SLS}_D = \frac{\sum_{i=1}^N(\hat{D}_i - \bar{\hat{D}})(Y_i - \bar{Y})}{\sum_{i=1}^N(\hat{D}_i - \bar{\hat{D}})^2}$$

と表されます。

2SLS推定量$\hat{b}^{2SLS}$は操作変数の数が内生変数の数と等しい場合には、操作変数推定量$\hat{b}^{IV}$と等しくなります。また、2SLS推定量$\hat{b}^{2SLS}$は操作変数の数が内生変数の数より多い場合にも用いることができます。

Pythonによる実装

設定

とある大学の経済学部生200人を対象に、夏季休暇期間に計量経済学の特別講義(特講)を開催し、その効果を考えます。特講を開催するにあたって受講対象生(約半数)に対してランダムに特講開催の紹介メールを送信しています。夏季休暇終了後に、特講の受講にかかわらず対象者200人に対して計量経済学の試験を実施し、その得点のデータを観測します。

• 学習意欲$X$(観測不能な交絡因子)
  • 学生の学習意欲を0以上1以下の数値で表したもの
  • 一様分布(0, 1)に従う
  • 特講の受講$D$と試験の得点$Y$に影響を与える
• メール受信ダミー$IV$(操作変数)
  • 特講開催の紹介メールが届いたかどうかを表すダミー変数
  • メールはランダムに割り当てられている
• 特講受講ダミー$D$(処置変数)
  • 学生が特講を受講したかどうかを表すダミー変数
  • $D=1$であれば特講を受講したことを、$D=0$であれば特講を受講していないことを表す
  • 学習意欲$X$とメール受信ダミー$IV$に依存しており、
    $$0.3 \times X + 0.4 \times IV + noise$$
    の値が0.5以上であれば特講を受講($D=1$)、0.5未満であれば特講を未受講($D=0$)とする（ただし、$noise$は一様分布(0, 0.3)に従う）
• 試験の得点$Y$(被説明変数)
  • 学生の試験の得点を表し、真のモデルは
    $$Y = 50 \times X + 20 \times D + noise$$
    で表現される(ただし、$noise$は、平均0、標準偏差10の正規分布に従う)

データの作成

Pythonで上記の設定を満たすデータを作成します。

# 必要なライブラリをインポート
import numpy as np
import pandas as pd

# シードの設定
np.random.seed(0)
# データのサイズ
size = 200

# 学習意欲を表す変数X(観測不能な交絡因子)
X = np.random.uniform(0, 1, size)
# メール送信ダミーIV
IV = np.random.choice([0, 1], p=[0.5, 0.5], size=size)
# 特講受講ダミーD
D_noise = np.random.uniform(0, 0.3, size)
D_threshold = 0.3*X + 0.4*IV + D_noise
D = np.where(D_threshold>=0.5, 1, 0)

# 試験の得点Y
Y_noise = np.random.normal(0, 10, size)
Y = np.clip(50*X + 20*D + Y_noise, 0, 100).astype("int")

# データフレームに格納し、5つだけ出力
df = pd.DataFrame({"メール受信ダミー": IV, "特講受講ダミー": D, "試験の得点": Y})
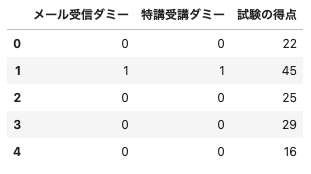
df.head()

(出力結果)

操作変数法による効果検証

本来、試験の得点$Y$に寄与している変数は学習意欲$X$と特講受講ダミー$D$です。さらに学習意欲$X$は特講受講ダミー$D$にも影響を与える交絡因子となっています。しかし、学習意欲$X$は観測不能なため、操作変数$IV$を用いて特講受講ダミー$D$のパラメータを推定します。

$Y_i = b_o + b_DD_i + u_i$というモデルの下で操作変数$IV$を用いると、パラメータ$b_D$は次のように推定できます。

$$\hat{b}_D^{IV} = \frac{\sum_{i=1}^N(IV_i - \bar{IV})(Y_i - \bar{Y})}{\sum_{i=1}^N(IV_i - \bar{IV})(D_i - \bar{D})}$$

これをPythonで計算します。

np.sum((IV - IV.mean())*(Y - Y.mean())) / np.sum((IV - IV.mean())*(D - D.mean()))

(出力結果)

17.011952191235057

$b_D$の真の値は20なので多少下振れした推定値になりました。

今回サンプルサイズ200で推定しましたが、サンプルサイズだけ変更して同じコードを実行してみると推定値にかなりブレがあることがわかります。実際に推定値が安定させるには、かなりのサンプルサイズが必要なようです。

2段階最小二乗法による効果検証

1段階目

まずは、操作変数$IV$を用いて処置変数$D$を推定します。

$$D_i = \pi_0 + \pi_{IV}IV + v_i$$

というモデルでOLSを実行します。

# 必要なライブラリのインポート
import statsmodels.api as sm

# 説明変数
IV = df[["メール受信ダミー"]]
IV = sm.add_constant(IV)
# 被説明変数
D = df["特講受講ダミー"]

# モデルの設定(OLS:最小二乗法を指定)
model1 = sm.OLS(D, IV)

# 推定値を出力
result1 = model1.fit()
result1.predict(IV)

(出力結果)

0      0.066667
1      0.947368
2      0.066667
3      0.066667
4      0.066667
         ...   
195    0.947368
196    0.066667
197    0.066667
198    0.066667
199    0.066667
Length: 200, dtype: float64

これで$D$の推定値$\hat{D}$を算出することができました。

2段階目

$D$の推定値を利用して、パラメータ$b_D$を推定します。

$$Y_i = b_0 + b_D \hat{D} + u_i$$

というモデルでOLSを実行します。

# 説明変数(Dの推定値を利用)
D_hat = result1.predict(IV)
D_hat = sm.add_constant(D_hat)
# 被説明変数
Y = df["試験の得点"]

# モデルの設定(OLS:最小二乗法を指定)
model2 = sm.OLS(Y, D_hat)

# OLSの結果を出力
result2 = model2.fit()
print(result2.params)

(出力結果)

const    24.999203
0        17.011952

これでパラメータ$b_D$は$\hat{b}^{2SLS}_D = 17.011952$と推定されました。この推定結果は先ほど算出した操作変数推定量$\hat{b}^{IV}_D$と同じ値であることが分かります。

参考文献

• 中室、津川「原因と結果の経済学」ダイヤモンド社(2017)
• 岩波データサイエンス刊行委員会編「岩波データサイエンスVol.3-[特集]因果推論-実世界のデータから因果を読む」岩波新書(2016)
• 西山、新谷、川口、奥井「New Liberal Arts Selection 計量経済学」有斐閣(2019)
• 山本「実証分析のための計量経済学」中央経済社(2015)
• 末石「計量経済学 ミクロデータ分析へのいざない」日本評論社(2015)

おわりに

最後まで読んでいただきありがとうございました。他にも「Python×データ分析」をメインテーマに記事を執筆しているので、参考にしていただけたら幸いです。内容の誤り等がございましたら、コメントにてご指摘くださいませ。

他にも下記のような記事を書いています。ご一読いただけますと幸いです。

• 相関関係と因果関係と疑似相関
• 反実仮想と因果効果
• 介入とランダム化比較試験
• 回帰分析を用いた効果検証
• 層別解析を用いた効果検証
• 傾向スコアを用いた効果検証
• 回帰不連続デザインを用いた効果検証
• 差分の差分法を用いた効果検証
• 機械学習を用いた効果検証

また、過去にLTや勉強会で発表した資料は下記リンクにまとめてあります。ぜひ、ご一読くださいませ。
https://speakerdeck.com/s1ok69oo