Pythonで因果推論(5)~層別解析を用いた効果検証~
はじめに
層別解析による因果推論について、Pythonによる実装を交えてまとめました。内容について誤り等ございましたら、コメントにてご指摘いただけますと幸いです。
層別解析の概要
層別解析とは、交絡因子で解析対象を層に分けて、処置変数がどれだけ被説明変数に影響を与えているかを推定する統計解析手法です。
交絡因子が存在していると、被説明変数が変化した際に、
- 処置変数による効果なのか
- 交絡変数が処置変数や被説明変数の両方に影響を与えた結果なのか
が判別できません。そこで、交絡因子を層別に分けることで、擬似的に交絡因子の値を固定されているような状態を作り、処置変数の効果を特定してあげようというイメージです。
Pythonによる実装
自作でデータを作成し、層別解析を実装してみます。
設定
とある大学の経済学部生200人を対象に、夏季休暇期間に計量経済学の特別講義(特講)を開催し、その効果を考えます。特講は、あくまでも大学の単位とは無関係の任意参加であるため、介入操作が行われない限りは受講するかどうかは学生の意欲に依存すると考えます。夏季休暇終了後に、特講の受講にかかわらず対象者200人に対して計量経済学の試験を実施し、その得点のデータを観測します。
説明変数
- 学習意欲
X - 一様分布(0, 100)に従う
- 特講の受講
D - 学習意欲
X -
X + noise \leq 50 D = 0 -
X + noise > 50 D = 1 -
noise
- 学習意欲
被説明変数
- 試験の得点
Y - 学習意欲
X D - 真のモデルは
\:Y = 0.5X + 20D + noise\: -
noise -
Y 0 \leq Y \leq 100
- 学習意欲
上記のデータから
データの作成
Pythonで、上記の設定どおりにデータを作成します。
# 必要なライブラリをインポート
import numpy as np
import pandas as pd
# シードの設定
np.random.seed(0)
# データのサイズ
size = 200
# 学習意欲を表す変数X
X = np.random.uniform(0, 100, size)
# 特講の受講を表す変数D
D_noise = np.random.uniform(-20, 20, size)
D = np.where(X+D_noise>50, 1, 0)
# 試験の得点Y
Y_noise = np.random.normal(20, 10, size)
Y = np.clip(0.4*X + 20*D + Y_noise, 0, 100).astype("int")
# データフレームに格納し、上5つのデータを出力
df = pd.DataFrame({"学習意欲": X, "特講受講ダミー": D, "試験の得点": Y})
df.head()
(出力結果)

データの確認
次にデータの要約統計量を確認します。
df.describe()
(出力結果)

特講受講の有無で試験の得点の分布にどのような違いがあるのかを確認するために、箱ひげ図を描画します。
# 必要なライブラリのインポート
import matplotlib.pyplot as plt
%matplotlib inline
import japanize_matplotlib
# 特講の受講と試験の得点を箱ひげ図で描画
Y1 = df[df["特講受講ダミー"]==1]["試験の得点"]
Y0 = df[df["特講受講ダミー"]==0]["試験の得点"]
plt.title("特講の受講と試験の得点")
plt.boxplot([Y0, Y1], labels=["特講未受講", "特講受講"])
plt.ylabel("試験の得点")
plt.show()
(出力結果)
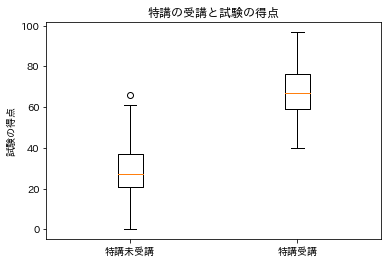
これだけ見ると、特講の受講には効果があると言ってしまいそうですが、グッと堪えて特講の受講の有無に対応した学習意欲や試験の得点のヒストグラムを見て分布を確認します。これは学習意欲が特講の受講と試験の得点における交絡因子になっていないか確認するためです。
# 特講受講ダミーの有無でdfを分割
df_D1 = df[df["特講受講ダミー"]==1]
df_D0 = df[df["特講受講ダミー"]==0]
# ヒストグラムの描画
fig = plt.figure(figsize=(10, 3))
# 学習意欲Xのヒストグラム
ax1 = plt.subplot(121)
ax1.hist(df_D1["学習意欲"], alpha=0.4, label="特講受講")
ax1.hist(df_D0["学習意欲"], alpha=0.4, label="特講未受講")
ax1.set_title("学習意欲")
plt.legend(loc='upper left')
# 試験の得点Yのヒストグラム
ax2 = plt.subplot(122)
ax2.hist(df_D1["試験の得点"], alpha=0.4, label="特講受講")
ax2.hist(df_D0["試験の得点"], alpha=0.4, label="特講未受講")
ax2.set_title("試験の得点")
plt.legend(loc='upper left')
plt.show()
(出力結果)

特講を受講した学生の方が学習意欲・試験の得点ともに高いということが確認できました。そのため、現状では学習意欲が交絡因子になっている可能性が高く、特講を受講した学生と受講していない学生の試験の得点にはバイアスが生じていると思われます。特講の効果を正しく測定するためには交絡因子によるバイアスを取り除いてあげる必要があります。そこで層別解析の出番です。
層別解析の実装
層別解析によってパラメータを推定する前に、まずは全データを用いて
全データを利用してパラメータを推定
Pythonのstatsmodels.apiを利用して、パラメータを推定します。
# 必要なライブラリをインポート
import statsmodels.api as sm
# 推定: y = b0 + bD*D
# 説明変数
X = df[["特講受講ダミー"]]
X = sm.add_constant(X)
# 被説明変数
Y = df["試験の得点"]
# モデルの設定(OLS:最小二乗法を指定)
model = sm.OLS(Y, X)
# 回帰分析の実行
results = model.fit()
# 結果の詳細を表示
print(results.summary())
(出力結果)
OLS Regression Results
==============================================================================
Dep. Variable: 試験の得点 R-squared: 0.711
Model: OLS Adj. R-squared: 0.710
Method: Least Squares F-statistic: 487.5
Date: Mon, 13 Jun 2022 Prob (F-statistic): 2.69e-55
Time: 22:14:35 Log-Likelihood: -786.79
No. Observations: 200 AIC: 1578.
Df Residuals: 198 BIC: 1584.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 28.8776 1.256 23.000 0.000 26.402 31.353
特講受講ダミー 38.8185 1.758 22.080 0.000 35.352 42.286
==============================================================================
Omnibus: 2.383 Durbin-Watson: 1.924
Prob(Omnibus): 0.304 Jarque-Bera (JB): 2.453
Skew: 0.247 Prob(JB): 0.293
Kurtosis: 2.775 Cond. No. 2.64
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
特講受講ダミーの回帰係数を見ると、38.8185と推定されています。真の値は20であるため、効果をかなり過大評価してしまっていることが分かると思います。
層別解析による推定
今度はデータを学習意欲で3層に分けて、層別にパラメータを推定します。まずは3層に分けるための閾値を2つ設定します。
# 閾値を設定
threshold1 = np.percentile(df["学習意欲"], 40)
threshold2 = np.percentile(df["学習意欲"], 70)
print(threshold1, threshold2)
(出力結果)
42.68032399907316 67.9017665488406
閾値を設定したら、データを
- 層0: 学習意欲がthreshold1未満
- 層1: 学習意欲がthreshold1以上、threshold2未満
- 層2: 学習意欲がthreshold2以上
の3層に分けます。そして、層別にパラメータを推定します。summaryを表示しても良いのですが、今回は効果の推定に焦点を当てているため、効果検証に必要な回帰係数と標準誤差だけを出力します。
# 層0のパラメータを推定
_df = df[df["学習意欲"]<threshold1].reset_index(drop=True)
X = _df[["特講受講ダミー"]]
X = sm.add_constant(X)
# 被説明変数
Y = _df["試験の得点"]
# モデルの設定(OLS:最小二乗法を指定)
model = sm.OLS(Y, X)
# 回帰分析の実行
results = model.fit()
# 回帰係数と標準偏差をそれぞれ変数に格納し、出力
b0 = results.params["特講受講ダミー"]
se0 = results.bse["特講受講ダミー"]
print(f"回帰係数: {b0}")
print(f"標準誤差: {se0}")
(出力結果)
回帰係数: 32.94736842105266
標準誤差: 5.109723693802311
これだけ見ると、あまり良い推定ができそうには見えませんね。笑
同様に層1,2のパラメータも推定します。少し長いですが、コードの中身はほとんど同じです。
# 層1のパラメータを推定
_df = df[(df["学習意欲"]>=threshold1) & (df["学習意欲"]<threshold2)].reset_index(drop=True)
X = _df[["特講受講ダミー"]]
X = sm.add_constant(X)
# 被説明変数
Y = _df["試験の得点"]
# モデルの設定(OLS:最小二乗法を指定)
model = sm.OLS(Y, X)
# 回帰分析の実行
results = model.fit()
# 回帰係数と標準偏差をそれぞれ格納
b1 = results.params["特講受講ダミー"]
se1 = results.bse["特講受講ダミー"]
print(f"層1の回帰係数: {b1}")
print(f"層1の標準誤差: {se1}")
print("----------")
# 層2のパラメータを推定
_df = df[df["学習意欲"]>=threshold2].reset_index(drop=True)
X = _df[["特講受講ダミー"]]
X = sm.add_constant(X)
# 被説明変数
Y = _df["試験の得点"]
# モデルの設定(OLS:最小二乗法を指定)
model = sm.OLS(Y, X)
# 回帰分析の実行
results = model.fit()
# 回帰係数と標準偏差をそれぞれ格納
b2 = results.params["特講受講ダミー"]
se2 = results.bse["特講受講ダミー"]
print(f"層2の回帰係数: {b2}")
print(f"層2の標準誤差: {se2}")
(出力結果)
層1の回帰係数: 20.117216117216117
層1の標準誤差: 2.6957987297632084
-----------
層2の回帰係数: 26.4915254237288
層2の標準誤差: 12.807124078660006
これで各層の回帰係数と標準誤差が推定されました。最後にこれらの回帰係数をその分散(ここでは、標準誤差の2乗)の逆数で重みをつけた平均を取ってあげると、求めたいパラメータ
# 推定値の算出
inv_v0 = 1 / se0**2
inv_v1 = 1 / se1**2
inv_v2 = 1 / se2**2
b_hat = (inv_v0 * b0 + inv_v1 * b1 + inv_v2 * b2) / (inv_v0 + inv_v1 + inv_v2)
b_hat
(出力結果)
23.030766983356447
真の値は20なので、多少上振れしてはいますが、全データを使って一気に推定した時とは比べ物にならないくらい真の値に近い値で効果を推定することができました。
層別解析の弱点
比較的、直感的にも理解しやすく有用な層別解析ですが、弱点もあります。それは「サンプルサイズが足りないと正確な分析が困難である」という点です。とくに、層別にする要素数が増えると、この問題はより深刻になるので注意が必要です。
参考文献
- 中室、津川「原因と結果の経済学」ダイヤモンド社(2017)
- 岩波データサイエンス刊行委員会編「岩波データサイエンスVol.3-[特集]因果推論-実世界のデータから因果を読む」岩波新書(2016)
おわりに
最後まで読んでいただきありがとうございました。他にも「Python×データ分析」をメインテーマに記事を執筆しているので、参考にしていただけたら幸いです。内容の誤り等がございましたら、コメントにてご指摘くださいませ。
他にも下記のような記事を書いています。ご一読いただけますと幸いです。
- 相関関係と因果関係と疑似相関
- 反実仮想と因果効果
- 介入とランダム化比較試験
- 回帰分析を用いた効果検証
- 傾向スコアを用いた効果検証
- 操作変数を用いた効果検証
- 回帰不連続デザインを用いた効果検証
- 差分の差分法を用いた効果検証
- 機械学習を用いた効果検証
また、過去にLTや勉強会で発表した資料は下記リンクにまとめてあります。ぜひ、ご一読くださいませ。
Discussion
一連のブログシリーズ、大変参考になります!D=1 b_D
本記事について一点お伺いしたいのですが、層2(学習意欲が67.9以上の集団)については、箱ひげ図やヒストグラムを見る限り、「特別講義を未受講」のサンプルが含まれていないのかな?とお見受けしました。
もしそれが正しい場合、層2のデータには