PythonによるX-Learnerの実装

はじめに

X-Learnerについて、Pythonによる実装を交えてまとめました。内容について誤り等ございましたら、コメントにてご指摘いただけますと幸いです。

機械学習を用いた因果推論

機械学習を用いた因果推論手法は大きく分けて下記の2通りが存在します。

• Meta-Learner系
• Causal-Tree系

今回はMeta-Learner系の手法の1つであるX-Learnerについて紹介します。

Meta-Leanrerとは

Meta-Learnerとは、機械学習と因果推論の考え方を掛け合わせて条件付き平均処置効果(CATE: Conditional Average Treatment Effect)を推定する手法の総称です。

条件付き平均処置効果(CATE)とは、平均処置効果(ATE: Average Treatment Effect)をある条件($X=x$)に限定して算出したものであり、処置を実施した場合の結果を$Y(1)$、処置を実施しなかった場合を結果$Y(0)$とすると

$$\hat{\tau}(x) = E[Y(1)-Y(0)|X=x] = E[Y(1)|X=x] - E[Y(0)|X=x]$$

で与えられます。X=xについて条件付けした場合の効果を推定するため、個体の属性における効果の異質性、すなわちxによって効果が異なるような非線形な効果も捉えることができます。

ここで、$X=x$の条件である処置を実施した場合、$Y(1)|X=x \:$のデータは取れますが、$Y(0)|X=x \:$のデータは取れません。逆に$X=x$の条件である処置を実施しなかった場合、$Y(0)|X=x \:$のデータは取れますが、$Y(1)|X=x \:$のデータは取れません。

そのため、機械学習を使って取得できないデータの予測値を算出し、推定に利用しようとするのがMeta-Learnerの考え方です。その中でも今回はX-Learnerについて紹介します。

Meta-Learnerの手法には、X-Learnerの他にも

• T-Learner
• S-Learner
• DA-Learner
• DR-Learner

など、さまざまな手法があります。

X-Learnerとは

X-Learnerは、T-Learnerの結果を傾向スコアを用いて補正し、条件付き平均処置効果(CATE)を推定しようとする手法です。

ダイエット商品の広告を回した際に

• iさんの共変量: $X_i$
• iさんが広告を見たかどうか(処置): $T_i$($T_i=1$であれば広告を見た、$T_i=0$であれば広告を見てない)
• iさんの売上: $Y_i$

というデータから広告の効果を推定するという例をもとにX-Learnerの手順を説明します。

1. 処置を受けていない、すなわち、広告を見ていない($T=0$)グループの共変量$X=x$を用いて、処置を受けていない(広告を見ていない)場合の売上($Y(0)$)を予測する回帰モデル$\mu_0(x)$を作成します。
   $$\hat{\mu}_0(x) = M_1(Y^0 \sim X^0)$$
2. 処置を受けた、すなわち、広告を見た($T=1$)グループの共変量$X=x$を用いて、処置を受けた(広告を見た)場合の売上($Y(1)$)を予測する回帰モデル$\mu_1(x)$を作成します。
   $$\hat{\mu}_1(x) = M_2(Y^1 \sim X^1)$$
3. 処置を受けていない($T=0$)グループのデータと処置を受けた場合の売上を予測する回帰モデル$\mu_1(x)$を用いて処置効果$D^0$(ATT)を推定し、推定された処置効果(ATT)を目的変数として回帰モデル$\tau_0(x)$を作成します。
   $$\hat{D}^0 = \hat{\mu}_1(X^0) - Y^0, \: \hat{\tau}_0 = M_3(\hat{D}^0 \sim X^0)$$
4. 処置を受けた($T=0$)グループのデータと処置を受けていない場合の売上を予測する回帰モデル$\mu_0(x)$を用いて処置効果$D^1$(ATU)を推定し、推定された処置効果(ATU)を目的変数として回帰モデル$\mu_3(x)$を作成します。
   $$\hat{D}^1 = Y^0 - \hat{\mu}_0(X^1), \: \hat{\tau}_1 = M_4(\hat{D}^1 \sim X^1)$$
5. 全データから傾向スコアを算出します。ここで傾向スコアを予測するモデルを$g(x)$とします。
6. 全データをモデル$\tau_0(x), \: \tau_1(x)$で予測した効果を傾向スコアで調整し、効果$\tau_X$を推定します。
   $$\hat{\tau} = g(x) \hat{\tau}_0(x) + (1-g(x)) \hat{\tau}_1(x)$$

売上$Y$を予測する回帰モデルの構築にはどのような機械学習手法を用いても構いません。
逆に言えば、機械学習手法の選択によって予測精度に大きな違いが生じるため、手元にあるデータを見ながらどの機械学習手法を選択するのかは考えたり、複数のモデルを作成して推定値にばらつきがないかを確かめる必要があります。

Pythonによる実装

ダイエット商品の広告効果を例に、Pythonでデータを作成し、X-Learnerを用いて効果を算出してみます。

設定

とある健康食品会社では、ECにてダイエット商品を販売しています。ダイエット商品の販促のため広告を回した結果から広告効果を推定することになりました。

手元には下記のデータがあります。

• iさんのダイエットへの意識の高さを表す指標$x_i$
  • 一様分布(-1, 1)に従う
• iさんが広告を見たかどうかを表すダミー変数$T_i$
  • 下記のモデルによって決定されるとする
    $$T_i = \left\{\begin{array}{ll} 1 & (x_i + noise_i > 0): 広告を見た \\ \\ 0 & (x_i + noise_i \leq 0): 広告を見てない \end{array}\right.$$
  • $noise_i$は標準正規分布に従う
• iさんの購入金額$Y_i$
  • $x_i$と$T_i$の影響を受け、真のモデルは下記のように表される
    $$Y_i = 1000(\: [\: 3 + \tau_i T_i + 3x_i + noise_i \:] \: )$$
  • ただし$[x]$は、$n \leq x < n+1$を満たす整数nを表す
  • また、効果$\tau_i$は$x_i$によって異なる
    $$\tau_i = \left\{\begin{array}{ll} 1 & (x_i \leq 0) \\ \\ 2 & (0 < x_i \leq 0.5) \\ \\ 3 & (0.5 < x_i \leq 1) \end{array}\right.$$
  • $noise_i$は一様分布(0, 1)に従う

データの作成

Pythonで上記の設定を満たすデータを作成します。

# 必要なライブラリをインポート
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
# グラフをJupyter上に描画
%matplotlib inline

# データ数
size = 1000
# シードの設定
np.random.seed(0)

# ダイエットへの意識の高さ
x = np.random.uniform(-1, 1, size)
noise = np.random.randn(size)

# 広告ダミー
_T = x + noise
T = np.where(_T>0, 1, 0)

# ダイエットへの意識の高さによって広告効果が異なる
t = np.zeros(size)
for i in range(size):
    if x[i] < 0:
        t[i] = 1
    elif x[i] < 0.5:
        t[i] = 2
    else:
        t[i] = 3
        
# 売上
noise = np.random.uniform(0, 1, size)
Y = np.clip(t*T + 3*x + 3 + noise, 0, 10).astype("int") * 1000

# 売上のヒストグラムを描画
plt.hist(Y)
plt.xlabel("ダイエット商品の売上(単位:円)")
plt.show()

(出力結果)

上記の例では、便宜上ほとんどの人が商品を購入してくれているデータを作成していますが、現実で上図のようなヒストグラムになることはありません。高い割合で商品は購入されず、下図のようなヒストグラムになることが多いです。

X-Learnerによる効果検証

今回は売上$Y$を予測するモデルにランダムフォレストを選択して、効果を推定していきます。

# 必要なライブラリをインポート
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LogisticRegression

# 手順1: 広告を見ていないグループの回帰モデルを作成
df_t0 = df[df["T"] == 0]
mu0 = RandomForestRegressor(max_depth=3, random_state=0)
mu0.fit(df_t0[["x"]], df_t0["Y"])

# 手順2: 広告を見たグループの回帰モデルを作成
df_t1 = df[df["T"] == 1]
mu1 = RandomForestRegressor(max_depth=3, random_state=0)
mu1.fit(df_t1[["x"]], df_t1["Y"])

# 手順3: ATTを求める回帰モデルを作成
tau0 = mu1.predict(df_t0[["x"]]) - df_t0["Y"]
mu2 = RandomForestRegressor(max_depth=3, random_state=0)
mu2.fit(df_t0[["x"]], tau0)

# 手順4: ATUを求める回帰モデルを作成
tau1 = df_t1["Y"] - mu0.predict(df_t1[["x"]])
mu3 = RandomForestRegressor(max_depth=3, random_state=0)
mu3.fit(df_t1[["x"]], tau1)

# 手順5: 傾向スコアを算出
lr = LogisticRegression().fit(df[["x"]], T)
ps = lr.predict_proba(df[["x"]])[:, 1]

# 手順6: 予測した効果を傾向スコアで調整
tau = ps*mu2.predict(df[["x"]]) + (1 - ps)*mu3.predict(df[["x"]])

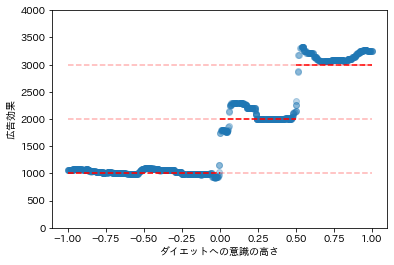
# 推定された効果の描画
plt.scatter(df[["x"]], tau, alpha=0.3)
plt.hlines(1000, -1, 0, linestyles='--', color="red")
plt.hlines(1000, -1, 1, linestyles='--', color="red", alpha=0.3)
plt.hlines(2000, 0, 0.5, linestyles='--', color="red")
plt.hlines(2000, -1, 1, linestyles='--', color="red", alpha=0.3)
plt.hlines(3000, 0.5, 1.0, linestyles='--', color="red")
plt.hlines(3000, -1, 1, linestyles='--', color="red", alpha=0.3)
plt.xlabel("ダイエットへの意識の高さ")
plt.ylabel("広告効果")
plt.ylim(0, 4000)
plt.show()

(出力結果)

EconMLの紹介

EconMLとは、観察可能なデータから機械学習を用いて条件付き平均処置効果(CATE)を推定するPythonパッケージです。Microsoft社が開発しているもので、さまざまなMeta-Learner系やCausal-Tree系の因果推論手法が実装されています。

EconMLの公式ドキュメントはこちらです。
https://econml.azurewebsites.net/

EconMLの公式ドキュメントでは、

EconML is a Python package for estimating heterogeneous treatment effects from observational data via machine learning.

と記載されており、「異質介入効果(HTE: Heterogeneous Treatment Effects)を推定するPythonパッケージである」と書かれてありますが、異質介入効果(HTE)と条件付き平均処置効果(CATE)は同じと思っていただいて問題ないです。そのため、推定したい効果の呼称は"条件付き平均処置効果(CATE)"で統一します。

EconMLによるX-Learnerの実装

X-Learnerは推定に利用する機械学習モデルを選択するだけで実装できます。
今回はランダムフォレスト回帰をモデルに選択します。

# 必要なライブラリのインポート
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LogisticRegression
from econml.metalearners import XLearner

# モデルの構築
models = RandomForestRegressor(max_depth=3, random_state=0)
propensity_model = LogisticRegression()
X_learner = XLearner(models=models, propensity_model=propensity_model)
X_learner.fit(Y, T, X=x.reshape(-1, 1))

# 効果の推定
tau = X_learner.effect(x.reshape(-1, 1))

# 推定された効果の可視化
plt.scatter(df[["x"]], tau, alpha=0.3)
plt.hlines(1000, -1, 0, linestyles='--', color="red")
plt.hlines(1000, -1, 1, linestyles='--', color="red", alpha=0.3)
plt.hlines(2000, 0, 0.5, linestyles='--', color="red")
plt.hlines(2000, -1, 1, linestyles='--', color="red", alpha=0.3)
plt.hlines(3000, 0.5, 1.0, linestyles='--', color="red")
plt.hlines(3000, -1, 1, linestyles='--', color="red", alpha=0.3)
plt.xlabel("ダイエットへの意識の高さ")
plt.ylabel("広告効果")
plt.ylim(0, 4000)
plt.show()

(出力結果)

先ほどと同様の結果が得られました。

先ほどの結果はこちらです。

補足

先ほども少し触れましたが、現実社会においては広告効果を推定したい場合、広告を見た人もそうでない人もその多くが商品を購入しないというシーンがほとんどです。

先ほどの例で売上$Y$の真のモデルを

$$Y_i = 1000(\: [\: \tau_i T_i + 3x_i + noise_i \:] \: )$$

とし、Pythonで実装すると下記のようになります。

# 必要なライブラリをインポート
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
# グラフをJupyter上に描画
%matplotlib inline

# データ数
size = 1000
# シードの設定
np.random.seed(0)

# ダイエットへの意識の高さ
x = np.random.uniform(-1, 1, size)
noise = np.random.randn(size)

# 広告ダミー
_T = x + noise
T = np.where(_T>0, 1, 0)

# ダイエットへの意識の高さによって広告効果が異なる
t = np.zeros(size)
for i in range(size):
    if x[i] < 0:
        t[i] = 1
    elif x[i] < 0.5:
        t[i] = 2
    else:
        t[i] = 3
        
# 売上
noise = np.random.uniform(0, 1, size)
Y = np.clip(t*T + 3*x + noise, 0, 10).astype("int") * 1000
# Y = np.clip(t*T + 3*x + 3 + noise, 0, 10).astype("int") * 1000

# 売上のヒストグラムを描画
plt.hist(Y)
plt.xlabel("ダイエット商品の売上(単位:円)")
plt.show()

(出力結果)

このデータにおいて、X-Learnerを実装してみます。

# 必要なライブラリをインポート
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LogisticRegression
from econml.metalearners import XLearner

# モデルの構築
models = RandomForestRegressor(max_depth=3, random_state=0)
propensity_model = LogisticRegression()
X_learner = XLearner(models=models, propensity_model=propensity_model)
X_learner.fit(Y, T, X=x.reshape(-1, 1))

# 効果の推定
tau = X_learner.effect(x.reshape(-1, 1))

# 推定された効果の可視化
plt.scatter(df[["x"]], tau, alpha=0.3)
plt.hlines(1000, -1, 0, linestyles='--', color="red")
plt.hlines(1000, -1, 1, linestyles='--', color="red", alpha=0.3)
plt.hlines(2000, 0, 0.5, linestyles='--', color="red")
plt.hlines(2000, -1, 1, linestyles='--', color="red", alpha=0.3)
plt.hlines(3000, 0.5, 1.0, linestyles='--', color="red")
plt.hlines(3000, -1, 1, linestyles='--', color="red", alpha=0.3)
plt.xlabel("ダイエットへの意識の高さ")
plt.ylabel("広告効果")
plt.ylim(0, 4000)
plt.show()

(出力結果)

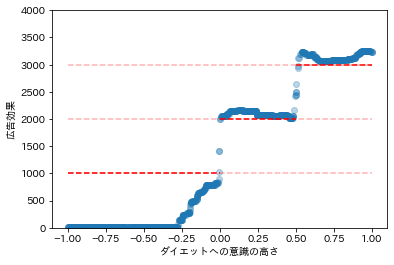
特にダイエットへの意識が低いグループの広告効果において、推定の精度がかなり悪いようです。

上記の例はデータ作成の仕様上起こった問題の1パターンでしかありませんが、現実では推定結果にバイアスが生じていることだらけです。そのため、1つの手法で安易に推定結果を評価せず、複数の手法を用いて慎重に推定結果を評価する必要があります。

参考文献

• EconML公式ドキュメント
• CausalML公式ドキュメント
• Causal Inference for The Brave and True
• Sören R. Künzel, Jasjeet S. Sekhon, Peter J. Bickel, Bin Yu 「Meta-learners for Estimating Heterogeneous Treatment Effects using Machine Learning」(2017)

おわりに

最後まで読んでいただきありがとうございました。他にも「Python×データ分析」をメインテーマに記事を執筆しているので、参考にしていただけたら幸いです。内容の誤り等がございましたら、コメントにてご指摘くださいませ。

他にも下記のような記事を書いています。ご一読いただけますと幸いです。

• 相関関係と因果関係と疑似相関
• 反実仮想と因果効果
• 介入とランダム化比較試験
• 回帰分析を用いた効果検証
• 層別解析を用いた効果検証
• 傾向スコアを用いた効果検証
• 操作変数を用いた効果検証
• 回帰不連続デザインを用いた効果検証
• 差分の差分法を用いた効果検証
• 機械学習を用いた効果検証

また、過去にLTや勉強会で発表した資料は下記リンクにまとめてあります。ぜひ、ご一読くださいませ。
https://speakerdeck.com/s1ok69oo