F.パラメータの更新
この記事では、損失関数を用いて勾配降下法を実践するにあたり鍵となるパラメータの更新について説明しています。SGD,Momentum,Adagradなどのモデルとの比較もしています。
はじめに
E.勾配消失問題 の記事では、「損失関数」と「活性化関数」を調節することで勾配消失問題が回避できることについて解説しました。また、重みの初期化、正規化、学習率の値の調整をすることでも勾配消失を起こしづらくすることができることを説明しました。
損失関数の形をいじる方は「構造的に」学習が進みづらくする要因を防ぐアプローチということができます。対して、今回扱う内容は構造自体の改変は行いません。代わりに、与えられた損失関数の中でいかにして効率的に最小値にたどり着くことができるかを考えます。
パラメータの更新の仕方を工夫することで最小値により高い精度で辿り着くことができます。
勾配降下法で陥る可能性がある問題点
以下のような場合を考えてみましょう。
一回目の更新
Step1.初期位置での勾配を見てみると、左向きにかなり急に傾いていることが分かります。
Step2.ですので、今回は値の更新は大きく大きくなります。
ニ回目の更新
Step1.初めのときとは違って今度は右肩下がりのグラフになっています。
Step2.一回目よりは傾きが緩やかなので、値の更新は少し控えめになります。
到達地点

一回目、二回目に比較してかなり傾きが穏やかになっています。
局所最適解の問題
一見、ここまでの流れを見ていると、順調に最小値に向かっているように見えますが、実は必ずしもそうなっているとは限りません。コンピュータの判断は局所的なのでここまでの値の更新が大局的には正しくない点へと向かってしまうことも起こりえてしまうのです。
例えば、一回目と二回目の座標を黒丸で、到達地点の座標を赤丸で表すとすると下のグラフのように値が更新されている場合もあり得ます。
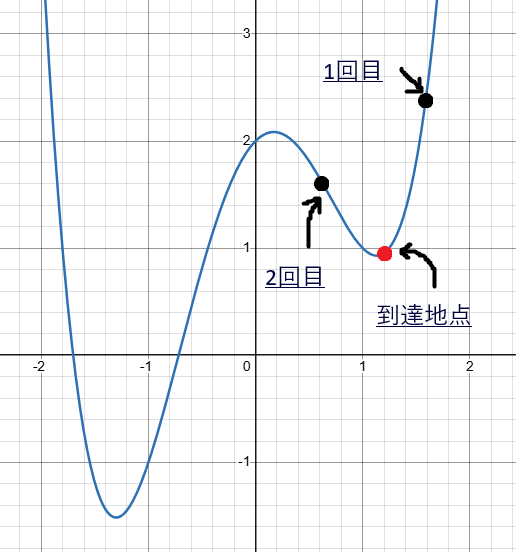
このように近辺の値の中では最小値となっている部分を 局所最適解 といいます。勾配降下法の値の更新の仕方を工夫しないと、この方法では局所最適解にトラップされて関数全体の最小値にたどり着けない事態を避けることができなくなってしまうのです。
学習率の変更
パラメータの更新に使用する式の中で、パラメータの更新の大きさを決めるパラメータのことを 学習率といいます。学習率のようなハイパーパラメータは与えられるものではなく、プログラムを実行する側が指定することができるので、この値を変更することで値の更新をする大きさを調整することができます。
学習率の値を変更したときの 二回目 の値の変化を可視化してみます。
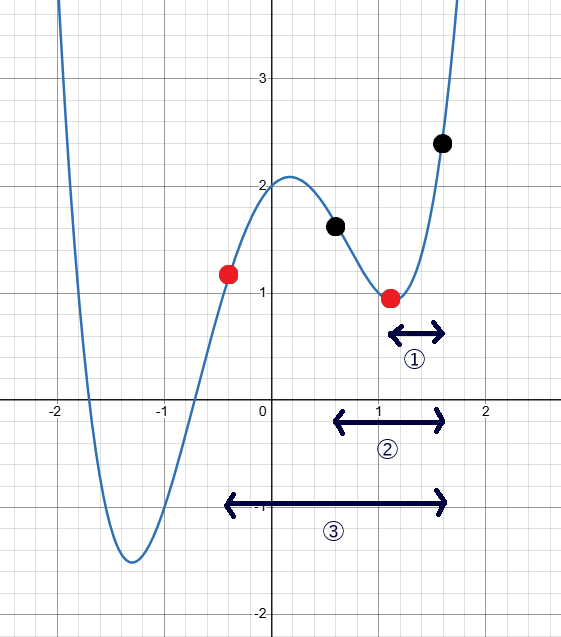
(基準は、局所最適解にはまってしまうときに取るものとして)➀が学習率をもともとの値の 半分 にしたとき、➁が学習率を変えなかったとき、➂が学習率の値を 倍 にしたときになります。
今回の場合だと、学習率が小さすぎたがゆえに局所最適解のトラップを越えられず、最小値にたどり着けなかったと考察することができます。
一方、一回目と二回目の値が次のグラフのようになっている場合についてはどうでしょうか?
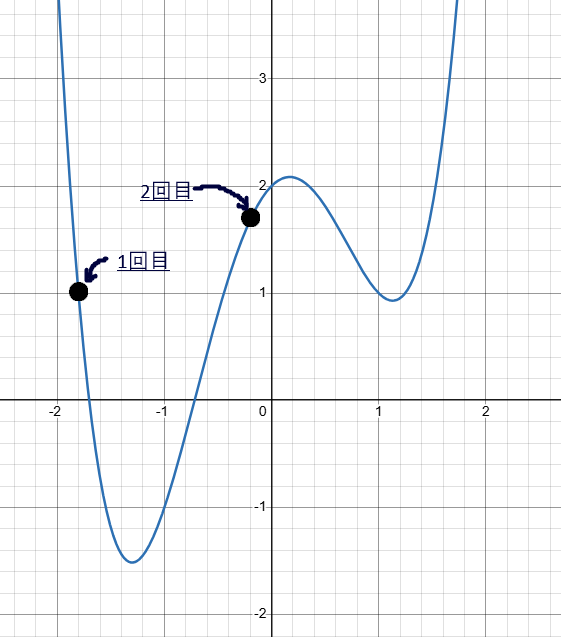
このグラフから、一回目に対しての学習率を 半分、 倍 にしたときのグラフは下のようになります。

先ほどと同じく、➀が学習率をもともとの値の 半分 にしたもの、➁が学習率の値を変えなかったとき、➂が学習率の値を 倍 にしたときに対応します。
今回のケースだと、むしろ学習率の値を大きくしてしまうと最小値を含むくぼみを飛び越えてしまうため、学習率の値は小さいほうが良いということになります。
このように、学習率の値は大きいから良い、小さいから良いと一概に言えるものではありません。また、学習率の値は大きくても小さくても対応できないケースが存在することが上の例からわかると思います。一つ目の例では、学習率が 半分 のときと 1倍 のときには最小値を含むくぼみにたどり着くことができず、二つ目の例では、学習率が 2倍 のときには最小値を含むくぼみにはたどり着けません。
SGDの問題点
SGD(stochastic gradient descent)とは、これまで扱ってきたような、パラメータの更新を以下の式で行うものになります。
しかし、この式でパラメータの更新をしてしまうことにはここまで紹介してきた局所最適解にはまってしまうものも含め幾つか問題点があります。ここでSGDの課題点を改めてまとめます。
1.局所最適解にはまってしまう問題
これは、先述のように、関数全体の最小値ではなくその付近の中での極小値にはまって抜け出せなくなってしまう問題です。
上の例でみたように、学習率の値を増加、あるいは減少させることで解決する場合もありますが、いかなる種類のくぼみにもはまらない学習率の値は存在しないため、このモデルは局所的な最適解に対して根本的な解決策を提供するものではないといえます。
2.勾配による学習効率が悪い問題
この問題を考えるには、変数が二次元以上である必要があります。下のグラフを見て下さい。
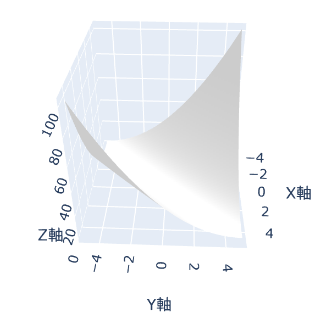
上の図に表された関数は、
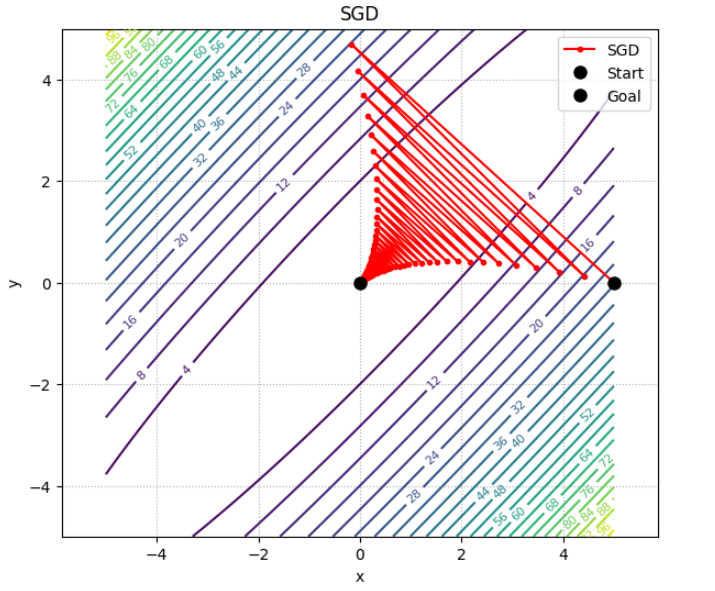
上の軌跡を見ればわかるように、斜め方向に余分に振動してしまっていることが分かります。これは、勾配の向きが最小値の値の方向に向いていない のが原因です。勾配の傾きを図示したものが下の図です。
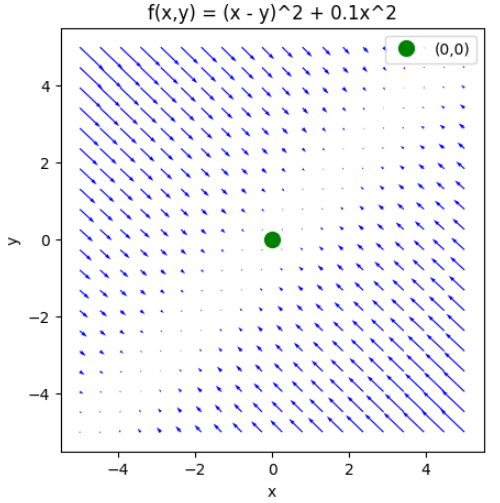
この図を見ればわかるように矢印の中のほとんどは最小値である緑色の点を向いていません。SGDでは、このようなケースにおいて非効率的な探索をしてしまうのです。
SGDの問題点の要点
これらのSGDの問題の原因は、まとめると 1つ前の傾きのみを基準にして更新の度合いを決定してしまうモデルだから と言えます。1つ前以前の値の傾向などを全て無視して、その場その場の勾配の傾きのみから判断を下してしまうので、長い目で見ると非効率的なことをしてしまうのです。
つまり、これらのSGDの問題点を解消するためには、値の更新の大きさに1回前の地点の情報だけでなく、2回前以前の情報も反映したものとすれば良いのです。この点を実践したグラフとして、Momentum 、 AdaGrad の二つを紹介します。
Momentum
Momentumは英語で運動量を表す用語です。その名の通り、このモデルでは、ボールが転がるのと同じような挙動をするように値の更新がされます。下の図を見ればボールが斜面を転がるように値が変わっていることが読み取れると思います。

ボールが転がるときには、小さい傾きであってもそれが一定区間続けば勢いが加算されるため、傾きが緩やかでも値の更新が遅くなりすぎるのを防ぐことができます。これは過去の一回の勾配だけではなく加算される速度の情報があって初めて可能になるものです。
Adagrad
このモデルは、値の変更の度合いを関数の形状に合わせて適応的に変更することで適切な大きさでパラメータを更新することを実現したモデルです。

上の図からだけでは、グラフの形状に対して適応的に値を更新していること以上のことを読み取ることは難しいですが、最初には一定の値だけあった「値の更新の度合い」を表すパラメータが、大きく動けば動くほど減らされる変更をされることで、始めの方は大きく値が変動し、徐々に動きが小さくなるように工夫されています。こちらの場合においても、一回前の勾配にとどまらない情報を持つハイパーパラメータを用意することで、値の更新が適切になされるように工夫されています。
モデルまとめ
ここまで、SGD、Momentum、AdaGradの三つのモデルの紹介をしてきました。この全てのモデルの値の変化を一つにまとめると下のようになります。
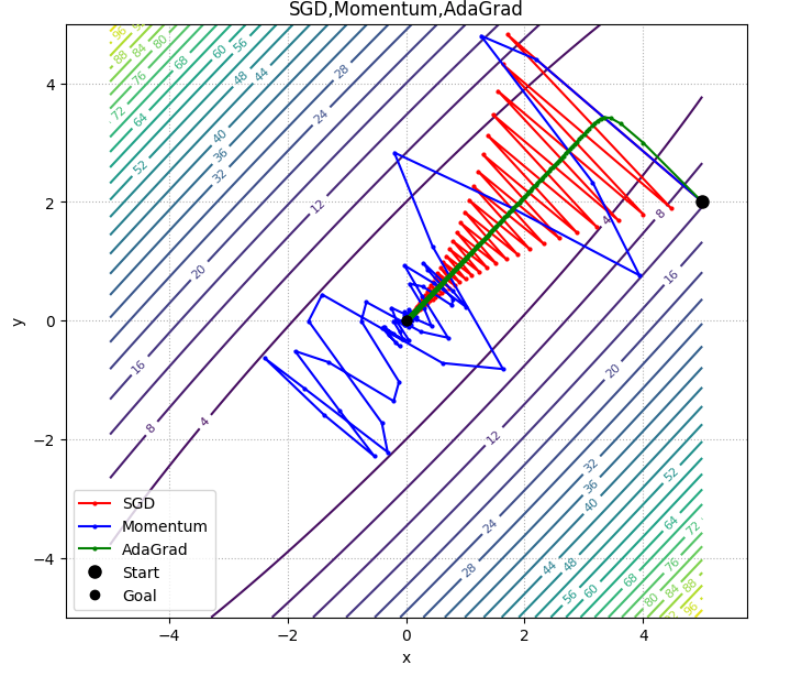
ここで注意をして欲しいのが、 どのモデルが優れていてどのモデルが劣っているという一般論は言えない ということです。グラフの形状に寄ってどのモデルが一番効率よくパラメータを更新できるかは変わってきます。
まとめ
今回の記事では、最小値に効率よくたどり着くために、パラメータの更新の工夫の仕方を説明しました。関数の形状を変える、損失関数の構造を変えるものとは異なり、そこにある損失関数に対していかに手際よく最小値にたどり着けるかを説明しました。これまで扱ってきたSGDの問題点を挙げ、MomentumやAdagradなどのモデルは過去一回のみにとどまらない値の参照を行うことでこの問題の解消を図っていることを理解できたと思います。
この記事は下の図のように体系化された記事の1つとして執筆されています。
対応するそれぞれの記事には下のトグルを開いて見たい記事をクリックすることで飛ぶことができます。
記事一覧
ニューラルネットワークの学習の全体像
A.訓練データとテストデータ、過学習
B.ミニバッチ学習
C.誤差逆伝播法
D.損失関数と勾配降下法
E.勾配消失問題
F.パラメータの更新
G.学習アルゴリズムの工夫
次の記事では、E.勾配消失問題 でも軽く扱いましたが、重みの初期値の決め方とBatch Normalizationについて解説します。閲覧するためには、下の記事をクリックしてください。
最後までご覧いただきありがとうございました!
Discussion