Zenn
🙆‍♀️

D.損失関数と勾配降下法

に公開
ディープラーニング
損失関数
勾配降下法
idea

この記事では、ニューラルネットワークの性能を評価する指標となる「損失関数」及び「活性化関数」を用いた最小値の求め方「勾配降下法」について解説します。

はじめに

前の記事（C.誤差逆伝播法）では勾配の求め方についての説明をしました。

https://zenn.dev/logeeeeee/articles/a5aa7a7a0b6c5f

この記事では誤差逆伝播法で求められた勾配値の扱い方を解説します。

この記事は、損失関数を用いて最小値を算出する一連の計算過程を解説した記事の中で、C.誤差逆伝播法に続く二番目の記事になります。

損失関数

損失関数は、そのモデルの認識精度の悪さを表す指標です。モデルから出力された値と実測値の差から計算されます。

損失関数の値は小さければ小さいほどモデルの性能は優れていることなるので、損失関数をより小さくする方法を探すのが目標になります。

損失関数の連続性、微分可能性

C.誤差逆伝播法の記事では、天下り的に理由の説明もなく微分の計算をしてしまいましたが、いったんこの微分計算を脇に置いて関数の最小値の求め方を確認してみることにします。

ニューラルネットワークの計算処理の過程の中で改変しうるのは「活性化関数」のみですが、出力値と実測値の間の誤差を計測する指標である「損失関数」も幾つかバリエーションがあります。つまり、「損失関数」の関数の形状を変えることができるものは活性化関数と損失関数の二つです。

このことを念頭において損失関数の最小値を求める方法を具体的な関数を使って考えてみましょう。実際には損失関数は多次元のグラフになることが多いですが、大きな次元の関数は直感的な理解が難しいので、ここでは便宜的に二次元のグラフで考えてみることにします。

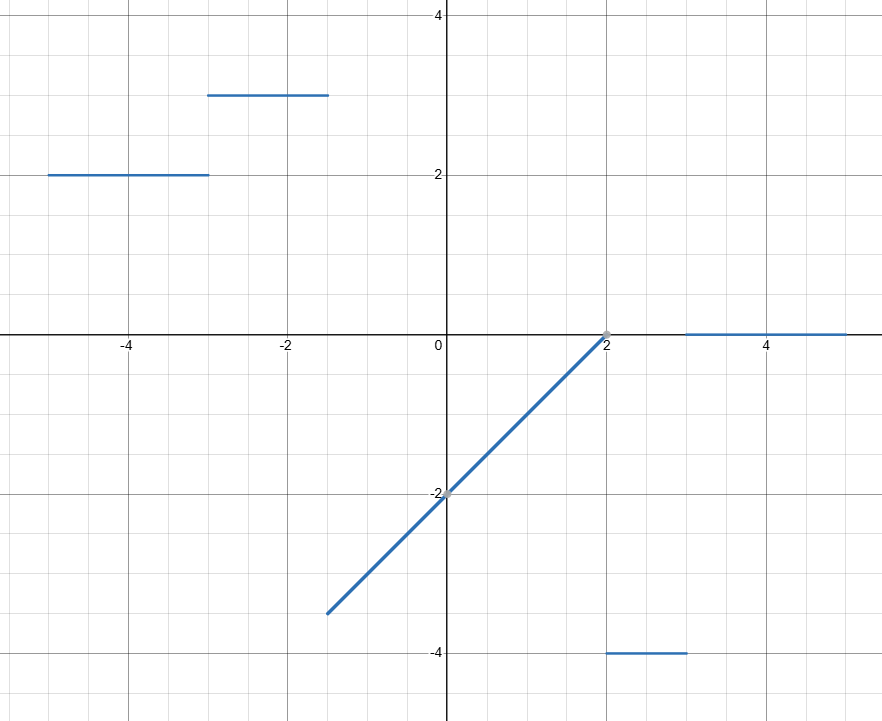
まず、-5 \le x \le 5 の区間で定義された非連続的な関数があるものとします。

f(x) = \begin{cases} 2 & (-5 \le x \le -3) \\ 3 & (-3 < x \le -1) \\ x-2 & (-1 < x \le 2) \\ -4 & (2 < x \le 3) \\ 0 & (3 \le x \le 5) \\ \end{cases}

このグラフは、y = -4 (2 < x \le 3)で最小値を取ります。しかし、コンピュータが計算をするときには目視で人間がしたように最小値を見つけ出すことはできません。ここで扱っている例は二次元の場合ですが、高次元のグラフほど目で見て最小値を見つけ出すことは難しくなります。

関数が非連続的であると分かっているときには、機械が最小値を見出す方法は、x = -2.1,2.0,-1.9　というように1つ1つの値に対する f(x) の値を取得する以外にありません。ある二地点の関数の値が分かっていたとしても、その二地点の間の値は全く違う関数によって定義されている可能性があるからです。

下の図のように幾つかの点の分布が分かっている場合でも...

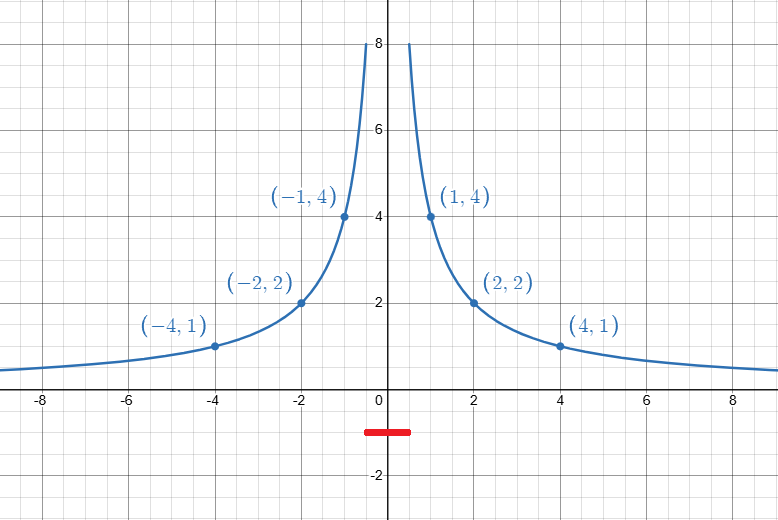
値を調べていない特定の区間(今回でいえば-0.5 \le x \le 0.5)は別の関数で定義されていることも起こりえてしまうのです。

損失関数の最小値を探索することは、関数が連続的で微分可能でないと困難になってしまうのです。

これは、活性化関数を工夫することで回避することができます。

ニューラルネットワークが入力から出力までに実行する計算処理は三段階に分けることができ、計算の内容で分類をすると、 1.結合している前のニューロンの重み付きの和を取る 、 2.活性化関数を通して値を変換する の二つに絞ることができます。ここで、1.の計算にニューラルネットワークが出力した関数の微分が不可能になるような変形は含まれないので、 2.活性化関数が微分可能であればよい ことになります。

こうすれば、微分可能な関数の合成関数でニューラルネットワークの出力は表されることになるので、あとは損失関数が微分不能でなければ問題ありません。

活性化関数を微分可能なものに変更することで、損失関数も微分可能になりました。

関数の最小値を求める方法

微分可能なグラフの最小値を求める一般的な方法は、その関数の導関数を求めて、導関数が0になる点の前後での導関数の符号の変化を調べることです。損失関数も、この方法で最小値を求めることは「理論的には」可能です。

しかし、この方法には大きな欠点があります。解析的に f(x) = 0 となるような方程式を解くことはf(x)が複雑になればなるほど難しくなってしまうのです。今回ここで紹介しているグラフは、便宜的に二次元に抑えてありますが、実際にはもっと高次のものとなってしまう上に、ニューラルネットワークの層が増えれば増える程、煩雑な関数が出力されることになってしまいます。ですが、ここで層の深さを抑えてしまうと、ニューラルネットワークの学習能力も下げてしまうことになります。

関数の複雑さに関わらず、その関数の最小値を発見するためにはどうすればいいでしょうか？

この問題を解決してくれる方法が、勾配降下法です。

勾配降下法

勾配降下法とは、 ある地点での勾配(二次元の関数なら微分値)を求めて、関数の値が減少する方向に向かって少しだけ移動する操作を繰り返すことで、より小さな値にたどり着こうとする手法 です。この手法を分解すると、次の2ステップに分けられます。



Step1 .今いる地点の座標や勾配などの情報を取得する。

Step2 . Step1で得た情報から、関数の値が小さくなる方向に変数の値を更新する。
このとき、傾きが急であればあるほど値の更新も大きくする。


言葉の説明ではイメージが湧きづらいので、具体的な関数y = \frac{1}{4}x^2を使って実験をしてみます。

勾配降下法の数値実験





　この関数のグラフは下のようになります。

f(x) = \tfrac{1}{4} x^2

今回はこのグラフに対して3回勾配降下法を実行することにします。

初期値は(4,4)とし、座標の更新は勾配の値を3倍した大きさとします。また、棒人間がいる場所は現在コンピュータがいる地点とします。

この関数の導関数は、y' = \tfrac{1}{4} \times 2x = \tfrac{1}{2}xとなります。

一回目の更新

Step1.まず、初期位置での勾配を計算してみると、y' = \tfrac{1}{2} \times 4 = 2です。

Step2.これを3倍した値の大きさ分、関数が減少する方向に更新するので更新されたx座標は
x = 4 - 2 \times 3 = -2です。

ニ回目の更新

初めのときとは違って今度は右肩下がりのグラフになっています。

Step1.この地点での勾配を計算してみると、y' = \tfrac{1}{2} \times (-2) = -1

Step2.次のx座標の値はx = -2 - (-1) \times 3 = 1です。

三回目の更新

二回目とは違って今度は緩やかな右肩上がりのグラフになっています。

Step1.この地点での勾配を計算してみると、y' = \tfrac{1}{2} \times 1 = \tfrac{1}{2} です。

Step2.よって次のx座標の値はx = 1 - \tfrac{1}{2} \times 3 = -\tfrac{1}{2}です。

最終結果

最終的に到達した座標は(-\tfrac{1}{2},\tfrac{1}{4})です。

初期値から三回目に座標を更新した後までの点の軌跡は下のグラフのようになります。

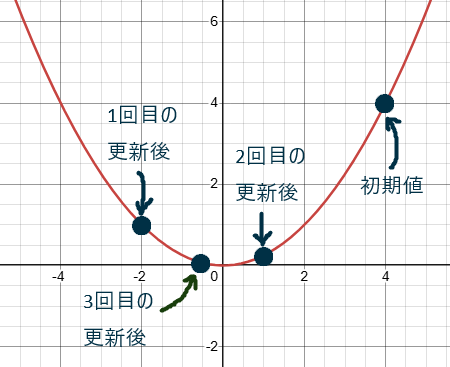
この実験を通して分かるように、勾配降下法を使えば谷底の近辺を行ったり来たりしながら谷底に近づくことができます。微分可能な関数であれば、今いる地点の座標の傾きの値を用いて座標を何度も更新することで、だんだんと関数の値が小さな値に更新されていく様子が直感的に理解できたのではないでしょうか？

勾配の計算には誤差逆伝播法を使用しているため、深い層をもつニューラルネットワークであっても勾配の計算は効率良く実行することができます。勾配降下法の強みは、損失関数が複雑な関数であっても勾配さえ分かればより小さな値を探索できることにあります。

最後に

この記事では、勾配降下法の手法について解説しました。勾配降下法は関数が複雑でも誤差逆伝播法で算出された勾配が分かればより小さい値を探し出すことができる優れものです。

この記事は下の図のように体系化された記事の1つとして執筆されています。

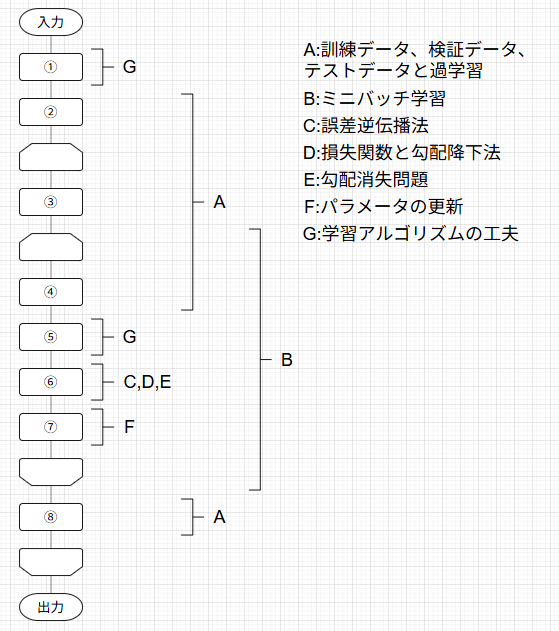
対応するそれぞれの記事には下のトグルを開いて見たい記事をクリックすることで飛ぶことができます。

記事一覧

ニューラルネットワークの学習の全体像
https://zenn.dev/logeeeeee/articles/a3119f68fa261c

A.訓練データとテストデータ、過学習
https://zenn.dev/logeeeeee/articles/78d1a686f4397d

B.ミニバッチ学習
https://zenn.dev/logeeeeee/articles/ca5c607197d183

C.誤差逆伝播法
https://zenn.dev/logeeeeee/articles/a5aa7a7a0b6c5f

D.損失関数と勾配降下法
https://zenn.dev/logeeeeee/articles/b972b5bb03c173

E.勾配消失問題
https://zenn.dev/logeeeeee/articles/6d8784473faaf2

F.パラメータの更新
https://zenn.dev/logeeeeee/articles/e89c1cc09008ed

G.学習アルゴリズムの工夫
https://zenn.dev/logeeeeee/articles/b7a4798fac2a2b

次の記事では、勾配降下法が陥りうる問題の1つ「勾配消失問題」について説明しています。

https://zenn.dev/logeeeeee/articles/6d8784473faaf2

最後までご覧いただきありがとうございました！

Discussion