C.誤差逆伝播法
この記事では、 勾配降下法 を実行するにあたり必要となる勾配を算出する方法 誤差逆伝播法 を解説しています。
はじめに
1つ前の記事ではミニバッチ学習などの訓練データの分割方法について解説しました。
深層学習において、効率的に関数の最小値を求めるためには「勾配降下法」を使うことになりますが、そのためには関数の勾配を求める必要があります。関数の勾配とは、簡単にいうと微分の対象を、一変数関数から多変数関数に変えたものとなります。一般的に使われる

この記事は、損失関数を用いて最小値を算出する一連の計算過程を解説した記事の中の最初の部分になります。
そもそも勾配とは?
そもそも勾配とは何でしょうか?上の説明では、ある種の微分といいましたが、多変数のグラフの1つの二変数関数は、下の図のように曲面を表すものです。

そのため、ある一つの点を通る微分と言っても向きによって無限通りの傾きが求められてしまうことになります。 下の図は(x,y) = (0,2)を通る曲線のうち、x軸に平行な方向とy軸に平行な方向の矢印を図示したものです。

勾配 は、この無限通りある方向のうち、最も関数の減りが大きい方向 の傾きの値になります。

また勾配は、x成分とy成分についてそれぞれの 偏微分 をした結果を足し合わせると得られます。偏微分についてはここでは詳しくは解説しませんが、要はx成分方向のみ、y成分方向のみに絞って微分を行ったものだと考えて下さい。
次に、この勾配を求めるために使われる 微分 の計算方法について説明します。
数値微分と解析微分
ここでは、
微分とは、下の数式のように定義される計算のことです。limの記号は、矢印の起点の変数の値を限りなく矢印の先の値に近づけることを表します。
この計算式には、hの値が0に限りなく近づいていく、極限 の計算が含まれています。このような数学的な定義に従った計算の仕方を 解析微分 と呼びます。それに対して、極限を取らずにhを有限な微小量で置き換えて計算をしたものを 数値微分 と呼びます。仮に、h = 0.0001とすると数値微分の計算は下のように書き換えられます。
左辺と右辺を繋いでいる二本の波線は「ほぼ等しい」ことを表しています。厳密には、右辺は微分の定義式に従っていないので両辺の間に等式が成り立つわけではありませんが、それでも十分小さなhの値を使えばおおよそ正しい値が得られるのは分かると思います。
数値微分は、実装は簡単でありながらも計算に時間がかかるという欠点も持ち合わせています。
誤差逆伝播法
誤差逆伝播法とは、簡単にいうとニューラルネットワーク用に開発された微分の計算方法です。ニューラルネットワークは、その構造上、前の入力層から順に微分計算をしていくと計算量が非常に多くなってしまうため、それを避けるために後ろの層から遡りながら計算をすることからこのような名前が付けられました。この方法は、厳密に正しい値を計算するものなので、解析微分の方法の一つに分類されます。
勾配確認
しかし、正確に且つスピーディに微分の値を算出できる誤差逆伝播法にも1つ問題点があります。計算が複雑で実装の途中でミスをしやすいのです。せっかく正確に計算できる方法を使ったとしても、計算それ自体が間違っていたら元も子もありません。
数値微分は、実際の微分計算で使うには性能的に少し足りないものの、その実装の簡単さから誤差逆伝播法の計算結果が正しいものであることを確認するために使われることがあります。
誤差逆伝播法の結果を数値微分の結果と照らし合わせて計算の正しさを保証することを、 勾配確認 といいます。
まとめ
今回の記事では勾配降下法の計算に必要不可欠である誤差逆伝播法について解説しました。これで、勾配降下法をするための下準備が整いました。
この記事は下の図のように体系化された記事の1つとして執筆されています。
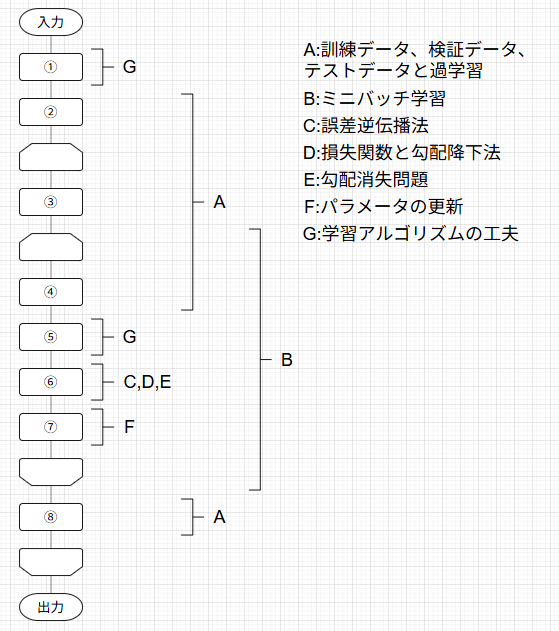
対応するそれぞれの記事には下のトグルを開いて見たい記事をクリックすることで飛ぶことができます。
記事一覧
ニューラルネットワークの学習の全体像
A.訓練データとテストデータ、過学習
B.ミニバッチ学習
C.誤差逆伝播法
D.損失関数と勾配降下法
E.勾配消失問題
F.パラメータの更新
G.学習アルゴリズムの工夫
次の記事ではいよいよ 勾配降下法と、その計算を実行する対象となる 損失関数 について解説します。
最後までご覧いただきありがとうございました!
Discussion