G.学習アルゴリズムの工夫
この記事では、重みパラメータの初期値やデータの整形をするBatch Normalizationの働きを解説しています。
はじめに
これまでの記事では、ニューラルネットワークの学習の内部構造について解説してきました。1つ前の記事に飛ぶには下のブックマークをクリックしてください。
今記事では、ニューラルネットワークという処理体系の内容ではなく、そこに入れる入力値の決め方についての工夫の仕方を取り扱っています。処理される前にパラメータなどを整形することは一見、ニューラルネットワークの学習を少し改善するぐらいの効果しか持たないように思えますが、実際にはこれが正しく設定されていないと学習が最悪失敗に終わってしまうことがあるくらい重要なものです。この種のデータの整形は、学習が正しく行われることを保障するのには必ず考慮しなければならないものです。
この記事では、学習アルゴリズムの工夫の仕方として大きく次の二つのテーマを取り上げます。
1.重みパラメータの初期値を正しく決めること
2.データの値の正則化を行うこと(Batch Normalization)
この記事の本題に入る前に、そもそもなぜこれが正しく決められなければいけないのかを遡ってみていくことにします。
そもそも学習とは何か?
ニューラルネットワークにおける学習とは、簡単にまとめると次のようにまとめられます。
「与えられた入力に対して適切な出力を返せるように、ネットワーク内部のパラメータを調整すること」
これは、例えば犬と猫のどちらかの画像が与えられたときに、犬が入力として与えられた場合には「犬」と出力し、猫が入力として与えられたときには「猫」と出力を返せるようにニューラルネットワーク内部で重みやバイアスを調整するということです。言い換えれば、異なる入力が与えられたときには異なるものとして識別できるようになることが学習であり、入力情報に基づいた的確な差別化ができるようになることが効率的な学習ができるか否かの分け目となるのです。このことが重みパラメータやデータの値の整備をすべき根幹の理由になります。
1.重みパラメータの初期値を正しく決めること
重みパラメータは、設定する値が大きすぎても小さすぎても安定した学習をすることができなくなってしまいます。ランダムな初期値で学習を始めてしまうと、勾配消失や勾配爆発といった問題が起きてしまうことに繋がりかねないからです。
初期値の定め形は、活性化関数の種類に応じて2種類あります。
Xavierの初期値
この初期値は、そのノードに至るまでに経由したノードの個数をn個とするとき、そのノードの重みパラメータの分散が
1.活性化関数の勾配が大きい領域に固まった分布となる
2.データ同士の差別化をするのに適切な幅をもつ分布となる
という二つの条件を満たす確率を上げることができます。言い換えれば、入力の値の差を出力の値の差として反映できるような分布になっていると言えます。
この重みパラメータの初期化の操作は、活性化関数が線形であることを前提として導かれたものです。(実際の活性化関数に線形関数は使えませんが)ですので、 シグモイド関数 やtanh関数 など出力が正負対称な活性化関数に使われることになります。
Heの初期値
こちらは、活性化関数が線形関数であることを前提として作られたXavierの初期値を、ReLU関数でも使えるように改良したものです。ReLU関数では、入力の値が負のときには入力される値に関わらず0を出力し、値の分散は正の部分の半分になってしまうため、それを補うように分散が
Heの初期値が使用される対象は、ReLU関数 や ReLU関数の派生関数 です。
Batch Normalization
Batch Normalizationは、データそのものの分散を調整すれば学習を効率的にできるという発想から生まれた手法になります。Batch Normalizationの名前の通り、バッチごとに値を正規化するものです。
これを実行することで得られる恩恵は多岐にわたります。主なものをリスト形式でまとめます。
- 重みの初期値に影響をあまり受けない安定した学習ができる
- 学習率が大きくなっても損失が発散しないため、学習係数を大きくすることができ、学習を効率的に行うことができる
- 活性化関数を通る前に分布を正規化するため、勾配消失問題を起こしにくくすることができる
- ミニバッチごとに調整を加えるため、学習ステップで適度にノイズが入り込み、過学習が防止できる
これらの恩恵が受けられるようになったことで、ニューラルネットワークの層をより深くすることが可能になり、ニューラルネットワークの学習力を向上させる貢献を果たしました。
最後に
この記事では、学習をより安定的に且つ効率的に実行するため、重みパラメータの値の調整にXavierやHeの初期値を使うべきことと、バッチごとにデータの分布を正規化するBatch Normalizationの層を挟むべきことを説明しました。
この記事は下の図のように体系化された記事の1つとして執筆されています。
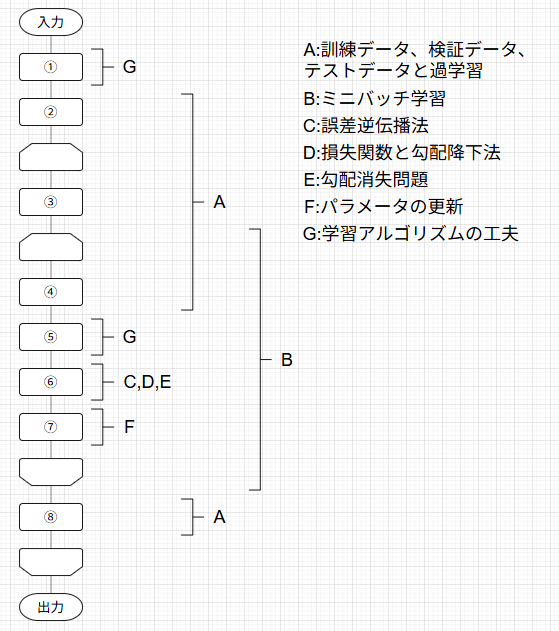
対応するそれぞれの記事には下のトグルを開いて見たい記事をクリックすることで飛ぶことができます。
記事一覧
ニューラルネットワークの学習の全体像
A.訓練データとテストデータ、過学習
B.ミニバッチ学習
C.誤差逆伝播法
D.損失関数と勾配降下法
E.勾配消失問題
F.パラメータの更新
G.学習アルゴリズムの工夫
この記事で「ニューラルネットワークの学習」の内容の解説が全て終わりました。
最後まで読んでいただき、本当にありがとうございました!
Discussion