B.ミニバッチ学習
この記事では、ニューラルネットワークの学習において、一度の学習に使われるデータ量に関する内容を取り扱っています。
はじめに
1つ前の記事(A.訓練データ、検証データ、テストデータと過学習)では、データを幾つかに分けた上で学習を実行すべき理由を説明しました。下のurlから一つ前の記事に飛べます。
ミニバッチ学習の説明にいきなり入る前に、まずデータ量に関する用語をまとめます。
データに関する用語のまとめ
データの量を表す用語のまとめです。
データの分割の行程も含めてデータの分割の仕方を図示します。下の図では検証データは1つのバッチごとに使われるものとしています。

それぞれの用語、そしてデータの変形のされ方のおおよそのイメージは掴めたでしょうか?
ここからは「エポック」の内部構造について見ていくことにします。
訓練データの総数、バッチサイズ、イテレーション数の間に成り立つ関係式を先に紹介します。この式は、主にイテレーション数を求めたいときに使われます。
一度に投入するデータ量による分類
データに関する用語の図示に用いた図では、一度に投入されるデータ数は訓練データ全体を幾つかに等分割したもののうちの1つとなっていますが、これは固定ではありません。一度に投入するデータ量は一つずつでもよく、一遍に全て投入してもよいのです。
オンライン学習
オンライン学習で一度に投入するデータの個数は1個です。これは一度に投入するデータ量としては最少です。この場合には、実行するイテレーション数は訓練データの総数と一致します。
下図はこの学習方法のイメージ図です。

バッチ学習(オフライン学習)
オンライン学習が一度に1つずつのデータを投入してイテレーションを回したのに対し、バッチ学習では一回で全てのデータを投入します。バッチ学習はオンライン学習と反対のものとして、オフライン学習と呼ばれることもあります。次の二つの等式が成り立ちます。
下図はこの学習方法のイメージ図です。

ミニバッチ学習
ミニバッチ学習は、訓練データを小分けにしながらデータを投入する方法にです。ミニバッチ学習のバッチサイズはコードの実行者が自由に決められるハイパーパラメータとなります。
下図はこの学習方法のイメージ図です。

一回の学習に用いるデータばランダムに抽出されるため、1つ1つのミニバッチのデータ数が少なすぎなければこのデータの塊(これのことをミニバッチと呼びます)は全体のデータの傾向とおおよそ一致します。
具体的な値を使った計算
一度に投入するデータ量に関しても、言葉のみで構成された式を使うよりも具体的な値を使用した計算をする方がイメージが掴みやすいと思います。
例として、全データ数が80,000個ある場合を考えてみます。
データの分割
まず、最初にデータを訓練データ、検証データ、テストデータを分割します。今回は次のように分けます。データの分割は、全体の行程の中で一度だけするものです。エポック数を増やしてもここの分割が何度もされることはありません。
ここからイテレーションを回すにあたって一回のイテレーションに使用するデータ量を決めます。
オンライン学習
オンライン学習は、バッチサイズが1(個)であることを説明しました。よって、イテレーション数は
バッチ学習
バッチ学習は、一度に全てのデータを使用する方法なので、今回の場合だと
ミニバッチ学習
ミニバッチ学習は、幾つかのデータのまとまりを一回のイテレーションで使用する学習手法です。この学習手法では、特にバッチサイズとイテレーション数に指定はありません。バッチサイズは、1(個)より多く、訓練データの総数より少なければ自由に定めることができます。
今回はバッチサイズが 100(個),200(個),600(個)の場合について考えてみることにします。
1.(バッチサイズ) = 100(個)
このときのイテレーション数は、
2.(バッチサイズ) = 200(個)
このときのイテレーション数は、
3.(バッチサイズ) = 600(個)
このときのイテレーション数は、
バッチサイズとイテレーション数のまとめ
ここまで扱ってきた全てのケースを表にまとめました。
訓練データの総数が60000個のとき
| 学習の手法の名称 | オンライン学習 | ミニバッチ学習1 | ミニバッチ学習2 | ミニバッチ学習3 | バッチ学習 |
|---|---|---|---|---|---|
| バッチサイズ(個) | 1 | 100 | 200 | 600 | 60,000 |
| イテレーション数(回) | 60,000 | 600 | 300 | 100 | 1 |
エポック
全てのミニバッチを一度ずつ学習しただけでは、学習の精度はまだ十分とはいえません。数量の限られたデータのみを使ってパラメータが最適な値を取るようにするためには、訓練データをシャッフルした上で何度かエポックを回す必要があります。
最後に
この記事では、ニューラルネットワークの学習において欠かすことのできないデータの扱い方、特に訓練データを学習に用いる際の扱い方について解説しました。
この記事は下の図のように体系化された記事の1つとして執筆されています。
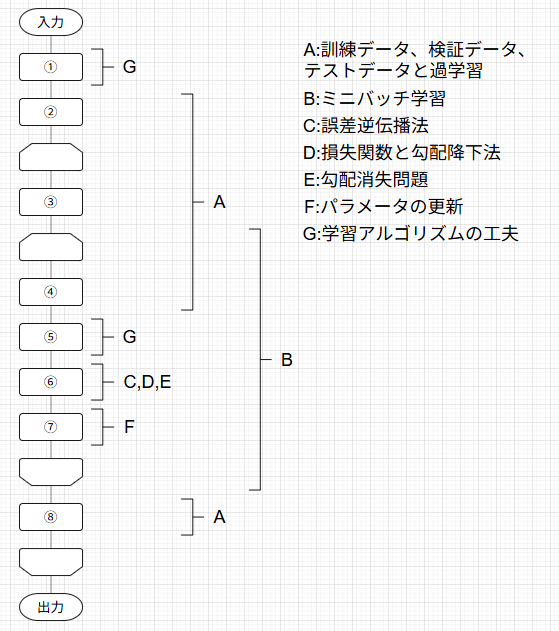
対応するそれぞれの記事には下のトグルを開いて見たい記事をクリックすることで飛ぶことができます。
記事一覧
ニューラルネットワークの学習の全体像
A.訓練データとテストデータ、過学習
B.ミニバッチ学習
C.誤差逆伝播法
D.損失関数と勾配降下法
E.勾配消失問題
F.パラメータの更新
G.学習アルゴリズムの工夫
今回扱った内容は、学習をしてパラメータの更新をするというループ全体の構造に関するものでした。次の記事C.誤差逆伝播法では、いよいよ深層学習の中身についての解説に入ります。
最後までご覧いただきありがとうございました!
Discussion