E.勾配消失問題
この記事では、実際に勾配降下法を用いて最小値を求めようとするときに陥りうる問題である 勾配消失問題 とその解決方法について説明します。
はじめに
この記事の内容は、C.誤差逆伝播法、D.損失関数と勾配降下法に引き続いて、損失関数を用いて最小値を求めるアルゴリズムについて扱っています。一つ前の記事へは下のブックマークから飛ぶことができます。
勾配降下法が陥り得る問題である勾配消失問題を解消する形でこのアルゴリズムの修正をします。
勾配降下法で起こり得る事態
D.損失関数と勾配降下法に引き続いて、機械目線の関数の中のパラメータの更新を考えてみます。次の例は勾配降下法を用いているときに起こり得る事態の一例です。こちらは二回だけ考えてみます。ここでの回数は初期値から座標を更新した回数である必要はありません。何百回か値を更新した後にカウントし始めた一回目、二回目であったとしても性質上の違いはありません。
一回目の更新
Step1.勾配の値は、今回の場合ではほぼ0です。
Step2.Step1で求めた勾配の値が非常に小さいので、変数の値の更新もほとんどありません。
二回目の更新

Step1.勾配は、相変わらずほぼ0です。
Step2.Step1で求めた勾配の値が非常に小さいので、今回の変数の値の更新もほとんどありません。
勾配消失問題
D.勾配降下法で用いている更新のモデルでは、勾配降下法の関数の値は一度平らになってしまうとそこから先はほとんど更新されなくなります。上のようなほとんど動かない状態に到達したときには関数の最小値にたどり着くことができたと断言できるでしょうか?
実は、必ずしもそうは言えません。下のグラフの 1 <= x <= 3 の部分のように最小値でなくてもグラフの傾きが0にほぼ等しい部分はあり得るからです。

グラフの傾きが0に近い部分では勾配降下法による値の更新がストップしてしまうため、最小値以外で勾配が0付近になる部分はできる限り生じないようにしなければならないのです。
勾配消失問題の解決策
勾配消失問題は、ニューラルネットワークの層が深くなるほど起こりやすくなってしまう問題です。勾配消失問題の解決方法は様々ありますがこれは大きく1.構造を改変するアプローチと2.構造を改変しないアプローチの二つに分けられます。
前者は「活性化関数」と「損失関数」の組み合わせが適切になるように調整して構造を整えることにあたります。また、後者にあたるものとして重みの初期値を工夫する、正則化を行う、学習率を調整することの三つを紹介します。
1.構造を改変するアプローチ ー「活性化関数」と「損失関数」を適切に調整する。
活性化関数が「ロジスティック関数」で損失関数が「誤差二乗和」のときには勾配消失問題に直面することになります。この組み合わせでは、シグモイド関数の変数の値が小さいときや大きいときには傾きが0に近づいてしまう影響が、誤差二乗和では緩和できないのが原因です。
そのため、この問題の解決のアプローチとしては、
(1)活性化関数が勾配消失問題を回避できるようなものに変更する
(2)損失関数を活性化関数にフィットしたものに変える。
の二通りがあることになります。
(1)活性化関数が勾配消失問題を回避できるようなものに変更する
シグモイド関数は導関数の値が0に近づいてしまう領域があり、これが勾配消失問題の原因です。つまり、シグモイド関数ほど傾きが0に近づく領域が広範にわたらない関数であれば勾配消失問題は解決することができます。
そうなると、まず検討してみたくなるのが恒等関数となりますが、この関数は線形関数であり、ニューラルネットワークの学習力を損なってしまうため、採用することはできません。そこで x < 0 の領域では勾配が0になってしまうものの、非線形関数であるReLU関数を使うことを考えてみましょう。この場合、正の領域では勾配消失問題を回避できており、シグモイド関数と比較して導関数がかなり大きい値を取り続けているので大丈夫そうです。負の領域で傾きが0になっていることは正の領域で傾きが0になることに比較すると大した問題ではないので、一応問題はクリアできたといえます。
(2)損失関数を活性化関数にフィットしたものに変える。
今度は損失関数を変更する選択肢を考えます。この場合、シグモイド関数の傾きが小さくなる x < 0 や 1 < x の領域でそれを補うような傾きを持つ損失関数を使えばよいことになります。実際、「交差エントロピー誤差」はうまくこれを打ち消す効果を持つので、「シグモイド関数」と「交差エントロピー誤差」の組み合わせは全体として勾配消失を起こしません。
2.構造を改変しないアプローチ
(1)重みの初期値を工夫する。
これは重みの初期値をデフォルトの値のままニューラルネットワークに通すのではなく、適切な範囲に収まるようなものに変更してから通すことで勾配消失を起こす領域に分布をしないようにする調整です。ですが、この調整は根本から勾配消失問題の解消を図る類のものではないため、何層か経た後に勾配消失がある領域にはまってしまう問題を構造的に防ぐことはできません。
初期値については、「G.学習の効率化」でより詳しく説明しています。
(2)正規化を行う。
これは2015年に発表された比較的新しい手法です。代表的なアルゴリズムはBatch Normalizationと呼ばれます。ミニバッチごとにデータの分布を正規化するため、活性化関数の中で勾配が小さくない部分に集中的に値を通すことができます。
Batch Normalizationについては、「G.学習の効率化」でより詳しく説明しています。
(3)学習率を調整する。
学習率をグラフの形状に応じて適応的に最適化するアルゴリズムは、勾配の大きさの調整を行うことで勾配消失問題に対処することができます。
学習率については、詳しくは F.パラメータの更新 で説明します。
最後に
この記事では、勾配降下法を使っている最中に陥り得る問題の1つ「勾配消失問題」を説明し、これの解消の仕方を多角的に紹介しました。
この記事は下の図のように体系化された記事の1つとして執筆されています。
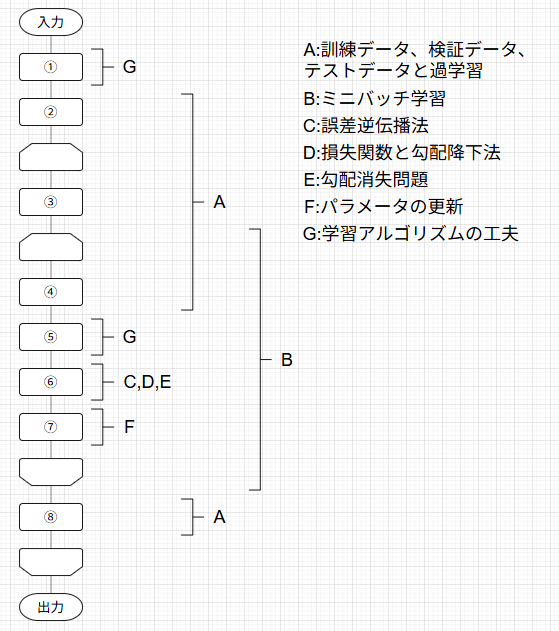
対応するそれぞれの記事には下のトグルを開いて見たい記事をクリックすることで飛ぶことができます。
記事一覧
ニューラルネットワークの学習の全体像
A.訓練データとテストデータ、過学習
B.ミニバッチ学習
C.誤差逆伝播法
D.損失関数と勾配降下法
E.勾配消失問題
F.パラメータの更新
G.学習アルゴリズムの工夫
次の記事では、勾配降下法の別の問題として「局所最適解にトラップされる問題」や「値の更新が効率的でない問題」を取り上げます。そして、ここまで扱ってきた勾配降下法のモデルとは他のパラメータの更新方法を検討することでこれの解決の糸口とすることができることを説明しています。
最後までご覧いただきありがとうございました!
Discussion