📊

ケーススタディ：キャンペーン施策の効果測定｜独立2群の差

に公開
マーケティング
データ分析
統計
ビジネス
効果検証
tech

はじめに

教育やマーケティングの現場では、“施策の効果検証”が求められる場面が多くあります。
この記事では、UCIの「Bank Marketing Data Set」を用いてキャンペーン施策の効果を統計的に検証するプロセスを紹介します。

分析目的

マーケティング施策の成果（y = yes か no）によって、
キャンペーンにおける連絡回数（campaign）に差があるかを検定し、
顧客の反応と接触頻度の関係を統計的に確認

使用データ

  • データセット：Bank Marketing Data Set（UCI Machine Learning Repository）
  • ポルトガルの銀行によるダイレクトマーケティング（電話営業）キャンペーンの記録
  • サンプル数：45,211件
  • 使用変数：
    • campaign：最後のマーケティングキャンペーンでの通話回数
    • y：定期預金の申し込み有無：yes / no（施策成果）

使用手法

分析ステップ

ステップ1：データの基礎俯瞰

  • 欠損値：
    • campaign：なし
    • y：なし
  • データ型：
    • campaign：int
    • y：object
  • 各変数の分布
    • campaign：最小値：1　最大値：63

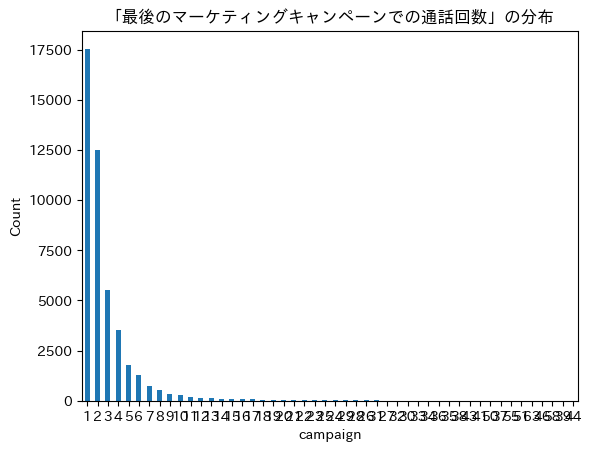
      右裾が長い形となっており、基本的に数回の通話が多いが、
      最大値が63と極端に多く通話しているケースも見られる

    • y：yes件数：5,289　no件数：39,922

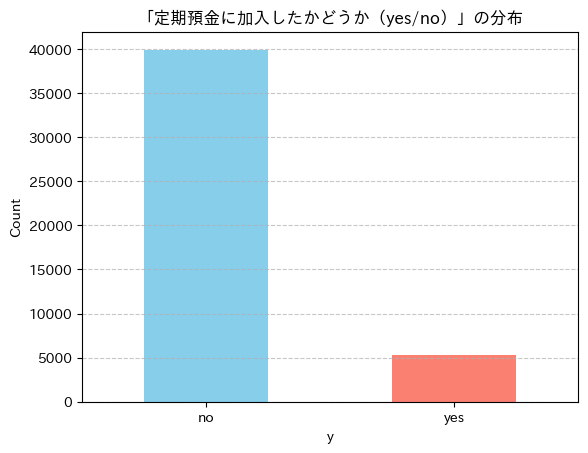
      noがyesの約8倍と圧倒的に多い

  • ヒストグラム

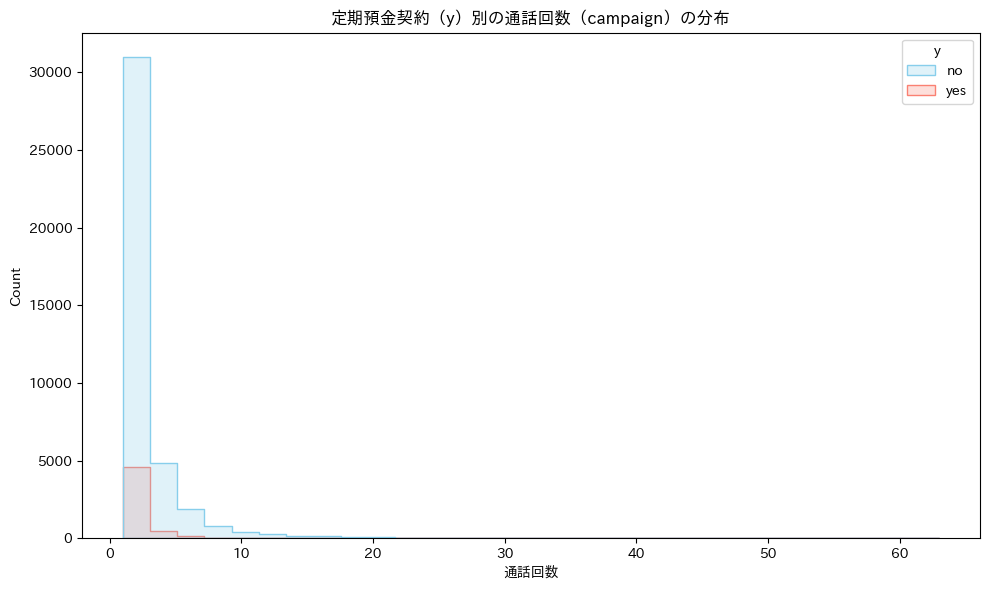
    分布の形自体は似ているが、noの件数のほうが多いため、このような結果になっていると推測

  • 箱ひげ図

    noのほうが外れ値の幅が多いという違いはあるが、最大値部分より下は違いが見えない印象

ステップ2：正規性の確認

独立2群の差検定を実施するにあたって前提となる「正規性」を確認。
n>5000なのでShapiro-Wilkは使用せず、Anderson-Darling検定とQ-Qプロット、
ヒストグラムで確認する。　※ 使い分けガイド

  • Anderson-Darling検定　→ 手法の説明はこちら
    • yesグループ
      • AD検定統計量：561.765
      • 設定有意水準：0.05　臨界値：0.786
      • 帰無仮説：棄却できない
      • 解釈：正規分布に従うとみなせる（厳密には「従わないといえない」）
    • noグループ
      • AD検定統計量：4610.447
      • 設定有意水準：0.05　臨界値：0.787
      • 帰無仮説：棄却できない
      • 解釈：正規分布に従うとみなせる（厳密には「従わないといえない」）
  • Q-Qプロット
    • yesグループ

    中央付近（0付近）は点が赤線にほぼ沿っている → 中央の分布は正規分布と近い形
    両端が理想線(赤線)から大きく逸れている → 外れ値が多い可能性がある

    • noグループ

    yesグループと同様の傾向がみられる

  • ヒストグラム
    • yesグループ

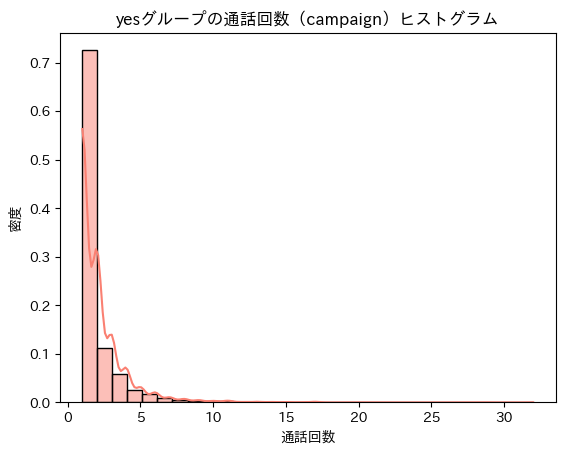
    ベル型ではなく右に長く伸びた形をしているため、正規分布ではないと解釈
    ※サンプルサイズに依存せず分布の形を見るために縦軸を「密度」で表示

    • noグループ

    yesグループと同様の形をしているためこちらも正規分布ではないと解釈

ステップ3：等分散性の確認

「正規性」と同様に、独立2群の差検定を実施するにあたって前提となる「等分散性」を確認。
「正規性」が怪しいため、正規性が不要なLevene検定・Brown-Forsythe検定・Frigner-Killeen検定を検討。

  • Levene検定　→ 手法の説明はこちら
    • 検定統計量：337.612　p値：3.97e-75
    • 設定有意水準：0.05（両側検定）
    • 帰無仮説：棄却
    • 解釈：等分散ではない
  • Brown-Forsythe検定　→ 手法の説明はこちら
    • 検定統計量：142.560　p値：8.22e-33
    • 設定有意水準：0.05（両側検定）
    • 帰無仮説：棄却
    • 解釈：等分散ではない
  • Frigner-Killeen検定　→ 手法の説明はこちら
    • 検定統計量：133.841　p値：5.92e-31
    • 設定有意水準：0.05（両側検定）
    • 帰無仮説：棄却
    • 解釈：等分散ではない

    いずれの手法でも等分散性がみられなかった（＝yesとnoグループでばらつきの程度が異なる）
    ステップ1の箱ひげ図でも外れ値の程度が違ったので納得できる結果となっている

ステップ4：独立2群の差検定 実施

前提である「正規性は微妙」「等分散性はなし」という結果から、Welchのt検定とMann-Whitney検定の両方で評価

  • Welchのt検定　　　 → 手法の説明はこちら

    • t値：-22.801　p値：3.73e-112
    • 設定有意水準：0.05(両側検定)
    • 帰無仮説：棄却
    • 解釈：yesとnoグループで有意な差がある

  • Mann-Whitney検定 → 手法の説明はこちら

    • U値：90300543.500　p値：1.95e-71
    • 設定有意水準：0.05(両側検定)
    • 帰無仮説：棄却
    • 解釈：yesとnoグループで有意な差がある

示唆と次のアクション

  • 分析結果：yesとnoグループで有意な差がみられた
  • 今回の示唆：
    キャンペーン中の通話回数が定期預金の申し込み有無に対して影響を与えた可能性がある

    外れ値の幅が異なるが、中央値で比較するMann-Whitney検定においても有意差がみられたため
    外れ値を除いても有意差があると解釈できる

  • Next分析案：
    • 外れ値を除いたうえで再度検証

      今回ケースは外れ値の幅が異なっているために有意な差がみられていると推測
      しかし、極端な通話回数は現実的な運用としては適切でないため、
      外れ値を除いた検証も検討したほうが良いと考える

    • campaign回数別契約率の傾向確認

      最適な接触回数帯の特定につながる（例：4回目までが効果大など）

    • 顧客セグメント別の分析

      よりパーソナライズされたマーケ施策への足掛かりとなる

  • ビジネスアクション案
    • 適切な「接触回数」の設定
    • 通話回数が極端に多いケース（例：15回以上）を精査し、対応の見直しを検討
    • 少ない回数で契約に至った顧客の特徴を確認し効率的なターゲティングを実現

補足リンク・参考情報

Discussion