📊

ケーススタディ：学習効果の評価｜対応のある2群の差

に公開
データ分析
統計
ビジネス
効果検証
統計的検定
tech

はじめに

教育やマーケティングの現場では、“施策の効果検証”が求められる場面が多くあります。
この記事では、UCIの「Student Performance Data Set」を用いて学習前後の成績変化を分析し、施策の効果を統計的に検証するプロセスを紹介します。

分析目的

1年間のG1（1回目の成績）とG3（最終成績）の成績に有意な差があるか検定し、
学習の効果を統計的に確認する

使用データ

  • データセット：Student Performance Data Set（UCI Machine Learning Repository）
  • ポルトガル語の授業を受けた学生
  • サンプル数：649ペア
  • 変数：
    • G1：1回目の成績（施策前）
    • G3：最終成績（施策後）

使用手法

分析ステップ

ステップ1：データの基礎俯瞰

  • 欠損値：なし
  • データ型：int
  • ヒストグラム

    G1とG3でぱっと見は似てるが、G3のほうが高い点の人が多く、0点近くの件数も多い

  • 箱ひげ図

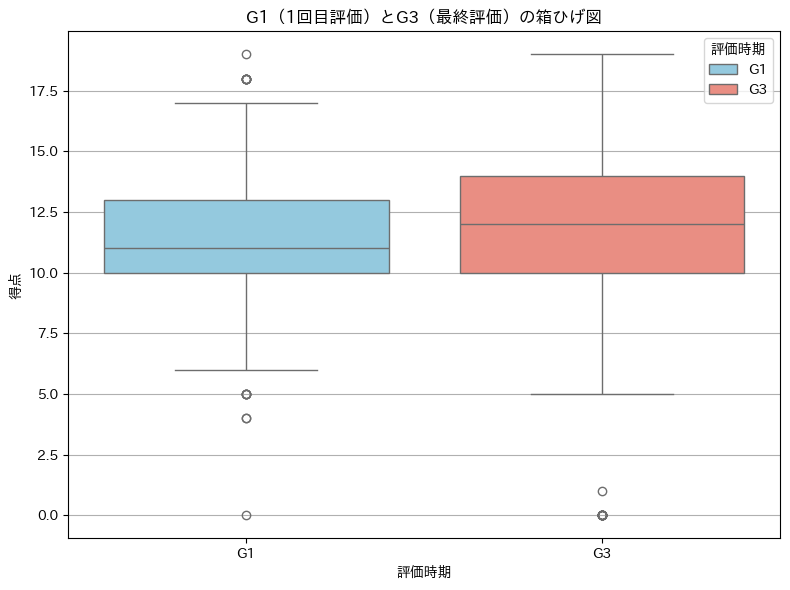
    中央値はG3のほうが大きい、全体的にG3のほうが点数高めの印象

ステップ2：正規性の確認

  • Shapiro-Wilk検定　　　 → 手法の説明はこちら
    • W値：0.811　p値：7.11e-27
    • 設定有意水準：0.05
    • 帰無仮説：棄却
    • 解釈：正規分布に従うとみなせない

    n>100では検定が厳しくなってしまうため、Anderson-Darling検定も併用

  • Anderson-Darling検定　→ 手法の説明はこちら
    • AD検定統計量：27.071
    • 設定有意水準：0.05　臨界値：0.782
    • 帰無仮説：棄却できない
    • 解釈：正規分布に従うとみなせる（厳密には「従わないといえない」）
  • Q-Qプロット

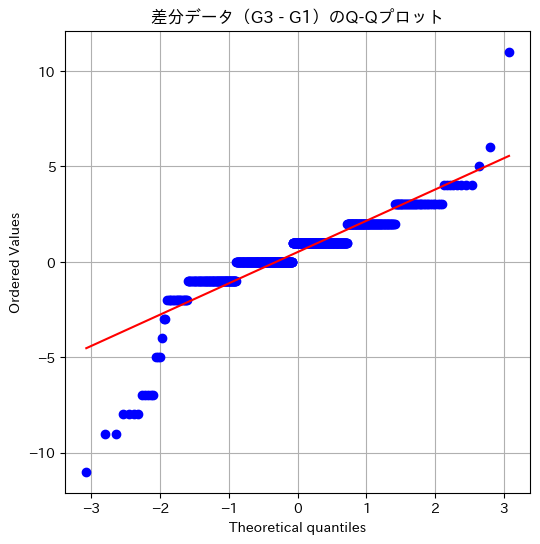
    中央付近（0付近）は点が赤線にほぼ沿っている → 中央の分布は正規分布と近い形
    両端が理想線(赤線)から大きく逸れている → 外れ値がやや多い可能性がある

  • ヒストグラム

    横軸が約0.8付近を中心にほぼ左右対称のベル型になっている → 中央付近(-5~5)は正規分布と近い形
    両端(-10,10付近)に外れ値が散見される → 正規分布とのずれがあるかもしれない

ステップ3：対応のある2群の差検定 実施

正規性検定の際に「Shapiro-Wilk検定：正規分布に従うとみなせない」「Anderson-Darling検定：正規分布に従うとみなせる」となったため、対応のあるt検定とWilcoxonの符号付順位検定の両方で評価

  • 対応のあるt検定　　　 → 手法の説明はこちら

    • t値：-7.093　p値：3.45e-12
    • 設定有意水準：0.05(両側検定)
    • 帰無仮説：棄却
    • 解釈：G1とG3で有意な差がある

  • Wilcoxonの符号付順位検定 → 手法の説明はこちら

    • W値：25595.500　p値：5.58e-24
    • 設定有意水準：0.05(両側検定)
    • 帰無仮説：棄却
    • 解釈：G1とG3で有意な差がある

示唆と次のアクション

  • 分析結果：G1とG3で統計的に有意な差がみられた
  • 今回の示唆：学期中の学習活動や指導によって、生徒の成績に何らかの変化が生じたと考える
  • Next分析案：
    • 差の方向（点数が上がったか下がったか）をさらに確認
    • 学生の属性深堀
    • 効果量の測定
  • ビジネスアクション案
    • 成績が上がった/下がった学習活動や指導を特定し、成功/失敗パターンとして横展開
    • 成績が上がった/下がった学生属性・行動を分析し、個別最適化学習や人材育成戦略へ応用

補足リンク・参考情報

Discussion