【リ・スキリング講座の分析シリーズ④】 専門実践教育訓練の効果検証チャレンジ
本分析シリーズでは、厚生労働省の「教育訓練給付金」制度の対象講座に関するスクレイピングデータを用いて、主にコストやベネフィットについてさまざまな角度から分析、可視化を行ってきました。
第1弾はこちら。
第2弾はこちら。
第3弾はこちら。
これまでの分析では、給付金のカテゴリーやサブカテゴリーごとの通学利用や通学期間、就業者向けの効果や非就業者向けの効果を可視化するために技術的分析を行い、基礎統計量の表や箱ひげ図を算出してきました。
今回は記述的分析からステップアップし、因果推論手法を用いてリ・スキリングの効果を検証することにチャレンジしてみようと思います。
あくまでも「チャレンジ」ということで、綺麗な分析とはならないですが、分析結果よりもむしろ、今回のデータセットを使ってどんな因果推論が実施できると考えたか、あるいは効果検証の限界について詳細に述べようと思います。
因果推論、その根本問題と自然実験
統計的因果推論では多くの場合、ある処置が起こったときの母集団における平均的な効果をサンプルから推定することを目指します。例えば、あるリ・スキリング講座を受講することが次期の賃金に与える影響を推定したい場合、個人iがそのリ・スキリング講座を受講したときの次期の賃金を
で算出できます。
しかし現実世界では、
これに対処するためのシンプルな方策は、処置をランダムに割り当てる、いわゆるRCT(無作為化比較実験) a.k.a. A/Bテストです。(詳細は省略します。)
処置をランダムに割り当てることで、処置群のYの平均値と統制群のYの平均値路の差が平均処置効果の推定量となり、これが不偏性、一致性を持つことが知られています。
準自然実験としてのRDD
処置をランダムに割り当てるというシンプルな操作と集計のしやすさから、A/Bテストはもはや枯れた技術といえるくらい浸透しているのではないかと思います。
一方で、今回のリ・スキリングのスクレイピングデータのような観察データでは、RCTに当てはまる分析ケースを見いだすことはほとんど困難です。
これは、興味のある処置がランダムに割り当てられているケースが稀であるからです。
例えば特定のユーザーに向けた施策の効果を推定したいとき、普通は効果がありそうなユーザーに絞ってメールやプッシュ通知を配信すると思います。この時点でランダムではないですよね。やはりA/Bテストの実行のためには、施策の実行時点で事後の効果検証を見越して施策の設計を行っている必要があると思います。
ただ、ランダムな割り当てがなされていないケースにおける観察データからも、特定のシチュエーションを見いだして因果推論を行うことができる場合もあります。その推定方法の一つが、RDD(regression discontinuity design、回帰非連続デザイン)です。この手法では、連続変数におけるある閾値の近辺においてはランダムに処置が決定されるという状況にあるという仮定の下、その閾値の左右の極限の差を処置群における平均処置効果(ATT, average treatment effect on the treated)として推定するものです。詳しくは川口、澤田(2024)の第6章を参照いただければと思います。
問題設定と着目する制度設計
今回は、「一般教育訓練受講と比較して、専門実践教育訓練給付金制度が、就業者のキャリアアップ、または非就業者のキャリアアップに与える効果」を推定することを目指します。
教育訓練給付金制度は、以下のように3種類の補助金が存在し、それぞれ給付率や最大給付額が異なります。
-
専門実践教育訓練給付金:受講費用の50%(年間上限40万円)
- 資格取得等をし、かつ訓練修了後1年以内に雇用保険の被保険者として雇用された場合に受講費用の20%(年間上限16万円)が追加支給される
- さらに訓練修了後の賃金が受講開始前より5%以上上昇した場合に受講費用の10%(年間上限8万円)が追加支給される
-
特定一般教育訓練給付金:受講費用の40%(上限20万円)
- さらに資格取得等をし、かつ訓練修了後1年以内に雇用保険の被保険者として雇用された場合に受講費用の10%(上限5万円)が追加支給される
- 一般教育訓練給付金:受講費用の20%(上限10万円)
このうち、業務独占資格又は名称独占資格に係るいわゆる養成施設の課程に該当する講座は、上記の3種類の補助金カテゴリーのすべてに該当する可能性があります。これらの講座はきゅう師や栄養士、歯科衛生士など特定の国家資格の取得を目的とする養成施設で提供される講座です。
なお、以下では議論の簡略化のために、特定一般教育訓練給付金に関する議論、説明を省略します。
これらの講座について、補助金カテゴリーを決定するのはおおまかに以下のような基準となっています。
(参照元:専門実践教育訓練給付金、特定一般教育訓練給付金、一般教育訓練給付金)
-
専門実践教育訓練給付金:
- 期間:原則1年以上3年以下
- 入講者の受験率 80% 以上
- 合格率が全国平均以上
- 就職・在職率80%以上
-
一般教育訓練給付金:
- 3年以内
- 修了者の受験率 50% 以上
上記の基準をみると、業務独占資格又は名称独占資格に係るいわゆる養成施設の課程に該当する講座が専門実践教育訓練に該当するか、あるいは一般教育訓練に該当するかを決めるのは、⓵入講者の資格等受験率 、⓶合格率 および ⓷就職・在職率 となっています。
今回のデータでは合格率と就職・在職率が計算できないため、簡略化のため入構者の受験率のみにフォーカスし、この連続変数の閾値によって給付金が分かつという状況を準自然実験とみなすことはできないかを検討してみたいと思います。川口、澤田(2024)第6章、P149の「近傍無作為化」の条件によると、今回RDDが成立するためには、
1.処置下、統計下のキャリアアップ効果の平均値が等しい
2.ぎりぎり処置を受けた人とぎりぎり処置を受けなかった人の観測頻度が等しい
3.事前の共変量の分布が等しい
これらの条件が満たされている必要があると考えられます。
これらを確かめながら、RDDでの分析が成立するか確認したいと思います。
推定チャレンジとその限界
結論から申し上げると、このチャレンジは失敗に終わりました。
その原因を、いくつか列挙したいと思います。
1. 入講者の受験率がRDDの基準となる連続変数として機能していない
今回の分析において専門実践教育訓練給付金の受講対象と一般教育訓練給付金の受講対象とを分かつとしている 入講者の受験率80% を境に、その近傍における観測数を可視化したいと思います。
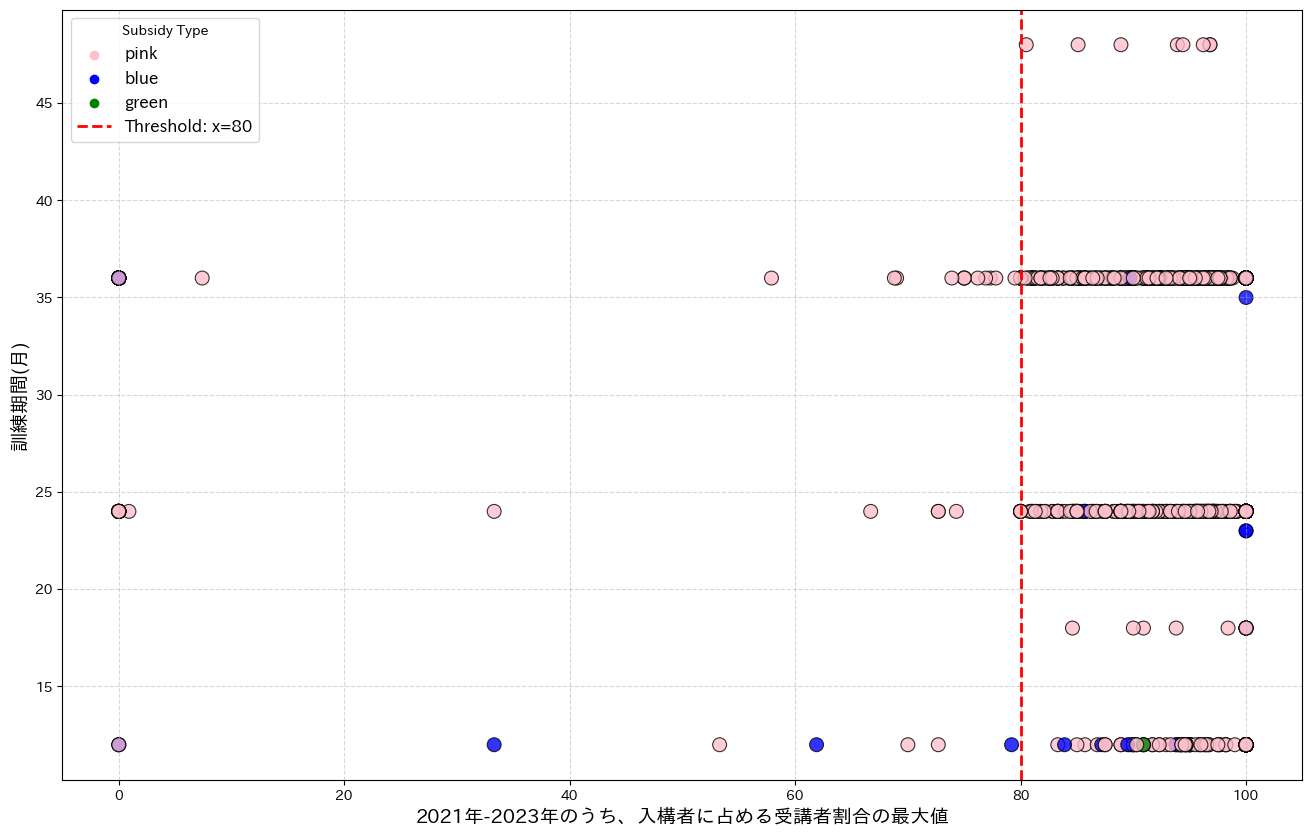
図1:業務独占資格又は名称独占資格に係るいわゆる養成施設の課程に該当する講座の、入構者の受験率と訓練機関との関係を表す散布図
上記の図において、pinkは専門実践教育訓練の、blueは一般教育訓練の、業務独占資格又は名称独占資格に係るいわゆる養成施設の課程に該当する講座の入構者の受験率と訓練機関との関係を表す散布図となっています。なお、異常値を除くために受験率が100%を超えて記載されている講座を除外しています。
確かに専門実践教育訓練のほとんどは閾値と見られる「受験率 >= 80%」を満たしていますが、それを満たしていない講座も少なくありません。また、受験率がとても小さい講座も見られます。
さらに、一般教育訓練にもこうした非遵守者がいることが分かります。
こうした非遵守者の存在それ自体が推定に大きな問題を与えるということではありません。非遵守者に一定ロバストなfuzzy RDDを用いると、閾値以上であることを示すダミー変数を操作変数と置くことで推定を目指すことが検討できます。
そのため、RDDの実行を行えない理由としてはこの点はマイナーなものです。より深刻なのは、以下の2,3の理由です。
2. サンプルサイズが小さい
RDDの仮定として「2.ぎりぎり処置を受けた人とぎりぎり処置を受けなかった人の観測頻度が等しい」が満たされているかどうかも図1から確認できます。
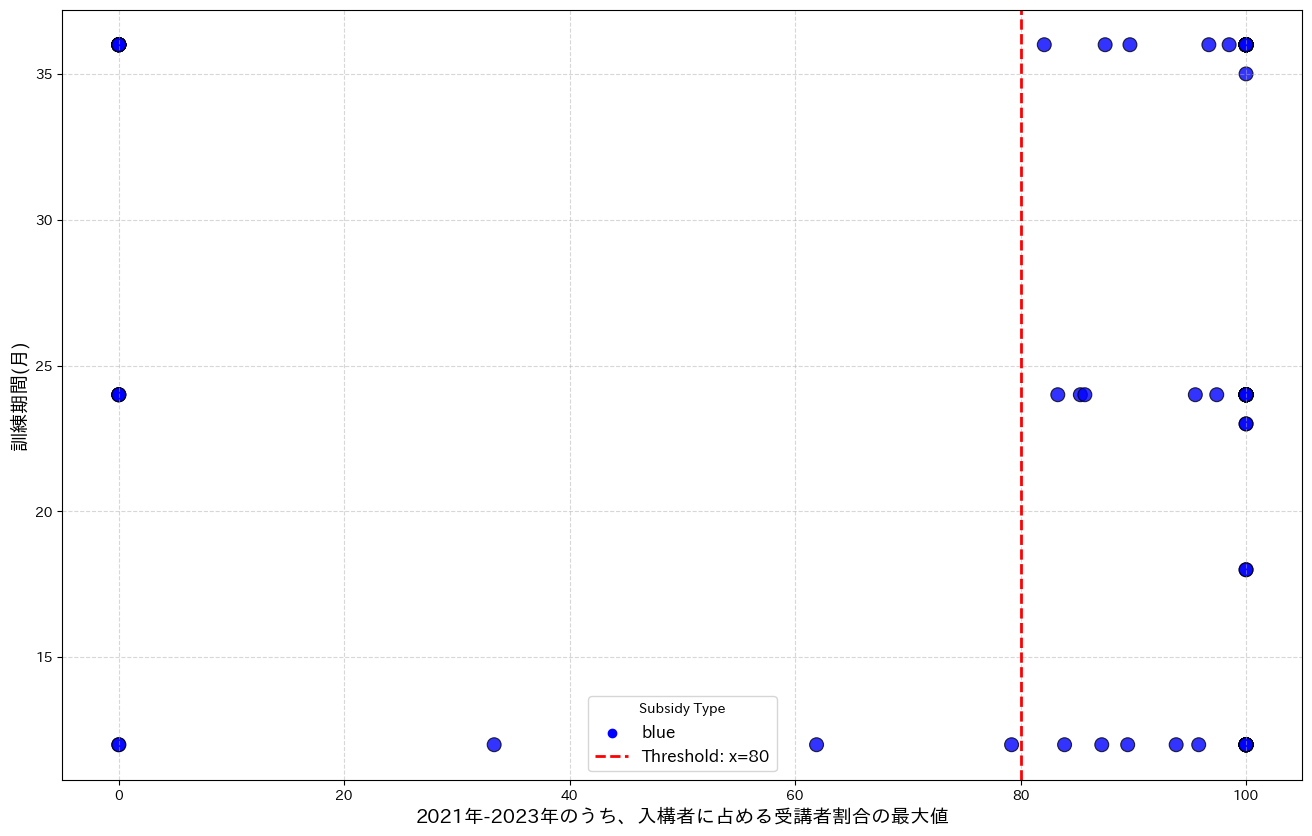
図2:業務独占資格又は名称独占資格に係るいわゆる養成施設の課程に該当する一般教育訓練講座の、入構者の受験率と訓練機関との関係を表す散布図
さらに、この図を見ると、圧倒的に一般教育訓練の講座数が少なく(122件)、閾値近傍ではさらに小さいことが分かります。この図から「2.ぎりぎり処置を受けた人とぎりぎり処置を受けなかった人の観測頻度が等しい」は満たされていると言い難く、これを推定に用いると分散が大きい推定量が算出できることが容易に想像されます。
3. 制度が複雑
これまでは⓵入講者の資格等受験率のみを各講座の給付金カテゴリーの決定基準であると簡略化してきましたが、1を見ると、やはり⓶合格率 および ⓷就職・在職率も含めて、複雑な要因によって補助金カテゴリーが決まっているようであることが推測できます。特に図2を見ると、一般教育訓練給付金の対象であるのに受験率が80%を超えているような講座も多いことが分かります。1の結果も含めて、やはり⓵入講者の資格等受験率のみを専門実践教育訓練と一般教育訓練とをわかつ条件として簡略化して用いることは不適切だった可能性が高いです。正確な推定には、各講座の合格率および就職•在職率のデータを得た上で、それらの基準が専門実践教育訓練給付金の受給基準を満たしているか否かを示すダミー変数を作成し、操作変数法で推定を目指すのが良いのではないかと思います。
また、今回のデータはあくまでも教育訓練給付金の対象講座に限られているため、セレクションバイアスが発生している可能性を否定できません。世の中のリスキリング講座がまとまって閲覧できる、代表性の高いサイトの登場を願ってやみません。
おわりに
今回は教育訓練給付金の各講座の情報が含まれるスクレイピングデータから、専門実践教育訓練の効果を推定できないか検討してみました。一見準自然実験が適用なケースでも、実際にデータを見てみると推定にハードルがあることが分かるケースも少なくないと思います。観察データから準自然実験をきれいに見いだすのは簡単ではなく、推定に必要や仮定や条件を丁寧に確認する姿勢が求められると思います。特に今回のケースでは、前述の3つの条件のうち、特に「ぎりぎり処置を受けた人とぎりぎり処置を受けなかった人の観測頻度が等しい」という条件が満たされていないと判断しました。今回は触れませんでしたが、例えば3に関しては共変量のバランスをチェックするなど、別の角度から仮定の成立を確かめる必要があります。RDDだけでなくDIDなど他の手法に関するアンチパターンを記した記事も散見されますが、各手法がどういった状況なら使えるか、理論と先行事例をもって学習していけたらと思います。
Discussion