🐈

PyMCでベイズ統計を始める

2024/01/22に公開

PyMCによるベイズ統計の始め方

Peter D. Hoff 著, 入江薫菅澤翔之助橋本真太郎訳
標準ベイズ統計学 (A First Course in Bayesian Statistical Methods)
2022-06-01
https://www.asakura.co.jp/detail.php?book_code=12267

Osvaldo Martin 著, 金子武久訳
Pythonによるベイズ統計モデリング (Bayesian Analysis with Python)
2018-06-26
https://www.kyoritsu-pub.co.jp/book/b10003944.html

PRMLや標準ベイズ統計学を読み進めている時に感じた、初学者として戸惑った観点などを忘れないうちに書き留めておきます。
ベイズの考え方から初めて、実際にPyMCでデータを記述していきます。
学部初年次の確率統計の講義でよくやる頻度論的な仮説検定で統計恐怖症になった人でも、ベイズを使うと直感的に検定を理解できるのでベイジアンに改宗すると世界が広まります。

この記事では、まず完全初心者のための「ツールとしての式の読み方」について話してから、「標準ベイズ統計学(FCBSM)」の1~2章と「Pythonによるベイズ統計モデリング(BAwP)」の1~3章を読みながらデータ分析の初歩に必要なベイズ統計のおさらいをします。

確率統計の書籍を読む前に、入り口でつまずいた人向けの「感覚」の解説メモを置いておきます。
次の2点ふわっとした雰囲気を押さえてあげれば、PRMLなどを読み始めてもある程度耐えられると思います。

ツールとしての確率分布の読み方

右も左も分からなかった頃、中学から使っていた関数 $y = f(x)$ と、大学以降の確率分布と確率変数 $y \sim p(y)$ の表記の違いが頭に入ってこなかったせいで、式を読んでも何を言ってるのかわからないことがあった。
特に式の引数と返り値について補足すると、関数は「引数(y is equal to f of x の $x$ )を入力として、 $y$ を返す」と言えるのに対して、確率分布では「引数(y is distributed as p of y の $y$ )が分布 $p$ から得られ、 $y$ は $p$ に従う」と言えて、定数と確率変数は扱う上で少し違いというか、読み替えがいる、ということを頭に置いておくと良い気がする。
上の例を似た扱いになるよう書き換えると、以下のように書ける。

\begin{aligned} y & = f(x) \\ y & \sim p(y|x) \end{aligned}

$p(y|x)$ は p of y given x といい、文字通り「xが与えられた時のyの従う分布」つまり条件付き分布である。決定的に $x$ から $y$ が定まる関数と似たことを分布でやろうとすると、「 $x$ が与えられた時の $y$ の従う分布から $y$ をサンプルする」という条件付き分布を考えることになる。条件付きというと難しそうだが、扱う上ではただ引数を持った関数的な分布だと思っていいと思う。

よく見る形としては、正規分布 $x \sim \mathcal{N}(x|μ,σ^2)$ がある。これは(ベイズ的には)平均と分散を表す確率変数 $μ,σ$ で条件付けした正規分布から $x$ が得られることを表している。

あながちこの話はいい加減ではなく、ベイズ的な回帰を考える時、予測分布は $y = p(y|x)$ の形で出てきて、この分布の持つパラメータを $y = f(x) + ε$ に対してfitする、というのは実際によくある話である。

頻度論とベイズでの母数の考え方

母数 $θ$ のことを集団のサイズやサンプルサイズの意味で使う人が多くなってる気がするが、これは誤りである。
本来は母集団の持つ統計量、つまり(頻度論的には)観測したデータを生成しているはずの真の分布の持つパラメータのこと。

頻度論的な統計とベイズ統計との根本的な考え方の違いは次のところが大きい。

頻度論: データは確率変数で、その背後にある真の分布(仮説)からサンプルされて現れたものと考える
ベイズ統計: 得られている定まったデータに対して、最も合う分布(信念)を確率変数として考える

言い換えると、頻度論は「母数は不変で、データは確率的に変わりうる」という考えで、ベイズ統計は「観測したデータは不変で、母数はデータに条件付けられた確率変数として存在する」という考えといえる。

どちらが誤っているという訳では無いが、正直なところ頻度論の統計は初心者が雑に扱うのは難しすぎる気がする... 仮説検定などは特にロジックが錯綜していて、国語力がないと「自分の足を撃つ」手法がベイズのそれより多いと思う。あと単純によくわからない。

# この記事で使うライブラリ
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns

import pymc as pm
import arviz as az
import xarray as xr
az.style.use("arviz-darkgrid")

信念と単純な例題

ここではベイズ推論に関する初歩的な解説と、PyMCで実装した簡単な例を見ることで、ベイズ統計がどんなふうに動くのか確認してみる。

確率は信念(belief)を数値的に表現するいい方法になる。
A,B,C が重複可能な事象、たとえば「おばばが小豆入りの餅を焼く」「室温が20度以上である」「正月である」という事象に対し、信念関数 $b$ は「引数に持つ事象が起こると考えられる(信じられる)度合い」を返し、その値が大きいほど確信度が高くなる。

$b(A) > b(B)$ : Aが真であることとBが真であることではAの方が確信度が高い。
$b(A|C) > b(B|C)$ : もしCが真であるとわかっていた場合に、Aが真であることとBが真であることではAの方が確信度が高い。
$b(A|B) > b(A|C)$ : Bが真である場合とCが真である場合では、Bが真である場合のほうがAの確信度が高い。

この信念を表すためには以下の公理を満たしてほしいという要求がある。

信念の公理

$b(\texttt{not} C | C) ≤ b(A|C) ≤ b(C|C)$ : 条件付き信念は、完全な不審 $b(\texttt{not} C | C)$ と完全な信頼 $b(C|C)$ に割り当てる値で上下から抑えられる。
$b(A \texttt{or} B | C) ≥ \max(b(A|C) , b(B|C))$ : 2つの事象への信念は、事象どちらかの信念の値の大きい方になる。つまりどちらかの事象に対して「他の可能性」を追加しても減少することはないということ。
$b(A \texttt{and} B | C)$ は $b(B|C)$ と $(A | B \texttt{and} C)$ から計算可能: Cが真の時AとBが真であるか判断するために次の計算が必要になる。
1. Cが真の時のBを判断する。
2. Bが真ならば、BとCが真の時のAを判断する。

確率の公理

$0 = p(\texttt{not} C | C) ≤ p(A|C) ≤ p(C|C) = 1$
$A \cap B = ∅ \implies p(A \cup B|C) = p(A|C) + p(B|C)$
$p(A \cap B | C) = p(B|C) p(A|B \cap C)$

上を見ればなんとなくそんな感じがすると思うが、確率の公理は信念の公理を満たしていて、ベイズ推論では信念を確率として表現する妥当性がわかると思う。

ベイズ推論

ベイズ推論(Bayesian inference)は集団の特性を表現するパラメータ $θ \in \mathcal{Θ}$ と、集団の部分数合がデータ $y \in \mathcal{Y}$ として値を得られる時、 $y$ から得られる情報は集団の特性に関して不確実性(uncertainty)を減らしてくれる。この不確実性の変化を測ることがベイズ推論の目的である。

BAwPの言い方を借りれば、 $p(y=\texttt{y}) = \frac{1}{2}$ と $p(y=\texttt{y}) = \frac{4}{8}$ ではどちらも $\texttt{y}$ が起こる確率は1/2だが、後者の方がデータ多くのデータが1/2になるという情報を形成しているので、不確実性が低くなっているといえる。

以下では、標本や信念に関して考えて、ベイズの学習の過程を見ていく。

$\mathcal{Y}$ : 標本空間。全てのデータが所属していて、実際に得られるデータ $\{ y_n \}$ はこの空間から得られる。
$\mathcal{Θ}$ : パラメータ空間。あり得る全てのパラメータの値がここに含まれていて、この中から母集団の真の特性を表すパラメータ、つまり母数を見つけたい。

$y, θ$ に関する信念を、同時に $\mathcal{Y}, \mathcal{Θ}$ 上の確率分布として表現することで、パラメータを見つける。

$p(θ)$ : 事前分布(prior distribution)。各 $θ \in \mathcal{Θ}$ が母集団の真の特性をどれだけ表しているかに対する私達の信念。
$p(y|θ)$ : 尤度(likelihood)あるいは標本モデル。もし $θ$ が真の特性を表すパラメータであれば、データ $y$ が結果得られるだろう、という信念の強さ。つまり $θ$ のデータへのfit具合。fitしていれば大きくなる。

データを観測して $y$ が得られた後、尤度のデータfitが計算できるので、ベイズの定理から事前分布を更新し新たな信念を得られる。

$p(θ|y)$ : 事後分布(posterior distribution)。データ $y$ を観測した後に $θ$ がどれだけ正しいと信じられるか。

上の話は次の式で表せる。分母の周辺尤度(エビデンス)は規格化定数なのでツールを使う上ではあんまり気にしなくて良い。
ちなみに尤度原理という考えがあり、「データは全て尤度に入っている必要がある」というもので、今回の例でも式を辿ればデータ $y$ は尤度にしか入っていない変形ができることがわかる。これを満たさない分析はよくないらしい。

p(θ|y) = \frac{p(y|θ) p(θ)}{\int_Θ p(y|θ) p(θ) dθ}

複雑な統計の問題に頻度論的な推論方法は、往々にして自明でない。しかしベイズルールでは同じような感じで推論を構成できて、性能比較に頻度論的な方法を併用することもできる。便利で上手くいく。

稀な事象の発生確率を推定する

FCBSM 1.2.1 で例示されている問題をPyMCで実装して、実際に見てみる。

ある町の感染症の有病率について、20人の町民に対して調査を行った。
関心があるのは町内の感染者の割合 $θ$ であり、町民のうち感染者数が $y \in \{ 0, 1, \dots 20 \}$ で表せるとする。

\begin{aligned} Θ & = [0, 1] \\ \mathcal{Y} & = \{0,1,2, \dots ,20\} \end{aligned}

まず、尤度と事前分布を決める。
尤度に関して、全体 $N$ 人のなかで感染率 $p$ の疾病に罹患した感染者の総数 $y$ を表せる分布は、2項分布(binomial distribution)だ。

\begin{aligned} y & \sim \text{Bin}(y|N=20, p=θ) \\ \text{Bin}(x|N,p) & = _N \text{C}_x p^x (1-p)^{N-x} \end{aligned}

そして、 $θ$ が取る範囲は0から1の間で、どうやら事前情報によると有病率は0.10近辺らしいという情報を私達は持っているとする。
ここで、尤度として2項分布を定めたことで、事前分布としてβ分布(beta distriburion)を定めると便利になる。というのも、尤度である2項分布とβ分布の積は、β分布に戻ってくれて、その分布は $\text{Beta}(θ|α+y, β+N-y)$ になることがわかっている。こういうものを共役事前分布 といい、扱いやすいのでよく使われる。
β分布に従うθは期待値 $\mathbb{E}[\frac{α}{α+β}]$ になり、今回 $\text{Beta}(θ|α=2, β=20)$ を選べば期待値は0.09で、事前情報通り0.10近辺になっている。

\begin{aligned} θ & \sim \text{Beta}(θ|α=2, β=20) \\ \text{Beta}(x|α,β) & = \frac{Γ(α+β)}{Γ(α)Γ(β)} x^{α-1}(1-x)^{β-1} \end{aligned}

# まずモデリングに使った分布を可視化してみる

fig, axes = plt.subplots(1, 2, figsize=(10,5))

N = 20

# fig Bin(x|n,p)
p_list = [0.1, 0.2, 0.3, 0.5, 0.8]
x = np.arange(N)
for p in p_list:
    y = stats.binom(n=N, p=p).pmf(x)
    axes[0].plot(x, y, "-o", label=f"p = {p}")
axes[0].legend()
axes[0].set_xticks([0,5,10,15,20], [0,5,10,15,20])

# fig Beta(x|a,b)
a_list = [0.2, 1, 2, 2, 1]
b_list = [0.5, 1, 1, 3, 3]
x = np.linspace(0, 1, 20)
for a, b in zip(a_list, b_list):
    y = stats.beta(a=a, b=b).pdf(x)
    axes[1].plot(x, y, label=f"a = {a}, b = {b}")
axes[1].legend()

以上のモデリングが終われば、後はデータを入手してベイズ推論を計算するだけで、この町の有病率に対する信念がどれだけ合っていたか、データを見た後どのような信念に変わったかを確認することができる。今回は町内に感染者がいなかった( $y=0$ )の場合を見る。

PyMCではpm.Model内に分布を登録してサンプリングによる近似で周辺尤度などをいい感じに計算して事後分布を出してくれる。
事前分布とobservedでデータを観測する分布(つまり尤度)を与えて、最後にpm.sampleで「推論ボタン」を押せば勝手に計算してくれる。(といいつつ今回のモデルは手計算で事後分布が求まるのであまり有効ではない)

# 観測データ
N = 20
y = np.zeros(N).sum()  # 感染者数
alpha = 2
beta = 20

# PyMCによる計算
with pm.Model() as model:
    theta = pm.Beta("theta", alpha=alpha, beta=beta)
    y_pred = pm.Binomial("y_pred", n=N, p=theta, observed=y)
    trace = pm.sample(2000, chains=4, cores=1)
trace = trace.sel(draw=slice(200, None))  # burn-in

az.plot_trace(trace)  # 事後分布の可視化
az.plot_autocorr(trace, combined=False)  # サンプリング時の自己相関
az.summary(trace)  # 計算結果の要約

#       mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
# theta	0.048	0.033	0.002	0.108	0.001	0.0	2254.0	2296.0	1.0

計算結果はtraceに格納されていて、pm.sampleで渡したサンプリング回数drawsと試行回数chainsの分だけデータが入っている。いくつか図を表示したが、これらは計算結果を確認するのに役立つ。

az.plot_trace: サンプリング結果のKDEと、サンプリング過程で得られた素のサンプル値。サンプル値は変に規則性がない方が良い。
az.plot_autocorr: サンプリング過程の各値の自己相関。自己相関が高いのは良くない。
az.summary: 計算結果の要約を出してくれる。r_hatはGelman-Rubinテストの値で、1.1未満ならいい感じに計算が収束している。

PyMCではデータの受け渡しにxarrayという名前付きのNumPy配列を扱う。
今回のtraceの出力は主に「Data variables」、「Coordinates(chain, draw)」の軸(次元)があり、InferenceData.posterior["parameter"]のようにアクセスできる。

> trace

Inference data with groups:
	> posterior
	> sample_stats
	> observed_data


> trace.posterior

<xarray.Dataset>
Dimensions:  (chain: 4, draw: 1800)
Coordinates:
  * chain    (chain) int64 0 1 2 3
  * draw     (draw) int64 200 201 202 203 204 205 ... 1995 1996 1997 1998 1999
Data variables:
    theta    (chain, draw) float64 0.03886 0.0366 0.04764 ... 0.04298 0.0689
Attributes:
    created_at:                 2024-01-21T08:16:52.272755
    arviz_version:              0.13.0
    inference_library:          pymc
    inference_library_version:  5.9.0
    sampling_time:              1.9531362056732178
    tuning_steps:               1000


> trace.posterior["theta"]

<xarray.DataArray 'theta' (chain: 4, draw: 1800)>
array([[0.03886133, 0.03659619, 0.04764218, ..., 0.03289611, 0.01826896,
        ...
        0.00704132, 0.00761786, 0.01328384, ..., 0.06280299, 0.0429803]])
Coordinates:
  * chain    (chain) int64 0 1 2 3
  * draw     (draw) int64 200 201 202 203 204 205 ... 1995 1996 1997 1998 1999

Burn-in: 可視化ライブラリArvizのtutorialのように、traceの最初の方のサンプル結果を消すことがよくある。これはplot_autocorrの図をみれば分かる通り、最初の方は自己相関が高いのでうまい結果ではないからである。今回の例では最初の200サンプルを削っているので、上のdrawが200から始まっているのがわかる。
ちなみに、InferenceData.sel(draw=slice(100, 200))のようにすれば、drawの軸を100以前と200以降を捨てることを意味する。

結果をもう少しよく見てみる。

最高密度区間(Highest Density Interval; HDI): よく使われるのは95%HDIや98%HDI。その区間にパラメータが存在する確率。ベイズの信用区間(credible interval)を意味する。

実質同値域(region of partical equivalence; ROPE): 予め定めておく仮説区間。ROPEとHDIの重複ぐあいで「仮説が妥当か、そうでないか」を論じることができる。

今回の問題では、他の町での有病率は0.10で、データを取った町でも大体0.08から0.12くらいの間になるだろうと考えられた。以下の右の図は事前分布(水色)とサンプリングで計算した事後分布(青)、その事後分布をβ分布で引き直した補助線(赤)を示していて、ROPEは[0.09, 0.11]の区間を示しており、オレンジ色の直線が0.10のラインである。

fig, axes = plt.subplots(1, 2, figsize=(15,5))

# chainごとの最高密度区間を表示
az.plot_forest(trace, var_names=["theta"], ax=axes[0])

# 事前分布(cyan)と事後分布(blue)、HDI、ROPEを表示
az.plot_posterior(trace, var_names=["theta"], rope=[0.09, 0.11], ref_val=0.10, ax=axes[1])
t = np.linspace(0, 0.26, 50)
axes[1].plot(t, stats.beta(a=alpha, b=beta).pdf(t), color="c")
axes[1].plot(t, stats.beta(a=2, b=40).pdf(t), color="r", alpha=0.8)

θの事後分布をみればわかる通り、事前分布よりも小さな有病率を信じるようになったことがわかる。定めたROPEはHDIを含んで入るものの少しだけはみ出しており、有病率の仮説の正誤は保留となっている。

最後に事後分布と事前分布からデータをサンプルしたらどうなるか見てみる。

spost = pm.sample_posterior_predictive(trace, model=model)
az.plot_ppc(spost, num_pp_samples=50, kind="scatter")

感度分析

事後分布を使った計算により、事前知識が事後分布にどのように影響を与えるか見ることもできる。
先程の議論で出てきた事後分布の閉形式 $\text{Beta}(θ|α+y, β+N-y)$ の期待値を考えると次のようになる。

\begin{aligned} \mathbb{E}[θ_{\text{posterior}}|y] & = \frac{α+y}{α+β+N} \\ & = \frac{N}{α+β+N} \frac{y}{N} + \frac{α+β}{α+β+N} \frac{α}{α+β} \\ & = \frac{N}{w+N} \bar{y} + \frac{w}{w+N} \mathbb{E}[θ_{\text{prior}}] \end{aligned}

つまり、β分布の事後分布の平均は、データで決まる項と事前分布で決まる項に分解できて、 $w = α+β$ は事前知識への自信を表している。予め、事前の予想パラメータ $θ_{\text{prior}}$ と自信の程度 $w$ を提示してくれれば、それらを使って $θ_{\text{posterior}}$ へ対する事前の信念を、 $α = wθ_{\text{prior}}$ と $β = w(1-θ_{\text{prior}})$ のβ分布で近似できるということである。

この式による計算を意思決定へ活かす事もできる。
例えば保険機関が市民にワクチン接種を推奨する広告を打つか打たないか判断しようと思った時、現在の感染率が0.10より大きいと強く確信しているならば広告を打てばいい。自信がない( $w$ が小さい)または予想感染率 $θ_{\text{prior}}$ が低い場合、データを見た後90%くらいの確度で感染率 $θ_{\text{posterior}} < 0.10$ となり、まあ広告は打つほどでもないかなぁとなる。さらにもともと感染率を低く見積もっていた人であれば、データを見た後はもっと高い確度で感染率 $θ_{\text{posterior}} < 0.10$ を信じることになる。

頻度論的な方法との比較

母集団比率 $θ$ の推定量として標本平均 $\bar{y} = \frac{y}{N}$ を使うと、今回は町内の感染者が0人だったので推定値も0になる。頻度論の不確実性の評価としてWald区間 があり、 $θ$ の95% 信頼区間(confidence interval)を計算できる。

\text{confidence interval} = \bar{y} ± \sqrt{\frac{\bar{y}(1-\bar{y})}{n}}

信頼区間はcorrect asymptotic frequentist covrage、つまり $n$ が十分大きくなれば95%の確率で $θ$ を含むような $y$ をとるようになる。しかし今町内のデータでは信頼区間も0の一点になってしまい、正確な表現ができなくなってしまう。

また、調整Wald区間というものがよく使われるようになっていて、その式はベイズ的な味方をすれば事前分布 $\text{Beta}(2,2)$ を事前分布とした時の $θ$ の事後分布になっている。

\begin{aligned} \text{confidence interval} & = \hat{θ} ± \sqrt{\frac{\hat{θ}(1-\hat{θ})}{n}} \\ \hat{θ} & = \frac{n}{4+n} \bar{y} + \frac{4}{4+n} \frac{1}{2} \end{aligned}

以上のように、ただ標本平均を取るだけではサンプル数が少ない時、母集団平均 $θ$ の推定量というよりだだの標本データの要約量でしかないが、「最善の予想」 $θ_{\text{prior}}$ と予想の確度 $w$ を使って調整した推定量を考えれば、予想の効果を使って推定量を安定させることができる。

階層モデルによるベイズ推論

前の章では頻度論的な不確実性の表現よりもベイズ推論が自然に不確実性を表現できていて、信念などの扱いで事前知識と結果の意思決定に影響を与えることができることを見てきた。
次は、前章の問題を便利に解決できる階層モデルについて見てから、複数のグループに跨るデータの分析を行う。

階層モデル

事前分布についてのパラメータを更に事前分布で束縛することで、パラメータが多いモデルもロバストな推論ができるようにする。というのも、パラメータは少ない方が解釈性や汎化性能がいい(バイアスとバリアンスの問題)が、多いほうが複雑な事象をモデリングできるので、どっちも捨てがたいという課題があり、階層モデルではこのパラメータ数からくる複雑さも最適化できるという嬉しさがある。

具体的にいうと、まずデータ $y$ とパラメータ $\bold{θ}$ を使った尤度 $p(y|θ)$ を考える時、さらに $θ$ に関する事前知識を $p(θ|θ_{\text{hyp}})$ とその事前分布 $p(θ_{\text{hyp}})$ でモデリングして考えるというもので、これらを使って事後分布 $p(θ|y)$ を以下のように表現する。

\begin{aligned} p(θ|y) & ∝ p(y|θ) p(θ|θ_{\text{hyp}}) \\ p(θ,θ_{\text{hyp}} | y) & ∝ p(y|θ) (θ|θ_{\text{hyp}}) p(θ_{\text{hyp}}) \end{aligned}

これにより事前分布の情報が不十分で多義的な解釈ができてしまう場合でも、多パラメータについてロバストに推論できるようになる。実際の応用では、ハイパラ $θ_{\text{hyp}}$ についての周辺分布 を最大化する $θ_{\text{hyp}}$ を点推定してそれを使う。ここで $p(θ_{\text{hyp}}) = \text{Uniform}(θ_{\text{hyp}})$ を選べば、周辺尤度 $\int p(y|θ) p(θ|θ_{\text{hyp}}) dθ$ を最大化する $θ_{\text{hyp}}$ を選ぶことと等価になる。このような点推定値を使うことは特に経験ベイズ という。

以下では、前章の町の有病率についての問題を階層ベイズで推論したPyMCのコードで、パラメータ $α, β$ の事前分布に半コーシー分布を使ったものと、普通に推定したものを比較している。

# 観測データ
N = 20
y = 8  # 感染者数 今回は 8/20人 が感染したことにする

with pm.Model() as model_nomal:
    alpha = 2
    beta = 20
    theta = pm.Beta("theta", alpha=alpha, beta=beta)
    y_pred = pm.Binomial("y_pred", n=N, p=theta, observed=y)
    trace_nomal = pm.sample(2000, chains=2, cores=1)
trace_nomal = trace_nomal.sel(draw=slice(100, None))

az.plot_trace(trace_nomal)
plt.show()
az.plot_posterior(trace_nomal, var_names=["theta"])
plt.show()

with pm.Model() as model_hierarchical:
    alpha = pm.HalfCauchy("alpha", beta=5)
    beta = pm.HalfCauchy("beta", beta=5)
    theta = pm.Beta("theta", alpha=alpha, beta=beta)
    y_pred = pm.Binomial("y_pred", n=N, p=theta, observed=y)
    trace_hierarchical = pm.sample(2000, chains=2, cores=1)
trace_hierarchical = trace_hierarchical.sel(draw=slice(100, None))

az.plot_trace(trace_hierarchical)
plt.show()
az.plot_posterior(trace_hierarchical, var_names=["theta", "alpha", "beta"])
plt.show()

今回の設定ではデータ上の有病率は0.40%で、最初に事前知識を強く与えたモデルでは $θ=0.24$ 、階層モデルを使った場合は $θ=0.41$ となり、階層モデルの方が真値に近い結果が出た。
他にも、前章と同じ設定の0人で行った場合も階層モデルの方がデータに近い推測をしてくれる、言い換えれば設定した事前分布の効果を強く受けすぎないという便利さがある。これは良いことばかりでもないが、特に予想に自信がもてない場合は、頻度論よりは不確実性をある程度説明してくれながら、データにfitした推論をしてくれる、という点で使いやすいモデルを作れると思う。

複数グループに跨るデータ分析

階層モデルの簡単な挙動について見たところで、もっと有益な性質について見ていく。

縮小(shrinkage): 各グループのデータがハイパー事前分布を通じて情報を共有することで、共通の平均値に向かって動くこと。

以下のコードでは次の問題を扱うことで、階層モデルによる収縮を確認する。
問題として、ある都市の3つの川の汚染度が、やばい(1)か、やばくない(0)かを、1つの川の30箇所からサンプルすることで、河川の状況を調べたいというシチュエーションを考える。それぞれの川の合計汚染度をベルヌーイ分布(2項分布の各試行の2値版)で尤度をモデリングし、β分布による各川の汚染度を推測する。

\begin{aligned} θ_α & \sim \text{HalfCauchy}(θ_α | β=5) \\ θ_β & \sim \text{HalfCauchy}(θ_β | β=5) \\ θ & \sim \text{Beta}(θ | α=θ_α, β=θ_β) \\ y & \sim \text{Bern}(y | p=θ) \end{aligned}

以下のコードでは、3つの川の汚染サンプルから総合的な汚染度%を推定するものである。

def make_data(g_sample, n_sample):
    n = len(n_sample)
    groupe_idx = np.repeat(np.arange(n), n_sample)
    data = []
    for i in range(3):
        data.extend(np.repeat([1,0], [g_sample[i],n_sample[i]-g_sample[i]]))
    return data, groupe_idx  # データ数はn_sampleの合計、データ内容はg_sample個の汚染と(n_sample-g_sample)個の非汚染


def infer(data, groupe_idx):
    with pm.Model() as model:
        alpha = pm.HalfCauchy("alpha", beta=5)
        beta = pm.HalfCauchy("beta", beta=5)
        theta = pm.Beta("theta", alpha=alpha, beta=beta, shape=3)
        y_pred = pm.Bernoulli("y_pred", p=theta[groupe_idx], observed=data)
        trace = pm.sample(2000, chains=2, cores=1, progressbar=False)
    trace = trace.sel(draw=slice(100, None))

    az.plot_posterior(trace, var_names=["theta"])
    plt.show()
    return trace


n_sample = [30, 30, 30]  # データに含まれる、グループ毎のサンプル数
g_sample = [18, 18, 18]  # グループに含まれる、汚染がやばいサンプルの個数
n = len(n_sample)
data, groupe_idx = make_data(g_sample, n_sample)

# groupe_idx = [
    # 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 
    # 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 
    # 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
# ]
# data = [
    # 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 
    # 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 
    # 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0
# ]

infer(data, groupe_idx)  # サンプル中の汚染 [18, 18, 18] の場合

g_sample = [3, 3, 3]
data, groupe_idx = make_data(g_sample, n_sample)
infer(data, groupe_idx)  # サンプル中の汚染 [ 3,  3,  3] の場合

g_sample = [18, 3, 3]
data, groupe_idx = make_data(g_sample, n_sample)
infer(data, groupe_idx)  # サンプル中の汚染 [18,  3,  3] の場合

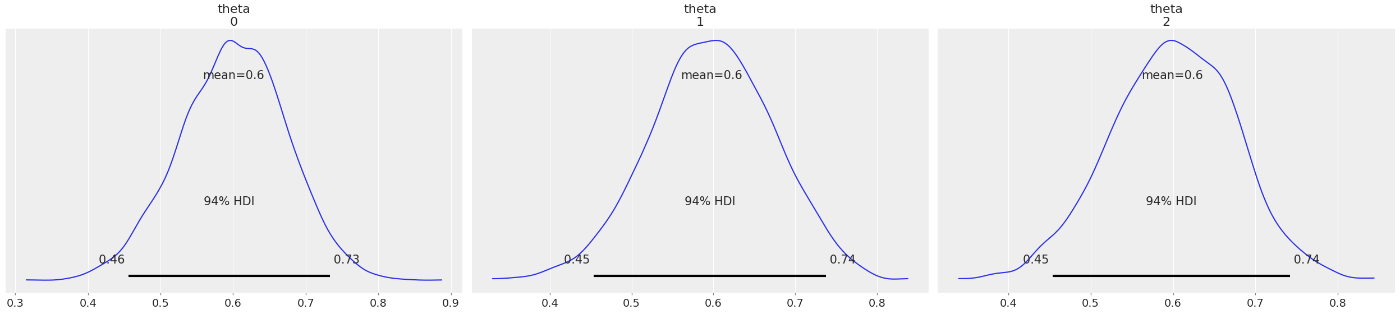
結果の通り、各川の汚染サンプルが[18, 18, 18]の場合の $θ$ 、つまり汚染度の平均は[60%, 60%, 60%]で、[3, 3, 3]の場合は[11%, 11%, 11%]だった。ここまでは普通だが、[18, 3, 3]という、一つの川で汚染が強まっている状況では、推定される $θ$ が[54%, 13%, 13%]になった。つまり、階層モデルによる収縮が起こって、グループ間の汚染状況が加味されて不確実性が考慮された平均が推測されたのである。

収縮に関する数学的な話が見当たらなかったので深煎りしないが、この性質を使うことで、データセット内のあるグループにデータがほんの少ししかないような状況が発生した時でも、そのグループにも確からしい推測ができるようになる、つまり情報が伝播してグループ単位のロバスト性が現れる、という良さをもたらしてくれるように思う。

ロバスト推論

以上の話題が理解できて使えるようになれば、もうベイズっぽい本を読み始める準備はできたと思う。内容はかなり薄まってしまっているが、FCBSMの1章とBAwPの1~3章の内容はだいたいこんな感じの話を詳しくしてくれている。
FCBSM 1章の最後では線形回帰モデルにおけるスパース回帰などを題材に予測分布について触れられている。ここではBAwP 3.2.2のロバスト推定について少し詳しく扱って、spike-and-slab回帰の話題は文字面だけ紹介しておく。

StudentT分布による推論

StudentT分布: 正規分布の裾を重くしたような形の分布で、ガウス分布よりも外れ値に引っ張られない推論ができる。例えば上の水質調査の例で言えば、1箇所だけ水質が悪くても他が全部綺麗だったら、その1箇所は無視して推測してしまおうという挙動が起こる。PRML 2.3.7に詳しく載っている。

\text{St}(x|μ,λ,ν) = \frac{Γ(\frac{ν}{2}+\frac{1}{2})}{\frac{ν}{2}} \sqrt{\frac{λ}{πν}} (1+ \frac{λ(x-μ)^2}{ν})^{-\frac{ν}{2}-\frac{1}{2}}

奇っ怪な式だが、これは正規分布とその分散の共役事前分布であるガンマ分布の階層モデルを周辺化して、あと変数をゴネゴネすると出てくる割と正統派な分布である。自由度 $ν$ が1の時コーシー分布になり、無限に飛ばすと正規分布に戻る。 $λ$ は精度(分散の逆とは限らない)を示すスケールパラメータである。
これを使って、正規分布との違いを見てみる。

nu = [100, 1, 0.1]
x = np.linspace(-10,10,200)

fig, axes = plt.subplots(1, 2, figsize=(10,5))

for n in nu:
    x_pdf = stats.t(n).pdf(x)
    axes[0].plot(x, x_pdf)

x_pdf = stats.norm(0, 1).pdf(x)  # 正規分布
axes[1].plot(x, x_pdf)
x_pdf = stats.cauchy().pdf(x)  # コーシー分布
axes[1].plot(x, x_pdf)

# データ作成
data = np.concatenate([stats.norm(0, 1).rvs(45), stats.norm(10, 1).rvs(5)])

# 推論 正規分布
with pm.Model() as model:
    mu = pm.Normal("mu", mu=0, sigma=5)
    sigma = pm.HalfNormal("sigma", sigma=5)
    y_pred = pm.Normal("y_pred", mu=mu, sigma=sigma, observed=data)
    trace = pm.sample(2000, chains=2, cores=1, progressbar=False)
az.plot_posterior(trace)
plt.show()

g_mu = trace.posterior["mu"].values.mean()  # 推論結果の分布の期待値を点で求める
g_sigma = trace.posterior["sigma"].values.mean()


# 推論 StudentT分布
with pm.Model() as model:
    mu = pm.Normal("mu", mu=0, sigma=5)
    sigma = pm.HalfNormal("sigma", sigma=5)
    nu = pm.Exponential("nu", lam=1/30) 
    y_pred = pm.StudentT("y_pred", mu=mu, sigma=sigma, nu=nu, observed=data)
    trace = pm.sample(2000, chains=2, cores=1, progressbar=False)
trace = trace.sel(draw=slice(100, None))

az.plot_posterior(trace)
plt.show()

t_mu = trace.posterior["mu"].values.mean()
t_sigma = trace.posterior["sigma"].values.mean()
t_nu = trace.posterior["nu"].values.mean()


# データにfitしているか確認
fig, axes = plt.subplots(1, 2, figsize=(10,5))

sns.kdeplot(data, ax=axes[0])
axes[0].vlines(g_mu, 0, 0.2, color="m", linestyles="dotted")
axes[0].vlines(t_mu, 0, 0.2, color="c", linestyles="dotted")

x_pdf = stats.norm(g_mu, g_sigma).pdf(x)
axes[1].plot(x, x_pdf, color="m")
axes[1].vlines(g_mu, 0, 0.3, color="m", linestyles="dotted")

x_pdf = stats.t(t_nu, t_mu, t_sigma).pdf(x)
axes[1].plot(x, x_pdf, color="c")
axes[1].vlines(t_mu, 0, 0.3, color="c", linestyles="dotted")

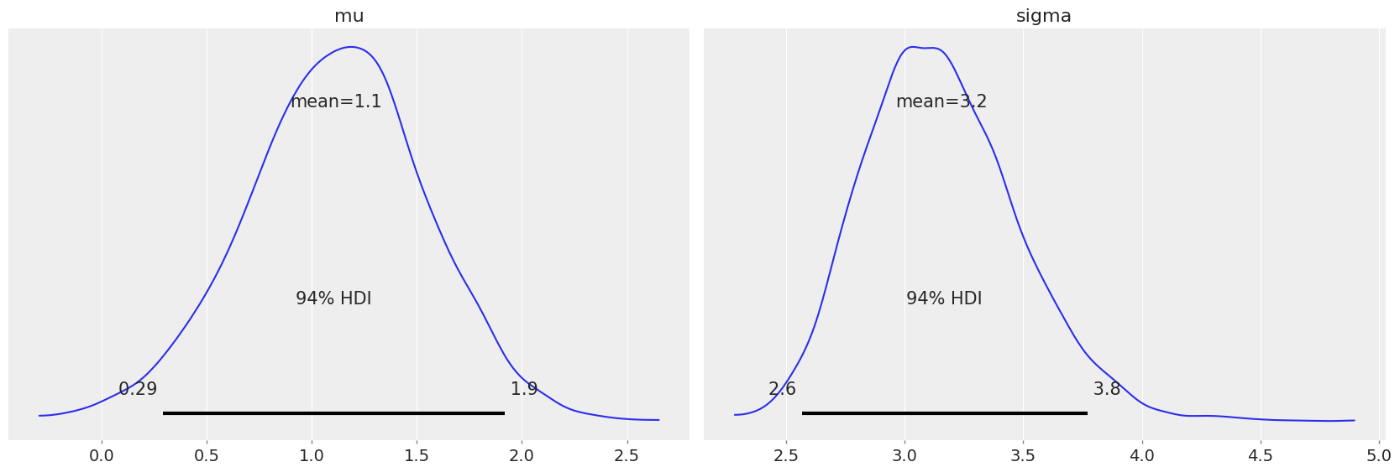
結果を見る通り、正規分布では小さなコブに引っ張られて平均 $μ$ が動いて分散も高くなっているが、StudentT分布ではちゃんと多数派のコブのみの平均に近い値を推測できている。

この記事を通して、推論で出た分布の平均を取ってグラフを書いているので、あまりベイズのご利益を受けていないことに注意。ベイズ的な方法は、「事前に持っている信念が、データを受けてどのように変化したか、その不確かさが確率分布として得られる」ことであり、高度なことをするようになって初めて嬉しさがわかってくるものだとも言える。

このロバスト性は、回帰などで言うRedgeやLassoなどに近い感覚で、正則化項の強さを事前分布に語らせることで変数選択を暗黙的に行っている(?)感じの計算から来ている。もとより、正規分布を事前分布として使った線形回帰は、式展開するとRedge回帰になっていることがわかり、Lassoなどもラプラス分布を事前分布にした方法として導ける(らしい)。モデル比較の文脈でも出てくるが、バイアス-バリアンス分解や前述の調整Wald区間など、ベイズ的観点からモデルを扱うことで正則化 に関する知識がたくさん得られる。

FCBSM 1.2.2 ではspike-and-slab事前分布 を使ったスパースな(つまり変数選択を正則化とした)線形モデルによる重回帰を例示している。(最初から飛ばしすぎな内容なので最初読む分には完全に理解する必要はないかもしれない...)

FCBSMの方は読み進めている途中だが、データサイエンティストで有名なTJOさんが書評を出していた。

宣伝

以下の記事ではPyMCによる一般化線形モデル、モデル比較、ガウス過程というようなベイズ初心者3点セットの勉強ノートを残している。線形回帰より後の記事はある程度正確だと思うので、勉強の順番の目次として活用してもらえたらうれしい。