Bayesian Analysis with PyMC 勉強ノート 4 線形モデル
Osvaldo Martin 著 金子 武久 訳
Pythonによるベイズ統計モデリング
2018-06-26
https://www.kyoritsu-pub.co.jp/book/b10003944.html
Pythonによるベイズ統計モデリング(PyMCでのデータ分析実践ガイド)を読んだので学習メモを残します。学習中のノートなので正確ではないかもしれません。また、使われているコードをPyMC3からPyMC5に書き直しました。
線形回帰モデル
次のライブラリを使用する。
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
import pandas as pd
import seaborn as sns
import pymc as pm
import arviz as az
az.style.use("arviz-darkgrid")
非ベイズの統計で用いられるロジスティック回帰や分散分析や共分散分析も、線形回帰モデルの亜種である。
- 線形回帰
- 頑健線形回帰
- 階層線形回帰
- 多項式回帰
- 線形重回帰
について扱い、線形回帰モデルと相互作用について学ぶ。
1. 線形単回帰
従属変数(dependent variable, predicted variable, outcome variable)を予測する。
従属変数は、独立変数(independent variable, predictor variable, input variable)に従属し、この各変数にどれだけ依存しているかを推測したい。
機械学習(machine leraning; ML): データの中から自動的に学習する方法の総称
上の線形回帰の式は基本的な考えでは最小二乗法などで2乗誤差最小化の最適化問題として解くことができる。これをベイジアンの考えで考えれば、「データyが平均
y \sim \text{Normal}(μ=α+βx, σ=ε) α \sim \text{Normal}(μ_α, σ_α) β \sim \text{Normal}(μ_β, σ_β) ε \sim \text{HalfCauchy}(σ_ε)
事前分布を広く取れば実質的には最小二乗法と変わらない値へ収束する。
# 直線 y = a + b*xから観測されたノイズe付きデータの作成
N = 100
a_real = 2.5
b_real = 1.5
e_real = np.random.normal(0, 0.5, N)
x = np.random.normal(0, 0.5, N)
y_real = a_real + b_real * x
y = y_real + e_real
print(x.shape, y.shape)
plt.plot(x, y_real)
plt.scatter(x, y)

# y_i = a + b*x_i + N(0,s)から観測されたデータ{x_i, y_i}から、{a, b, N(0,s)}をベイズ推定する
with pm.Model() as model:
alpha = pm.Normal("alpha", mu=0, sigma=10)
beta = pm.Normal("beta", mu=0, sigma=1)
e = pm.HalfCauchy("epsilon", 5)
mu = pm.Deterministic("mu", alpha + beta * x) # 確率的に表現するならば mu = pm.Nomal("mu", mu=alpha + beta * x, sd=e, observed=y)
y_pred = pm.Normal("y_pred", mu=mu, sigma=e, observed=y)
step = pm.Metropolis()
trace = pm.sample(10000, step=step, chains=1, cores=1)
trace_n = trace # TODO trace[1000:] でバーンすべきだが、KeyError: Get item by key. slice(1000, None, None) になる
az.plot_trace(trace_n)
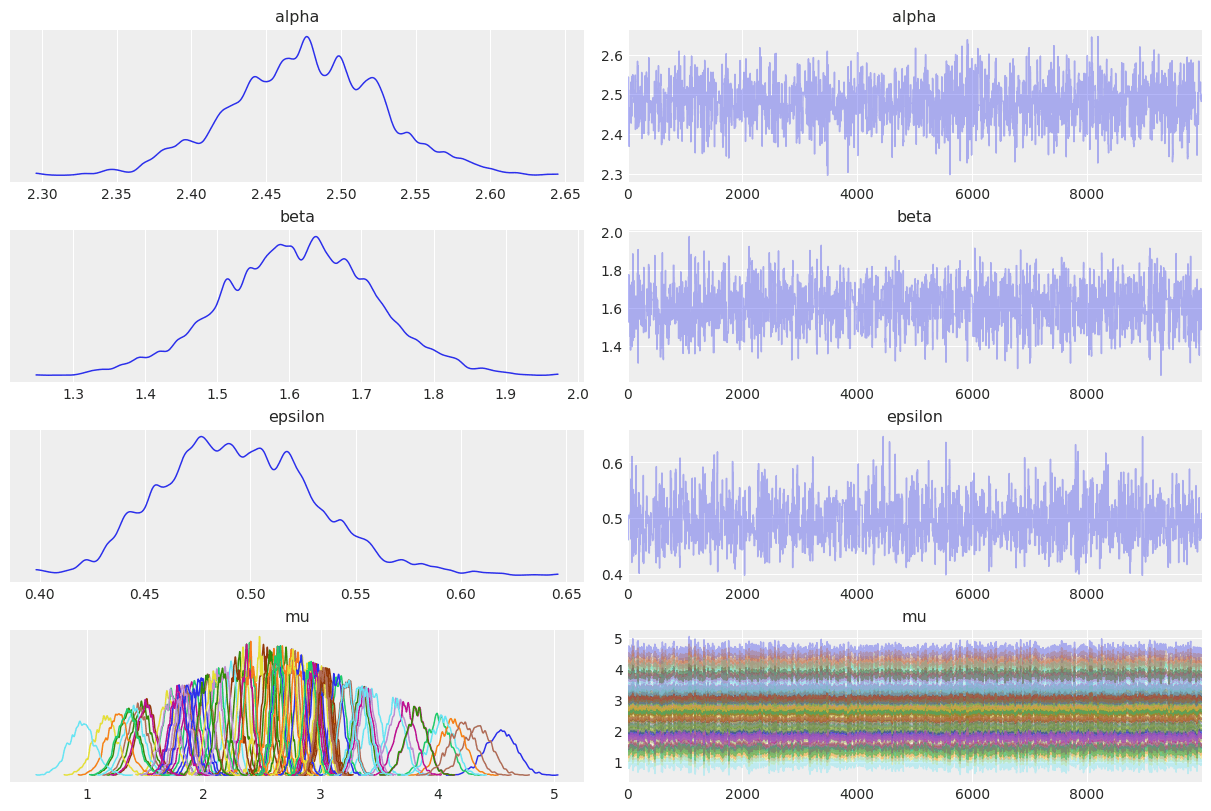
この結果で、もしも
今回は値も真値(
# 自己相関を可視化
az.plot_autocorr(trace_n, var_names=["alpha", "beta", "epsilon"])

自己相関が高い場合、
# aとbの事後分布の相関を可視化
sns.kdeplot(x=trace_n["posterior"]["alpha"][0], y=trace_n["posterior"]["beta"][0])
自己相関がある場合、KDEの図は斜めになる。
線形回帰で問題になる自己相関の問題に取り組む前にポイントを整理する。
- 最小二乗では回帰直線がデータの平均値を通るという制約がある
- ベイジアンでは厳密に平均を通る必要はなく、強い事前分布を仮定すればかなり離れた直線を描くこともできる
- どちらにせよ、自己相関は規定された点の周りを回転する回帰直線と関連している(?)
この問題を解決する方法として次の2点に手を入れる。
- 実行前のデータ標準化(Zスコア化)
- NUTSサンプラーの使用
# NUTSサンプラーでベイズ推定する
N = 100
a_real = 2.5
b_real = 1.5
e_real = np.random.normal(0, 0.5, N)
x = np.random.normal(0, 0.5, N)
y_real = a_real + b_real * x
y = y_real + e_real
# x = (x - np.mean(x))/np.std(x)
# y = (y - np.mean(y))/np.std(y)
plt.scatter(x, y)
plt.plot(x, y_real)
with pm.Model() as model:
alpha = pm.Normal("alpha", mu=0, sigma=10)
beta = pm.Normal("beta", mu=0, sigma=1)
e = pm.HalfCauchy("epsilon", 5)
mu = pm.Deterministic("mu", alpha + beta * x)
y_pred = pm.Normal("y_pred", mu=mu, sigma=e, observed=y)
step = pm.NUTS()
trace = pm.sample(10000, step=step, chains=1, cores=1)
trace_n = trace
az.plot_trace(trace_n)


# {a, b}の事後分布を用いて、回帰直線の事後予測分布を可視化
plt.scatter(x, y)
trace_post_a = trace_n.posterior["alpha"].values.reshape(-1) # shape [1000]
trace_post_b = trace_n.posterior["beta"].values.reshape(-1) # shape [1000]
idx = range(0, len(trace_post_a), 10) # 事後分布をx=10間隔で取ってくる
# shape [1000] * [100, 1000] = [100, 1000]
plt.plot(x, trace_post_a[idx] + trace_post_b[idx] * np.stack(x for _ in trace_post_a[idx]).transpose(1,0), c="b", alpha=0.01)
plt.plot(x, np.mean(trace_post_a)+np.mean(trace_post_b)*x, c="r")

# 決定的に定義したmuから、最高事後密度(HPD)を可視化
plt.scatter(x, y)
plt.plot(x, np.mean(trace_post_a)+np.mean(trace_post_b)*x, c="r")
idx = np.argsort(x)
trace_post_mu = trace_n.posterior["mu"] # [1, sample_size, n_data]
sig = pm.hdi(trace_n.posterior, hdi_prob=0.50)["mu"][idx] # [n_data, 2]
plt.fill_between(x[idx], sig[:,0], sig[:,1], color="b", alpha=0.50)

# 事後分布からyをサンプルして、その最高事後密度(HPD)を可視化
plt.scatter(x, y)
plt.plot(x, np.mean(trace_post_a)+np.mean(trace_post_b)*x, c="r")
idx = np.argsort(x)
ppc = pm.sample_posterior_predictive(trace_n, model=model) # attr: ["posterior_predictive", "observed_data"]
sig090 = pm.hdi(ppc.posterior_predictive, hdi_prob=0.10)["y_pred"][idx]
sig050 = pm.hdi(ppc.posterior_predictive, hdi_prob=0.50)["y_pred"][idx]
plt.fill_between(x[idx], sig050[:,0], sig050[:,1], color="b", alpha=0.50)
plt.fill_between(x[idx], sig090[:,0], sig090[:,1], color="r", alpha=0.50)

ピアソンの相関係数 r
相関係数はしばしば回帰直線の傾きと同一視されるが、必ずしも等価ではない。
(等価なのはデータが標準化されている場合などがある。)
決定係数 R^2
従属変数の分散に占める、独立変数から予測される分散の比率。
回帰直線の傾きと相関係数の関係式から求める方法と、最小二乗法と関係した導出方法がある。
# 線形回帰により決定係数 rb rss を求める
N = 100
alpha_real = 2.5
beta_real = 0.9
epsiron_real = 0.5
eps = np.random.normal(0, epsiron_real, size=N)
x = np.random.normal(10, 1, N)
y_real = alpha_real + beta_real * x
y = y_real + eps
with pm.Model() as model_n:
alpha = pm.Normal("alpha", mu=0, sigma=10)
beta = pm.Normal("beta", mu=0, sigma=1)
epsilon = pm.HalfCauchy("epsilon", 5)
mu = alpha + beta * x
y_pred = pm.Normal("y_pred", mu=mu, sigma=epsilon, observed=y)
rb = pm.Deterministic("rb", (beta * x.std() / y.std()) ** 2) # 回帰直線の傾きから決定係数を求める
ss_reg = pm.math.sum((mu - y.mean()) ** 2) # 回帰直線とデータの平均値との散らばりを示す測度 ∝ モデルの分散
ss_tot = pm.math.sum((y - y.mean()) ** 2) # 予測変数の分散
rrs = pm.Deterministic("rss", ss_reg/ss_tot) # 回帰直線の傾きから決定係数を求める
start = pm.find_MAP()
step = pm.NUTS()
trace_n = pm.sample(2000, step=step, initvals=start, chains=2, cores=2)
az.plot_trace(trace_n)
az.plot_autocorr(trace_n, var_names=["alpha", "beta", "epsilon", "rb", "rss"], combined=True)
az.summary(trace_n, var_names=["alpha", "beta", "epsilon", "rb", "rss"])
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
alpha 2.186 0.583 1.052 3.246 0.018 0.013 1098.0 1152.0 1.0
beta 0.930 0.057 0.828 1.044 0.002 0.001 1092.0 1225.0 1.0
epsilon 0.524 0.037 0.458 0.596 0.001 0.001 2011.0 1740.0 1.0
rb 0.731 0.090 0.559 0.898 0.003 0.002 1092.0 1225.0 1.0
rss 0.734 0.090 0.578 0.917 0.003 0.002 1094.0 1212.0 1.0


多変量正規分布からのピアソンの相関係数
共分散行列は各変数の分散とその相関係数で表現できる。
この推定には3つの方法がある。
- 事前分布にWishart分布 を用いる: これは多変量正規分布の共分散行列の逆行列(つまり精度)の対する共役事前分布で、ガンマ分布の高次元への一般化である。
- 事前分布にLKJ分布を用いる: 相関行列に対する事前分布で、共分散行列に対するものではないが、相関を考えるときに役立つ。
-
σ_i, σ_j, ρ
# 回帰問題から2変数の共分散行列を作り、相関係数rhoを示す
N = 100
alpha_real = 2.5
beta_real = 0.9
epsiron_real = 0.5
eps = np.random.normal(0, epsiron_real, size=N)
x = np.random.normal(10, 1, N)
y_real = alpha_real + beta_real * x
y = y_real + eps
data = np.stack([x, y]).transpose()
with pm.Model() as pearson_model:
mu = pm.Normal("mu", mu=data.mean(0), sigma=10, shape=2)
sigma_1 = pm.HalfNormal("sigma_1", 10)
sigma_2 = pm.HalfNormal("sigma_2", 10)
rho = pm.Uniform("rho", -1, 1)
cov = pm.math.stack([[sigma_1**2, rho*sigma_1*sigma_2], [rho*sigma_2*sigma_1, sigma_2**2]])
y_pred = pm.MvNormal("y_pred", mu=mu, cov=cov, observed=data)
start = pm.find_MAP()
step = pm.NUTS()
trace_p = trace_n = pm.sample(1000, step=step, initvals=start, chains=2, cores=1)
az.plot_trace(trace_n)
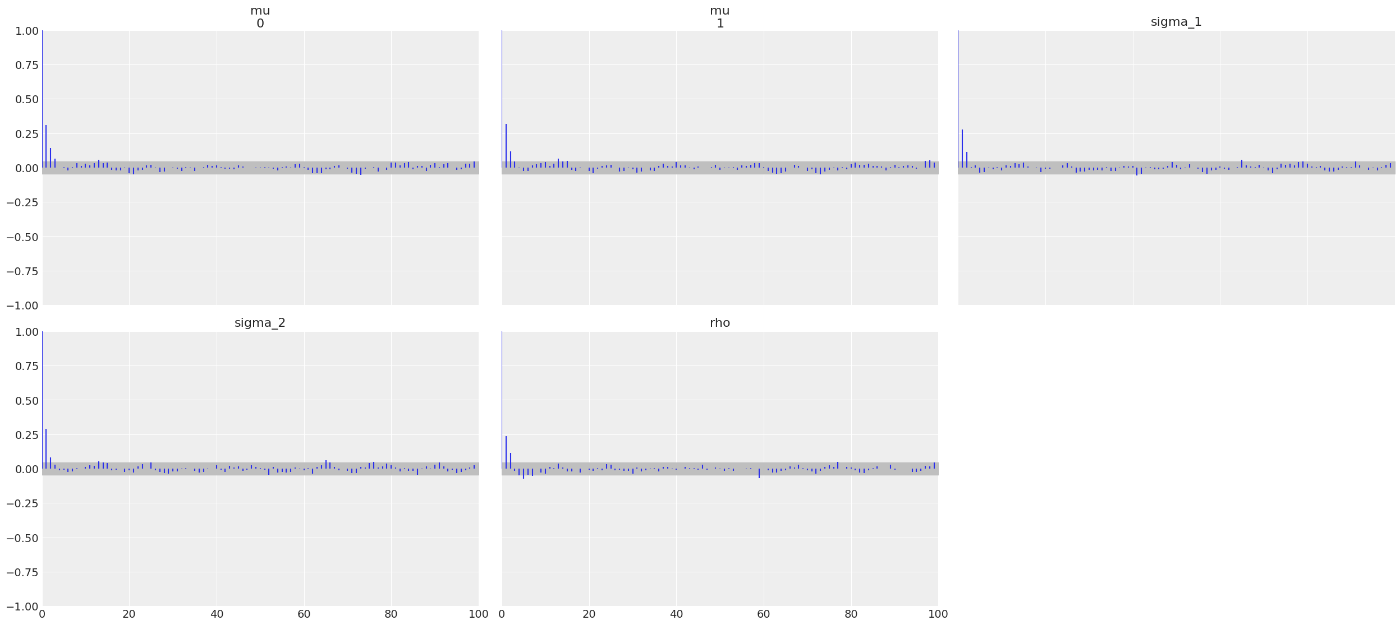
az.plot_autocorr(trace_n, var_names=["mu", "sigma_1", "sigma_2", "rho"], combined=True)
az.summary(trace_n, var_names=["mu", "sigma_1", "sigma_2", "rho"])
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
mu[0] 10.118 0.122 9.877 10.328 0.004 0.003 989.0 1059.0 1.0
mu[1] 11.568 0.129 11.323 11.797 0.004 0.003 1031.0 1137.0 1.0
sigma_1 1.169 0.083 1.014 1.323 0.002 0.002 1132.0 1239.0 1.0
sigma_2 1.212 0.087 1.053 1.379 0.003 0.002 1126.0 1221.0 1.0
rho 0.885 0.022 0.845 0.924 0.001 0.000 1218.0 1202.0 1.0

2. ロバスト線形回帰
外れ値がある場合は通常の正規分布よりT分布を用いたほうがロバストな回帰が可能になる。
Anscombeデータセットを用いて外れ値が含まれるデータの線形回帰を試してみる。
まず通常のガウス分布を用いた回帰を行い、次にT分布による回帰を行う。
# anscombeデータセットの3(カルテット)と、ガウス分布による線形回帰
anscombe = sns.load_dataset("anscombe")
x3 = anscombe[anscombe.dataset == "III"]["x"].values
y3 = anscombe[anscombe.dataset == "III"]["y"].values
with pm.Model() as model_t:
alpha = pm.Normal("alpha", mu=0, sigma=10)
beta = pm.Normal("beta", mu=0, sigma=10)
epsilon = pm.HalfCauchy("epsilon", 5)
mu = pm.Deterministic("mu", alpha + beta * x3)
y_pred = pm.Normal("y_pred", mu=mu, sigma=epsilon, observed=y3)
start = pm.find_MAP()
step = pm.NUTS()
trace_n = pm.sample(1000, step=step, initvals=start, chains=2, cores=1)
az.plot_trace(trace_n)
az.plot_autocorr(trace_n, var_names=["alpha", "beta", "epsilon", "mu"], combined=True)
az.summary(trace_n, var_names=["alpha", "beta", "epsilon", "mu"])
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
alpha 2.862 1.314 0.362 5.314 0.056 0.041 551.0 508.0 1.0
beta 0.514 0.138 0.254 0.771 0.006 0.004 546.0 591.0 1.0
epsilon 1.438 0.400 0.849 2.187 0.017 0.012 618.0 656.0 1.0
mu[0] 7.997 0.482 7.120 8.984 0.012 0.008 1672.0 1101.0 1.0
...
mu[10] 5.430 0.710 4.128 6.755 0.027 0.020 687.0 626.0 1.0


idx = np.argsort(x3)
trace_post_a = trace_n.posterior["alpha"].values.reshape(-1)
trace_post_b = trace_n.posterior["beta"].values.reshape(-1)
sig = pm.hdi(trace_n.posterior, hdi_prob=0.50)["mu"][idx]
plt.scatter(x3, y3)
plt.plot(x3, np.mean(trace_post_a[idx])+np.mean(trace_post_b[idx])*x3, c="r")
plt.fill_between(x3[idx], sig[:,0], sig[:,1], color="b", alpha=0.50)
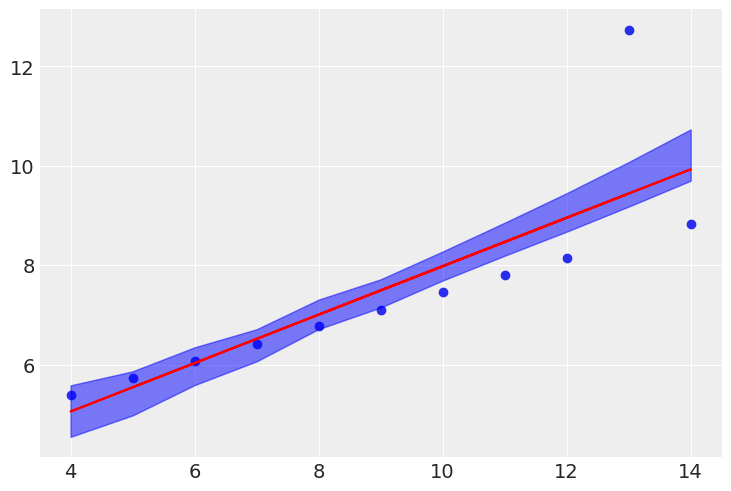
# anscombeデータセットの3(カルテット)と、T分布による線形回帰
anscombe = sns.load_dataset("anscombe")
x3 = anscombe[anscombe.dataset == "III"]["x"].values
y3 = anscombe[anscombe.dataset == "III"]["y"].values
with pm.Model() as model_t:
alpha = pm.Normal("alpha", mu=0, sigma=10)
beta = pm.Normal("beta", mu=0, sigma=10)
epsilon = pm.HalfCauchy("epsilon", 5)
nu = pm.Deterministic("nu", pm.Exponential("nu_", 1/29)+1) # nuは事前分布Gamma(mu=20,sigma=15)が普通だが、極端な外れ値のデータにはシフトした指数分布を使う
mu = pm.Deterministic("mu", alpha + beta * x3)
y_pred = pm.StudentT("y_pred", mu=mu, sigma=epsilon, nu=nu, observed=y3)
start = pm.find_MAP()
step = pm.NUTS()
trace_n = pm.sample(1000, step=step, initvals=start, chains=2, cores=1)
az.plot_trace(trace_n)
az.plot_autocorr(trace_n, var_names=["alpha", "beta", "epsilon", "nu", "mu"], combined=True)
az.summary(trace_n, var_names=["alpha", "beta", "epsilon", "nu", "mu"])
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
alpha 4.007 0.004 3.998 4.014 0.000 0.000 625.0 772.0 1.0
beta 0.345 0.000 0.345 0.346 0.000 0.000 633.0 707.0 1.0
epsilon 0.003 0.002 0.001 0.006 0.000 0.000 526.0 258.0 1.0
nu 1.205 0.192 1.000 1.567 0.007 0.005 636.0 702.0 1.0
mu[0] 7.460 0.001 7.456 7.462 0.000 0.000 1842.0 1219.0 1.0
...
mu[10] 5.733 0.002 5.729 5.737 0.000 0.000 715.0 1057.0 1.0

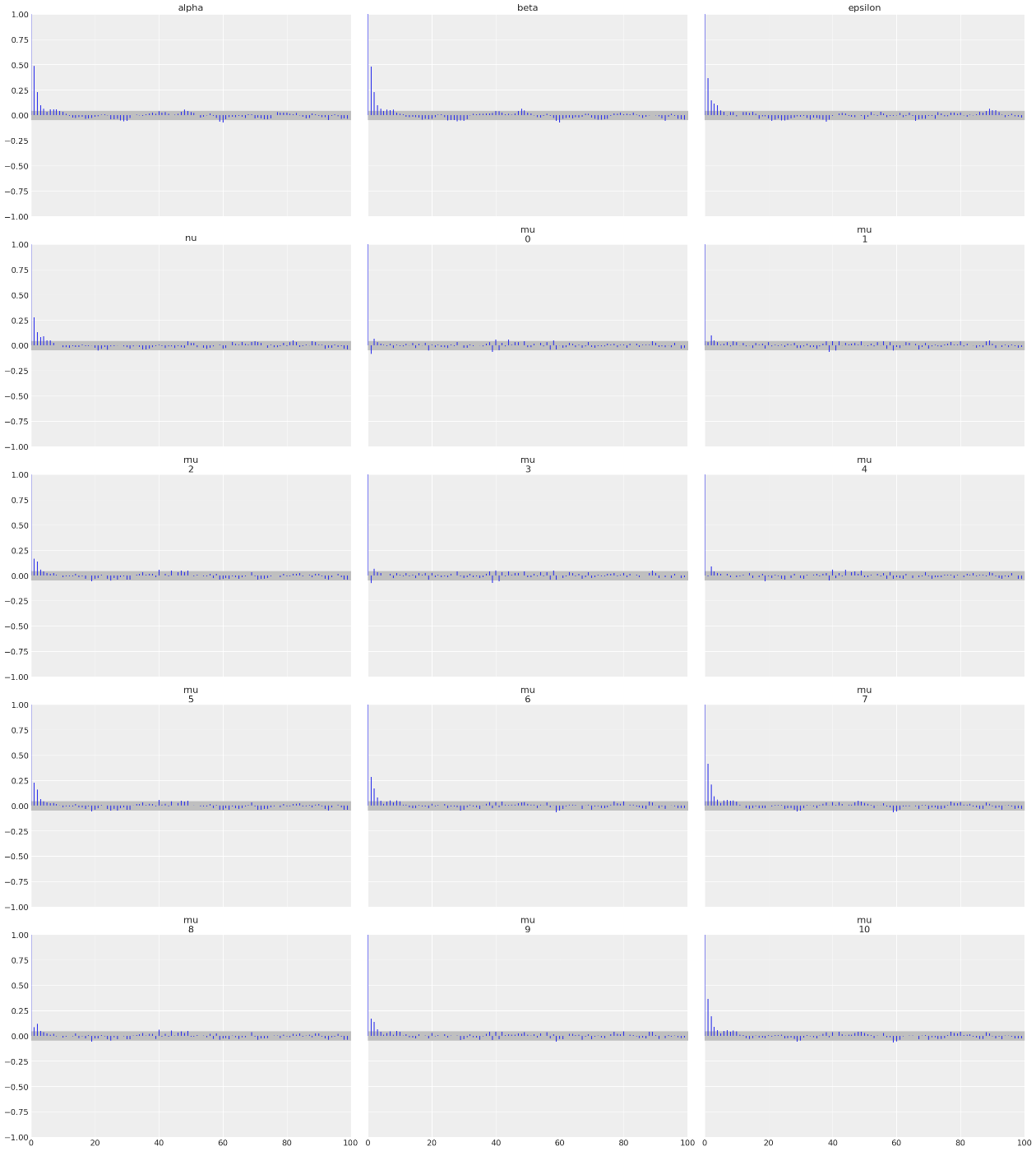
idx = np.argsort(x3)
trace_post_a = trace_n.posterior["alpha"].values.reshape(-1)
trace_post_b = trace_n.posterior["beta"].values.reshape(-1)
plt.scatter(x3, y3)
plt.plot(x3, np.mean(trace_post_a[idx])+np.mean(trace_post_b[idx])*x3, c="r")
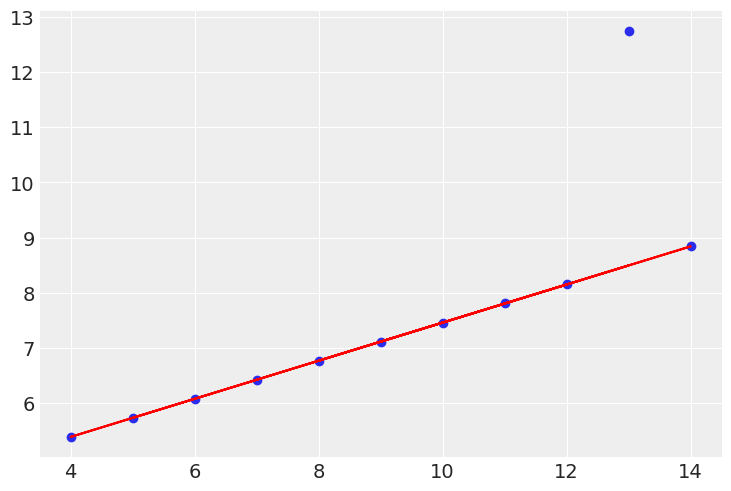
3. 階層線形回帰
個々のグループレベルの推定やグループ全体の推定ではハイパー事前分布を用いてこれを行うことができる。
例えば、データセットの中にデータ点が1つしかないようなグループがあるデータを使った線形回帰を行う。
階層モデルを作ることで他データの情報を共有する事ができ、データがスパースなのものに対してもグループ全体で情報を補うことができる。
# 複数のデータをもつグループを作成
N = 20
M = 8
idx = np.repeat(range(M-1), N)
idx = np.append(idx, 7)
alpha_real = np.random.normal(2.5, 0.5, size=M)
beta_real = np.random.normal(0.9, 0.5, size=M)
eps_real = np.random.normal(0, 0.5, size=len(idx))
print(alpha_real)
print(beta_real)
x_m = np.random.normal(10, 1, len(idx))
y_m = np.zeros(len(idx))
y_m = alpha_real[idx] + beta_real[idx] * x_m + eps_real
plt.figure(figsize=(18,8))
j = 0
k = N
for i in range(M):
plt.subplot(2, 4, i+1)
plt.scatter(x_m[j:k], y_m[j:k])
j += N
k += N
plt.tight_layout()
[3.24896561 2.96662634 2.20161262 1.29777438 2.22663501 2.50655879
2.42185945 1.88404336]
[0.83314726 0.82485358 1.02193226 0.47892426 2.21610795 0.63039093
1.03172176 1.14515431]

# ハイパー事前分布として事前分布のパラメータに事前分布を仮定した線形回帰
with pm.Model() as model_h:
alpha_mu = pm.Normal("alpha_mu", mu=0, sigma=10)
alpha_sig = pm.HalfNormal("alpha_sig", 10)
alpha = pm.Normal("alpha", mu=alpha_mu, sigma=alpha_sig, shape=M)
beta_mu = pm.Normal("beta_mu", mu=0, sigma=10)
beta_sig = pm.HalfNormal("beta_sig", 10)
beta = pm.Normal("beta", mu=beta_mu, sigma=beta_sig, shape=M)
epsilon = pm.HalfCauchy("epsilon", 5)
y_pred = pm.Normal("y_pred", mu=alpha[idx] + beta[idx] * x_m, sigma=epsilon, observed=y_m)
trace_n = pm.sample(1000, chains=2, cores=1)
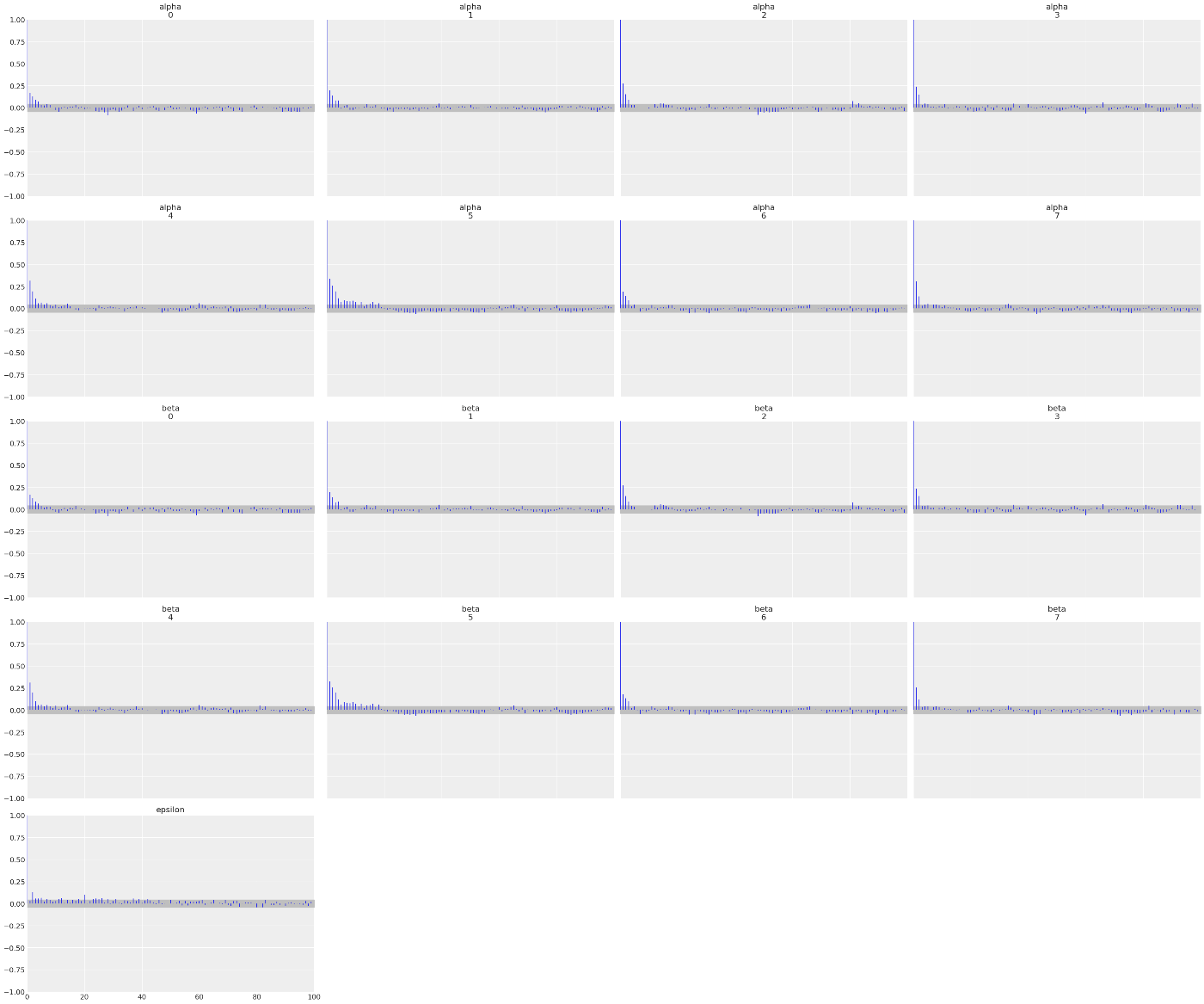
az.plot_trace(trace_n)
az.plot_autocorr(trace_n, var_names=["alpha", "beta", "epsilon"], combined=True)
az.summary(trace_n, var_names=["alpha", "beta", "epsilon"])

# 回帰直線を可視化
plt.figure(figsize=(18,8))
j = 0
k = N
x_range = np.linspace(x_m.min(), x_m.max(), 10)
for i in range(M):
plt.subplot(2, 4, i+1)
plt.scatter(x_m[j:k], y_m[j:k])
trace_post_a = trace_n.posterior["alpha"].values[:,i].reshape(-1)
trace_post_b = trace_n.posterior["beta"].values[:,i].reshape(-1)
plt.plot(x_range, alpha_real[i] + beta_real[i] * x_range, c="b")
plt.plot(x_range, trace_post_a.mean() + trace_post_b.mean() * x_range, c="r")
j += N
k += N
plt.tight_layout()

(上手くいってないかも...)
4. 多項式回帰
線形回帰モデルを用いて曲線をfitしたい。
多項式回帰はfitするパラメータβが線形であり、これも線形回帰モデルである。
今回は放物線を回帰する。
# 放物線の観測値を作り、これを近似する
anscombe = sns.load_dataset("anscombe")
x2 = anscombe[anscombe.dataset == "II"]["x"].values
y2_real = anscombe[anscombe.dataset == "II"]["y"].values
y2 = y2_real + np.random.normal(0, 0.3, size=len(y2_real))
idx = np.argsort(x2)
x2, y2, y2_real = x2[idx], y2[idx], y2_real[idx]
with pm.Model() as model_poly:
beta0 = pm.Normal("beta0", mu=0, sigma=10)
beta1 = pm.Normal("beta1", mu=0, sigma=1)
beta2 = pm.Normal("beta2", mu=0, sigma=1)
epsilon = pm.HalfCauchy("epsilon", 5)
mu = pm.Deterministic("mu", beta0 + beta1 * x2 + beta2 * x2**2)
y_pred = pm.Normal("y_pred", mu=mu, sigma=epsilon, observed=y2)
trace_poly = pm.sample(2000, chains=2, cores=1)
az.plot_trace(trace_poly)
az.plot_autocorr(trace_poly, var_names=["beta0", "beta1", "beta2", "epsilon", "mu"], combined=True)
az.summary(trace_poly, var_names=["beta0", "beta1", "beta2", "epsilon", "mu"])


trace_post_b0 = trace_poly.posterior["beta0"].values
trace_post_b1 = trace_poly.posterior["beta1"].values
trace_post_b2 = trace_poly.posterior["beta2"].values
plt.scatter(x2, y2)
plt.plot(x2, y2_real, c="b")
plt.plot(x2, trace_post_b0.mean() + trace_post_b1.mean() * x2 + trace_post_b2.mean() * x2**2, c="r")

多項式回帰の解釈の問題はパラメータの解釈にある。
変数xの単位あたりのyの変化量を知りたい時、β1のみのチェックするだけでは足りないということである。1次項以外にも2次項以降が影響を与えるため、多くの変数を見る必要がある。
また、パラメータは所詮fitする回帰曲線のパラメータであり、データを生成する隠れた過程を理解できるものではない。
そして、無限に高次な多項式回帰はノイズにもfitするため過学習しやすい。
実用上は2,3次以上の多項式回帰は使いにくい。
5. 重回帰
複数の独立変数から1つの従属変数を回帰する。
# データを用意する
N = 100
alpha_real = 2.5
beta_real = [0.9, 1.5]
eps_real = np.random.normal(0, 0.5, size=N)
x = np.array([np.random.normal(10, 1, N), np.random.normal(2, 1.5, N)])
x_mean = x.mean(axis=1, keepdims=True)
x_centered = x - x_mean
y = alpha_real + np.dot(beta_real, x) + eps_real
print(x.shape, y.shape)
plt.Figure(figsize=(10,10))
plt.subplot(2,2,1)
plt.scatter(x[0], y) # 左上
plt.subplot(2,2,2)
plt.scatter(x[1], y) # 右上
plt.subplot(2,2,3)
plt.scatter(x[0], x[1]) # 左下

# 線形重回帰を実行する
with pm.Model() as model_mlr:
alpha_tmp = pm.Normal("alpha_tmp", mu=0, sigma=10)
beta = pm.Normal("beta", mu=0, sigma=1, shape=2)
epsilon = pm.HalfCauchy("epsilon", 5)
mu = alpha_tmp + pm.math.dot(beta, x_centered)
alpha = pm.Deterministic("alpha", alpha_tmp - pm.math.dot(beta, x_mean))
y_pred = pm.Normal("y_pred", mu=mu, sigma=epsilon, observed=y)
trace_mlr = pm.sample(5000, chains=2, cores=1)
print("alpha = ", alpha_real, "pred = ", trace_mlr.posterior["alpha"].values.mean())
print("beta = ", beta_real, "pred = ", trace_mlr.posterior["beta"].values[:,:,0].mean(), trace_mlr.posterior["beta"].values[:,:,1].mean())
az.plot_trace(trace_mlr)
az.plot_autocorr(trace_mlr, var_names=["beta", "alpha", "alpha_tmp", "epsilon"], combined=True)
az.summary(trace_mlr, var_names=["beta", "alpha", "alpha_tmp", "epsilon"])
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
beta[0] 0.881 0.052 0.783 0.978 0.000 0.000 14531.0 8763.0 1.0
beta[1] 1.464 0.030 1.407 1.518 0.000 0.000 13702.0 8169.0 1.0
alpha[0] 2.744 0.525 1.731 3.701 0.004 0.003 14585.0 8764.0 1.0
alpha_tmp 14.426 0.052 14.328 14.521 0.000 0.000 16128.0 7876.0 1.0
epsilon 0.521 0.038 0.454 0.596 0.000 0.000 13918.0 8072.0 1.0

この結果を見る通り、α = 2.5に対し推定平均2.7、β = [0.9, 1.5]に対し推定平均[0.88, 1.46]となり、推定できている。
交絡変数
次の問題設定では、
# 交絡因子x_1を媒介するデータセット
N = 100
x_1 = np.random.normal(0, 1, size=N)
x_2 = x_1 + np.random.normal(size=N, scale=1.0)
y = x_1 + np.random.normal(0, 0.5, size=N)
x = np.vstack([x_1, x_2])
print(x.shape, y.shape)
plt.Figure(figsize=(10,10))
plt.subplot(2,2,1)
plt.scatter(x[0], y) # 左上
plt.subplot(2,2,2)
plt.scatter(x[1], y) # 右上
plt.subplot(2,2,3)
plt.scatter(x[0], x[1]) # 左下
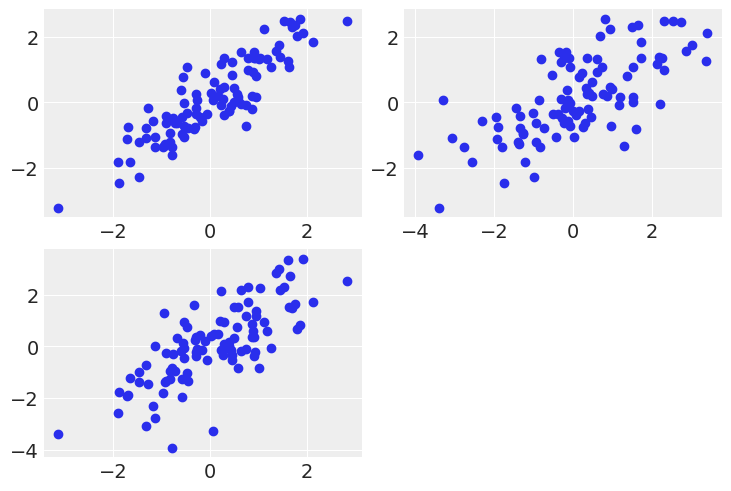
with pm.Model() as model_red:
alpha = pm.Normal("alpha", mu=0, sigma=1)
beta = pm.Normal("beta", mu=0, sigma=10, shape=2)
epsilon = pm.HalfCauchy("epsilon", 5)
mu = alpha + pm.math.dot(beta, x)
y_pred = pm.Normal("y_pred", mu=mu, sigma=epsilon, observed=y)
trace_red = pm.sample(5000, chains=2, cores=1)
az.plot_trace(trace_red)
az.plot_autocorr(trace_red, var_names=["beta", "alpha", "epsilon"], combined=True)
az.summary(trace_red, var_names=["beta", "alpha", "epsilon"])
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
beta[0] 1.386 0.580 0.325 2.513 0.009 0.006 4288.0 4638.0 1.0
beta[1] -0.341 0.582 -1.462 0.738 0.009 0.006 4276.0 4655.0 1.0
alpha 0.038 0.054 -0.058 0.143 0.001 0.001 6676.0 6190.0 1.0
epsilon 0.540 0.040 0.469 0.616 0.001 0.000 5927.0 5424.0 1.0


このとき
多重共線性
2つの変数が非常に高い相関を持っている場合の重回帰はどうなるか。
# x_1とx_2が非常に相関が高いデータセット
N = 100
x_1 = np.random.normal(0, 1, size=N)
x_2 = x_1 + np.random.normal(size=N, scale=0.1)
y = x_1 + np.random.normal(0, 0.5, size=N)
x = np.vstack([x_1, x_2])
print(x.shape, y.shape)
plt.Figure(figsize=(10,10))
plt.subplot(2,2,1)
plt.scatter(x[0], y) # 左上
plt.subplot(2,2,2)
plt.scatter(x[1], y) # 右上
plt.subplot(2,2,3)
plt.scatter(x[0], x[1]) # 左下

with pm.Model() as model_red:
alpha = pm.Normal("alpha", mu=0, sigma=1)
beta = pm.Normal("beta", mu=0, sigma=10, shape=2)
epsilon = pm.HalfCauchy("epsilon", 5)
mu = alpha + pm.math.dot(beta, x)
y_pred = pm.Normal("y_pred", mu=mu, sigma=epsilon, observed=y)
trace_red = pm.sample(5000, chains=2, cores=1)
az.plot_trace(trace_red)
az.plot_autocorr(trace_red, var_names=["beta", "alpha", "epsilon"], combined=True)
az.summary(trace_red, var_names=["beta", "alpha", "epsilon"])
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
beta[0] 1.392 0.571 0.339 2.476 0.009 0.007 3747.0 4156.0 1.0
beta[1] -0.346 0.574 -1.465 0.689 0.009 0.007 3731.0 4276.0 1.0
alpha 0.037 0.055 -0.065 0.139 0.001 0.001 6786.0 5720.0 1.0
epsilon 0.539 0.039 0.466 0.612 0.001 0.000 5404.0 5382.0 1.0


また、どちらかの係数が小さくなるという相関も発生する。式でいうと、
こうなるとβは別々の値ではなくなり、さらにデータが影響を及ぼさなくなって
# HPDの確認
az.plot_posterior(trace_red, ref_val=0, var_names=["beta"])

以上の話から分かる通り、モデルが良い予測をしていたとしても、各係数から説明性を得ようとしたときに相関が高いデータでは良くない場合があることが確かめられる。
相関が高いデータを扱う時、次のことが勧められる。
- 相関が高い係数をどちらか片方削除する。
- 相関が高い係数をPCAなどにより1つの変数にまとめる(ただし主成分の軸が出てくるので解釈には不向き)。
- 正則化事前分布 など強い制約のある事前分布を与えて、自身の知識をモデルに持たせて相関が高い係数を束縛する。
変数のマスキング効果: 独立変数と従属変数との間に正の相関があり、逆に他の独立変数と従属変数との間では負の相関がある場合、どちらかを削除してしまうと本来の効果を過小に推定してしまう。
相互作用の追加(interaction): 独立変数
感想
線形回帰の話題ということもあり新知識は少なかったが、コードを追うことでPyMC3のコードをPyMC5へ読み替えるドリルとして活用できた。
メトロポリスサンプラーより明らかにNUTSサンプラーのほうが良かった結果となった。
PyMC5自体の本家チュートリアルをまだ読んでいないので、できればそっちも早く頭に入れておきたい。PyMC5を使うにはarvizとxarrayをある程度弄れたほうが良いので、そっちも...
Discussion