Zenn
🙄

Bayesian Analysis with PyMC 勉強ノート 5 分類モデル

2024/01/08に公開
統計
pymc
tech

Osvaldo Martin 著, 金子武久 訳
Pythonによるベイズ統計モデリング (Bayesian Analysis with Python)
2018-06-26
https://www.kyoritsu-pub.co.jp/book/b10003944.html

Christopher M. Bishop 著, 元田浩 栗田多喜夫 樋口知之 松本裕治 村田昇 監訳
パターン認識と機械学習 ベイズ理論による統計的予測 (Pattern Recognition and Machine Learning)
2012-01-20
https://www.maruzen-publishing.co.jp/item/?book_no=294524

Pythonによるベイズ統計モデリングを読んだので学習メモを整理します。学習中のノートなので正確ではないかもしれません。使われているコードをPyMC3からPyMC5に書き直しました。
また、せっかくなのでPRMLの本を参照しながら読むことにしました。式の文字の扱いなどはPRML風になるよう頭に収めようと思っています。

https://www.kyoritsu-pub.co.jp/book/b10003944.html

https://www.pymc.io/welcome.html

ロジスティック回帰

次のライブラリを使用する。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

import pymc as pm
import arviz as az

az.style.use("arviz-darkgrid")

0. 線形回帰を題材にしたこれまでの復習

教師データtを決定的な関数y(\bold{x},\bold{w})と加法性ガウスノイズε \sim \mathcal{N}(ε|0, β^{-1})の和で表す時、以下の式で与えられる。

t = y(\bold{x},\bold{w}) \\ p(t|\bold{x},\bold{w}, β) = \mathcal{N}(t|y(\bold{x},\bold{w}), β^{-1})

ベイズ線形回帰を扱うと、通常の最尤推定による回帰モデルで起こる過学習を避け、モデルの複雑さを自動的に決定できる嬉しさがある。
MCMCを使える今回は代数計算による必要がないので、モデルパラメータ\bold{w}の事前分布が共役でなくても問題ない。
PRML3.3の例では、以下の設定の問題を解いている。

  • 単回帰モデルy(x,\bold{w}) = w_0 + w_1 x
  • f_{\texttt{real}}(x,\bold{a}) = a_0 + a_1 x ただし a_0 = -0.3, a_1 = 0.5 を生成元とする。
  • x_n \sim \mathcal{U}(x|y(-1, 1) によって観測した \{ x_n \} で f_{\texttt{real}}(x_n,\bold{a}) を評価
  • ε \sim \mathcal{N}(ε|0, 0.2^2) から観測した誤差を加えた t_n = x_n + ε を目標値(訓練データ) \{ t_n \} とする
  • \{ t_n \} から真のパラメータ \bold{a} を復元(推定)する
  • PRMLでは精度 β = (1/0.2)^2 は既知として扱うが、今回はこれも半コーシー分布から推定する
N = 20
a0_real = -0.3
a1_real = 0.5
e_real = np.random.normal(0, 0.2, N)  # loc: μ, scale: σ

x = np.random.uniform(-1.0, 1.0, N)
y_real = a0_real + a1_real * x
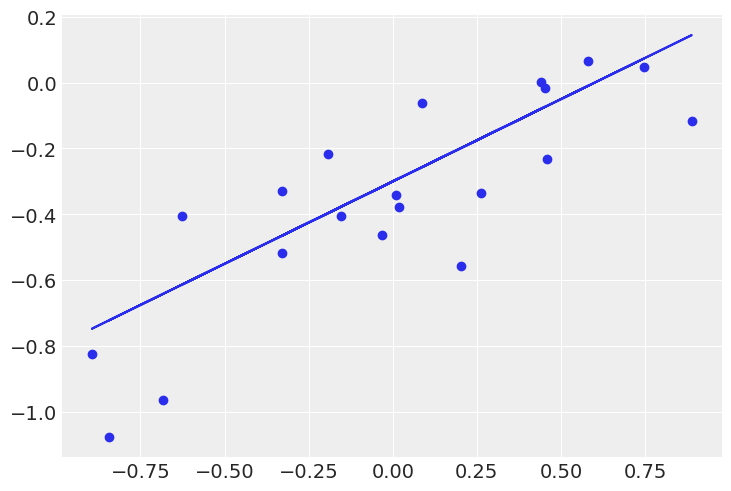
y = y_real + e_real

plt.plot(x, y_real)
plt.scatter(x, y)


with pm.Model() as model:
    w0 = pm.Normal("w0", mu=0, sigma=1)
    w1 = pm.Normal("w1", mu=0, sigma=1)
    e = pm.HalfCauchy("epsilon", 5)
    mu = pm.Deterministic("mu", w0 + w1 * x)
    y_pred = pm.Normal("y_pred", mu=mu, sigma=e, observed=y)

    trace = pm.sample(1000, chains=2, cores=1)

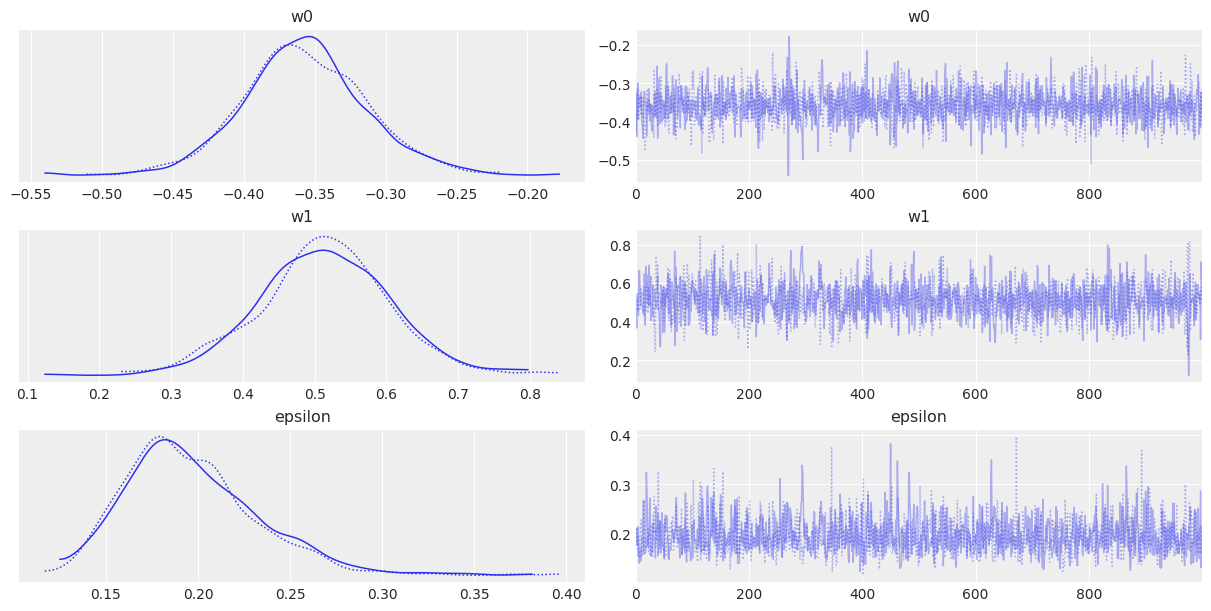
az.plot_trace(trace, var_names=["w0", "w1", "epsilon"])
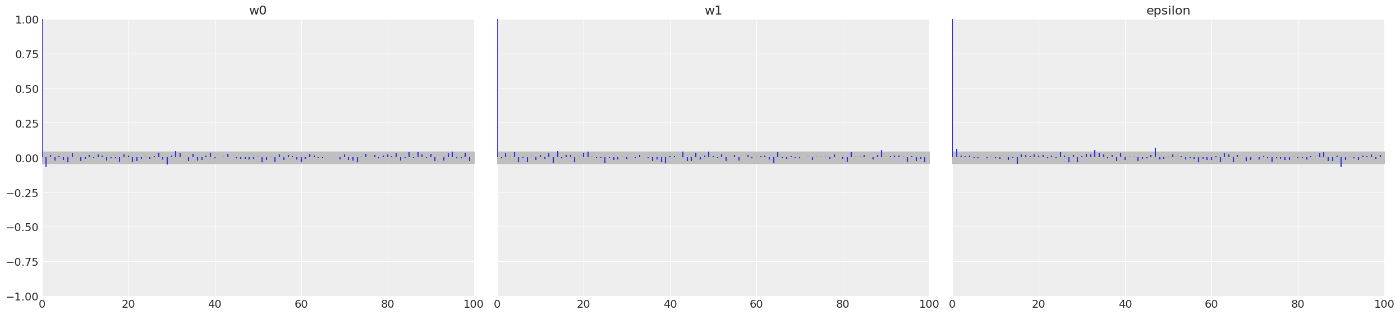
az.plot_autocorr(trace, var_names=["w0", "w1", "epsilon"], combined=True)
az.summary(trace, var_names=["w0", "w1", "epsilon"])
output
	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
w0	-0.357	0.043	-0.436	-0.273	0.001	0.001	2326.0	1482.0	1.0
w1	0.514	0.091	0.333	0.674	0.002	0.002	1921.0	1314.0	1.0
epsilon	0.197	0.036	0.136	0.262	0.001	0.001	1669.0	1042.0	1.0


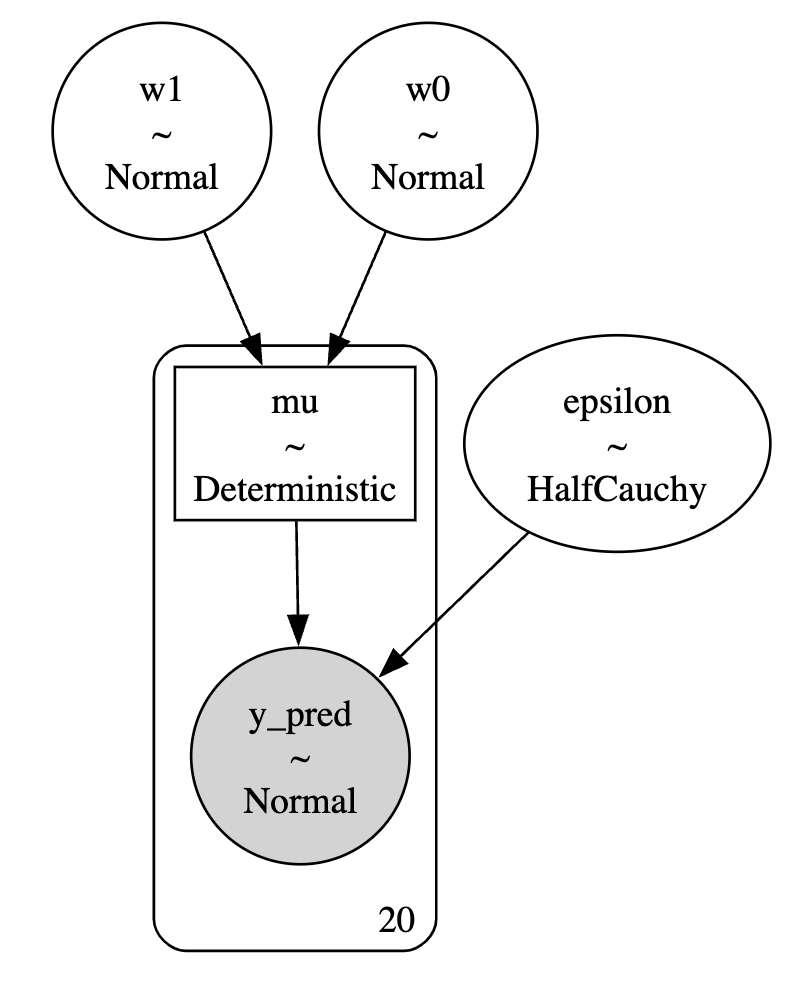
graphvizをインストールしてあると、グラフィカルモデルを可視化できる。

# brew install graphviz
# pip install graphviz
pm.model_to_graphviz(model=model)

a_0 = -0.3, a_1 = 0.5, β = (1/0.2)^2 に対して、それぞれのパラメータの事後分布の期待値はだいたい w_0 = -0.36, w1 = 0.51, β = (1/0.20)^2 となっており、かなり良く推定できている。

事前分布と事後分布について確認する。

# https://www.pymc.io/projects/docs/en/latest/api/generated/pymc.sampling.forward.sample_prior_predictive.html
# Sampling: [epsilon, w0, w1, y_pred]
myprior = pm.sample_prior_predictive(samples=50, model=model)
# Inference data with groups:
#    > prior
#    > prior_predictive
#    > observed_data

# https://www.pymc.io/projects/docs/en/latest/api/generated/pymc.sampling.forward.sample_posterior_predictive.html
# Sampling: [y_pred]
myposterior = pm.sample_posterior_predictive(trace, model=model)
# print(myposterior)
# Inference data with groups:
#    > posterior_predictive
#    > observed_data

sns.kdeplot(x=myprior.prior["w0"].values.reshape(-1), y=myprior.prior["w1"].values.reshape(-1), cmap=sns.light_palette("blue", as_cmap=True))
sns.kdeplot(x=trace.posterior["w0"].values.reshape(-1), y=trace.posterior["w1"].values.reshape(-1), cmap=sns.light_palette("red", as_cmap=True))
plt.xlim([-1.0, 1.0])
plt.ylim([-1.0, 1.0])
plt.show()

もともと広く適当に設定していた事前分布が、データ観測によって最適化された事後分布になったことがわかる。

予測分布

実際的にはパラメータそのものではなく新しい\bold{x}の値に対して予測されるtの分布がほしい。そのときは予測分布(predictive distribution)を評価すればよい。ガウス分布を仮定した場合は以下のように定義できる。

p(t | \bold{x}, \bold{t}, α, β) = \int p(t | \bold{x}, \bold{w}, β) p(\bold{w} | \bold{x}, \bold{t}, α, β) d\bold{w}

ただし

  • 目標変数の条件付き分布 p(t | \bold{x}, \bold{w}, β) = \mathcal{N}(t | y(\bold{x}, \bold{w}), β^{-1})
  • パラメータ \bold{w} の事後分布 p(\bold{w} | \bold{t}, α, β)
  • α, β はそれぞれパラメータの精度と目標変数の精度

MCMCで扱えば代数的に計算しなくても可視化できる。

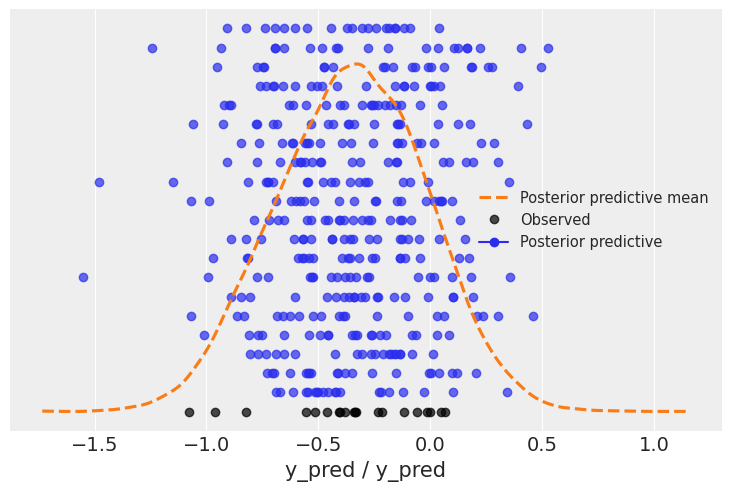
# y_predが観測データを再現できるか確認
# https://python.arviz.org/en/stable/api/generated/arviz.plot_ppc.html
az.plot_ppc(myposterior, num_pp_samples=20, kind="scatter")
plt.show()

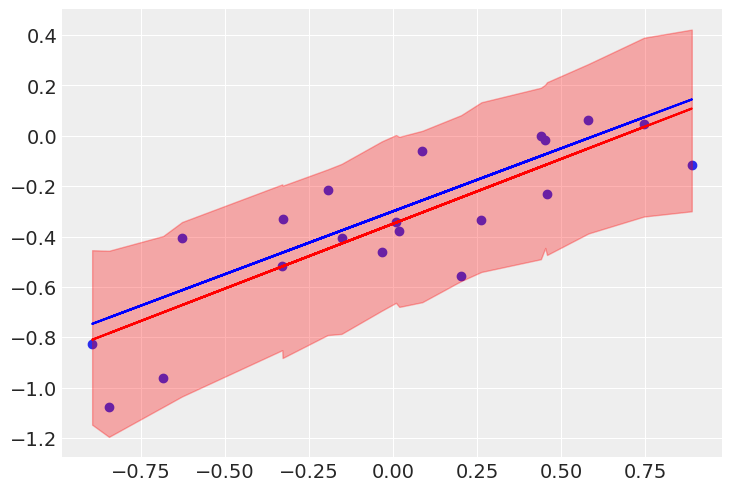
# 予測パラメータのサンプリングによるモデルの不確かさの可視化
idx = np.argsort(x)
post_w0 = trace.posterior["w0"].values.reshape(-1)
post_w1 = trace.posterior["w1"].values.reshape(-1)

sig = az.hdi(myposterior.posterior_predictive, hdi_prob=0.90)["y_pred"].values[idx]  # az.hdi(trace.posterior) -> <xarray.Dataset> [4(=w0+w1+eps+mu), draw]
plt.scatter(x, y)
plt.plot(x, np.mean(post_w0[idx])+np.mean(post_w1[idx])*x, c="r")  # 予測分布の期待値による回帰直線
plt.plot(x, a0_real + a1_real * x, c="b")  # データ生成元の直線
plt.fill_between(x[idx], y1=sig[:,0], y2=sig[:,1], color="r", alpha=0.30)  # 信頼区間
plt.show()

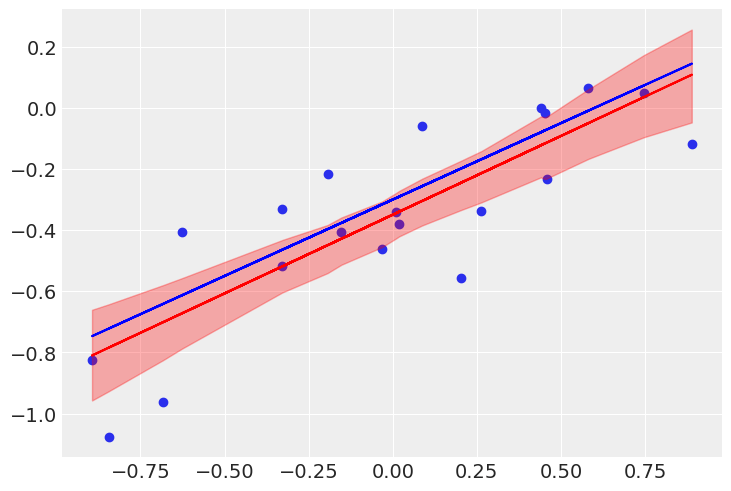
# 予測パラメータの最高密度区間(ベイズ信頼区間)によるモデルの不確かさの可視化
sig = az.hdi(trace.posterior, hdi_prob=0.90)["mu"].values[idx]  
plt.scatter(x, y)
plt.plot(x, np.mean(post_w0[idx])+np.mean(post_w1[idx])*x, c="r")
plt.plot(x, a0_real + a1_real * x, c="b")
plt.fill_between(x[idx], y1=sig[:,0], y2=sig[:,1], color="r", alpha=0.30)
plt.show()



逐次推論

[1] https://www.microsoft.com/en-us/research/uploads/prod/2006/01/Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf

同じ問題設定においてデータを逐次的に投下した場合、まず事前分布に対してデータ空間を観測しパラメータの事後分布を得ることになる。ベイズ推論ではデータが増えた時に減少するパラメータの不確かさを見ることもできる。PRML p.155の図の通り、 w_0, w_1 の事後分布、尤度の平面が観測データの数によって変化し、事後分布が定まっていくのがわかる。

[1]より、逐次推論における事後分布と尤度の推移

また予測分布に関しても、PRML p.157 の通りデータ観測によって定まっていく。

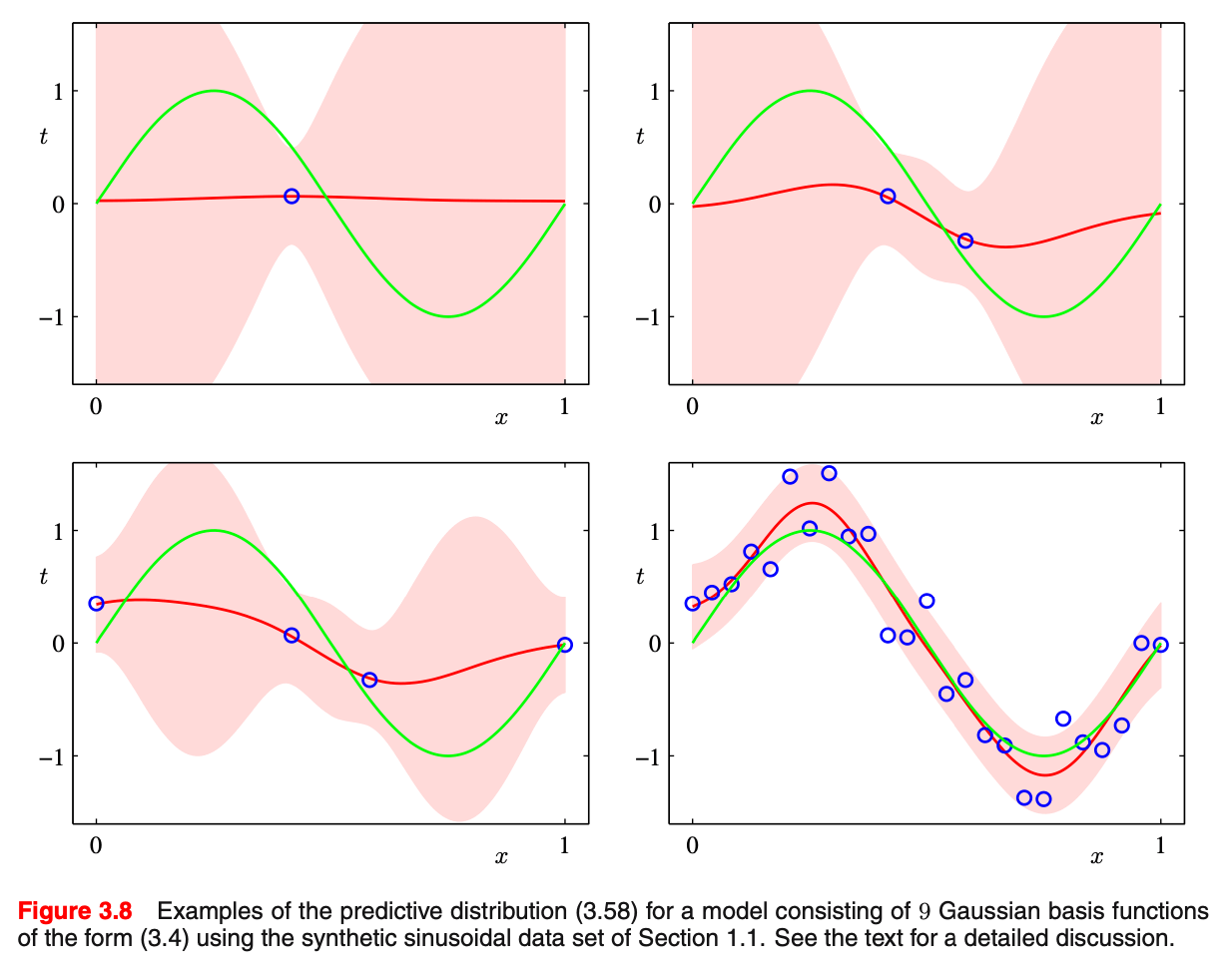[1]より、逐次推論における予測分布の推移

1. ロジスティック回帰

PRML 4.3.2

y(\bold{x}) = f(\bold{w}^\top \bold{x} + w_0)

活性化関数: fにより線形変換を非線形にする。
連結関数: 活性化関数の逆関数。すなわち、活性化関数は逆連結関数ともいえる。

単純な線形モデルでは活性化関数が恒等射として扱っているが、一般化線形モデル (generalized linear model; GLM)の枠組みになるともはやパラメータすら線形ではない。
この活性化関数としてシグモイド(logistic sigmoid)を用いることで、GLMで分類モデルを作ることができる。

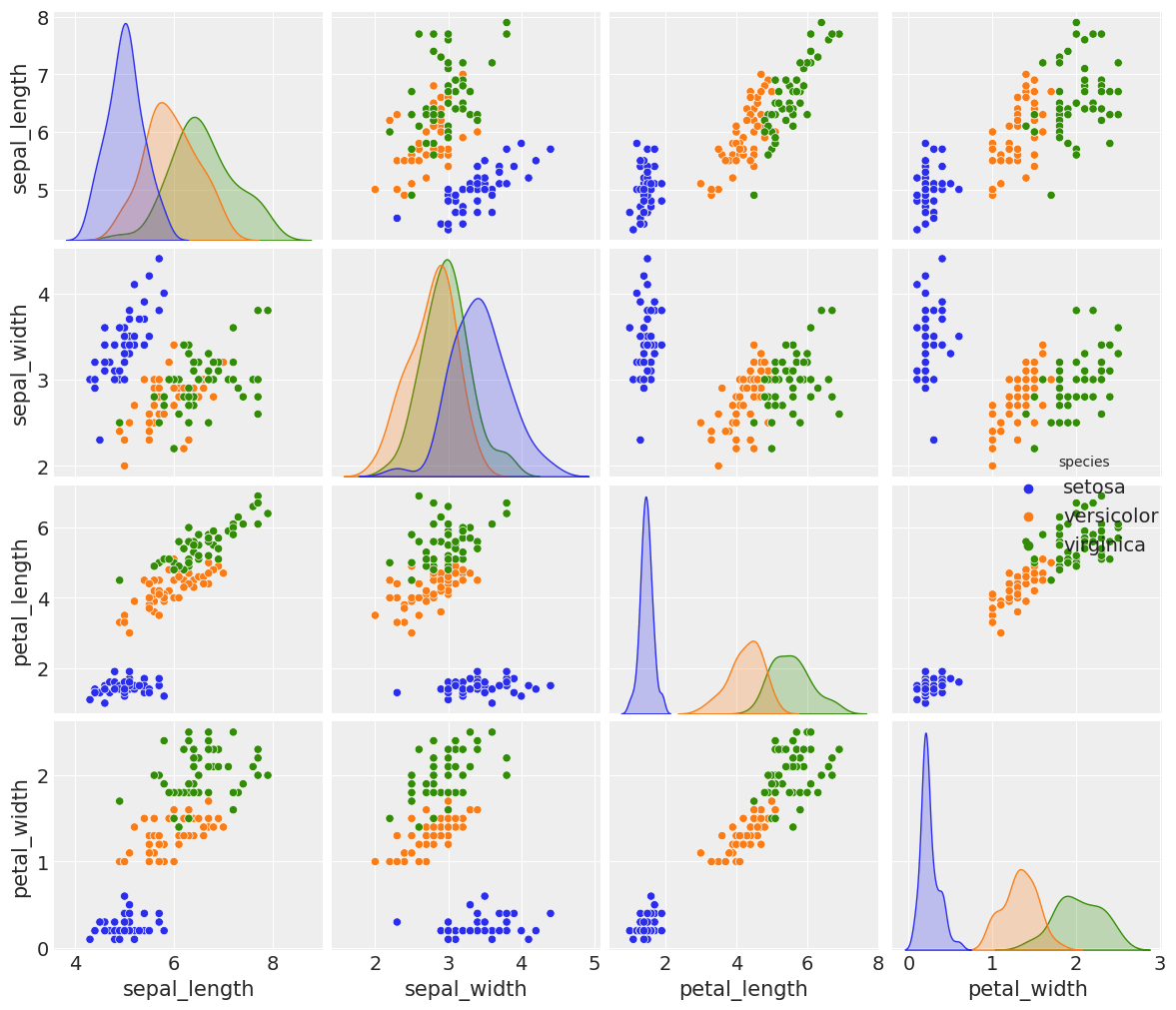
データセットとしてirisを使う。4つの独立変数と3つの種別があり、今回は簡単に1つの独立変数と2つの種別の分類について考える。

iris = sns.load_dataset("iris")
sns.pairplot(iris, diag_kind="kde", hue="species")


dataset = pd.concat([iris[iris["species"] == "versicolor"], iris[iris["species"] == "setosa"]])
y = pd.Categorical(dataset["species"]).codes
x = dataset["sepal_length"].values

with pm.Model() as model:
    w0 = pm.Normal("w0", mu=0, sigma=10)
    w1 = pm.Normal("w1", mu=0, sigma=10)
    mu = pm.Deterministic("mu", w0 + pm.math.dot(x, w1))
    theta = pm.Deterministic("theta", 1/(1 + pm.math.exp(-mu)))
    bd = pm.Deterministic("bd", -w0/w1)
    y_pred = pm.Bernoulli("y_pred", p=theta, observed=y)

    trace = pm.sample(1000, chains=2, cores=1)

az.plot_trace(trace, var_names=["w0", "w1", "bd"])
az.plot_autocorr(trace, var_names=["w0", "w1", "bd"], combined=True)
az.summary(trace, var_names=["w0", "w1", "bd"])
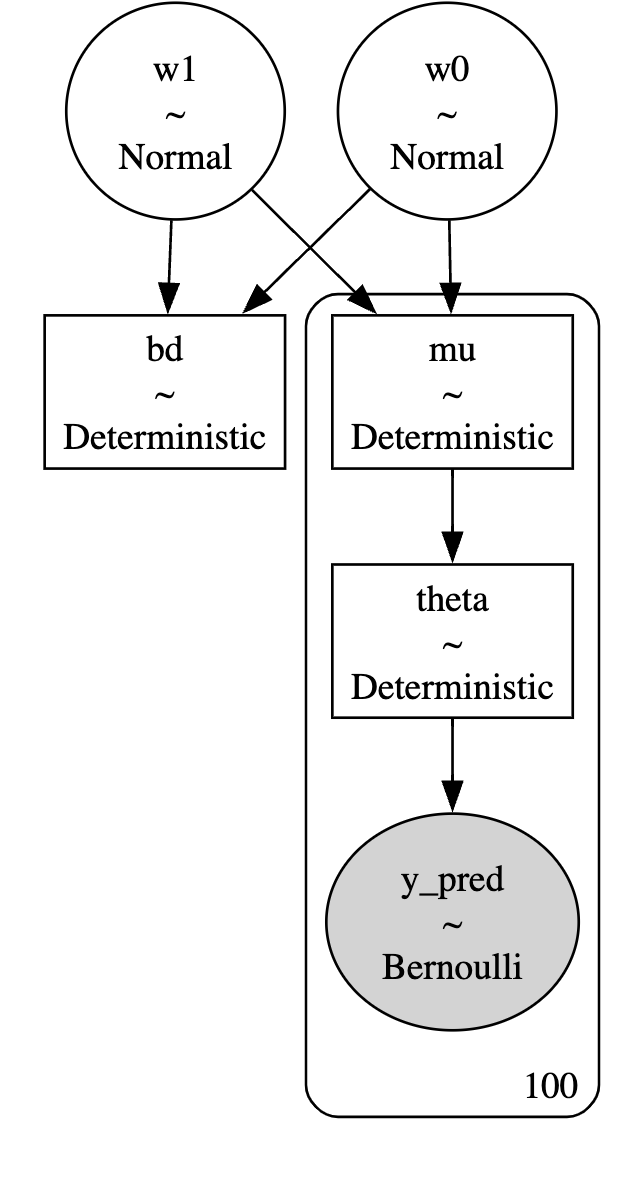
pm.model_to_graphviz(model=model)
output

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
w0	-23.360	3.763	-30.394	-16.738	0.217	0.154	294.0	355.0	1.0
w1	4.314	0.698	3.073	5.614	0.040	0.028	295.0	314.0	1.0
bd	5.416	0.069	5.283	5.548	0.002	0.001	1751.0	1296.0	1.0




print(trace.posterior)

idx = np.argsort(x)
post_theta = trace.posterior["theta"].values
post_theta_hdi = az.hdi(trace.posterior, hdi_prob=0.90)["theta"].values
post_bd = trace.posterior["bd"].values
post_bd_hdi = az.hdi(trace.posterior, hdi_prob=0.90)["bd"].values

plt.scatter(x, y, color="b")
plt.plot(x[idx], post_theta.mean(axis=(0,1))[idx], color="r")
plt.fill_between(x[idx], post_theta_hdi[idx][:,0], post_theta_hdi[idx][:,1], color="r", alpha=0.4)
plt.axvline(post_bd.mean(), ymax=1, color="r")
plt.fill_betweenx(y=[0,1], x1=post_bd_hdi[0], x2=post_bd_hdi[1], color="r", alpha=0.4)
output
<xarray.Dataset>
Dimensions:      (chain: 2, draw: 1000, mu_dim_0: 100, theta_dim_0: 100)
Coordinates:
  * chain        (chain) int64 0 1
  * draw         (draw) int64 0 1 2 3 4 5 6 7 ... 993 994 995 996 997 998 999
  * mu_dim_0     (mu_dim_0) int64 0 1 2 3 4 5 6 7 8 ... 92 93 94 95 96 97 98 99
  * theta_dim_0  (theta_dim_0) int64 0 1 2 3 4 5 6 7 ... 92 93 94 95 96 97 98 99
Data variables:
    w0           (chain, draw) float64 -21.82 -23.99 -23.83 ... -29.68 -29.26
    w1           (chain, draw) float64 4.047 4.409 4.373 ... 5.465 5.446 5.431
    mu           (chain, draw, mu_dim_0) float64 6.511 4.083 ... -0.477 -2.106
    theta        (chain, draw, theta_dim_0) float64 0.9985 0.9834 ... 0.1085
    bd           (chain, draw) float64 5.391 5.441 5.449 ... 5.45 5.45 5.388
Attributes:
    created_at:                 2024-01-06T19:34:46.653198
    arviz_version:              0.13.0
    inference_library:          pymc
    inference_library_version:  5.9.0
    sampling_time:              3.5929160118103027
    tuning_steps:               1000

モデルの定義より θ = σ(w_0 + w_1 x) であり、 σ(x) = \frac{1}{1 + e^{-x}} より次の決定境界のx座標が得られる。

\begin{aligned} 0.5 &= σ(w_0 + w_1 x) \\ 0 &= w_0 + w_1 x \\ x &= -\frac{w_0}{w_1} \end{aligned}

2. 重ロジスティック回帰

独立変数の数を増やす。決定境界の議論については1変数の時と簡単に拡張することができる。

\begin{aligned} 0.5 &= σ(w_0 + w_1 x_1 + w_2 x_2) \\ 0 &= w_0 + w_1 x_1 + w_2 x_2 \\ x_1 &= -\frac{w_0}{w_1} - \frac{w_2}{w_1} x_2 \end{aligned}

n変数の決定境界は超平面の方程式で表現でき、計算で求める事ができる。

dataset = pd.concat([iris[iris["species"] == "versicolor"], iris[iris["species"] == "setosa"]])
y = pd.Categorical(dataset["species"]).codes
x = dataset[["sepal_length", "sepal_width"]].values

with pm.Model() as model:
    w0 = pm.Normal("w0", mu=0, sigma=10)
    w = pm.Normal("w", mu=0, sigma=10, shape=2)
    mu = pm.Deterministic("mu", w0 + pm.math.dot(x, w))
    theta = pm.Deterministic("theta", 1/(1 + pm.math.exp(-mu)))
    bd = pm.Deterministic("bd", - w0/w[0] - w[1]/w[0] * x[:,1])
    y_pred = pm.Bernoulli("y_pred", p=theta, observed=y)

    trace = pm.sample(1000, chains=2, cores=1)

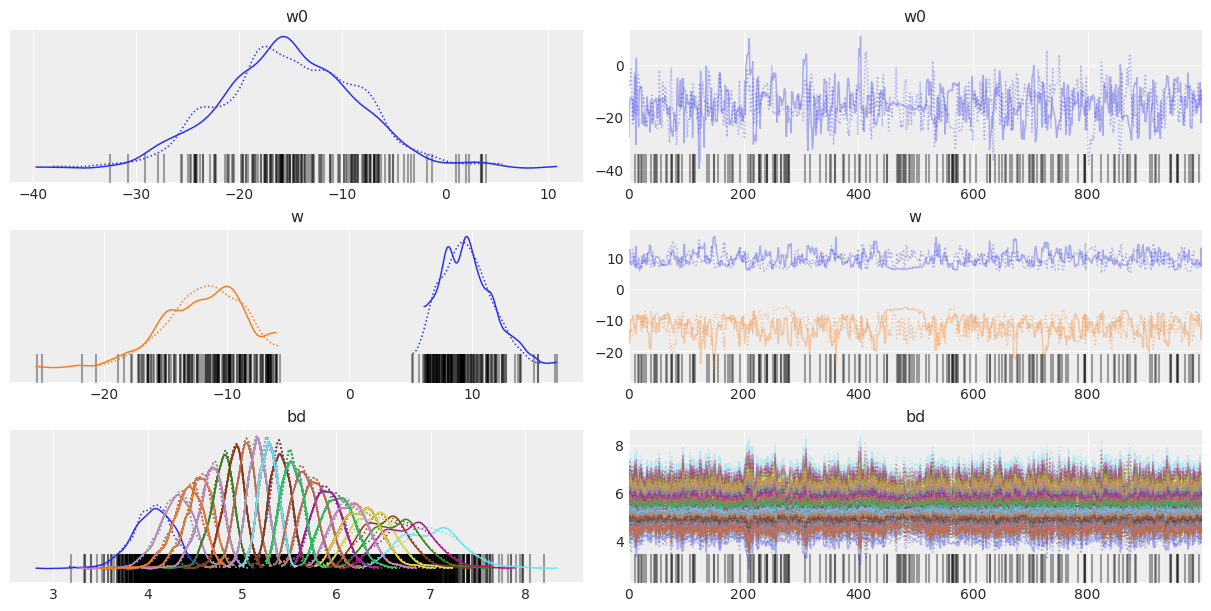
az.plot_trace(trace, var_names=["w0", "w", "bd"])
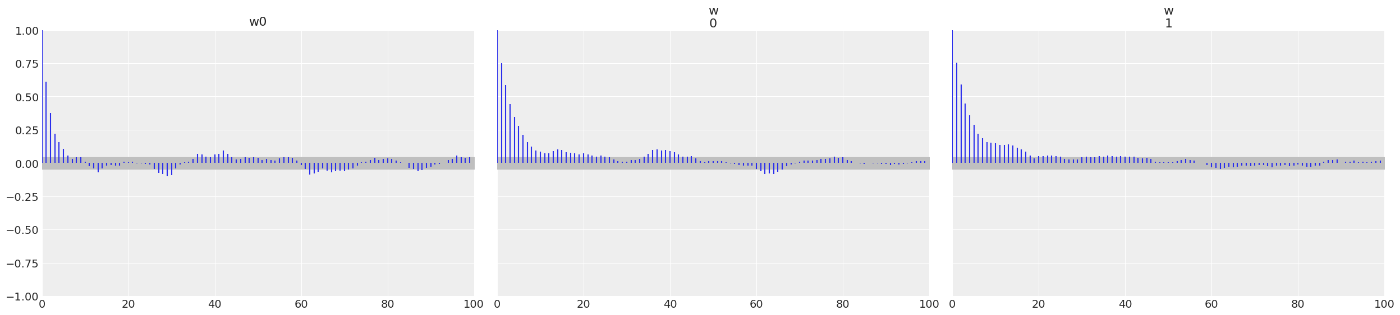
az.plot_autocorr(trace, var_names=["w0", "w"], combined=True)
az.summary(trace, var_names=["w0", "w"])
output
	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
w0	-15.157	6.737	-27.691	-2.919	0.311	0.220	471.0	551.0	1.00
w[0]	9.629	2.115	5.932	13.485	0.139	0.098	214.0	244.0	1.00
w[1]	-11.906	3.218	-17.557	-6.210	0.219	0.155	161.0	56.0	1.01



idx = np.argsort(x[:,1])

post_bd = trace.posterior["bd"].values
post_bd_hdi = az.hdi(trace.posterior, hdi_prob=0.90)["bd"].values

print(post_bd_hdi[:,0].shape)

plt.scatter(x[:,1], x[:,0], c=y, cmap="viridis")
plt.plot(x[:,1][idx], post_bd.mean(axis=(0,1))[idx], color="r")
plt.fill_between(x[:,1][idx], post_bd_hdi[:,0][idx], post_bd_hdi[:,1][idx], color="r", alpha=0.4)

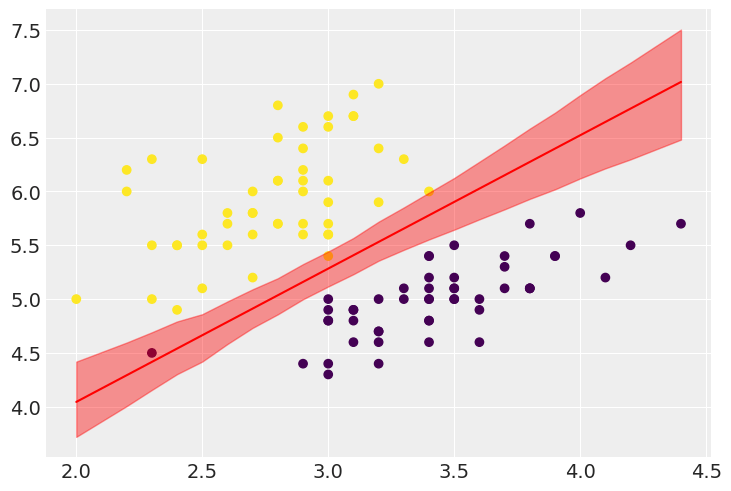
相関のある変数

相関が高い変数を入れる場合、変数にモデルへの成約を与えるパワーが少なくなる。これをなんとかするため、事前分布に強い情報を与えることである。Andrew GelmanとStanチームは \bold{w} の事前分布としてT分布を使うことを提案している。

\bold{w} \sim \mathcal{T}(0, ν, s)

ν は3~7くらい、 s はスケールの平均値の情報を与えるようにする。

# irisデータの共分散行列を可視化し、各変数の相関を見る

corr = iris[iris["species"] != "virginica"].corr()
mask = np.tri(*corr.shape).T
sns.heatmap(corr.abs(), mask=mask, annot=True, cmap="viridis")

ロジスティック回帰係数の解釈

シグモイド活性化関数は非線形なので、回帰係数を解釈する場合は注意する必要がある。
この逆関数であるロジット関数 \text{logit}(z) = \log(\frac{z}{1-z}) を使うと次のように表せる。

\begin{aligned} θ &= σ(w_0 + \bold{w x}) \\ \text{logit}(θ) &= w_0 + \bold{w x} \\ \log(\frac{θ}{1-θ}) &= w_0 + \bold{w x}) \end{aligned}

θ が y = 1 であることを思い出すと次のような式が導ける。

\log(\frac{p(t=1)}{1-p(t=1)}) = w_0 + \bold{w x}

対数オッズ: 特にこの真数部分はオッズ として知られ、係数 \bold{x} は変数 \bold{x} の単位量増加がオッズの対数の増加量にどれだけ対応しているかを表している。しかし、線形な関数ではないので変化量の大きさを比較するのは難しい。

ソフトマックス回帰

複数クラスの分類に拡張する。

\text{softmax}_k(\bold{x}, \bold{w}) = \frac{e^{\bold{w}_k^\top \bold{x}}}{\sum_{j} e^{\bold{w}_j^\top \bold{x}}}

irisデータセットを全て使って、複数独立変数から複数クラス分類を行う。

y = pd.Categorical(iris["species"]).codes
x = iris[["sepal_length", "sepal_width", "petal_length", "petal_width"]].values
x = (x - x.mean(axis=0))/x.std(axis=0)

with pm.Model() as model:
    w0 = pm.Normal("w0", mu=0, sigma=10, shape=3)
    w = pm.Normal("w", mu=0, sigma=10, shape=(4,3))
    mu = pm.Deterministic("mu", w0 + pm.math.dot(x, w))
    theta = pm.Deterministic("theta", pm.math.softmax(mu, axis=1))  # axis設定しないとダメになるので注意
    y_pred = pm.Categorical("y_pred", p=theta, observed=y)

    trace = pm.sample(1000, chains=2, cores=1)

az.plot_trace(trace, var_names=["w0", "w"])
az.summary(trace, var_names=["w0", "w"])
pm.model_to_graphviz(model=model)



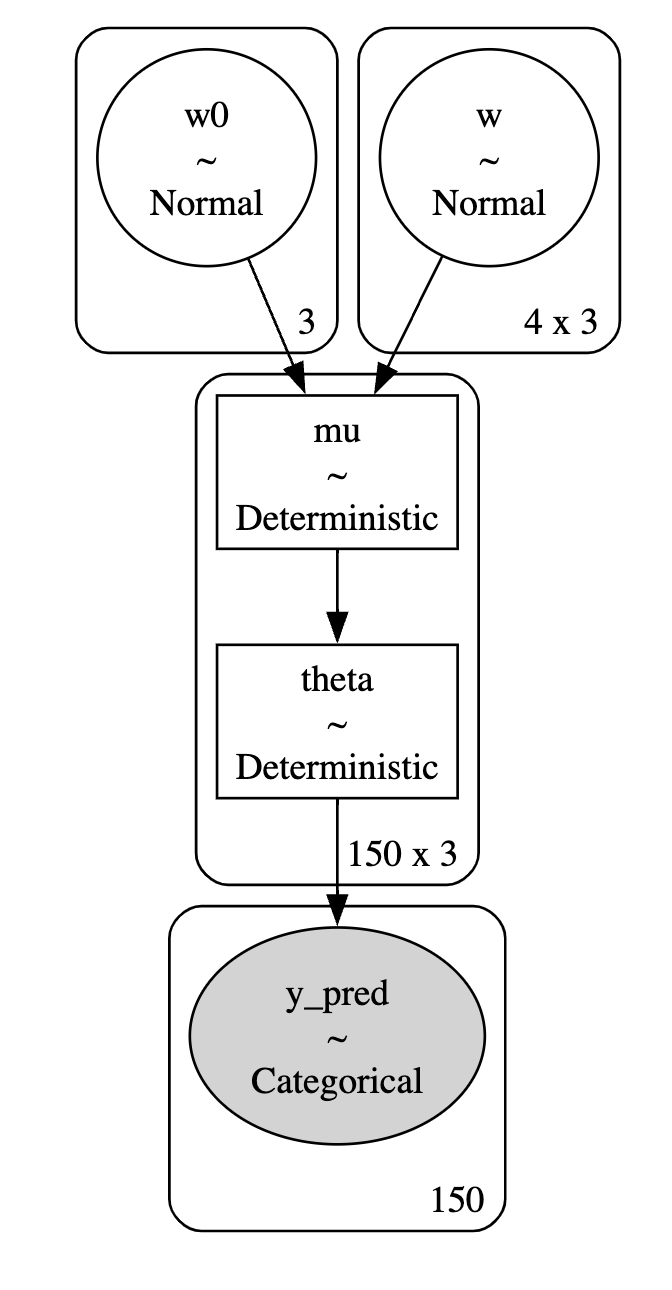
post_w0 = trace.posterior["w0"].values
post_w = trace.posterior["w"].values
pred_list = post_w0.mean(axis=(0,1)) + np.dot(x, post_w.mean(axis=(0,1)))
pred = []

for p in pred_list:
    pred.append(np.exp(p)/np.sum(np.exp(p), axis=0))
acc = np.sum(y == np.argmax(pred, axis=1))/len(y)
print(acc)
output
0.98

98%の精度で分類できている。

3. 識別モデルと生成モデル

PRML 4.2 4.3

識別モデル(discriminative model): 今までは当該クラス C_k と関連するとして測定された変数 x を観測した下で与えられたクラスの確率 p(C_k|x) を直接計算していた。言い換えると、独立変数から従属変数へ直接的に写像するモデルを作って、閾値で連続的な確率を離散クラスへ割り当てていた。

生成モデル(generative model): 最初にクラスの事前分布 p(C_k) と各クラスに関する x の分布 p(x|C_k) をモデリングして、その後クラスへ割り当てる。

p(C_k|x) = \frac{p(x|C_k)p(C_k)}{\sum_{j} p(x|C_j)p(C_j)}

線形判別分析(linear discriminant analysis; LDA)は正規分布の各 μ_k の中間を決定境界とする分類モデルで、紛らわしい名前だが生成モデルの1つである。
以下ではLDAによりirisが生成される p(C_k|x) をモデリングし、分類を行う。

y = pd.Categorical(iris["species"]).codes
x = iris[["sepal_length", "sepal_width", "petal_length", "petal_width"]].values
x = (x - x.mean(axis=0))/x.std(axis=0)

with pm.Model() as model:
    mu = pm.Normal("mu", mu=0, sigma=10, shape=(3, 4))
    sigma = pm.HalfCauchy("sigma", 5, shape=(3, 4))
    c00 = pm.Normal("c00", mu=mu[0,0], sigma=sigma[0,0], observed=x[0:50, 0])
    c01 = pm.Normal("c01", mu=mu[0,1], sigma=sigma[0,1], observed=x[0:50, 1])
    c02 = pm.Normal("c02", mu=mu[0,2], sigma=sigma[0,2], observed=x[0:50, 2])
    c03 = pm.Normal("c03", mu=mu[0,3], sigma=sigma[0,3], observed=x[0:50, 3])
    c10 = pm.Normal("c10", mu=mu[1,0], sigma=sigma[1,0], observed=x[50:100, 0])
    c11 = pm.Normal("c11", mu=mu[1,1], sigma=sigma[1,1], observed=x[50:100, 1])
    c12 = pm.Normal("c12", mu=mu[1,2], sigma=sigma[1,2], observed=x[50:100, 2])
    c13 = pm.Normal("c13", mu=mu[1,3], sigma=sigma[1,3], observed=x[50:100, 3])
    c20 = pm.Normal("c20", mu=mu[2,0], sigma=sigma[2,0], observed=x[100:150, 0])
    c21 = pm.Normal("c21", mu=mu[2,1], sigma=sigma[2,1], observed=x[100:150, 1])
    c22 = pm.Normal("c22", mu=mu[2,2], sigma=sigma[2,2], observed=x[100:150, 2])
    c23 = pm.Normal("c23", mu=mu[2,3], sigma=sigma[2,3], observed=x[100:150, 3])

    trace = pm.sample(1000, chains=2, cores=1)

az.plot_trace(trace, var_names=["mu", "sigma"])
az.summary(trace)
pm.model_to_graphviz(model=model)


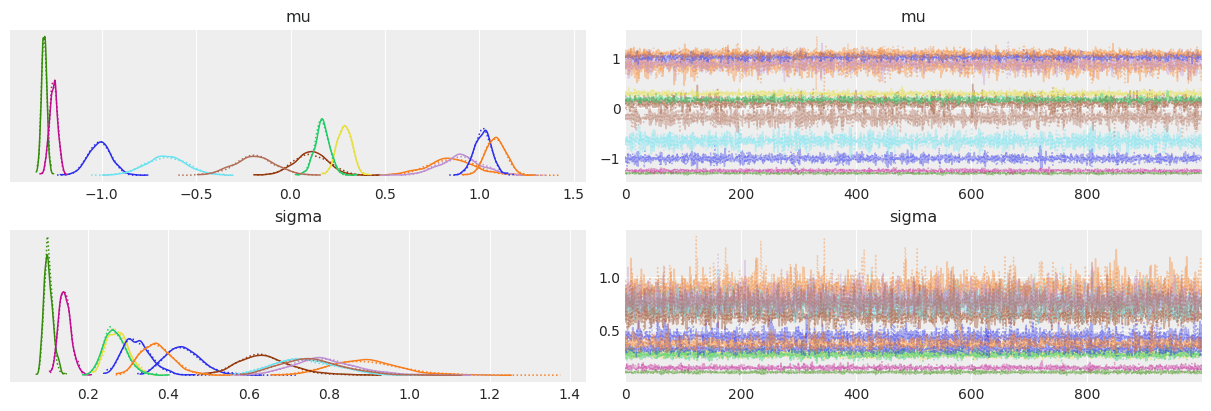
# データ生成が実データと合っているか確認
myposterior = pm.sample_posterior_predictive(trace, model=model)
az.plot_ppc(myposterior, num_pp_samples=20, kind="scatter")
plt.show()

# c00(C="setosa", x="sepal_length")とc10(C="versicolor", x="sepal_length")の境界を見てみる
post_mu00 = trace.posterior["mu"].values[:,:,0,0]  # shape [chain, sample, class, feat]
post_mu10 = trace.posterior["mu"].values[:,:,1,0]
post_mu00_hdi = az.hdi(trace.posterior, hdi_prob=0.90)["mu"].values[0,0]  # shape [class, feat, 2(=top+bottom)]
post_mu10_hdi = az.hdi(trace.posterior, hdi_prob=0.90)["mu"].values[1,0]
plt.scatter(x[0:100, 0], y[0:100], color="b")
plt.axvline((post_mu00.mean()+post_mu10.mean())/2, ymax=1, color="r")
plt.fill_betweenx(y=[0,1], x1=(post_mu00_hdi[0]+post_mu10_hdi[0])/2, x2=(post_mu00_hdi[1]+post_mu10_hdi[1])/2, color="r", alpha=0.4)
plt.show()


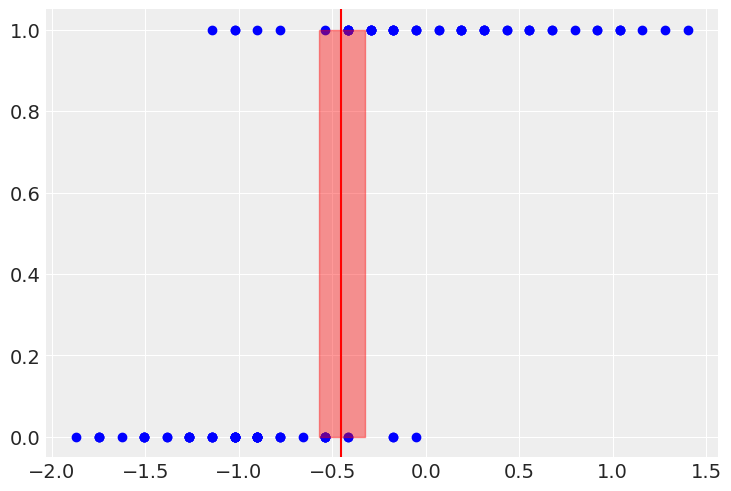
自作のモデルは共通の分散を仮定するLDAというよりは、2次線形識別器(quadratic linear discriminant analysis; QDA)になっている気がする。この場合は決定境界は線形ではなく2次曲線になる。

一般的には分析に使うデータが正規分布に従う場合はLDAやQDAが良いが、そもそもデータが正規分布に従ってない場合はロジスティック回帰のほうが良い予測を与える。識別モデルはモデルに組み込む母数の情報がある場合に、簡単に自然に事前分布にそれを与えられることである(?)。

LDAやQDAの決定境界は閉じていて、分布の期待値を求めるだけで決定境界を得られる。ベイズでは代数計算など難しい制約なしに、例えばツールとしてT分布を使って決定境界を求めるなど、閉形式の解を求められなくても計算ができてしまう良さがある。

感想

今回はPRMLのガウス分布を用いたときの代数計算による結果を振り返りながらPyMCによるサンプリング計算ベースのプログラムで実演するという形で勉強した。
今まで確認不足や不慣れもあって、勉強ノート1~4では微妙に間違った言葉などを書いていたので時間があったら直しておきたい...

ただ、線形回帰から振り返ってある程度手に馴染んできた感じはあるので、何らかのデータで実際に遊んでみようと思う。

https://jhalfmoon.com/dbc/2022/02/01/データのお砂場14-r言語、insectsprays、殺虫剤の効きの分散/

https://jhalfmoon.com/dbc/2022/03/16/データのお砂場21-r言語、orchardsprays、果樹園用農薬？の効/

https://jhalfmoon.com/dbc/2022/03/23/データのお砂場22-r言語、plantgrowth、植物の成長実験/

Discussion