Bayesian Analysis with PyMC 勉強ノート 6 モデル比較

Osvaldo Martin 著, 金子武久 訳
Pythonによるベイズ統計モデリング (Bayesian Analysis with Python)
2018-06-26
https://www.kyoritsu-pub.co.jp/book/b10003944.html

Christopher M. Bishop 著, 元田浩 栗田多喜夫 樋口知之 松本裕治 村田昇 監訳
パターン認識と機械学習 ベイズ理論による統計的予測 (Pattern Recognition and Machine Learning)
2012-01-20
https://www.maruzen-publishing.co.jp/item/?book_no=294524

Pythonによるベイズ統計モデリングを読んだので学習メモを整理します。学習中のノートなので正確ではないかもしれません。使われているコードをPyMC3からPyMC5に書き直しました。
また、せっかくなのでPRMLの本を参照しながら読むことにしました。式の文字の扱いなどはPRML風になるよう頭に収めようと思っています。

https://www.kyoritsu-pub.co.jp/book/b10003944.html

https://www.pymc.io/welcome.html

モデル比較

モデルはデータを通じて問題を理解するためのただの近似であるため、あらゆるモデルは間違っていると言える。しかしその中でも同じデータを記述する他のモデルと比較した時に優劣がある。

• 単純さと精度
• 過学習と過小適合
• 正則化事前分布
• 情報量基準
• ベイズファクター

次のライブラリを使用する。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

import pymc as pm
import arviz as az

az.style.use("arviz-darkgrid")

0. ベイズモデルについての復習

モデル比較のための前提知識を思い出すために、PRMLの本を読みながらメモしていく。

多項式曲線fitting

PRML 1.1

モデル設定を司る変数 $M$ を持つ線形モデルとして多項式曲線 $y_M(x, \bold{w})$ を考える。

$$\begin{aligned} y_M(x, \bold{w}) &= w_0 + w_1 x^1 + w_2 x^2 + w_3 x^3 + \dots w_M x^M \\ &= \sum_{m=0}^{M} w_m x^m \end{aligned}$$

• $\bold{x} = \{ x_n \}$: 入力データ
• $\bold{t} = \{ t_n \}$: $x$ に対応する目標データ

$t$ はデータ生成元のモデルにガウスノイズを加えた値になっている。このノイズは確率的、統計的(stochastic)にランダムなプロセスのものもあるが、大体はそれ自身は観測されない信号源の変動によるもので、 $x$ に対する $t$ には不確実性 (uncertainty)がある。
このデータに対して、新たな入力 $\hat{x}$ を与えたときの目標値 $\hat{t}$ を予測する。

単純な方法では、誤差関数 (error function) $E(\bold{w}) = \frac{1}{2} \sum_{n=1}^{N} (y_M(x, \bold{w}) - t_n)^2$ を最小にするパラメータ $\bold{w}^\ast$ を求める。このモデルでは $E$ が $\bold{w}$ の2次関数なので、パラメータに関する勾配が1次になってくれるので唯一の閉じた解が定まる。

$M$ が小さすぎるとデータ点を殆ど表現できず学習誤差と汎化誤差が共に大きなままだが、逆に $M$ が大きすぎると学習誤差は0に近づくものの発散がひどくなり汎化誤差が大きくなる。
以上の話で出てきた最小二乗でパラメータを最適化した場合の過学習の性質は、アプローチが最尤推定 (maximum likelihood)の特殊な場合に相当するから起こっている。最尤推定の一般的性質である。

このアプローチのまま過学習を抑えるには正則化 (regularization)を加える方法があり、これにより汎化誤差を緩和できる。(が、聞くところによると、データに対する不偏性(unbiasedness; サンプルサイズに依存せず推定量の期待値が母数に等しい性質)や一致性(consistency; 無限大のサンプルサイズで計算した推定値が母数に一致する性質)などの観点から、説明性の点であまり良くないこともあるらしい)

$$E(\bold{w}) = \frac{1}{2} \sum_{n=1}^{N} (y_M(x, \bold{w}) - t_n)^2 + \frac{λ}{2}||\bold{w}||^p$$

$λ$ の値は正則化の強さを制御する。特に $p=2$ の場合はRidge推定、 $p=1$の場合はLasso推定と言い、縮小推定 (shrinkage)の有名な方法である。特にNN界隈では重み減衰(weight decay)として知られる。

ベイズ確率における曲線fitting

PRML 1.2

最尤推定などのような頻度主義(frequentist)的なアプローチではなく、ベイズ確率の方法で推定することで、自然に過学習を押さえながら不確実性を定量化し、さらに有効パラメータ数 (effective number of parameters)を自動的にデータセットのサイズに適合させられる。

まず、パラメータ $\bold{w}$ に対する知識をもとに事前分布(prior) $p(\bold{w})$ を作る。なにも知らな場合は無情報なガウスなどで良い。データ $\mathcal{D}$ の観測による効果は条件付き確率(尤度関数) $p(\mathcal{D}|\bold{w})$ として陽に表せる。(尤度は確率分布ではないので積分が1になるとは限らない点に注意)

$$\begin{aligned} p(\bold{w}|\mathcal{D}) &= \frac{p(\mathcal{D}|\bold{w}) p(\bold{w})}{p(\mathcal{D})} \\ &= \frac{p(\mathcal{D}|\bold{w}) p(\bold{w})}{\int p(\mathcal{D}|\bold{w}) p(\bold{w}) d\bold{w}} \end{aligned}$$

ベイズの定理から、データ $\mathcal{D}$ の観測により情報を得て、 $\bold{w}$ の不確実性を評価した事後分布 $p(\bold{w}|\mathcal{D})$ が得られるというアイディアで、 $\bold{w}$ を推定できる。 $p(\mathcal{D})$ は右辺の積分が1になることを保証する規格化定数であるとも考えれる。

頻度主義では $\bold{w}$ を単にパラメータの値として推定量として、推定の可能な誤差範囲を $\mathcal{D}$ の分布を考慮して求めるが、ベイズでは唯一の観測されたデータ $\mathcal{D}$ があって、パラメータの不確実性が $\bold{w}$ の確率分布として求められる。
最尤推定では、 $\bold{w}$ は尤度 $p(\mathcal{D}|\bold{w})$ を最大にする値である。これは観測されたデータ集合の確率を最大化する $\bold{w}$ を選ぶことに相当する。誤差関数は尤度の対数を負にした単調減少関数であり、つまり尤度最大化は誤差関数最小化と等価である。

ベイズ的方法は全パラメータ空間で周辺化(つまり総和や積分)を計算する必要があるので、計算的な困難さから昔はあまり発展しなかった。しかしMCMCの実用化で様々なモデルを計算できるようになった。MCMCは計算量が大きい欠点があるが、変分ベイズや期待値伝播法などの計算量の小さい決定論的近似法もあり、大規模なモデルの計算も可能になる。

曲線fittingをベイズ的に考える。
まず、目標変数の値に関する不確実性を分布で表す。推定したいパラメータとして精度(分散の逆)を $β$ とする。

$$p(t | x,\bold{w},β) = \mathcal{N}(t | y_M(x,\bold{w}), β^{-1})$$

次に尤度(と対数尤度)を考える。データがiidからサンプルされた設定とする。

$$\begin{aligned} p(\bold{t} | \bold{x},\bold{w},β) &= \prod_{n=1}^{N} \mathcal{N}(t_n | y_M(x_n,\bold{w}), β^{-1}) \\ \ln p(\bold{t} | \bold{x},\bold{w},β) &= -\frac{β}{2} \sum_{n=1}^{N} (y_M(x_n, \bold{w}) - t_n)^2 + \frac{N}{2} \ln β - \frac{N}{2} \ln 2π \end{aligned}$$

この最尤推定を行えばパラメータ $\bold{w}^\ast, β^\ast$ が頻度論的に求まり、その推定量から予測分布 (predictive distribution) $p(\bold{t} | \bold{x},\bold{w}^\ast,β^\ast)$ が得られるが、ベイズではさらに事前分布 $p(\bold{w})$ を導入する。ハイパラメータとして事前分布の精度(分散の逆)を $α$ とする。

$$\begin{aligned} p(\bold{w}|α) &= \mathcal{N}(\bold{w} | \bold{0}, α^{-1}\bold{I}) \\ &= (\frac{α}{2π})^{\frac{M+1}{2}} e^{-\frac{α}{2}\bold{w}^\top \bold{w}} \end{aligned}$$

事前分布と尤度の積があれば、事後分布が求まる。これを最大化することを最大事後確率推定(maximum posterior; MAP推定)と言い、事後分布の最大値は以下の式で表せる事になる。

$$\frac{β}{2} \sum_{n=1}^{N} (y_M(x_n, \bold{w}) - t_n)^2 + \frac{α}{2}\bold{w}^\top \bold{w}$$

この美しい流れから、ガウスを使ったMAP推定は $λ=α/β$ のRidge回帰と等価で、単純な最尤推定よりロバストにモデルを最適化できることが示された。
さらにベイズ的な方法に従うと、事後分布 $p(\bold{w} | \bold{x}, \bold{t})$ を使って確率の乗法定理から予測分布を次の形で得られる。事前分布がガウスなら簡単な計算で求まる。

$$p(t | x, \bold{x}, \bold{t}, α, β) = \int p(t|x,\bold{w}) p(\bold{w} | \bold{x}, \bold{t}) d\bold{w}$$

1. 単純さと精度

オッカムのカミソリ (Occam's razor): 同じ現象を等しく説明する方法が複数ある場合、最も単純なものを選ぶこと。

精度が高く、かつ単純なモデルを選ぶことのバランスを考えていく。

# 多項式fittingのためのデータ生成

x = np.array([4.0, 5.0, 6.0, 9.0, 12.0, 14.0])
y = np.array([4.2, 6.0, 6.0, 9.0, 10.0, 10.0])
order = [0,1,2,5]  # モデルの複雑さ M
plt.scatter(x,y, color="b")

for m in order:
    x_n = np.linspace(x.min(), x.max(), 100)
    coeffs = np.polyfit(x, y, deg=m)
    ffit = np.polyval(coeffs, x_n)
    p = np.poly1d(coeffs)
    r2 = np.sum((p(x) - np.mean(y))**2) / np.sum((y - np.mean(y))**2)
    plt.plot(x_n, ffit, label=f"M = {m}, R^2 = {r2:.2f}")
plt.legend(loc=2, fontsize=14)

この図を見ると、必ずしも学習誤差(サンプル内精度 (within-sample accuracy)の逆)が小さいほうが良いというわけではなく、ある程度間違っていても単純な曲線のほうが物事をうまく説明できてそうな感じがしてくる。汎化誤差(サンプル外精度 (out-of-sample accuracy)の逆)が高い方が嬉しい。

バイアス-バリアンス分解

PRML 1.5.5 3.2

偏り(バイアス)と分散(バリアンス)のトレードオフを議論することで過学習と過小適合を説明できる。

• high bias: データに適合しにくく、データに含まれるパターンを見逃しやすい。偏見(prejudice)や慣性(inertia)が大きいモデルはバイアスが高く、表現力が小さい。
• high variance: 新しいデータセットを持ってきてモデルを最適化した時に、モデルが敏感に適合して形を大きく変える。データセットの種類により多くの変種を作れるモデルはhigh varianceを持つ。複雑で柔軟なモデルはバリアンスが高く、ノイズを過学習しやすい。

この2つはトレードオフになっていて、次の式から定量的に理解することができる。

条件付き分布 $p(t|\bold{x})$ が与えられればそれぞれの損失関数(例えば2乗誤差 $L(t, y(\bold{x})) = (y(\bold{x}) - t)^2$ を)に対して最適な予測(条件付き期待値)を与えられる。まず期待損失 $\mathbb{E}[E]$ は

$$\begin{aligned} \mathbb{E}[L] &= \iint L(t,y(\bold{x})) p(\bold{x}, t) d\bold{x}dt \\ &= \iint (y(\bold{x}) - t)^2 p(\bold{x}, t) d\bold{x}dt \end{aligned}$$

目標は $\mathbb{E}[E]$ を最小にする $y(\bold{x})$ を選ぶことで、変分法などを使い最小化を計算できて、結果は以下の式に表される。

$$\begin{aligned} \frac{∂\mathbb{E}[L]}{∂y(\bold{x})} &= 2 \int (y(\bold{x}) - t) p(\bold{x}, t) dt = 0 \\ \Leftrightarrow y(\bold{x}) &= \frac{\int t p(\bold{x}, t) dt}{p(\bold{x})} \\ &= \int t p(t|\bold{x}) dt \\ &= \mathbb{E}_t[t|\bold{x}] \end{aligned}$$

この結果を使って、 $(y(\bold{x}) - t)^2$ に $±\mathbb{E}_t[t|\bold{x}]$ を加えて展開することで、次のような表現もできる。

$$\begin{aligned} \mathbb{E}[L] &= \int (y(\bold{x}) - \mathbb{E}_t[t|\bold{x}])^2 p(\bold{x}) d\bold{x} + \int \mathbb{V}[t | \bold{x}] p(\bold{x}) d\bold{x} \\ &= \int (y(\bold{x}) - \mathbb{E}_t[t|\bold{x}])^2 p(\bold{x}) d\bold{x} + \int \int (\mathbb{E}_t[t|\bold{x}] - t)^2 p(t|\bold{x}) dt p(\bold{x}) d\bold{x} \\ &= \int (y(\bold{x}) - \mathbb{E}_t[t|\bold{x}])^2 p(\bold{x}) d\bold{x} + \iint (\mathbb{E}_t[t|\bold{x}] - t)^2 p(\bold{x}, t) d\bold{x} dt \end{aligned}$$

つまり $y(\bold{x})$ が $\mathbb{E}_t[t|\bold{x}]$ と等しい時最小になり、第1項目は0になる。
第2項目は $y(\bold{x})$ と独立で、データに含まれる本質的なノイズにのみ依存していて、達成可能な最小の期待損失を表している。

第1項目の中身を $(y(\bold{x}; \mathcal{D}) - \mathbb{E}_t[t|\bold{x}])^2)$ と表すと、この値はデータセット $\mathcal{D}$ に依存するので、データセットの取り方に関する期待値 $\mathbb{E}_{\mathcal{D}}[(y(\bold{x}; \mathcal{D}) - \mathbb{E}_t[t|\bold{x}])^2)]$ をバイアスとバリアンスに分解できて、それは以下になる。

$$\begin{aligned} \mathbb{E}_{\mathcal{D}}[(y(\bold{x}; \mathcal{D}) - \mathbb{E}_t[t|\bold{x}])^2)] \quad = \quad & ( \mathbb{E}_{\mathcal{D}}[(y(\bold{x}; \mathcal{D})] - \mathbb{E}_t[t|\bold{x}] )^2 \\ & + \quad \mathbb{E}_{\mathcal{D}}[ ( y(\bold{x}; \mathcal{D}) - \mathbb{E}_{\mathcal{D}}[y(\bold{x}; \mathcal{D})] )^2 ] \end{aligned}$$

第1項はバイアスで、全てのデータセットの取り方に関する出力の平均が、最適解(理想的な回帰関数) $\mathbb{E}_t[t|\bold{x}]$ とどのくらい乖離しているかを示している。
第2項はバリアンスで、 $y(\bold{x}; \mathcal{D})$ がデータセットに対してどのくらい敏感かを示している。
バイアスとバリアンスはトレードオフの関係になっていて、モデルの表現力、つまり複雑さでバランスする。例えば同じ複雑さ $M$ の多項式fittingにおいて、正則化項 $λ$ が小さすぎるモデルはバイアスが低いが過学習によりバリアンスが高いので汎化誤差が大きくなり悪いモデルになる。逆に $λ$ が大きすぎるモデルはバリアンスは低いが表現力が低くバイアスが高くなるので、同様に汎化誤差が大きくなり悪いモデルになる。

以上の議論で、誤差(期待損失 $\mathbb{E}[E]$ )がバイアス、バリアンス、データ含有ノイズの3つに分解できて、モデルの複雑さパラメータを調節してバイアス-バリアンスのパレート最適を見つける必要があることがわかった。

2. 事前分布の正則化

非ベイズにおいてはRidgeやLaasoなどが正則化として有名だが、これをベイズ的な視点で見ると、それぞれ $\bold{w}$ の事前分布にガウスを使っているかラプラス分布を使っているかの違いになっている

N = 20
a0_real = -0.3
a1_real = 0.5
e_real = np.random.normal(0, 0.2, N)
e_real[0] += 1
e_real[1] += 2
e_real[2] += 3

x = np.random.uniform(-1.0, 1.0, N)
y_real = a0_real + a1_real * x
y = y_real + e_real

plt.plot(x, y_real)
plt.scatter(x, y)

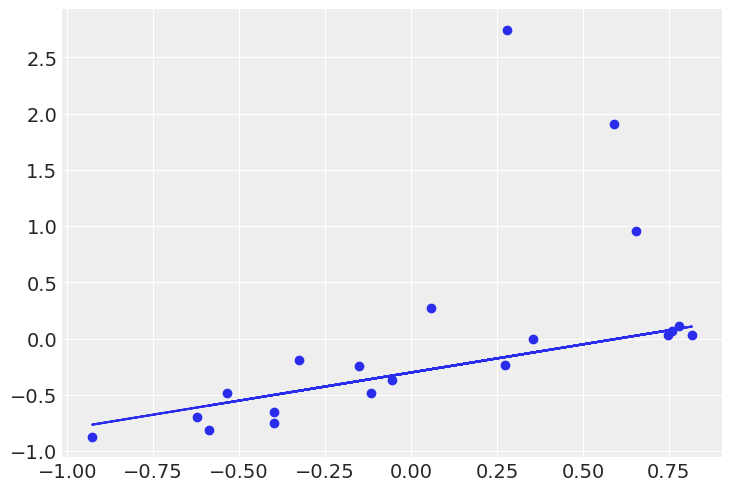
with pm.Model() as model_r:
    w0 = pm.Normal("w0", mu=0, sigma=10)
    w1 = pm.Normal("w1", mu=0, sigma=10)
    e = pm.HalfCauchy("epsilon", 5)
    mu = pm.Deterministic("mu", w0 + w1 * x)
    y_pred = pm.Normal("y_pred", mu=mu, sigma=e, observed=y)
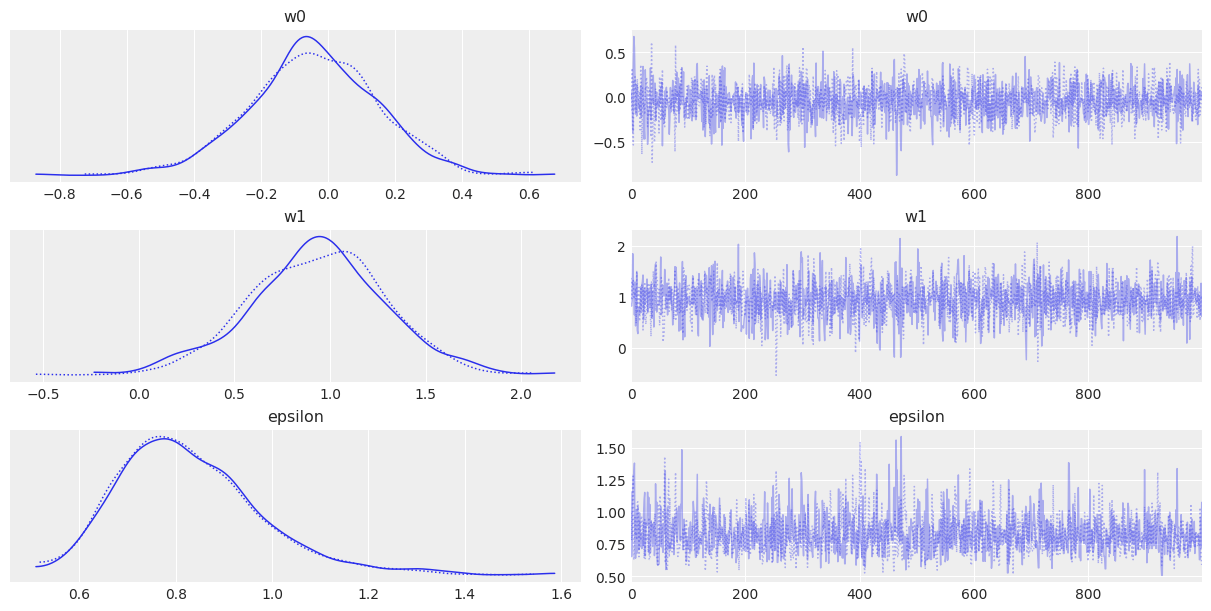
    trace_r = pm.sample(1000, chains=2, cores=1)
az.plot_trace(trace_r, var_names=["w0", "w1", "epsilon"])

with pm.Model() as model_l:
    w0 = pm.Laplace("w0", mu=0, b=10)
    w1 = pm.Laplace("w1", mu=0, b=10)
    e = pm.HalfCauchy("epsilon", 5)
    mu = pm.Deterministic("mu", w0 + w1 * x)
    y_pred = pm.Laplace("y_pred", mu=mu, b=e, observed=y)
    trace_l = pm.sample(1000, chains=2, cores=1)
az.plot_trace(trace_l, var_names=["w0", "w1", "epsilon"])

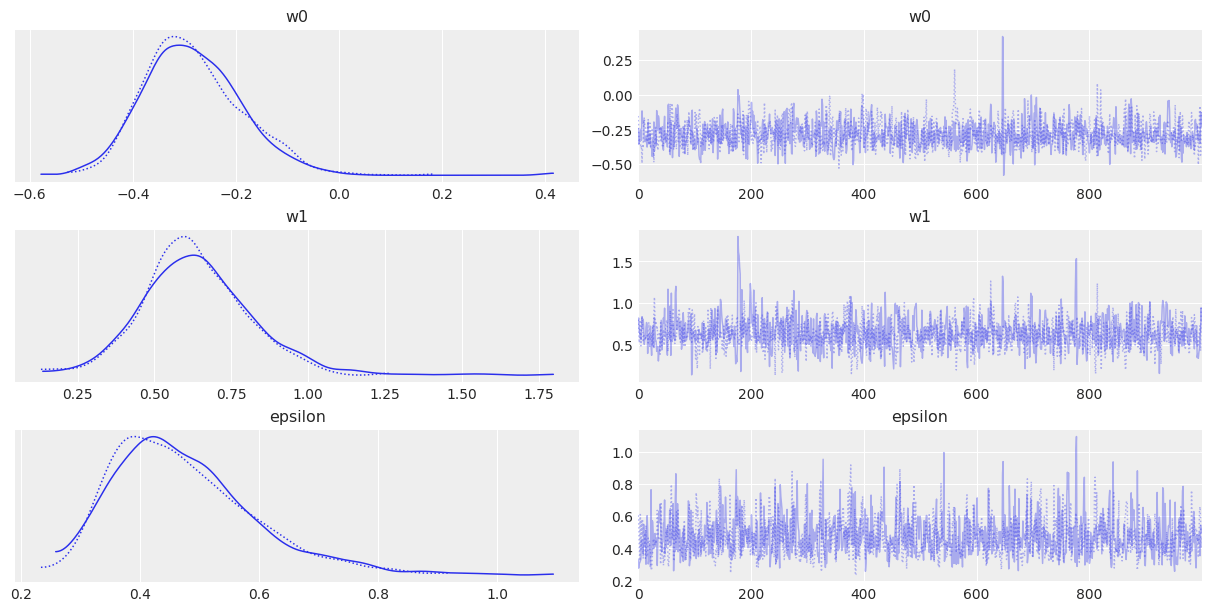
# パラメータの事後分布の可視化

fig, axes = plt.subplots(1, 2, figsize=(10,3))
axes = axes.ravel()
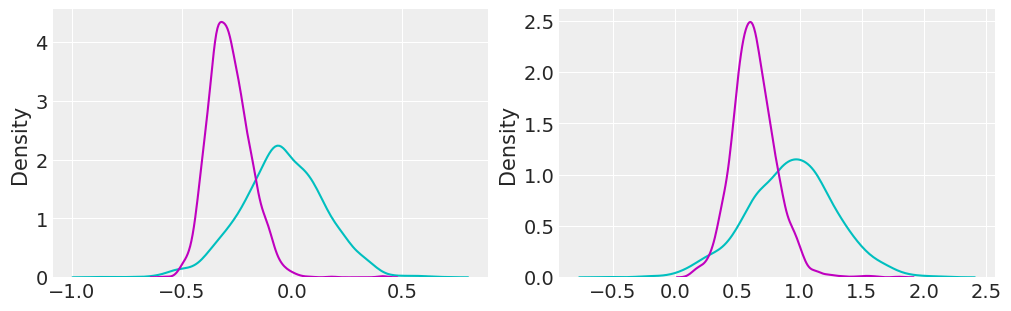
sns.kdeplot(trace_r.posterior["w0"].values.reshape(-1), color="c", ax=axes[0])
sns.kdeplot(trace_l.posterior["w0"].values.reshape(-1), color="m", ax=axes[0])
sns.kdeplot(trace_r.posterior["w1"].values.reshape(-1), color="c", ax=axes[1])
sns.kdeplot(trace_l.posterior["w1"].values.reshape(-1), color="m", ax=axes[1])
plt.show()

# データ空間上の予測分布

idx = np.argsort(x)
post_r_w0 = trace_r.posterior["w0"].values.reshape(-1)
post_r_w1 = trace_r.posterior["w1"].values.reshape(-1)
post_l_w0 = trace_l.posterior["w0"].values.reshape(-1)
post_l_w1 = trace_l.posterior["w1"].values.reshape(-1)

sig_r = az.hdi(trace_r.posterior, hdi_prob=0.90)["mu"].values[idx] 
sig_l = az.hdi(trace_l.posterior, hdi_prob=0.90)["mu"].values[idx]

plt.scatter(x, y)
plt.plot(x, np.mean(post_r_w0[idx])+np.mean(post_r_w1[idx])*x, c="c")
plt.plot(x, np.mean(post_l_w0[idx])+np.mean(post_l_w1[idx])*x, c="m")
plt.plot(x, a0_real + a1_real * x, c="b")
plt.fill_between(x[idx], y1=sig_r[:,0], y2=sig_r[:,1], color="c", alpha=0.20)
plt.fill_between(x[idx], y1=sig_l[:,0], y2=sig_l[:,1], color="m", alpha=0.20)
plt.show()

見た感じロバストに推定できている。ただT分布とどっちが良いかはわからない...

3. 予測精度

クロスバリデーションなどのためにデータを分割できない、したくない場合、情報量基準 (information criterion)を使ってモデルの精度をチェックできる。モデルの複雑さと精度(どれだけデータを説明できるか)のバランスを検討するための材料にできる。

対数尤度と逸脱度: 対数尤度 $\ln p(t|θ)$ は前述の通り精度の指標にできる。これをいい感じにした逸脱度 (deviance) $-2 \ln p(t|θ)$ は実用上よく使われる。

• 逸脱度が小さい、つまり対数尤度が大きいならデータのfit具合が良い
• 逸脱度は学習誤差(サンプル内精度)を測っているので、複雑なモデルを贔屓している
• 逸脱度に正則化項を入れることで贔屓を解消し、情報量基準として扱える

AIC 赤池情報量基準

$$\text{AIC} = -2 \ln p(t|\hat{θ}_{\text{mle}}) + 2k$$

$k$ はモデルに含まれるパラメータ数で、パラメータ数の数え方には複数の流儀がある。
$\hat{θ}_{\text{mle}}$ はパラメータに関する最尤推定量。(最尤推定は一様な事前分布に対するMAP推定量に等しい)

つまり、尤度でモデルの精度を見て、パラメータ数でモデルの複雑さを見ている情報量である。しかしベイズ的な観点では、事前分布に一様分布しか仮定していないのは扱いづらく、さらに事後分布の不確かさに関する情報も捨てられている( $\hat{θ}_{\text{mle}}$ は点推定量なので分布を反映できない)という点で良くない。良い事前分布は有効パラメータ数を単純計算上のパラメータ数より減らしてくれることを反映できる情報量がほしいと感じることになる。

DIC 逸脱度情報量基準

$$\text{DIC} = -2 \ln p(t|\hat{θ}_{\text{post}}) + 2k_\text{effective}$$

$k_\text{effective} = \mathbb{E}[-2 \ln p(t|θ)] - (-2 \ln p(t|\mathbb{E}[θ])$ はモデルの有効パラメータ数で、θの事後分布が狭いとこの正則化項も小さくなる。
$\hat{θ}_{\text{post}}$ はθの事後分布の平均値。

これは事後分布を反映したAICのベイズ版だが、まだ事後分布を全て使えていない。

WAIC 広く使える情報量規準

WAIC(Widely Available Information Criterion)

$$\text{WAIC} = -2 \sum_{i=1}^{N} \ln (\frac{1}{S} \sum_{s=1}{S} p(t_i|θ_s)) + 2 \sum_{i=1}^{N} \mathbb{V}_{s=1}^{S}[\ln p(t_i|θ_s)]$$

第1項目は対数各点予測密度(log point-wize predictive density)のサンプリングによる近似で、全データ点にわたり事後分布からサンプル $s$ に沿って尤度を計算し、それを合計する。
第2項目は有効パラメータ数の計算で、全データ点にわたり事後分布からサンプル $s$ に沿って対数尤度の分散を計算し、それを合計する。柔軟なモデルは広い事後分布を与える傾向がある。

# 1次式、2次式で回帰して

N = 30
a1_real, a2_real = 1.2, -1

x = np.random.uniform(-1.0, 1.0, N)
y = a1_real * x + a2_real * x**2 + np.random.normal(0, 0.5, N)
x = (x - x.mean())/x.std()
y = (y - y.mean())/y.std()

print(x.shape, y.shape)
plt.scatter(x, y, color="b")

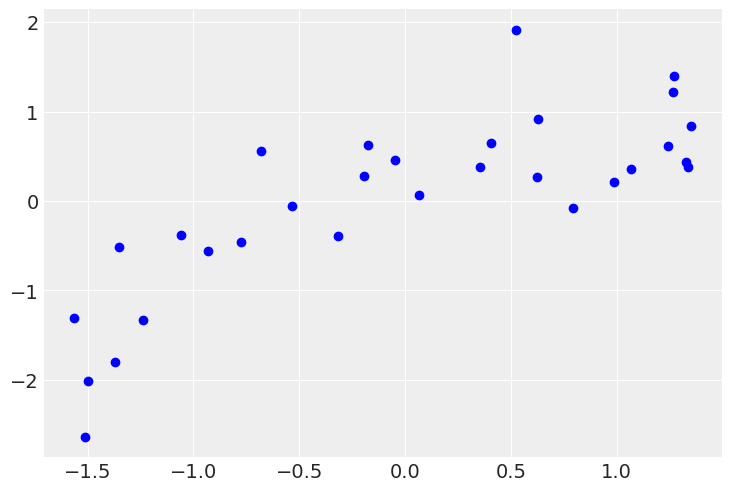
with pm.Model() as model_1:
    w0 = pm.Normal("w0", mu=0, sigma=10)
    w1 = pm.Normal("w1", mu=0, sigma=10)
    e = pm.HalfCauchy("epsilon", 5)
    mu = pm.Deterministic("mu", w0 + w1 * x)
    y_pred = pm.Normal("y_pred", mu=mu, sigma=e, observed=y)
    trace_1 = pm.sample(1000, chains=2, cores=1)
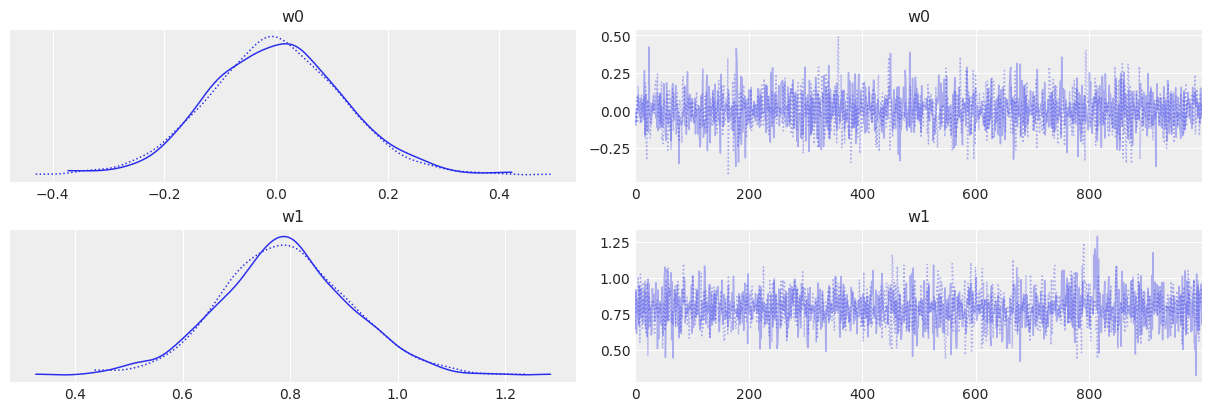
az.plot_trace(trace_1, var_names=["w0", "w1"])

with pm.Model() as model_2:
    w0 = pm.Normal("w0", mu=0, sigma=10)
    w1 = pm.Normal("w1", mu=0, sigma=10)
    w2 = pm.Normal("w2", mu=0, sigma=10)
    e = pm.HalfCauchy("epsilon", 5)
    mu = pm.Deterministic("mu", w0 + w1*x + w2*x**2)
    y_pred = pm.Normal("y_pred", mu=mu, sigma=e, observed=y)
    trace_2 = pm.sample(1000, chains=2, cores=1)
az.plot_trace(trace_2, var_names=["w0", "w1", "w2"])

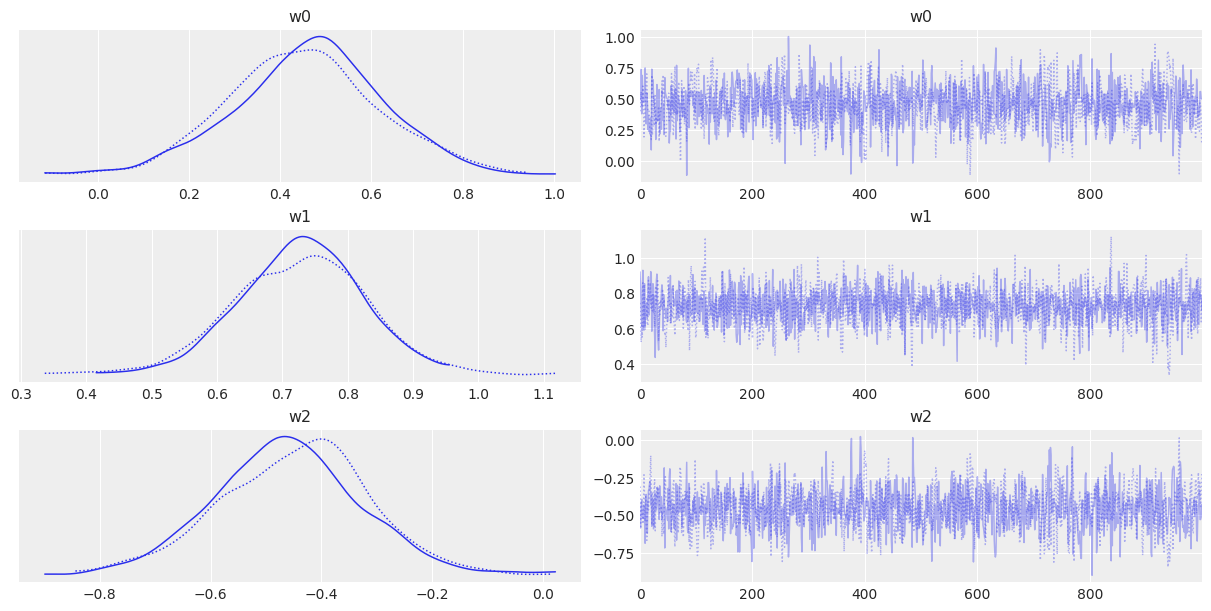
idx = np.argsort(x)
post_1_w0 = trace_1.posterior["w0"].values.reshape(-1)
post_1_w1 = trace_1.posterior["w1"].values.reshape(-1)
post_2_w0 = trace_2.posterior["w0"].values.reshape(-1)
post_2_w1 = trace_2.posterior["w1"].values.reshape(-1)
post_2_w2 = trace_2.posterior["w2"].values.reshape(-1)

sig_1 = az.hdi(trace_1.posterior, hdi_prob=0.90)["mu"].values[idx] 
sig_2 = az.hdi(trace_2.posterior, hdi_prob=0.90)["mu"].values[idx]

plt.scatter(x, y)
plt.plot(x[idx], np.mean(post_1_w0[idx])+np.mean(post_1_w1[idx])*x[idx], c="c")
plt.plot(x[idx], np.mean(post_2_w0[idx])+np.mean(post_2_w1[idx])*x[idx]+np.mean(post_2_w2[idx])*x[idx]**2, c="m")
plt.fill_between(x[idx], y1=sig_1[:,0], y2=sig_1[:,1], color="c", alpha=0.20)
plt.fill_between(x[idx], y1=sig_2[:,0], y2=sig_2[:,1], color="m", alpha=0.20)
plt.show()

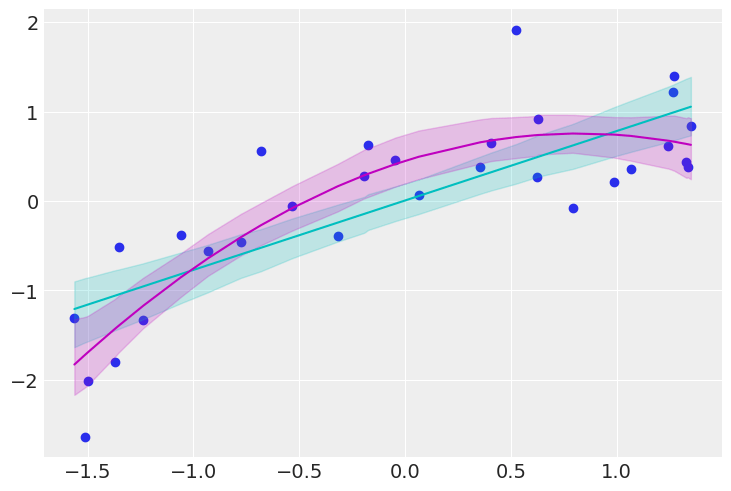
情報量基準を見る

pm.compute_log_likelihood(trace_1, model=model_1)
pm.compute_log_likelihood(trace_2, model=model_2)

print(az.waic(trace_1))
print(az.waic(trace_2))

df_comp_waic = az.compare({"model1": trace_1, "model2": trace_2})
az.plot_compare(df_comp_waic, insample_dev=False)

output

Computed from 2000 posterior samples and 30 observations log-likelihood matrix.

          Estimate       SE
elpd_waic   -31.16     4.15
p_waic        3.00        -

There has been a warning during the calculation. Please check the results.
Computed from 2000 posterior samples and 30 observations log-likelihood matrix.

          Estimate       SE
elpd_waic   -26.14     3.64
p_waic        3.61        -

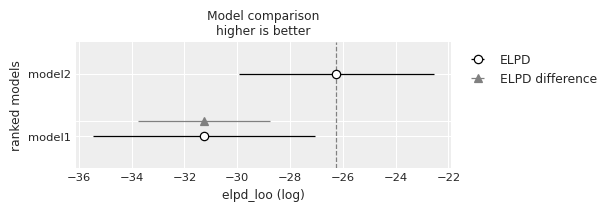
図の見方は以下のドキュメントのようになっている。最良のモデルは灰色の点線がつく。

https://www.pymc.io/projects/docs/en/stable/learn/core_notebooks/model_comparison.html
The empty circle represents the values of LOO and the black error bars associated with them are the values of the standard deviation of LOO.
The value of the highest LOO, i.e the best estimated model, is also indicated with a vertical dashed grey line to ease comparison with other LOO values.
For all models except the top-ranked one we also get a triangle indicating the value of the difference of WAIC between that model and the top model and a grey error bar indicating the standard error of the differences between the top-ranked WAIC and WAIC for each model.

情報量基準値の絶対値が小さいのは曲線モデルだった。これは直線モデルより良いモデルであることを示す。

情報量基準の解釈と使用方法

モデルの平均化 (model averaging): モデルセット $\{ \mathcal{M}_m \}$ を情報量基準でsoftmaxし加重平均する。

$$\begin{aligned} \mathcal{M}_{\text{ave}} &= \sum_{m=1}^{M} w_m \mathcal{M}(t|\bold{x}) \\ w_m &= \frac{e^{-\frac{1}{2 Δ\text{IC}_m}}}{\sum_{i}^{M} e^{-\frac{1}{2 Δ\text{IC}_i}}} \end{aligned}$$

$Δ\text{IC}_m$ はモデル $\mathcal{M}_m$ の情報量基準 $\text{IC}_m$ と最小の情報量基準 $\min(\{ \text{IC}_m\})$ の差。この方法により作られたメタモデルを使う方法が最も単純な使用方法になる。
他の方法として全ての $\mathcal{M}$ を含むスーパーモデルを明示的に構築するなどがある。

事後予測チェック

モデルにフィットさせたデータを用いて一致性をチェックする。

fig, axes = plt.subplots(1, 2, figsize=(10,3))
axes = axes.ravel()

for i in range(len(post_1_w0)):
    axes[0].scatter(x, post_1_w0[i] + post_1_w1[i]*x, color="c", alpha=0.25)
    axes[1].scatter(x, post_2_w0[i] + post_2_w1[i]*x + post_2_w2[i]*x**2, color="m", alpha=0.25)
axes[0].plot(x[idx], np.mean(post_1_w0[idx])+np.mean(post_1_w1[idx])*x[idx], c="c")
axes[1].plot(x[idx], np.mean(post_2_w0[idx])+np.mean(post_2_w1[idx])*x[idx]+np.mean(post_2_w2[idx])*x[idx]**2, c="m")
axes[0].scatter(x, y, color="b")
axes[1].scatter(x, y, color="b")
plt.show()

4. ベイズファクター

ベイズファクター(Bayes Factor): モデルが望ましい評価、比較する一般的な方法。ただし事前分布の形状には殆ど影響のないようなパラメータの数値に敏感で、さらにその計算は(代数的には)難解な問題がある。PyMCを使えば計算は勝手にしてくれる。

• 1 < BF 3: Anecdotal(言及するほどでもない)
• 3 < BF < 10: Substantial, Moderate, Positive(そこそこ)
• 10 < BF < 30: Positive, Strong(かなり望ましい)
• 30 < BF < 100: Very strong(非常に望ましい)
• 100 < BF: Decisive, Extreme(極端に望ましい)

https://www.pymc.io/projects/docs/en/v3.11.4/pymc-examples/examples/diagnostics_and_criticism/Bayes_factor.html

ベイズモデル比較

PRML 3.4

次の問題設定を考える。

• $M$ 個のモデルセット $\{ \mathcal{M}_m \}$ を比較する
• モデルは観測されたデータ $\mathcal{D}$ 上の確率分布 $p(\mathcal{M}_m|\mathcal{D})$ (多項式fittingを例では目標値 $\bold{t}$ の集合上に定義される分布)
• 入力値の集合 $\mathcal{X}$ は既知
• モデルの不確かさ $p(\mathcal{M}_m)$

この設定で、モデルの事後分布 $p(\mathcal{M}_m|\mathcal{D})$ はベイズの定理から、モデルの不確かさ $p(\mathcal{M}_m)$ とモデルエビデンス $p(\mathcal{D}|\mathcal{M}_m)$ の積に比例する。モデルエビデンスはデータから見たモデルの適切さを表し、モデル空間でモデルのパラメータを周辺化した尤度、周辺尤度 (maarginal likelihood)である。
ベイズファクターはこのモデルエビデンスの比、つまりモデルの適切さの比を示していると言え、分子のモデルが分母のモデルより優れていれば1以上の値になる。

設定より、事後分布 $p(\mathcal{M}_m|\mathcal{D})$ が得られているので予測分布が以下のように計算でき、これは混合分布 (mixture distribution)の一種になる。

$$p(t|\bold{x},\mathcal{D}) = \sum_{m=1}^{M} p(t|\bold{x},\mathcal{M}_m,\mathcal{D}) p(\mathcal{M}_m|\mathcal{D})$$

混合分布なので、全体の予想分布が、個々のモデルの予測分布 $p(t|\bold{x},\mathcal{M}_m,\mathcal{D})$ の、事後確率 $p(\mathcal{M}_m|\mathcal{D})$ による期待値として計算できる。つまりモデル平均化である。例えば同じく単峰性の予測分布を持つがその中心 $μ_1, μ_2$ が異なる $\mathcal{M}_1$ と $\mathcal{M}_1$ がある時、全体の予測分布は多峰性の分布になり、 $μ_1, μ_2$ の2箇所に最頻値を持つ予測分布になる。

といいつつ、最も単純明快なモデル平均は $\mathcal{M}_m$ を1つだけを選び他は捨ててしまう方法で、これはモデル選択 (model selection)という。
1つのパラメータ $w$ を持つモデル $\mathcal{M}_m$ のモデルエビデンスは周辺尤度より次になる。

$$p(\mathcal{D}|\mathcal{M}_m) = \int p(\mathcal{D}|w,\mathcal{M}_m) p(w,\mathcal{M}_m) dw$$

周辺尤度は「パラメータを事前分布からサンプリングした時に手元にある $\mathcal{D}$ を再現できる確率」といえる。そしてこれは事後分布計算するときに分母に現れる正規化定数である。

$$p(w|\mathcal{D},\mathcal{M}_m) = \frac{ p(\mathcal{D}|w,\mathcal{M}_m) p(\bold{w},\mathcal{M}_m) }{ p(\mathcal{D}|\mathcal{M}_m) }$$

次の設定を考えることで、モデルエビデンスを変形して、表現力と複雑さを分離して示すことを考える。

• 事後分布が最頻値 $w_{\text{MAP}}$ 近傍で尖っていて、その幅は $Δw_{\text{post}}$
• 事前分布は大きく平べったい一様分布として、その幅は $Δw_{\text{prior}}$
• これらを長方形で近似し、面積 $Δw_{\text{post}} × p(w_{\text{MAP}}|\mathcal{D},\mathcal{M}_m)$ と $Δw_{\text{prior}} × p(w|\mathcal{M}_m)$
• 分布は面積の総和が1になるので $p(w|\mathcal{M}_m) = \frac{1}{Δw_{\text{prior}}}$

以上の設定から、事後分布を $w$ で積分し $w$ を消すことで次のようになる。

$$\begin{aligned} \int p(w|\mathcal{D},\mathcal{M}_m) dw & ≈ p(w_{\text{MAP}}|\mathcal{D},\mathcal{M}_m) Δw_{\text{prior}} \\ & = \frac{ p(\mathcal{D}|w,\mathcal{M}_m) p(\bold{w},\mathcal{M}_m) }{ p(\mathcal{D}|\mathcal{M}_m) } Δw_{\text{prior}} \\ & ↓ × p(\mathcal{D}|\mathcal{M}_m) \\ \int p(w|\mathcal{D},\mathcal{M}_m) p(\mathcal{D}|\mathcal{M}_m) dw &≈ p(\mathcal{D}|w,\mathcal{M}_m) p(\bold{w},\mathcal{M}_m) Δw_{\text{prior}} \\ & ↓ (p(\bold{w},\mathcal{M}_m) = \frac{1}{Δw_{\text{prior}}}) \\ & = p(\mathcal{D}|w,\mathcal{M}_m) \frac{Δw_{\text{prior}}}{Δw_{\text{prior}}} \\ & = p(\mathcal{D}|w_{\text{MAP}},\mathcal{M}_m) \frac{Δw_{\text{prior}}}{Δw_{\text{prior}}} \end{aligned}$$

$$\begin{aligned} p(\mathcal{D}|\mathcal{M}_m) & = \int p(w|\mathcal{D},\mathcal{M}_m) dw \\ & ≈ p(\mathcal{D}|w_{\text{MAP}},\mathcal{M}_m) \frac{Δw_{\text{prior}}}{Δw_{\text{prior}}} \\ \ln p(\mathcal{D}|\mathcal{M}_m) & ≈ \ln p(\mathcal{D}|w_{\text{MAP}},\mathcal{M}_m) + \ln (\frac{Δw_{\text{prior}}}{Δw_{\text{prior}}}) \\ & ↓ (w → \bold{w} \in \mathbb{R}^{C}) \\ & = \ln p(\mathcal{D}|\bold{w}_{\text{MAP}},\mathcal{M}_m) + C \ln (\frac{Δw_{\text{prior}}}{Δw_{\text{prior}}}) \end{aligned}$$

以上の変形で対数モデルエビデンスは次の2項に分けられる。

• 最適なパラメータのときのデータへのfit具合。(通常モデルが複雑だと一般にはfitしやすくなる)(事前分布が一様分布の場合の対数尤度に相当)
• 事前分布に対して事後分布がデータに強くfitしすぎる場合の正則化。( $\frac{Δw_{\text{prior}}}{Δw_{\text{prior}}}$ は大きさの関係から常に0~1なので対数は負値を取る)
• パラメータ数 $c$ が多いと正則化が強くなる。

これを解釈すると、バランスがいいモデル選択が次の方法でできることが理解できる。

1. まず事前分布 $p(\bold{w}|\mathcal{M}_m)$ からパラメータ $\bold{w}$ をドロー
2. ドローした $\bold{w}$ に対して $p(\mathcal{D}|\bold{w},\mathcal{M}_m)$ からデータをサンプリング

• 単純なモデルは自由度が少ないので生成されるデータは多様性に乏しく、そのデータの分布 $p(\mathcal{D}|\mathcal{M}_m)$ は狭い範囲に集中する。
• 逆に複雑なモデルはデータの分布が多様で $p(\mathcal{D}|\mathcal{M}_m)$ は広い範囲に散らばる。

3. $\{ \mathcal{M} \}$ の中に正解のモデルがあると仮定すると、その中程度の複雑さのモデルが生成したデータはある $\mathcal{D}_d$ に対してエビデンスが高くなる。(???)

PyMCでの計算

ベイズファクターの計算は階層モデルとして定式化できる。複数の競合したモデルに対して同時に推論を行い、モデル間の離散変数を使う。

$$\begin{aligned} \text{BF} & = \frac{p(t|\mathcal{M}_0)}{p(t|\mathcal{M}_1)} \\ & = \frac{p(\mathcal{M}_0|t) p(\mathcal{M}_1)}{p(\mathcal{M}_1|t) p(\mathcal{M}_0)} \end{aligned}$$

分数部分がオッズであることに注意。

# コイン投げモデル2つを比較する

coins = 100
heads = 32
y_d = np.repeat([0, 1], [coins-heads, heads])  # shape [36]
# -> [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]

# ここでは事前分布のみ異なるモデルを比較するが、尤度など他のものが異なるものでも可能
with pm.Model() as model:
    p = np.array([0.5, 0.5])
    midx = pm.Categorical("midx", p=p)
    m0 = pm.Beta("model0", alpha=4, beta=8) 
    m1 = pm.Beta("model1", alpha=8, beta=4)
    theta = pm.Deterministic("theta", pm.math.switch(pm.math.eq(midx, 0), m0, m1))  # switch: if arg0 then arg1 else arg2
    y = pm.Bernoulli("y_pred", p=theta, observed=y_d)

    trace = pm.sample(2000, chains=2, cores=1)

az.plot_trace(trace, var_names=["midx", "model0", "model1", "theta"])
az.plot_autocorr(trace, var_names=["midx", "model0", "model1", "theta"], combined=True)

pm1 = trace.posterior["midx"].values.mean()
pm0 = 1 - pm1
bf = (pm0*p[1])/(pm1*p[0])  # p(M0|t)p(M1)/p(M1|t)p(M0)
print(f"{pm0} {pm1}, {bf}")

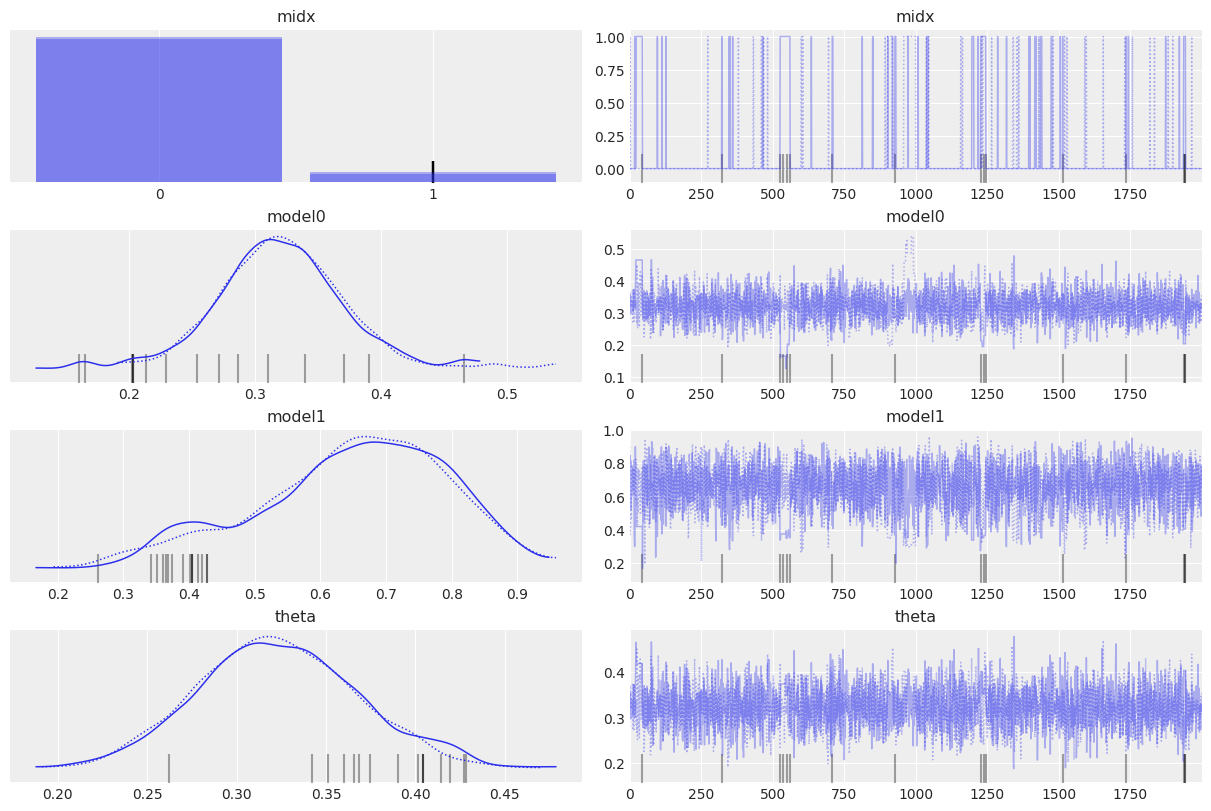
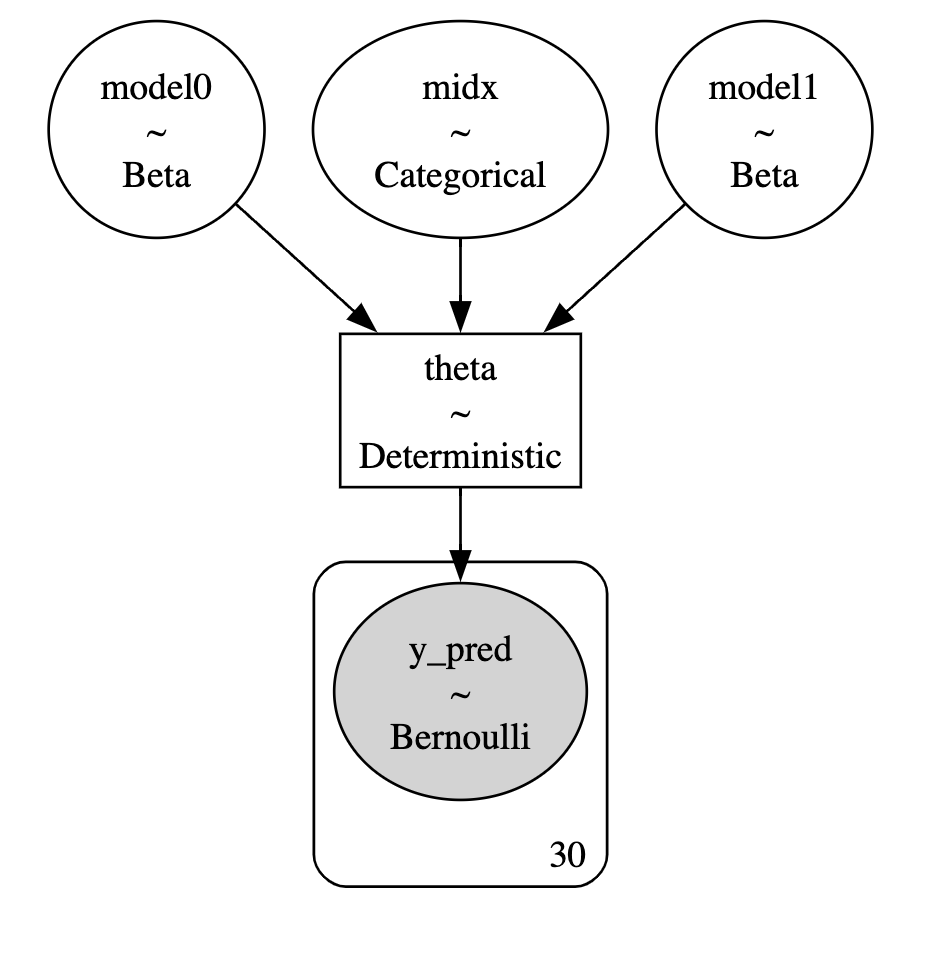
model0のベイズファクターが15ほどになり、これはmodel1より望ましいモデルであることを示している。

5. ベイズファクターと情報量基準

ベイズ主義者がベイズファクターを好まない理由として事前分布に対して敏感過ぎる点がある。
ベイズファクターや情報量基準が何をしているか見てみる。

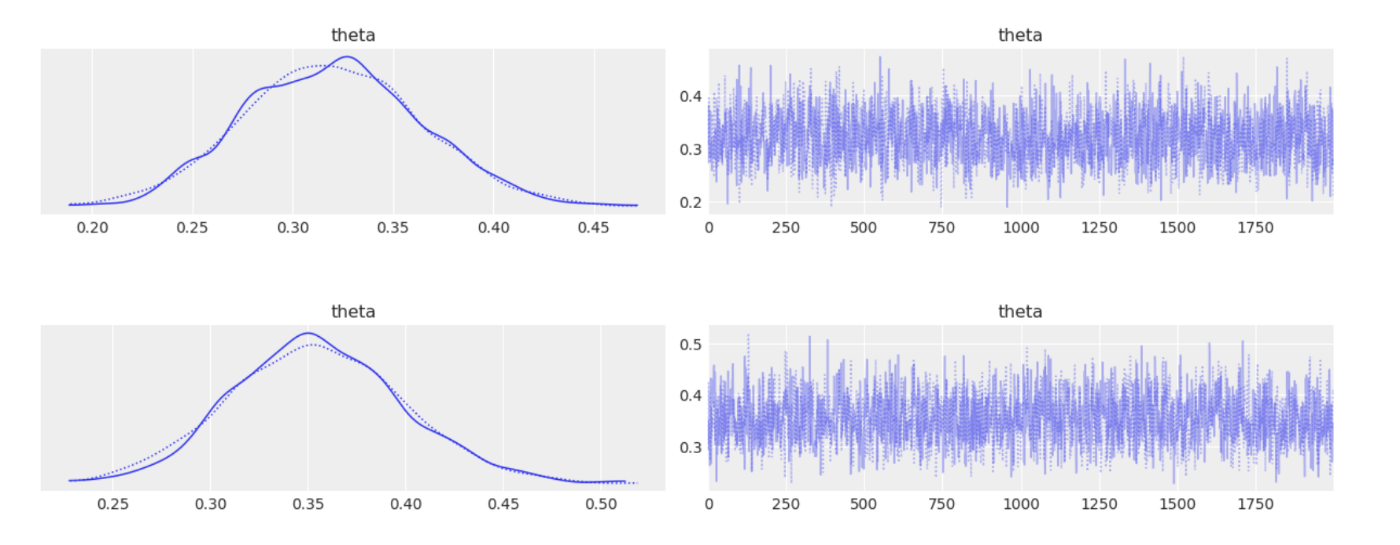
次の2つのモデルは異なる事前分布を持つが、事前分布の効果が無視できるほど多くのデータを持っていることにより同じような分布に収束している。

with pm.Model() as model_bf0:
    theta = pm.Beta("theta", alpha=4, beta=8) 
    y = pm.Bernoulli("y_pred", p=theta, observed=y_d)
    trace_bf0 = pm.sample(2000, chains=2, cores=1)
az.plot_trace(trace_bf0, var_names=["theta"])

with pm.Model() as model_bf1:
    theta = pm.Beta("theta", alpha=8, beta=4) 
    y = pm.Bernoulli("y_pred", p=theta, observed=y_d)
    trace_bf1 = pm.sample(2000, chains=2, cores=1)
az.plot_trace(trace_bf1, var_names=["theta"])

post_bf0 = trace_bf0.posterior["theta"].values.mean(axis=0)
post_bf1 = trace_bf1.posterior["theta"].values.mean(axis=0)
print(post_bf0.mean(), post_bf1.mean())

pm.compute_log_likelihood(trace_bf0, model=model_bf0)
pm.compute_log_likelihood(trace_bf1, model=model_bf1)

print(az.waic(trace_bf0))
print(az.waic(trace_bf1))

df_comp_waic = az.compare({"model1": trace_bf0, "model2": trace_bf1})
az.plot_compare(df_comp_waic, insample_dev=False)

output

Computed from 4000 posterior samples and 100 observations log-likelihood matrix.

          Estimate       SE
elpd_waic   -63.62     3.59
p_waic        0.93        -
Computed from 4000 posterior samples and 100 observations log-likelihood matrix.

          Estimate       SE
elpd_waic   -63.79     2.84
p_waic        0.83        -

情報量基準的には、データ数が多いので事前分布の効果が薄れて同じモデルになっているのがわかる。

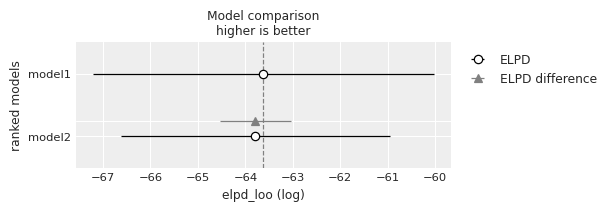
ベイズファクターの計算では、モデルが殆ど同じ推論を行っていたとしても、事前分布の適合の良さでいいモデルを選ぶことができる。
情報量基準では、データを増やしてモデルの相対的な差が小さくなると、 $θ$ の推定値も似てくることにより、両モデルの評価はおなじになってくる。

感想

モデルの複雑さについての直感的な理解を、PyMCの実装とPRMLの理論面を両方得られた。でもPRMLのほうは何回読んでも難しい。
情報量基準、特に最近よく聞くWAICについてはある程度自前で求めることができるようになったが、ベイズファクターについては教科書のモデル以外では自作できるか怪しい。もう少し馴染んでおかないと実用できないと思う。

twitter(旧X)でベイズの人がベイズファクター推しだったので、この本ではあまり人気がないと言われている部分は実感がない。実際確かに事前分布までみてモデルを選ぶという意味では高度でいいと思うが、事後分布として同じに収束したならそれで良いのでは...?という感じがする。実用ではどうなのだろうか。