Bayesian Analysis with PyMC 勉強ノート 8 ガウス過程
Osvaldo Martin 著, 金子武久 訳
Pythonによるベイズ統計モデリング (Bayesian Analysis with Python)
2018-06-26
https://www.kyoritsu-pub.co.jp/book/b10003944.html
Christopher M. Bishop 著, 元田浩 栗田多喜夫 樋口知之 松本裕治 村田昇 監訳
パターン認識と機械学習 ベイズ理論による統計的予測 (Pattern Recognition and Machine Learning)
2012-01-20
https://www.maruzen-publishing.co.jp/item/?book_no=294524
Pythonによるベイズ統計モデリングを読んだので学習メモを整理します。学習中のノートなので正確ではないかもしれません。使われているコードをPyMC3からPyMC5に書き直しました。
また、せっかくなのでPRMLの本を参照しながら読むことにしました。式の文字の扱いなどはPRML風になるよう頭に収めようと思っています。
ガウス過程
ノンパラメトリック(non-parametetric)モデルを使うことで、データとともにパラメータ数、つまりモデルの複雑さが適応的に変わる。
カーネル回帰とガウス過程について学び、正規分布の無限次元への拡張と関数の分布(distribution of function)を最適化する方法から説き起こすことでパラメータ付きカーネルが諸関数の推論を可能にすることを理解する。
次のライブラリを使用する。
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
import pymc as pm
import pytensor
import arviz as az
az.style.use("arviz-darkgrid")
1. ノンパラメトリック統計学
ベイズ的な視点で、ノンパラメトリックモデルはデータサイズによってパラメータ数が大きくなるモデルとして定義できる。モデルの無限個のパラメータを、データによって有限個に抑える。つまりパラメータ数を規定するためにデータを使うといえる。
通常のパラメトリックモデルでは、入力(独立変数、予測変数、説明変数)
メモリベース法(memory-based method): 学習データとテストデータを推論時に両方使う方法。 e.g. Parzen推定
しかしメモリベースでは推論にも大きなコストがかかる悪さもある。
カーネルベースモデル
PRML 6.3
線形モデルは同値な双対表現(dual representation)で書き直すことができて、推論は訓練データを中心に定義されるカーネル関数(kernel function)の線形結合で計算される。予め設定しておく特徴空間への写像
SVMを習った人なら有名な話かもしれない。
線形カーネルは
-
不変カーネル(stationary kernel): 引数の差
\bold{x}_1 - \bold{x}_2 - RBF(radial basis function): 2つの引数間の距離にのみ依存するカーネル。
以下では線形モデルを、誤差関数
ここで
これを
これを予測
内積部分が全てがカーネル関数で表せるので、
最も人気があるのはガウスカーネル で、無限次元の特徴空間に対応している。
2. カーネル回帰
まず、線形回帰の定式化を思い出す。
ここで、基底関数
この
データ点にノットが近いほどRBFカーネルは大きな値を返す、つまり類似度を示す値になる。
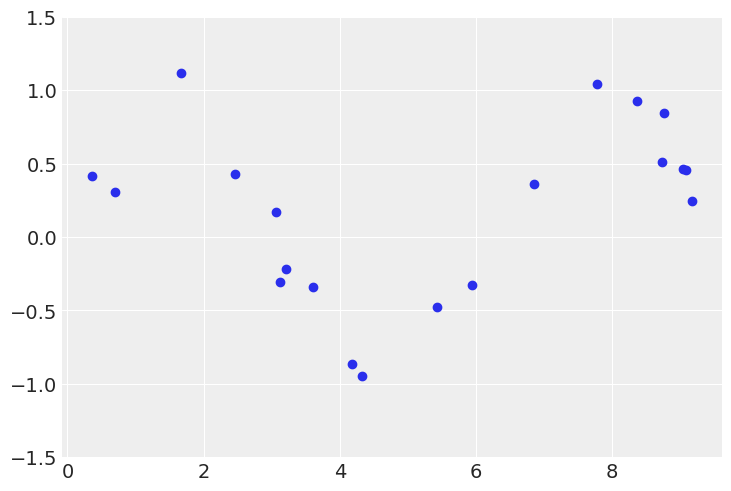
これを示すため、グリッドアプローチで、グリッド点
# sin曲線からノイズ付き観測点をドローする
x = np.random.uniform(0, 10, size=20)
x = x[np.argsort(x)]
y = np.random.normal(np.sin(x), scale=0.2)
plt.scatter(x, y)
plt.ylim(-1.5, 1.5)
# RBFカーネル
def kernel(x, n, sigma=1):
knot = np.linspace(x.min(), x.max(), n)
return np.array([np.exp(-(x-k)**2 / (2*sigma**2)) for k in knot])
# カーネル回帰
n_knot = 5
with pm.Model() as model:
gamma = pm.Cauchy("gamma", alpha=0, beta=1, shape=n_knot)
eps = pm.HalfCauchy("eps", beta=5)
mu = pm.math.dot(gamma, kernel(x, n_knot))
y_pred = pm.Normal("y_pred", mu=mu, sigma=eps, observed=y)
trace = pm.sample(1000, chains=2, cores=1)
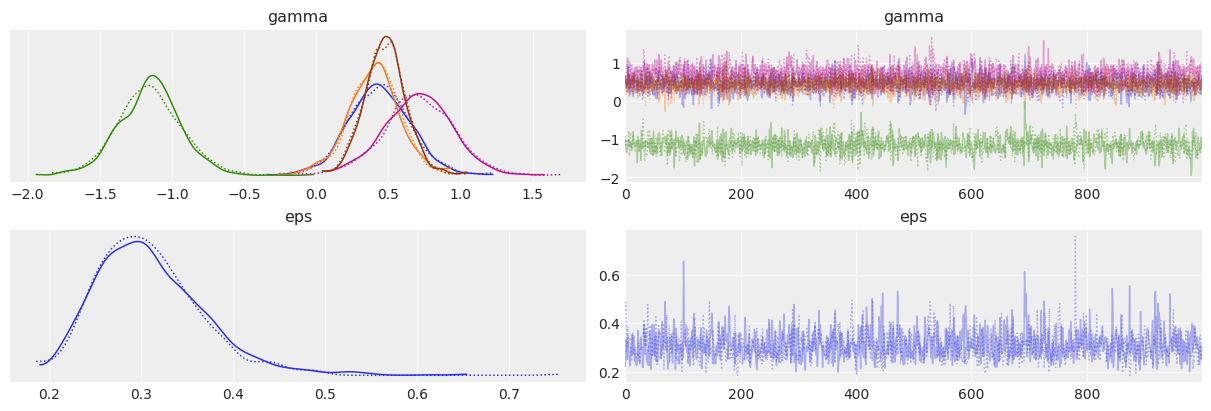
az.plot_trace(trace, var_names=["gamma", "eps"])
az.plot_autocorr(trace, var_names=["gamma", "eps"], combined=True)
az.summary(trace, var_names=["gamma", "eps"])

# 事後予測チェック
ppc = pm.sample_posterior_predictive(trace, model=model)
fig, axes = plt.subplots(1, 2, figsize=(10,4))
axes[0].plot(x, ppc.posterior_predictive["y_pred"].values.mean(axis=0).T, "ro", color="r", alpha=0.005)
axes[0].scatter(x, y, color="b")
axes[0].set_ylim(-1.5, 1.5)
x_new = np.linspace(x.min(), x.max(), 100)
k = kernel(x_new, n_knot)
gamma_pred = trace.posterior["gamma"].values.mean(axis=0)
for _ in range(100):
idx = np.random.randint(0, len(gamma_pred))
y_ppc = np.dot(gamma_pred[idx], k)
axes[1].plot(x_new, y_ppc, "r-", alpha=0.1)
axes[1].set_ylim(-1.5, 1.5)
axes[1].scatter(x, y, color="b")
fig.show()
az.plot_ppc(ppc, num_pp_samples=20)


確かにデータ点同士を補完できている。
カーネル回帰における明らかな問題はノットの数と位置の選び方。
これを解決するアプローチとして次のアイディアがある。
- ノットとしてデータ点を使い、各データ点で正規分布を置きKDEのグラフを作る。
- ノットの位置をモデリングの中で決定されるようにする。(高難易度)
- 変数選択でモデリングの中にindex変数を取り込む。(indexの組み合わせ爆発があるので低次元な問題しか扱えない)
RBFを考えるモチベーションとして、目的変数ではなく入力変数
2つの導出方法がある。(個人的にはNadaraya-Watsonの方法がわかりやすかった)
RFBネットワークの方法
ノイズ
変分の必要条件のメモ: これを満たす
Nadaraya-Watsonの方法
カーネル密度推定の観点からアプローチする。(PRML 2.5.1)
訓練データ
回帰関数
3. ガウス過程
PRML 6.4
関数空間の中で直接推論を行うもう一つの方法、ガウス過程(Gaussian Process; GP)を使う。ガウス過程による回帰の一種として自己回帰移動平均モデルやカルマンフィルタ、前述のRFBネットワークなどがある。
カーネルを確率的識別モデルへ適用することでガウス過程を導出すれば、ベイズ的にも自然にカーネルが現れることを以下で見ていく。
ガウス過程から線形回帰を見る
通常のベイズ的な線形回帰では、まず
以下では、ガウス過程がパラメトリックな推定を経ずに関数の事前分布を直接定義する ことを説明するために、事前分布
まず、
ここで特徴の計画行列
双対表現の章で見た通り、
おそらく、この式変形こそがガウス過程が線形回帰を上手くfitできることのコアで、特徴を与える基底関数の積であるカーネルをパラメータとすることによって、回帰関数そのものの事前分布を与えられられること が一目瞭然である。感動した。
確率過程(stochastic process): 確率過程
嬉しいことに、ガウス過程は全てが平均と共分散という2次統計量で記述できていて、実用でも平均は0で扱う事が多い(
以上の議論でガウス過程がなぜ柔軟な関数系を描けるかについて、特徴を与える基底関数をカーネルという形で記述できたことで、これを事前分布から選んでいるからだとわかった。
カーネル関数は基底関数を定義して決めることもできるが、RBFカーネルや指数カーネルなどで直接与えることもできる。特に指数カーネルの場合はOrnstein-Uhlenbeck過程 としてブラウン運動の記述などで使うらしい。
次に、実際の回帰タスクでどのように予測分布を与えるのかについて見ていく。
以下では、観測される目標変数に含まれるノイズを考えることから始めて、事前分布と尤度の定義、それから得られる周辺分布の共分散、そしてその共分散により導かれる予測分布の平均と分散を確認して、「カーネルを成分に持つ予測分布の共分散
次の順番で設定が一覧できる。
-
t_n = y(\bold{x}_n) + ε -
p(t_n|y(\bold{x}_n)) = \mathcal{N}(t_n | y(\bold{x}_n), β^{-1}) β -
p(\bold{t}|\bold{y}) = \mathcal{N}(\bold{t} | \bold{y}, β^{-1}\bold{I}_N) y ε -
p(\bold{y}) = \mathcal{N}(\bold{y} | \bold{0}, \bold{K}) \bold{y} -
p(\bold{t}) = \mathcal{N}(\bold{t} | \bold{0}, \bold{C}) \bold{t} p(\bold{t}|\bold{y}) -
[\bold{C}]_{n,m} = k(\bold{x}_n, \bold{x}_m) + β^{-1}δ_{n,m} δ fill_diagonal)。y ε -
k(\bold{x}_n, \bold{x}_m) = η e^{-\frac{ρ}{2} ||\bold{x}_n - \bold{x}_m||} + θ_0 + θ_1 \bold{x}_n^\top \bold{x}_m
-
これらを使って、「データ点の集合上での同時分布をモデル化する」というガウス過程の考えを、「訓練データ集合
まず
このブロック化された共分散行列を使って条件付き分布
ここで
注意としては、逆行列の計算は3乗オーダーかかるのでデータ点が多いと耐えられない。近似手法として以下のようなものがあり、高速化もされている。
概要のわかりやすい解説
PRML 6.4.3ではハイパラ
PyMCによる実装
まず最初にカーネル
def sqdistance(x_1, x_2):
return np.array([ [(x_1[i]-x_2[j])**2 for i in range(len(x_1))] for j in range(len(x_2)) ])
fig, axes = plt.subplots(1, 2, figsize=(10,3))
# GP事前分布から8個の関数を可視化してみる
points = np.linspace(0, 10, 100)
cov = np.exp(-sqdistance(points, points))
axes[0].plot(points, stats.multivariate_normal.rvs(cov=cov, size=8).T) # random val sample from multivariate-Normal
# さらに、GP事前分布からパラメータを定めて8個の関数を可視化する
eta = 1
rho = 0.1
sigma = 0.01
dist = sqdistance(points, points)
diag = eta + sigma
cov = eta * np.exp(-rho * dist)
np.fill_diagonal(cov, diag) # fill in the matrix "cov" with the val of "diag"
axes[1].plot(points, stats.multivariate_normal.rvs(cov=cov, size=8).T)
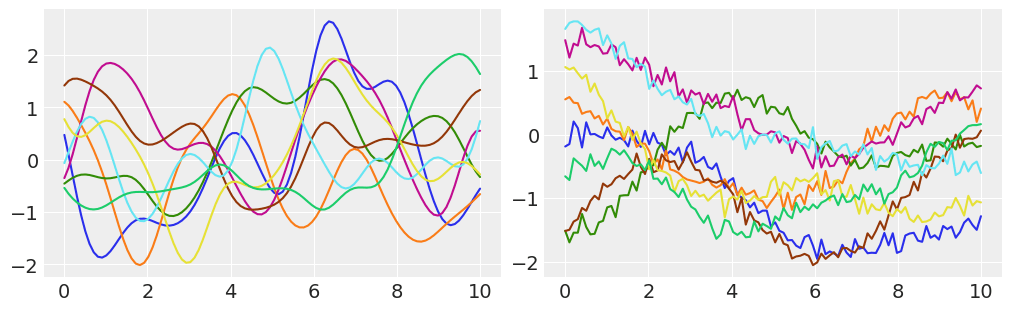
ガウスカーネルを持ったGP事前分布は、0を中心とした多数の滑らかな関数で構成されているのがわかる。(BAwP code 8.6はそのままだと動かず、8.7も図のとおりにはならなかった。この記事の実行結果は指数カーネルの挙動に近い。)
それでは事後予測分布の関数をサンプルしてみる。変数名はBAwPの流儀を少し入れているため、式は次の読み替えを行った。
-
y: 目標変数t -
sigma: 予測分布の共分散行列[\bold{C}]_{n,m} = k(\bold{x}_n, \bold{x}_m) + β^{-1}δ_{n,m} β^{-1} -
dist: 新しい点\bold{x}_{N+1} ||\bold{x}_n - \bold{x}_m|| k_ooの指数部分でつかう。 -
dist_x: 訓練データ\{ \bold{x}_n \} k_xの指数部分で使う。 -
diag_x:η+βδ_{n,m} k_xの対角成分。 -
dist_off_diag: 訓練データと新しい点の距離部分。k_oの指数部分で使う。 -
k_x:μ(\bold{x}_{N+1}) = \bold{k}^\top \bold{C}_N^{-1} \bold{t} \bold{C}_N -
k_o:\bold{k} η e^{-ρ ||\bold{x}_n - \bold{x}_m||} -
k_oo:c_{N+1 \dots,N+1 \dots} η e^{-ρ ||\bold{x}_{N+1 \dots} - \bold{x}_{N+1 \dots}||} -
post_mu:μ(\bold{x}_{N+1}) = \bold{k}^\top \bold{C}_N^{-1} \bold{t} \bold{K}_{\texttt{oo}}^\top \bold{K}_{\texttt{x}}^{-1} \bold{t} -
post_sigma:σ^2 (\bold{x}_{N+1}) = c_{N+1 \dots,N+1 \dots} - \bold{k}^\top \bold{C}_N^{-1} \bold{k} \bold{K}_{\texttt{oo}} - \bold{K}_{\texttt{o}}^\top \bold{K}^{-1} \bold{K}_{\texttt{o}}
逆行列の精度を良くするためにはコレスキー分解を使う方法もある。ここでは単純に逆行列をもとめている。
# 逆行列による計算を使ったGP
eta = 1
rho = 0.5
sigma = 0.03
points = np.linspace(0, 10, 100)
x = np.random.uniform(0, 10, size=20)
x = x[np.argsort(x)]
y = np.random.normal(np.sin(x), scale=0.2)
dist = sqdistance(points, points)
k_oo = eta * np.exp(-rho*dist)
dist_x = sqdistance(x, x)
k_x = eta * np.exp(-rho*dist_x)
diag_x = eta + sigma
np.fill_diagonal(k_x, diag)
dist_off_diag = sqdistance(x, points)
k_o = eta * np.exp(-rho*dist_off_diag)
mu_post = np.dot(np.dot(k_o, np.linalg.inv(k_x)), y)
sigma_post = k_oo - np.dot(np.dot(k_o, np.linalg.inv(k_x)), k_o.T)
plt.plot(points, stats.multivariate_normal.rvs(mean=mu_post, cov=sigma_post, size=100).T, color="r", alpha=0.05)
plt.scatter(x, y, color="b")
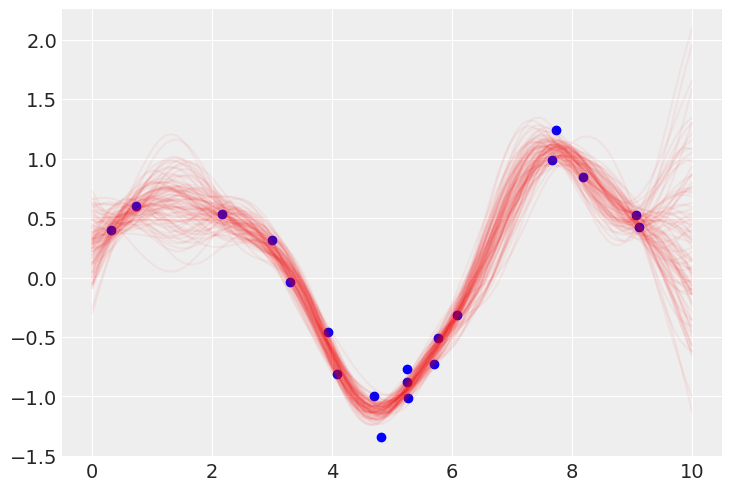
以上がガウス過程による回帰の数値計算である。
ハイパラメータの学習
決め打ちだった
(PRML上では
# PyMCによるコードの書き換え
# GP prior: f(x) ~ GP(μ=[0...0], k(x_1,x_2))
# likelyhood: p(y|x,f(x)) ~ N(f, σ^2 I)
# GP posterior: p(f(x)|x,y) ~ GP(μ_post, Σ_post)
N = 20
with pm.Model() as model:
mu = np.zeros(N)
eta = pm.HalfCauchy("eta", 5)
rho = pm.HalfCauchy("rho", 5)
sigma = pm.HalfCauchy("sigma", 5)
dist = sqdistance(x, x)
k_x = pytensor.tensor.extra_ops.fill_diagonal(eta * pm.math.exp(-rho * dist), eta+sigma)
obs = pm.MvNormal("obs", mu=mu, cov=k_x, observed=y)
point = np.linspace(0, 10, 100)
dist_pred = sqdistance(points, points)
dist_off_diag = sqdistance(x, points)
k_oo = eta * pm.math.exp(-rho * dist_pred)
k_o = eta * pm.math.exp(-rho * dist_off_diag)
mu_post = pm.Deterministic("mu_post", pm.math.dot(pm.math.dot(k_o, pytensor.tensor.nlinalg.matrix_inverse(k_x)), y))
sigma_post = pm.Deterministic("sigma_post", k_oo - pm.math.dot(pm.math.dot(k_o, pytensor.tensor.nlinalg.matrix_inverse(k_x)), k_o.T))
trace = pm.sample(1000, chains=2, cores=1)
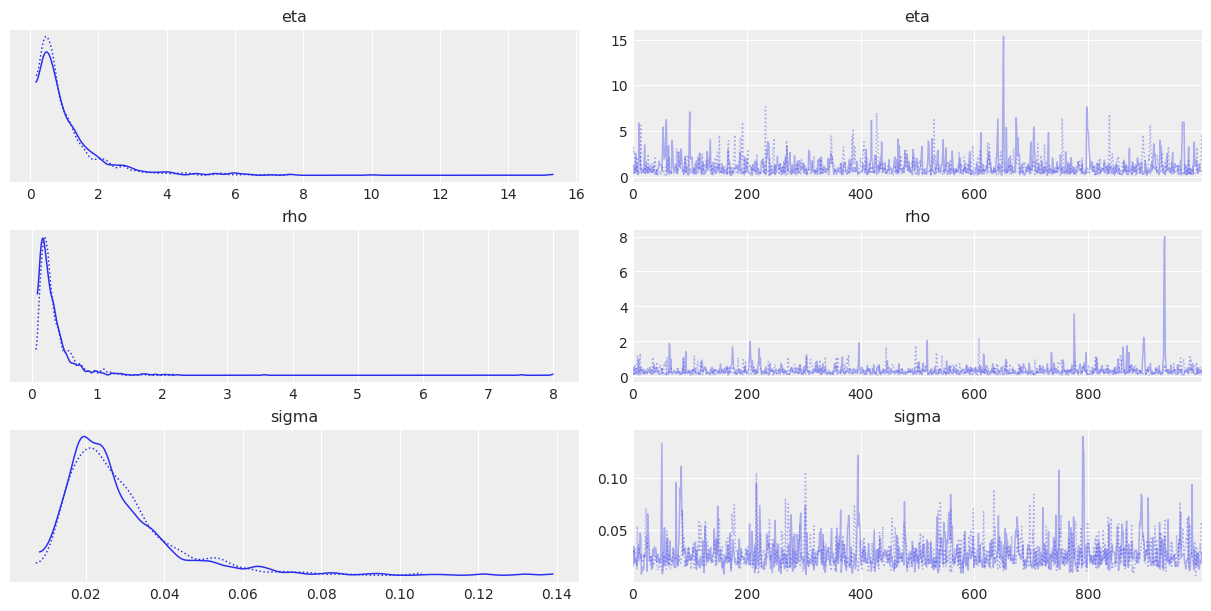
az.plot_trace(trace, var_names=["eta", "rho", "sigma"])
az.summary(trace, var_names=["eta", "rho", "sigma"])
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
eta 1.100 1.083 0.151 2.812 0.037 0.026 1025.0 1078.0 1.0
rho 0.342 0.355 0.084 0.768 0.012 0.008 1018.0 1031.0 1.0
sigma 0.028 0.014 0.009 0.054 0.000 0.000 1045.0 1192.0 1.0
# 事後予測チェック
trace_mu_post = trace.posterior["mu_post"].values.mean(axis=0)
trace_sigma_post = trace.posterior["sigma_post"].values.mean(axis=0)
y_pred = [np.random.multivariate_normal(mean=m, cov=s) for m,s in zip(trace_mu_post, trace_sigma_post)]
for yp in y_pred:
plt.plot(points, yp, color="r", alpha=0.05, zorder=1)
plt.scatter(x, y, color="b", zorder=2)
plt.show()
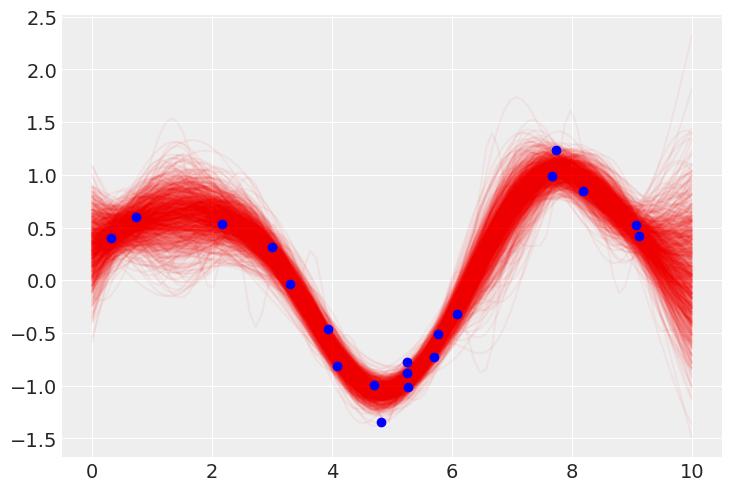
以上でMCMCで最適化されたガウス過程の回帰が可能になったことがわかる。
しかし、今回のデータは周期性があるという事前知識があるので、カーネルに周期性の情報を与えて外挿における不確実性を減らすこともできる。
# 周期カーネルを用いた場合
def periodic_distance(x_1, x_2):
return np.array([ [np.sin( (x_1[i]-x_2[j])/2 )**2 for i in range(len(x_1))] for j in range(len(x_2)) ])
N = 20
with pm.Model() as model:
mu = np.zeros(N)
eta = pm.HalfCauchy("eta", 5)
rho = pm.HalfCauchy("rho", 5)
sigma = pm.HalfCauchy("sigma", 5)
dist = periodic_distance(x, x)
k_x = pytensor.tensor.extra_ops.fill_diagonal(eta * pm.math.exp(-rho * dist), eta+sigma)
obs = pm.MvNormal("obs", mu=mu, cov=k_x, observed=y)
point = np.linspace(0, 10, 100)
dist_pred = periodic_distance(points, points)
dist_off_diag = periodic_distance(x, points)
k_oo = eta * pm.math.exp(-rho * dist_pred)
k_o = eta * pm.math.exp(-rho * dist_off_diag)
mu_post = pm.Deterministic("mu_post", pm.math.dot(pm.math.dot(k_o, pytensor.tensor.nlinalg.matrix_inverse(k_x)), y))
sigma_post = pm.Deterministic("sigma_post", k_oo - pm.math.dot(pm.math.dot(k_o, pytensor.tensor.nlinalg.matrix_inverse(k_x)), k_o.T))
trace = pm.sample(1000, chains=2, cores=1)
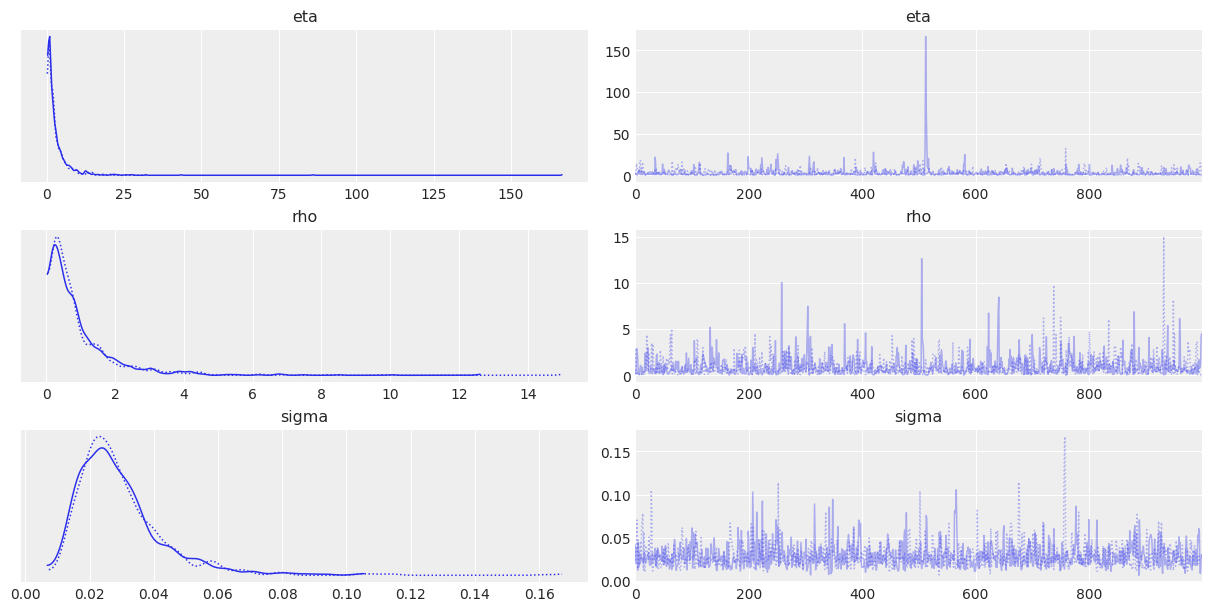
az.plot_trace(trace, var_names=["eta", "rho", "sigma"])
az.summary(trace, var_names=["eta", "rho", "sigma"])
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
eta 3.042 5.434 0.117 8.735 0.204 0.145 814.0 1093.0 1.0
rho 0.942 1.091 0.019 2.673 0.033 0.023 904.0 926.0 1.0
sigma 0.029 0.014 0.011 0.055 0.000 0.000 1275.0 1086.0 1.0
trace_mu_post = trace.posterior["mu_post"].values.mean(axis=0)
trace_sigma_post = trace.posterior["sigma_post"].values.mean(axis=0)
y_pred = [np.random.multivariate_normal(mean=m, cov=s) for m,s in zip(trace_mu_post, trace_sigma_post)]
for yp in y_pred:
plt.plot(points, yp, color="r", alpha=0.05, zorder=1)
plt.scatter(x, y, color="b", zorder=2)
plt.show()
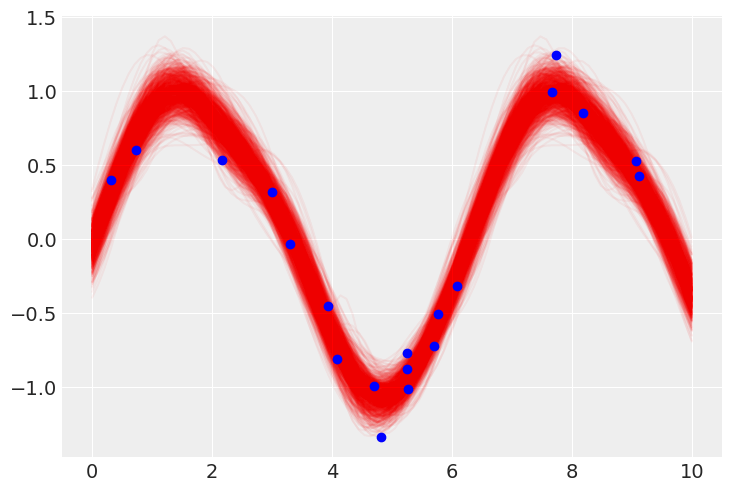
周期性を捉え、2乗距離カーネルよりも不確実性が小さくなっている。
PyMCネイティブなGP
共分散の定め方に関してはこのページが日本語でわかりやすかった。
# 事前分布 k_prior
fig, axes = plt.subplots(1, 2, figsize=(10,4))
points = np.linspace(0, 10, 100)[:, None] # -> shape [100, 1]
sig = 1.0
cov = pm.gp.cov.ExpQuad(input_dim=1, ls=sig) # L2 kernel
cov += pm.gp.cov.WhiteNoise(1e-6)
k_prior = cov(points).eval() # \bold{C}_N
axes[0].plot(points, pm.draw(pm.MvNormal.dist(mu=np.zeros(len(k_prior)), cov=k_prior, shape=k_prior.shape[0]), draws=5).T)
sig = 1.0
cov = pm.gp.cov.Periodic(1, period=5.0, ls=sig) # periodic kernel
cov += pm.gp.cov.WhiteNoise(1e-6)
k_prior = cov(points).eval()
axes[1].plot(points, pm.draw(pm.MvNormal.dist(mu=np.zeros(len(k_prior)), cov=k_prior, shape=k_prior.shape[0]), draws=5).T)

周期カーネルの共分散行列を使うと、gp.conditional内の積でXnew=pointsがデータ数
# 周期カーネルでGP回帰
N = 15
points = np.linspace(0, 10, 100)[:, None] # 重回帰用 shape [100, 1]
x = np.random.uniform(0, 10, size=N)
x = x[np.argsort(x)][:, None] # shape [N, 1]
y = np.random.normal(np.sin(x), scale=0.2)[:, 0] # 目的変数 shape [N]
print(x.shape, y.shape, points.shape)
with pm.Model() as model:
# prior
ls = pm.Gamma("ls", alpha=2, beta=0.5)
eta = pm.Gamma("eta", alpha=3, beta=1)
sigma = pm.HalfCauchy("sigma", beta=5)
# gaussian process
mean = pm.gp.mean.Zero()
cov = eta**2 + pm.gp.cov.ExpQuad(input_dim=1, ls=ls, active_dims=[0]) # input_dimは特徴量の列数
gp = pm.gp.Marginal(mean_func=mean, cov_func=cov)
p_y = gp.marginal_likelihood("f", X=x, y=y, sigma=sigma)
trace = pm.sample(2000, chains=1, cores=1)
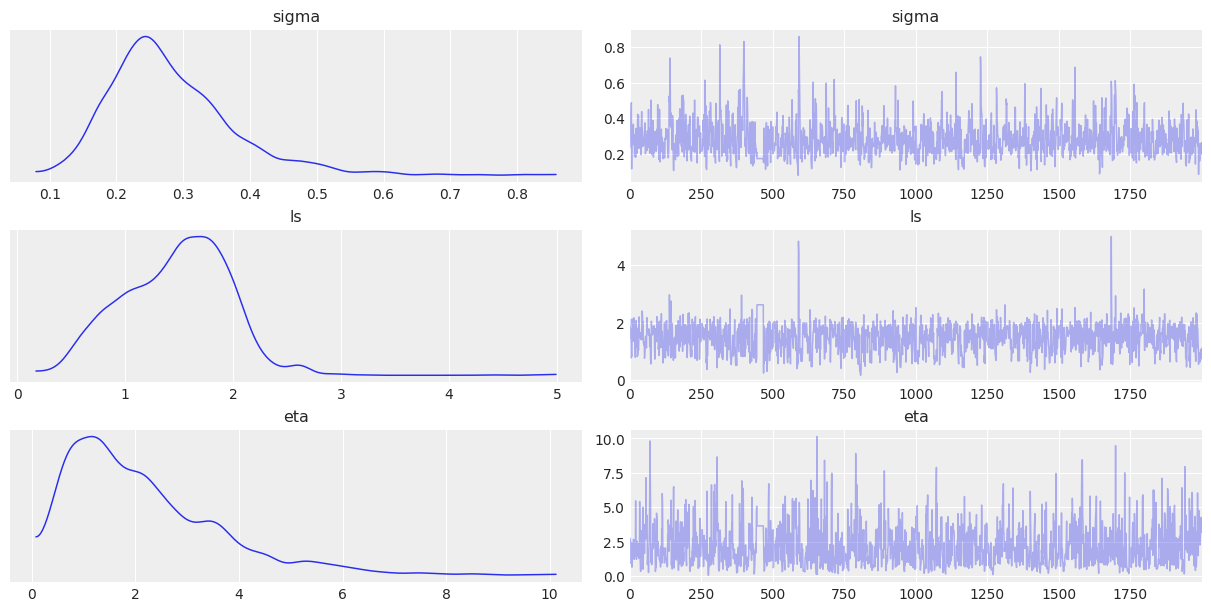
var_names = ["sigma", "ls", "eta"]
az.plot_trace(trace, var_names=var_names)
az.summary(trace, var_names=var_names)
plt.show()
with model:
preds = gp.conditional("y_pred", points)
samples = pm.sample_posterior_predictive(trace, var_names=["y_pred"])
非常に時間がかかる。
(15, 1) (15,) (100, 1)
f_pred = samples.posterior_predictive["y_pred"].mean(dim=["chain"]) # shape [draw: 2000, y_pred_dim_2: 100]
print(f_pred)
for f in f_pred:
plt.plot(points, f.values, color="r", alpha=0.01, zorder=1)
plt.scatter(x, y, color="b", zorder=2)
plt.ylim(-2, 2)
plt.show()
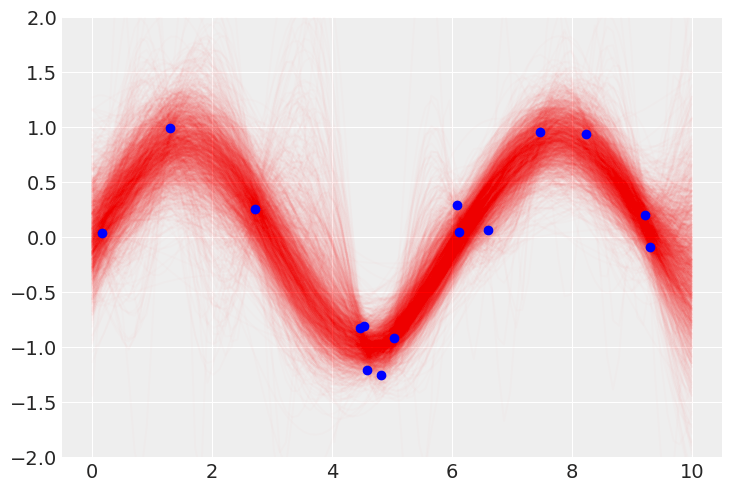
drawに関して平均を取れば最高事後予測の回帰関数が得られる。
実際にやってみた感じとしては、正直遅すぎて使い所がわからない感じがした。公式ドキュメントでも特徴量が2列251要素の単回帰に対してMCMCで50分近くかかっている例が挙げられており、「それならNNのほうが早いし柔軟なのでは...」となる。説明性に関しても正直そんなに高く感じない(まだ習熟していないからそう思うだけかも知れないが)ので、使い所がわからないような...
かなり苦戦したが、以上の方法でガウス過程を使って柔軟な曲線を補完する関数を推論でき、その関数空間の確率分布まで出せることが示せた。
感想
Pythonによるベイズ統計モデリング(PyMCでのデータ分析実践ガイド)を一通り読み、各所でPRMLの理論面を振り返ることで実際のデータ分析実装と背景を頭に入れることができた。
実際のオープンなデータでなにか例題があれば勉強がてら記事にしたいが、意思決定系のプロの人が書いた本とかがほしいものの調べる限りめぼしいものが見当たらない...
データ収集と分析、それによるアクションなど(理論というよりビジネス的な領域?)の名著や定番書でおすすめのものがあれば教えてください。
Discussion