ScoreCardシーリズ（2）——証拠の重さと情報価値(WOE and IV)

スコアカードモデリング入門シリーズ

1. スコアカードの由来
2. 証拠の重さと情報価値（WOE and IV）
3. グルーピングの方法（Grouping Method）
4. 信頼できるAIの要素——PSI（Population Stability Index）
5. スコアの計算
6. 実例：モデルの構築

ソースコード：GitHub Repository

証拠の重さ（WOE、Weight of Evidence）

WOEは"Weight of Evidence"（証拠の重さ）の略称であり、原始変数を符号化したものです。変数をWOEエンコードする際には、まず変数のグルーピング（Binning）が必要です。グルーピングには複数の手法がありますが、これらについては後述します。

i番目のグループのWOE計算式は以下の通りです：

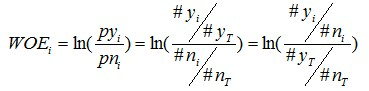
ここで：

• yi：当該グループのポジティブサンプル数
• ni：当該グループのネガティブサンプル数
• yT：全サンプル中のポジティブサンプル総数
• nT：全サンプル中のネガティブサンプル総数
• ポジティブ：二項分類における1のケース
• ネガティブ：二項分類における0のケース

この計算式によるWOEは以下のように解釈できます：

• グループ内のポジティブ・ネガティブ比率（A）が全体の比率（B）より大きい場合、WOEは正の値となります
• グループ内の比率が全体の比率より小さい場合、WOEは負の値となります

情報価値（IV、Information Value）

IVの用途

IVは特徴量の予測能力を数値化した指標です。機械学習モデルの構築時には多数の特徴量が存在し、それらの重要度を客観的に評価する必要があります。IVはそのための定量的指標の一つで、値が大きいほど予測能力が高いことを示します。

IVの計算

WOEを用いて、i番目のグループのIVは以下のように計算されます：

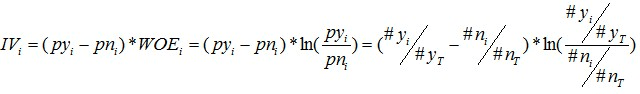
特徴量全体のIVは、各グループのIVの総和として計算されます：

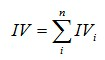
実例による解説

あるマーケティングキャンペーンの事例を用いて説明します。顧客の反応を予測するため、10万件の過去データを分析します。以下の特徴量が利用可能です：

• 過去1ヶ月の購買有無
• 直近購入額
• 直近購入商品カテゴリ
• VIP会員フラグ

これらの特徴量は既にグループ化されており、以下のような分布となっています：

(1)

直近一ヶ月買うことがあるか	応じる	応じない	合計	応じるパーセンテージ
はい	4000	16000	20000	20%
いいえ	6000	74000	80000	7.5%
合計	10000	90000	100000	10%

(2)

直近一回の購入金額	応じる	応じない	合計	応じるパーセンテージ
<100	2500	47500	50000	5%
[100,200)	3000	27000	30000	10%
[200,500)	3000	12000	15000	20%
>=500	1500	3500	5000	30%
合計	10000	90000	100000	10%

(3)

直近一回の購入商品のカテゴリ	応じる	応じない	合計	応じるパーセンテージ
電気	3000	57000	60000	5%
化粧品	2000	18000	20000	10%
食べ物	5000	15000	20000	25%
合計	10000	90000	100000	10%

(4)

VIP顧客か	応じる	応じない	合計	応じるパーセンテージ
はい	5500	4500	10000	55%
いいえ	4500	85000	90000	5%
合計	10000	90000	100000	10%

WOEとIVの計算例

直近購入額を例に計算プロセスを示します：

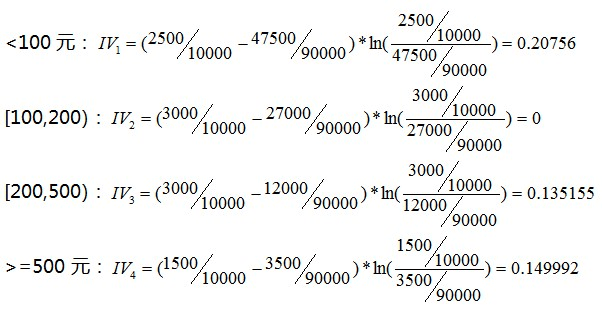
上記の計算結果をまとめて、このようになります。

直近一回の購入金額	応じる	応じない	合計	応じるパーセンテージ	WOE	IV
<100	2500	47500	50000	5%	-0.74721	0.20756
[100,200)	3000	27000	30000	10%	0	0
[200,500)	3000	12000	15000	20%	0.81093	0.135155
>=500	1500	3500	5000	30%	1.349927	0.149992
合計	10000	90000	100000	10%	0	0.492706

この計算結果から、以下が分かります：

1. 反応率が高いほどWOEも高くなる
2. グループの反応率が全体平均より低いとWOEは負、高いと正、同じなら0となる
3. WOEは実数全体の値を取り得る

注意事項：
IVは[0,+∞)の範囲を取ります。極端なケースでは無限大となる可能性があり、その場合はグループの再分割や擬似サンプルの追加などの対処が必要です。

特徴量の予測能力評価

各特徴量のIV値は以下の通りです：

• VIP会員フラグ: 1.56550367
• 直近購入商品カテゴリ: 0.615275563
• 直近購入額: 0.492706
• 過去1ヶ月購買有無: 0.250224725

予測能力の順位は以下となります：

1. VIP会員フラグ
2. 直近購入商品カテゴリ
3. 直近購入額
4. 過去1ヶ月購買有無

もしデータ特徴を選択したい場合、IVを通じて選択ができます。

IVの意義

IVをWOEより優れた予測力指標とする理由は以下の通りです：

1. 予測能力の指標として望ましい正の値のみを取ります
   

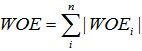
2. サンプル数の重みを適切に反映します。例えば：

A	応じる	応じない	合計	応じるパーセンテージ	WOE	IV
１	90	10	100	90%	4.39444	0.039062
0	9910	89990	99900	10%	-0.00893	7.937E-5
合計	10000	90000	100000	10%	4.40337	0.039141

上記の例では、WOEは高いもののサンプル数が少ないため、IVは低い値となっています。これは、実際の予測への寄与度を適切に反映した結果といえます。

IVは(Pyi - Pni)による重み付けを行うことで、単純なWOEの総和よりも予測力をより正確に表現できます。