金融与信モデル（3）——離散化（グルーピング）の方法(Grouping Method)

金融与信モデル入門シリーズ

1. スコアカードの由来
2. 証拠の重さと情報価値（WOE and IV）
3. グルーピングの方法（Grouping Method）
4. 信頼できるAIの要素——PSI（Population Stability Index）
5. スコアの計算
6. 実例：モデルの構築

ソースコード：GitHub Repository

データの離散化（グルーピング）

離散化（グルーピング）とは、連続的な量的データを区間ごとに分割し、質的データへと変換する手法です。

教師なし離散化

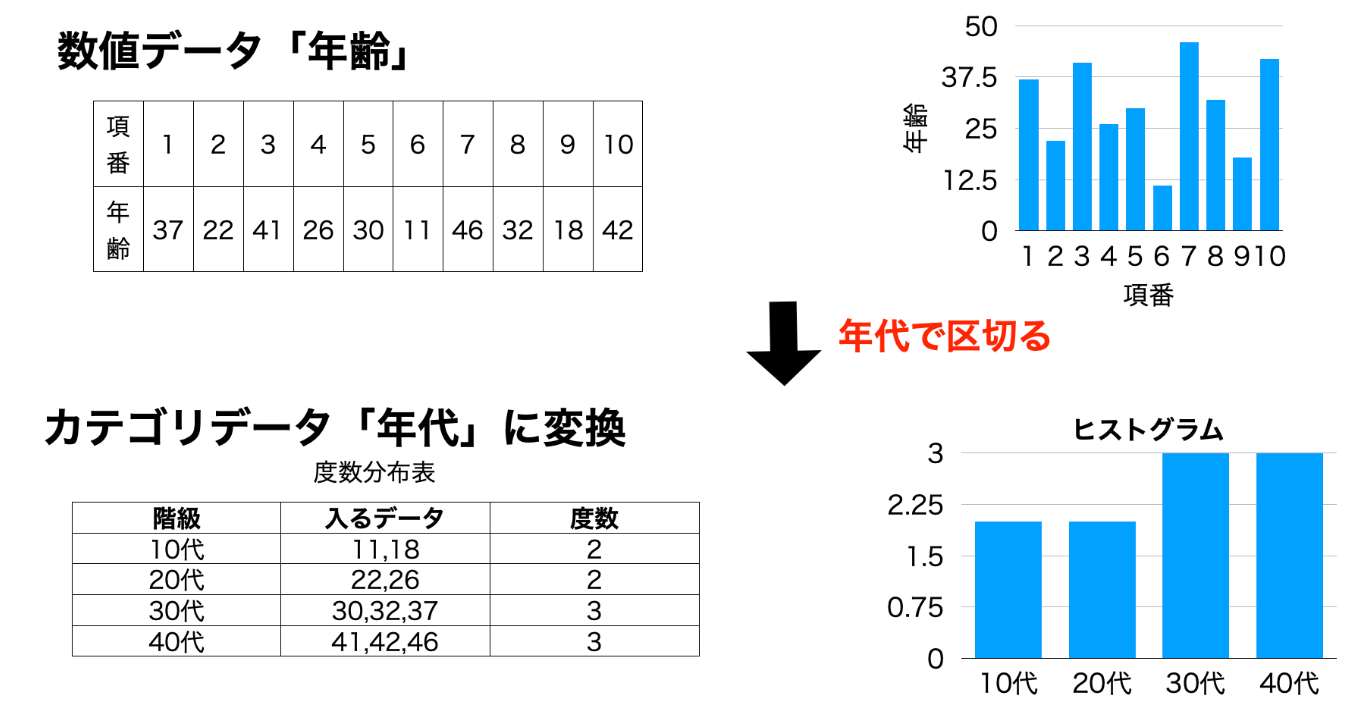
等間隔離散化

予め一定の区間幅を設定し、各データを該当する区間に振り分ける手法です。全ての区間が同じ幅を持つことが特徴です。

等頻度離散化

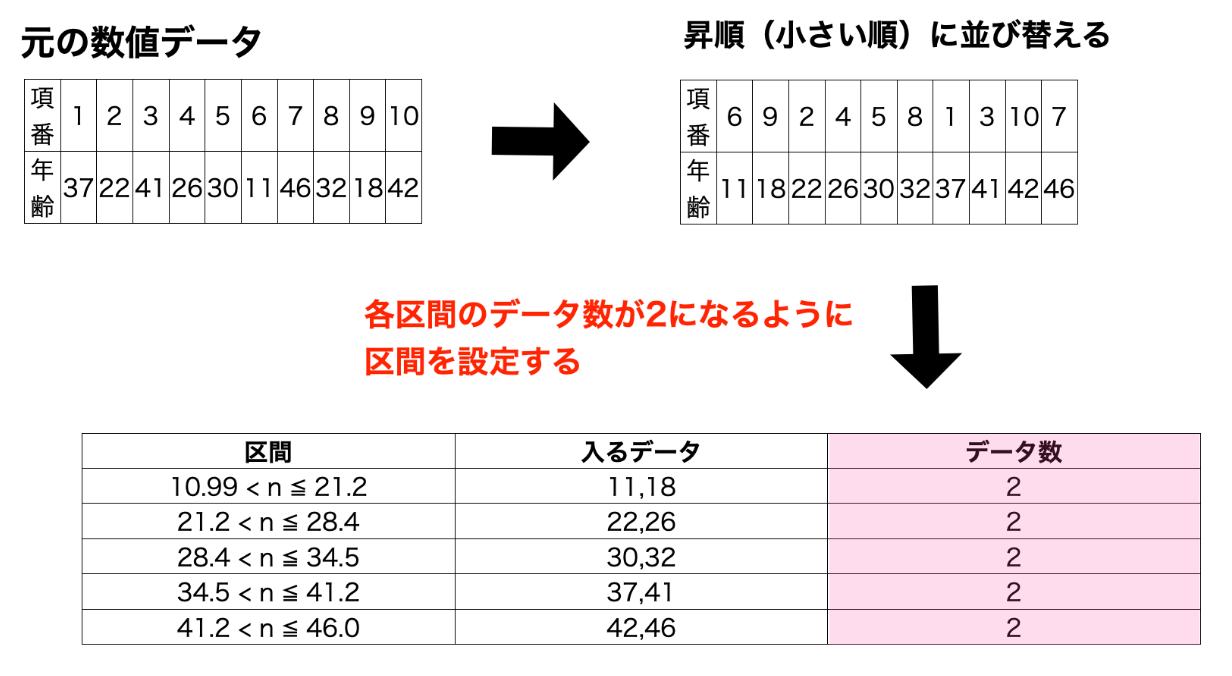
各区間に含まれるデータ数が等しくなるように区間を設定する手法です。データの分布に応じて区間幅は可変となります。

教師あり離散化

教師なし離散化が特徴量のみを考慮するのに対し、教師あり離散化は目的変数（Yラベル）との関係性を考慮して区間を決定します。

決定木による離散化

アプローチ：

1. 離散化対象の特徴量と目的変数を用いて簡単な決定木モデルを構築
2. 決定木の分割点に基づいて区間を設定
3. 各区間の指標を算出

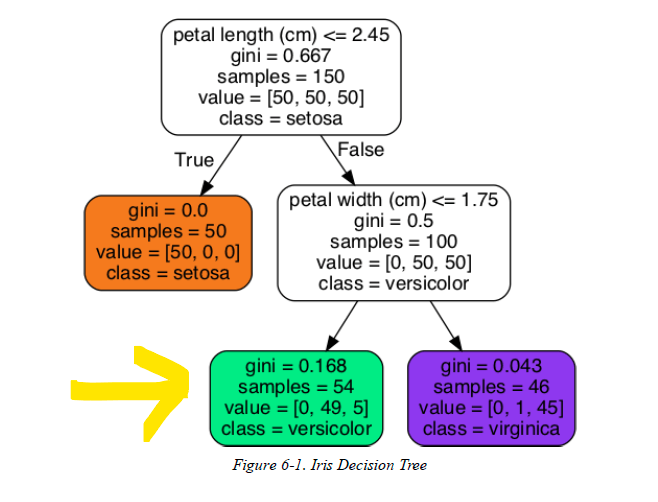
最終的な区分は以下のようになります：

単調性を考慮した離散化

決定木による分割では、区間ごとの目的変数の比率が必ずしも単調（単調増加または単調減少）とはなりません。単調性とは、値が一貫して増加または減少する性質を指します。

モデルの解釈性を高めるため、以下のような単調な関係性を持つ離散化が望ましい場合があります：

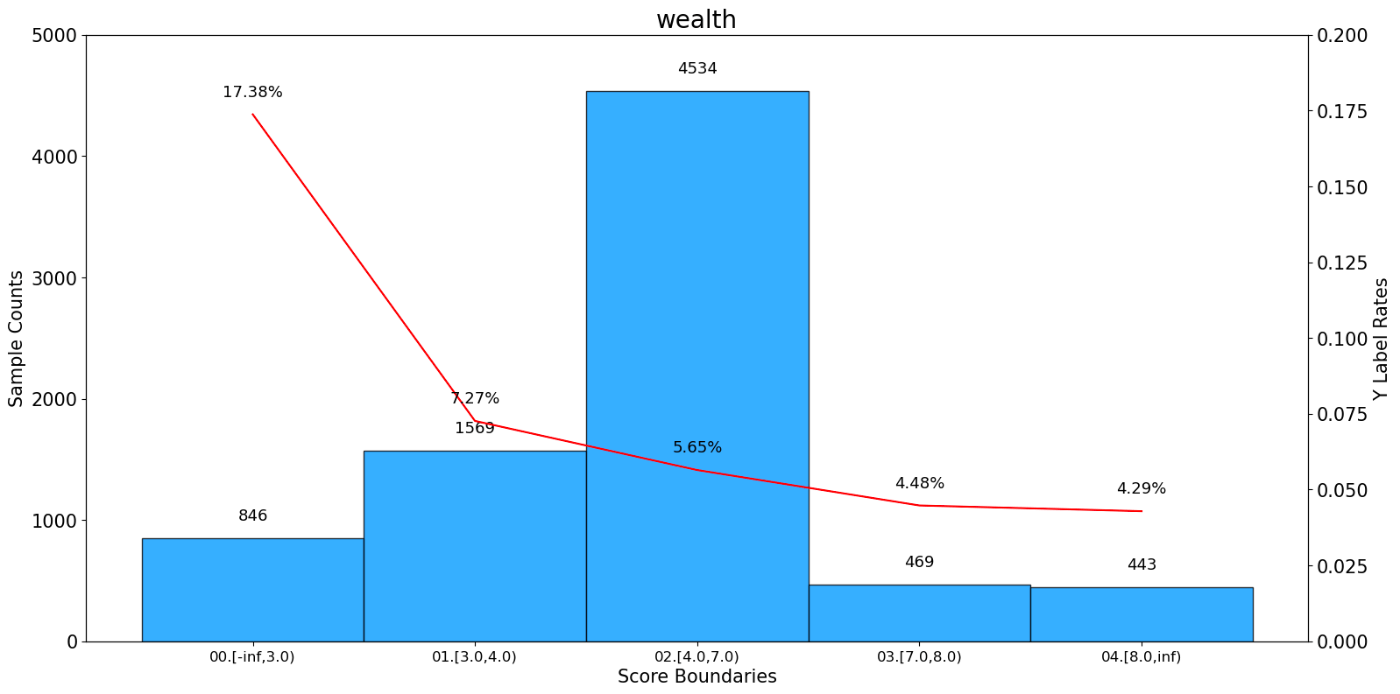
このような単調な関係性は、モデルの動作原理を説明する際により直感的な理解を促します。

---

データサイエンス君のAI教材シリーズ(未経験OK)
教材のターゲット層:

• 初心者: Pythonとデータ分析の基本を学びたい人
• 中級者: より高度な分析手法や機械学習を習得したい人
• レコメンド（推薦）エンジニア: レコメンデーションエンジンを作り、キャリアアップを目指したい人

AI領域に携わりたい方はぜひ！
datasciencekunのAI教材シリーズ

LINE公式アカウント
データサイエンス君のLINE公式アカウント友達募集中！
今登録すれば、下記の内容をプレゼントします！

• 特典資料：AI教材の一部を無料でお送りします！
• 専門家との相談：メッセージでデータサイエンス領域の不明点が相談できます！

一人で学ぶより、仲間と一緒に成長しませんか？
今すぐ友達登録して、データサイエンスの旅を始めましょう！
LINE公式アカウント：https://line.me/R/ti/p/@datasciencekun?from=page&accountId=datasciencekun