🐸

Rustで動的計画法：Frog 3

2023/09/29に公開

Rust

AtCoder

動的計画法

tech

はじめに

動的計画法を実装してみて、Rustの勉強をやってみる。問題としてはEducational DP Contestという動的計画法の練習を目的としたコンテストのものを使用。

https://atcoder.jp/contests/dp/

AからZまで問題が設定されており、今回は最後のZ Frog 3を解いてみる。結構有名な問題らしく解法の解説は多い。

利用したライブラリ

標準入力からデータを読み取る部分はproconioを利用。

chmaxのマクロも利用。

解き方

動的計画法

普通にやるとこうなるよね。という解き方。最初にあったFrog, Frog 2との違いは、カエルがジャンプする距離に制限がないこと。このため、内側のループも $n$ に依存するようになるので、 $O(n^2)$ になる。ちょっとの違いだけど計算量でいくと結構大きい。なので、内側のループをいかに小さくするかがポイントであるが、良い手がないので、このような問題を解くためのアルゴリズムに頼ることにする。

main_dp.rs

fn main() {
    input! {
        n : usize, c : u64,
        mut footholds : [u64; n]
    }

    let mut dp = vec![u64::MAX; n];
    dp[0] = 0; 
    for j in 1..n {
        for i in 0..j {
            chmin!(dp[j], dp[i] + (footholds[j] - footholds[i]).pow(2) + c);
        }
    }

    let answer = dp[n - 1];
    println!("{}", answer);
}

Convex Hull Trick (CHT)

複数の直線の集合から、各 $x$ における最小値を求めるためのアルゴリズム。何に使うかというと

\textrm{dp}[i] = \min_{0\leq j < i}\left\{ a_j x_i + b_j \right\} + c_i

のような形で表される問題を実装方法にもよるが、 $O(n\log n)$ で解く時に使う。さらに、処理として $i > j \Rightarrow a_i < a_j, x_i > x_j$ が満たされるなら $O(n)$ で解くことができ、実装も簡単。今回はこの条件を満たす。くわしい説明は検索するといろいろでてくるかとは思うが、このスライドがわかりやすかった。

今回の問題の場合は、

\textrm{dp}[i] = \min_{0\leq j < i}\left\{ (h_i - h_j)^2 + \textrm{dp}[j] + C\right\}

であるが、変形すると以下のようにCHTが使える形式に変換できる。

\textrm{dp}[i] = \min_{0\leq j < i}\left\{ (-2 h_j) h_i + (\textrm{dp}[j] + h_j^2) \right\} + (h_i^2 + C)

main_cht.rs

use proconio::input;
use num_traits::{Zero, NumOps};
use std::collections::VecDeque;

// LF : Liner Function
pub struct LF<T> {
    a: T,
    b: T
}

impl<T> LF<T>
where
    T: NumOps + Copy
{
    pub fn new(a:T, b:T) -> Self {
        Self {a, b}
    }

    pub fn calc(&self, x:T) -> T {
        self.a * x + self.b
    }
}


pub struct CHT<T> {
    line : VecDeque<LF<T>>,
    priv_a : T,
    priv_x : T,
}

impl<T> CHT<T>
where
    T: Zero + PartialOrd + NumOps + Copy
{
    pub fn new() -> Self {
        Self {
            line:   VecDeque::<LF<T>>::new(),
            priv_a: T::zero(),
            priv_x: T::zero()
        }
    }

    fn check(&self, f1_index:usize, f2_index:usize, f3:&LF<T>) -> bool {
        let f1 = self.line.get(f1_index).unwrap();
        let f2 = self.line.get(f2_index).unwrap();
        (f2.a - f1.a) * (f3.b - f2.b) >= (f2.b - f1.b) * (f3.a - f2.a)
    }

    pub fn add(&mut self, f:LF<T>) {
        assert!(self.line.len() < 1 || self.priv_a >= f.a);
        while self.line.len() >= 2 && self.check(self.line.len() - 2, self.line.len() - 1, &f) == true {
            self.line.pop_back();
        }
        self.priv_a = f.a;
        self.line.push_back(f);
    }

    pub fn get(&mut self, x:T) -> T {
        assert!(self.line.len() < 1 || self.priv_x <= x);

        while self.line.len() >= 2 && self.line.get(0).unwrap().calc(x) >= self.line.get(1).unwrap().calc(x) {
            self.line.pop_front();
        }
        self.priv_x = x;
        self.line.get(0).unwrap().calc(x)
    }
}

fn main() {
    input! {
        n : usize, c : i64,
        mut footholds : [i64; n]
    }

    let mut cht = CHT::<i64>::new();
    let mut dp = vec![0; n];
    for i in 1..n {
        cht.add(LF::new(-2 * footholds[i-1], dp[i-1] + footholds[i-1].pow(2)));
        dp[i] = cht.get(footholds[i]) + footholds[i].pow(2) + c;
    }

    let answer = dp[n - 1];
    println!("{}", answer);
}

LARCH

この問題のユーザ解説記事にあったアルゴリズム。遷移コスト $W(i,j)$ が以下の式を満たすとき、

i < i' < j < j' \Longrightarrow W(i,j) + W(i', j) \leq W(i,j') + W(i', j)

以下の問題を $O(n)$ で解くというもの。

dp[i] = dp[j] + W(i, j)

汎用性が高そうなアルゴリズムに感じる。良い解説はちょっと見つからなかったが、Rustでの実装も解説記事にあったのでベンチマークとしてそれをつかう。

測定結果

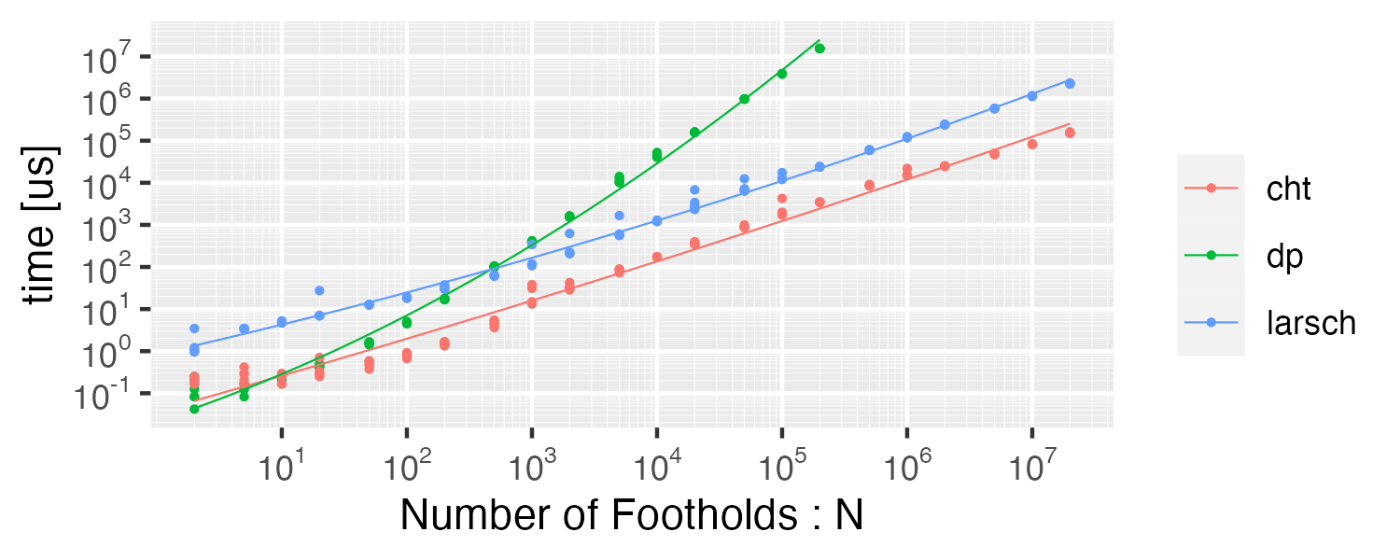
測定結果は以下のようになる。素直な実装では $O(n^2)$ なので、 $n$ が大きくなると計算量が大きくなってしまう。LARCHは汎用性の高い実装であったが、CHTは今回の問題に特化してシンプルな実装方式でよかったので速くなっている。

ここらへんになるとアルゴリズムを知っているか知らないかという問題になってくると思う。

過去の記事

はじめに

利用したライブラリ

解き方

動的計画法

Convex Hull Trick (CHT)

LARCH

測定結果

過去の記事

Discussion