⏱️

Rustで動的計画法：Intervals

2023/09/13に公開

Rust

AtCoder

動的計画法

tech

はじめに

動的計画法を実装してみて、Rustの勉強をやってみる。問題としてはEducational DP Contestという動的計画法の練習を目的としたコンテストのものを使用。

https://atcoder.jp/contests/dp/

AからZまで問題が設定されているが、今回はWのIntervalsを解いてみる。区間ごとに点数が決められていて、最高得点を取得するための組み合わせを求める問題。点数が正の数だけであれば、オール1が答えになるが、負の数が入るのでそれを考慮する必要がある。

利用したライブラリ

標準入力からデータを読み取る部分はproconioを利用。

ベクタから重複を削除するためにitertoolsに入っているdedupを使う。

完成したコード

アルゴリズム

$r_i \leq k$ を満たす区間 $(l_i, r_i, a_i)$ だけを使うことを考える。この時、一番右に位置する1が $j (j \leq k)$ ビット目である時の最大値をdp[k][j]とする。この時、dp[k-1][j]からどうやってdp[k][j]を求めるかであるが、簡単化のために、 $(l_i, k, a_i)$ となる区間が1つだけある例でいくと、以下のようになる。

dp[k][j] = \begin{cases} dp[k-1][j] & \textrm{where } j < l_i,\\ dp[k-1][j] + a_i & \textrm{where } l_i \leq j < k,\\ \max(dp[k-1][\cdot]) + a_i & \textrm{where } j = k . \end{cases}

kビット目が1の時は、k-1の最大値に $a_i$ を追加したもの。kビット目が0の時でも、新たに追加した区間内に1がある場合は、 $a_i$ を追加しないといけないという事になる。もし、 $(l_i, k, a_i)$ となる区間が複数あった場合においても $a_i$ を区間ごとに加えていけば良い。 $(l_i, k, a_i)$ となる区間がない場合は $a_i$ がないので、 $j=k$ の位置に最大値をいれてしまえば終わり。

$(l_i, k, a_i)$ となる区間が複数あった場合においても、 $a_i$ を区間ごとに加えていけば良い。

ベース実装

main_base.rs

use proconio::input;

fn main() {
    input! {
        n : usize, m : usize,
        mut ranges : [(usize, usize, i64); m]
    }

    ranges.sort_by(|(_, r1, _), (_, r2, _)| r1.cmp(r2));
    let mut dp = vec![0_i64; n + 1];
    let mut right_index = 0;
    for (l, r, a) in ranges {
        if right_index < r {
            let max_value = dp[0..=right_index].iter().max().unwrap().clone();
            for i in (right_index + 1)..=r {
                dp[i] = max_value;
            }
        }
        right_index = r;

        for i in l..=r {
            dp[i] += a;
        }
    }
    let max_value = dp.iter().max().unwrap().clone();
    println!("{}", max_value);
}

前述のアルゴリズムを素直に実装すると上記のようになる。dpは上書きする形で、 $dp[j]$ のみを考える。 $dp[0]$ は1が存在しない場合を表す。また、 $r_i = k$ のある区間があるかどうかが大事なので、ループは区間rangesで回す。この数が $M$ なので、 $O(M)$ と思いきや、最大値をmax()で求める時のコストやfor i in l..=rのループが $N$ に依存するので、 $O(MN)$ となる。

まず、 $r_i$ でソートして、その順番に処理していく。前回の区間の $r_{i-1}$ と $r_i$ の間は、 $(l_i, k, a_i)$ となる区間が存在しなかった場合なので、最大値を代入している。 $j=k$ の時も最大値を入れているので、区間内に報酬を足していけば処理は終わる。

main_base.rs

for i in (right_index + 1)..=r {
	dp[i] = max_value;
}

個人的に、終点を含むrangeを表す時の=rの記法は分かりやすくで好き。

座標圧縮

main_compress.rs

use proconio::input;
use itertools::*;
use std::collections::HashMap;

fn main() {
    input! {
        n : usize, m : usize,
        mut ranges : [(usize, usize, i64); m]
    }

    ranges.sort_by(|(_, r1, _), (_, r2, _)| r1.cmp(r2));
    
+   let mut values = Vec::with_capacity(m * 2 + 1);
+   values.push(0_usize);
+   for (l, r, _) in &ranges {
+       values.push(*l);
+       values.push(*r);
+   }
+   values.sort();
+   let compressed = values.into_iter().dedup().enumerate().map(|(enu, index)| (index, enu)).collect::<HashMap<_,_>>();

    let mut dp = vec![0_i64; n + 1];
    let mut right_index = 0;
    for (l, r, a) in ranges {
+       let cl =  compressed.get(&l).unwrap();
+       let cr =  compressed.get(&r).unwrap();
        
+       if right_index < *cr {
            let max_value = dp[0..=right_index].iter().max().unwrap().clone();
+           for i in (right_index + 1)..=*cr {
                dp[i] = max_value;
            }
        }
+       right_index = *cr;

+       for i in *cl..=*cr {
            dp[i] += a;
        }
    }
    let max_value = dp.iter().max().unwrap().clone();
    println!("{}", max_value);
}

$(l_i, k, a_i)$ となる区間が存在しない時、 $dp[k]$ には最大値を挿入して、以降も区間に入った場合に処理がなされる。ここが無駄なので座標圧縮を考える。
つまり以下の2つの問題は答えは同じだけど、dpの長さは100と3になる。なので、不要な部分を削除してしまう。

100 2
1 100 10
1 50 -10

3 2
1 3 10
1 2 -10

main_compress.rs

values.sort();
let compressed = values.into_iter()
	.dedup()
	.enumerate()
	.map(|(enu, index)| (index, enu))
	.collect::<HashMap<_,_>>();

必要なのは、 $l_i, r_i$ に含まれる場所だけなので、 $l_i, r_i$ を集めて、ソートして、連続する重複を削除して(dedup)、番号をつけて(enumerate)、順番を入れ替えて(map)、ハッシュにする(collect). dedupの実装は中々面白いので興味があれば検索すると良いと思う。

collectでHashMapを作る時に上記の記述の方がハッシュ化している感があって好みではあるが、検索してみると以下の記述の方が多い気がした。変数の型が明確になるという理由からかも知れない。

collect

let compressed: HashMap<_,_> = ...collect();

セグメント木

main_segment.rs

use proconio::input;
use std::collections::HashMap;
use itertools::*;

mod lazy_segment_tree;

fn main() {
    input! {
+       _ : usize, m : usize,
        mut ranges : [(usize, usize, i64); m]
    }

    ranges.sort_by(|(_, r1, _), (_, r2, _)| r1.cmp(r2));
    let mut values = Vec::with_capacity(m * 2 + 1);
    values.push(0_usize);
    for (l, r, _) in &ranges {
        values.push(*l);
        values.push(*r);
    }
    values.sort();
    let compressed = values.into_iter().dedup().enumerate().map(|(enu, index)| (index, enu)).collect::<HashMap<_,_>>();

    let n = compressed.len() - 1;
+   let mut dp = lazy_segment_tree::LazySegmentTree::new(
+       n + 1,
+       0,
+       |x, y| std::cmp::max(x, y),
+       || i64::MIN,
+       |l, v| match l { Some(value) => value + v, None => v },
+       |f, g| match (f, g) { (Some(fv), Some(gv)) => Some(fv + gv), (Some(_), None) => f, (None, _) => g });

    let mut right_index = 1;
    for (l, r, a) in ranges {
        let cl =  compressed.get(&l).unwrap();
        let cr =  compressed.get(&r).unwrap();
        if right_index < *cr {
+           let max_value = dp.prod(0..=right_index);
+           dp.apply(Some(max_value), (right_index + 1)..=*cr);
        }
        right_index = *cr;
+       dp.apply(Some(a), *cl..=*cr);
    }
+   let max_value = dp.prod(0..=n);
    println!("{}", max_value);
}

この問題の場合、区間に対する操作が多いので遅延評価セグメント木を使ってみる。以前Flowers で使ったFenwick Tree (BIT) が0から始まる区間の操作を対象にしていたが、こちらは任意の区間にしたもの。遅延評価セグメント木は各操作を $O(\log n)$ 時間に短縮できるので、このコードの計算量は $O(M\log{N})$ となる。

遅延評価セグメント木と、普通のセグメント木とあるが、今回のように区間の値を一度に更新したい場合は遅延評価が必要。調べているとすでに実装があった。

測定結果

gen_interval.py

#!/user/bin/env python
import random
import sys

n = int(sys.argv[1])
m = int(sys.argv[2])

RANGE = 1000
random.seed()

print(str(n) + " " + str(m))
for i in range(m):
    l = random.randrange(1, n + 1)
    r = random.randrange(0, min(RANGE, n - l + 1)) + l
    a = random.randrange(-1000000000, 1000000000)
    print(str(l) + " " + str(r) + " " + str(a))

スクリプトで自動的に問題を作成して評価をしてみた。区間の長さは1000未満としているので、for i in l..=rのループは $N$ に依存しない。

Nに対する計算量

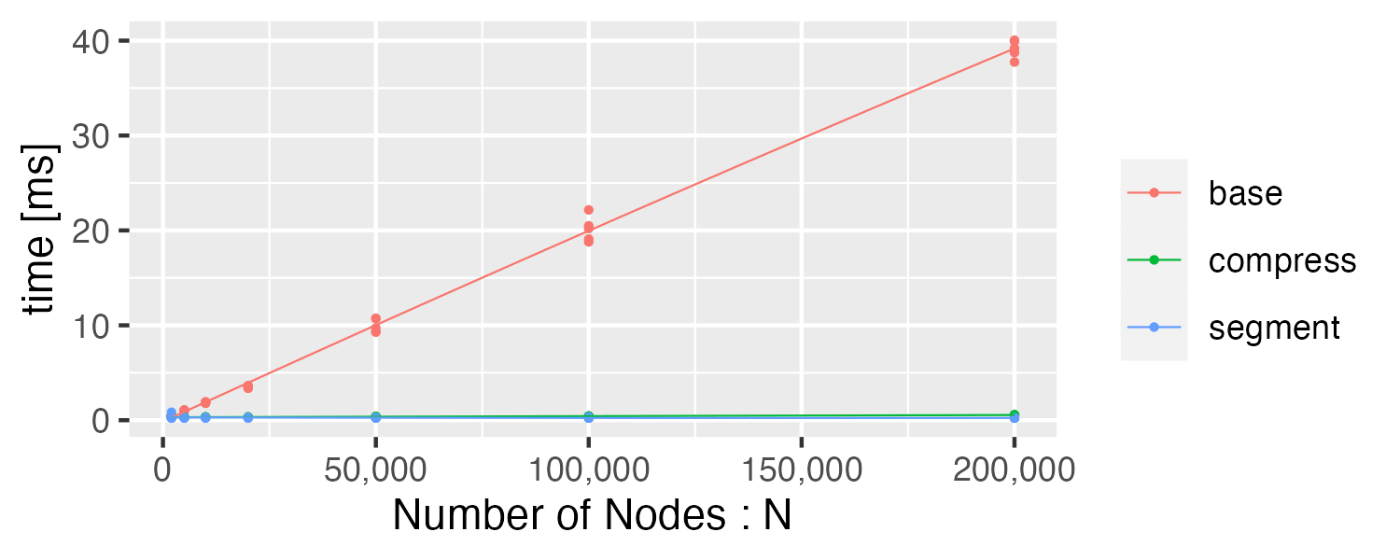
$M$ を500に固定して $N$ を変化させた時のグラフ。minのコストが意外とかかっているのが分かる。座標圧縮をすると、dpの長さが $M$ に依存するようになるので、オーダー的には $O(M^2)$ となり $N$ を変化させた時のグラフでは傾きが無くなる。

Mに対する計算量

$N$ を $2.0\times 10^5$ に固定して $M$ を変化させた時のグラフ。 $M$ が大きくなると座標圧縮の効果は低くなるので差は小さくなるが、それでも高速化ができている。セグメント木はオーダーが違うので速い。