🌿

Rustで動的計画法：Subtree

2023/08/11に公開

Rust

AtCoder

動的計画法

tech

はじめに

動的計画法を実装してみて、Rustの勉強をやってみる。問題としてはEducational DP Contestという動的計画法の練習を目的としたコンテストのものを使用。

https://atcoder.jp/contests/dp/

AからZまで問題が設定されているが、今回はVのSubtreeを解いてみる。rootが同じ部分木を求める問題。すべてのノードをrootとした時の答えをださないといけないので、計算量が増える可能性があるのが課題である。

利用したライブラリ

標準入力からデータを読み取る部分はproconioを利用。

ベクタから条件にあう要素の位置を得るためにitertoolsに入っているpositionsを使う。

完成したコード

長いので、フルサイズはgistに置いている。

アルゴリズム

「黒い頂点のみを辿って到達できる」組み合わせの数と部分木の数は等しいので部分木を求める問題である。ここで、 $i$ を親とする時、ノード $j$ を根とする部分木の数 $f(i,j)$ は、ノード $j$ の隣接ノードの集合を $C_j$ とすると、以下の式で求められる。

f(i,j) = \prod_{k \in C_j - i} (1 + f(j, k))

言い方を変えると、 $i$ と $j$ が黒色の時に、 $j$ より先のノードの配色パターンの数が $f(i,j)$ となる。 $+1$ は、 $k$ が白色のパターンもあるため。

この時、 $i$ を根とした部分木の数、つまり $i$ が黒色の時の配色パターンの数は次式で求められる。

\prod_{k \in C_i} (1 + f(i, k))

つまり、すべての $f(i,j)$ を先に求め、その後に各ノードを根とした時の部分木の数を計算すれば良い。求め方としては、Indipendent Setで行なったように、リーフノードから上に計算していき、その後ルートノードから下に計算していく2段階で実施すれば良い。

下から上へ

subtree.rs

let mut queue: Vec<_> = nodes.iter()
    .positions(|node| node.neighbors.len() <= 1)
    .collect();

let root = 'bottom_up_loop: loop {
    let mut next_queue = Vec::new();
    for &i in queue.iter() {
        if let Some(parent) = nodes[i].set_parent_node() {
            let value = nodes[i].get_value(parent);
            if nodes[parent].set_child_value(i, value) == 1 {
                next_queue.push(parent);
            }
        } else {
            break 'bottom_up_loop i;
        }
    }
    queue = next_queue;
    assert!(queue.len() > 0);
};

リーフノードからルートノードに向かって計算する方法は、Indipendent Setと同じような形。まず、隣接ノードが1つしかないリーフノードをqueueに入れてループをスタートさせる。

$f(i, j)$ を計算できればnodes[i].set_child_value(j, value)で保存して進んでいく。その時nodes[i]の隣接ノードからjを削除する。 $f(p, i)$ が計算可能となるのは、iの隣接ノードのうち、p以外の $f(i,j)$ が計算できた時なので、残った隣接ノード数が1になった時に、計算可能としてnext_queueに挿入される。

最後にはルートノードの番号を返してrootに代入している。

上から下へ

subtree.rs

let mut queue = vec![root];
'top_down_loop: loop {
    let mut next_queue = Vec::new();
    for &i in &queue {
        for parent in nodes[i].value.clone() {
            let p = parent.0;
            if nodes[p].neighbors.len() > 0 {
                next_queue.push(p);
            }
            let value = nodes[i].get_value(p);
            let j = nodes[p].set_child_value(i, value);
            assert!(j == 0);
        }
    }
    if next_queue.len() == 0 {
        break 'top_down_loop;
    }
    queue = next_queue;
};

上から下の流れとしては、 $f(i,j)$ が全ての隣接ノード $j \in C_i$ に対して計算されていれば、 $f(j, i)$ は上記式から導出できることを利用する。まず、ルートノードに対しては成り立つので、まずルーフノードのみをqueueに入れ、隣接ノードに対して $f()$ を導出。隣接ノードは全ての $f()$ が導出されていることになるので、繰り返し実行すれば、完了する。

Immutable borrow

ちょっと無駄のように感じるのがここのclone()。

subtree.rs

        for parent in nodes[i].value.clone() {

普通にiter()にすると以下の場所でエラーがでる。

subtree.rs

            let j = nodes[p].set_child_value(i, value);

つまり、forでimmutable borrowしているnodesがset_child_value()の部分でmutable borrowになっているということ。書換不可で使っているものが途中で書き換えられちゃう（可能性がある）ためのエラーをだしている。実際はi != pなので、そんな事は起きないが、その条件をコンパイラに渡す方法は見当たらなかった。clone()してしまえばforのイテレータとnodesは分離されるので、エラーはでなくなる。

測定結果

Indipendent Setで使ったツリー生成のスクリプトを使って、ノード数と時間の関係を計測したのが以下のグラフ。

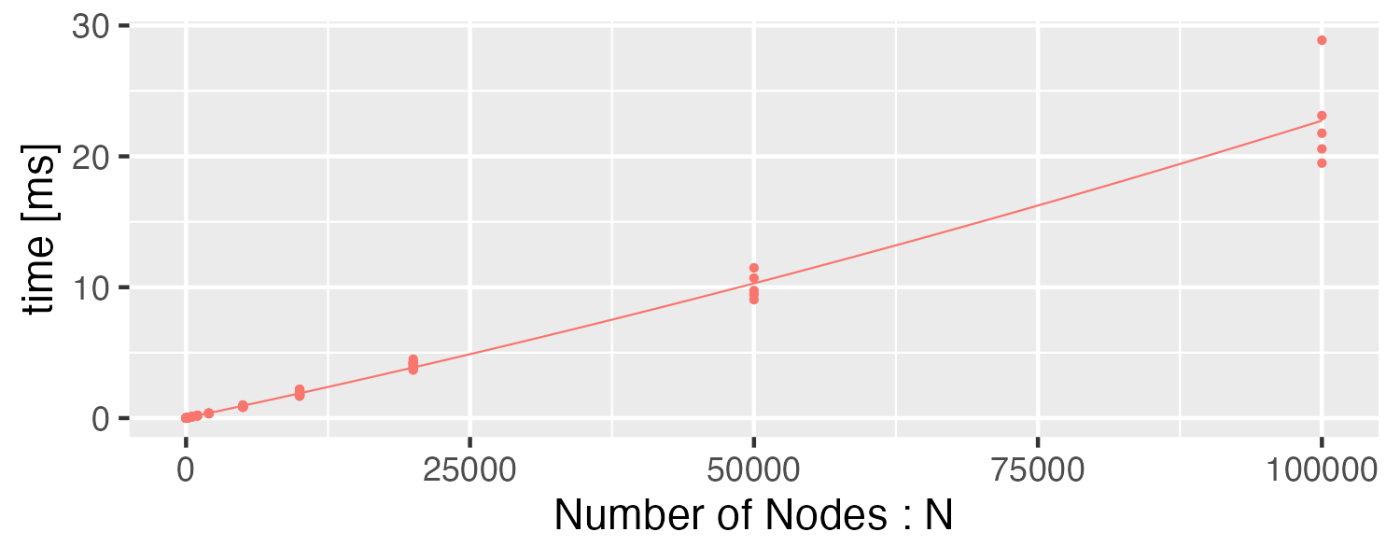
乗算の計算部分で、同じ計算を何度もやっている部分があるので何とかした方がいいのかな？とも思ったが、これで十分な結果がでた。（余計なことをした方が遅かった...）

Rustで動的計画法：Subtree

はじめに

利用したライブラリ

完成したコード

アルゴリズム

下から上へ

上から下へ

Immutable borrow

測定結果

関連記事

Discussion