👣

Rustで動的計画法：Walk

2023/05/16に公開

Rust

AtCoder

動的計画法

tech

はじめに

動的計画法を実装してみて、Rustの勉強をやってみる。問題としてはEducational DP Contestという動的計画法の練習を目的としたコンテストのものを使用。

https://atcoder.jp/contests/dp/

AからZまで問題が設定されているが、今回はRのWalkを解いてみる。有向グラフにおいて長さ $K$ のパスを数える問題。

利用したライブラリ

標準入力からデータを読み取る部分はproconioを利用。

行列演算を使うので、nalgebraを利用。競技プログラミングでは使えないのかも知れないが、あくまでRustの勉強のためなので。行列演算用のライブラリは他にもndarrayなどがあるらしい。
https://nalgebra.org

探索を使った解放

素直に幅優先探索として解いてみた。歩行者(walker)が1つずつノードを移動していって、その経路数を集計するイメージで実装。dp[i]を、今ノードiにwalkerがいた時、これまでの経路の数がdp[i]個となるとする。この時、dp[i+1]はdp[i]から隣接ノードテーブルを見てから移動する。

walk_breadth.rs

use proconio::input;

const MOD: u64 = 10u64.pow(9) + 7;

fn main(){
    input! {
        n: usize, k: usize,
        a: [[u64; n]; n]
    }

    let mut dp = vec![1u64; n];
    for _ in 0..k {
        let mut next_dp = vec![0u64; n];
        for i in 0..n {
            for j in 0..n {
                next_dp[j] = (next_dp[j] + a[i][j] * dp[i]) % MOD;
            }
        }
        dp = next_dp;
    }

    let ans: u64 = dp.iter().sum();
    println!("{}", ans);
}

計算量

計算量としては $O(KN^2)$ で、そんなに悪くないような気はするが、この問題の場合 $1 \leq K \leq 10^{18}$ と $K$ が大きいのが問題。上のコードではループ1回が $8\mu$ s程度だったので、 $K = 10^{18}$ の時は $8\times 10^{12}$ 秒つまり25000年かかってしまう。

行列演算として解く

ソースを見てわかるように、dpの更新は以下の行列演算を行なっているのに等しい。

\textit{dp}_{i+1} = \begin{pmatrix} a_{1,1} & a_{2,1} & \cdots & a_{n,1} \\ a_{1,2} & a_{2,2} & \cdots & a_{n,2} \\ \vdots & & \ddots & \vdots \\ a_{1,n} & a_{2,n} & \cdots & a_{n,n} \end{pmatrix}\begin{pmatrix} \textit{dp}_1 \\ \textit{dp}_2 \\ \vdots \\ \textit{dp}_n \end{pmatrix}

これを $k$ 回繰り返すので、求める値は以下の行列演算をして全ての要素を和を求めればいい。

\begin{pmatrix} a_{1,1} & a_{2,1} & \cdots & a_{n,1} \\ a_{1,2} & a_{2,2} & \cdots & a_{n,2} \\ \vdots & & \ddots & \vdots \\ a_{1,n} & a_{2,n} & \cdots & a_{n,n} \end{pmatrix}^k \begin{pmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{pmatrix}

nalgebraを用いた実装

素直な実装

行列演算ライブラリであるnalgebraを使って実装すると以下のようになる。
$K$ が小さい場合には問題なく動くが、 $K$ が大きくなるとpowでoverflowしてしまう。

walk_matrix.rs

use proconio::input;
use nalgebra as na;

const MOD: u64 = 10u64.pow(9) + 7;

fn main(){
    input! {
        n: usize, k: u64,
        a: [u64; n * n],
    }
    let path = na::DMatrix::from_iterator(n, n, a.iter().cloned());
    let one = na::DMatrix::repeat(n, 1, 1u64);
    let ans = (path.pow(length as u32) * one).sum() % MOD;
    println!("{}", ans);
}

オーバーフローしない実装

オーバーフローしないようにするにはpowを実装する必要がある。大きな階乗を求めるには二乗を計算していってその和で求める定番の方法を使った。オーダーとしては $O(\log K)$ になる。「これは動的計画法なのか？」と言われると良くわからないが。

最後に全ての要素が1の列ベクトルをかけるところと要素の和を求めるところは、まとめてmの要素の和を求めれば良いので、foldで処理した。

なお、 $K = 10^{18}$ の問題を解いてみると、10msで完了した。25000年は10msになるのだからアルゴリズムは大事。

walk_matrix_loop.rs

use proconio::input;
use nalgebra as na;

const MOD: u64 = 10u64.pow(9) + 7;

fn main(){
    input! {
        n: usize, k: u64,
        a: [u64; n * n],
    }
    let mut c = na::DMatrix::from_iterator(n, n, a.iter().cloned());
    let mut m = na::DMatrix::<u64>::identity(n, n);
    let mut length = k;
    
    loop {
        if length & 1u64 == 1u64 {
            m = (m.clone() * c.clone()).map(|x| x % MOD);
        }

        length >>= 1;
        if length == 0 {
            break;
        } else {
            c = c.pow(2u32).map(|x| x % MOD);
        }
    }
    let ans = m.fold(0u64, |s, v| (s + v) % MOD);
    println!("{}", ans);
}

計算処理時間の検証

データ作成

試験データに関しては、 $K$ がどんなに大きくても答えが0にならないように、すべてのノードを通過するループを1つ作って、後は適当に1割程度リンクをはるようにした。

gen_walk.py

#!/user/bin/env python
import random
import sys

n = int(sys.argv[1])
k = int(sys.argv[2])

neighbor = [[0 for i in range(n)] for j in range(n)]
loop = list(range(0, n))
random.shuffle(loop)

for i in range(n - 1):
    neighbor[loop[i]][loop[i + 1]] = 1
neighbor[loop[n - 1]][loop[0]] = 1

for i in range(int(n * n / 10)):
    neighbor[random.randrange(0, n)][random.randrange(0, n)] = 1

print(str(n) + " " + str(k))
for i in range(n):
    print(*neighbor[i])

計測結果

$N = 50$ にして、すべての方式で計算が終わる範囲で $K$ を変化させて計測した。解析通り $O(K)$ と $O(\log K)$ のグラフがプロットできた。自前で作成した行列の階乗計算も、ライブラリのものと同じような傾向なので、悪くない感じはする。

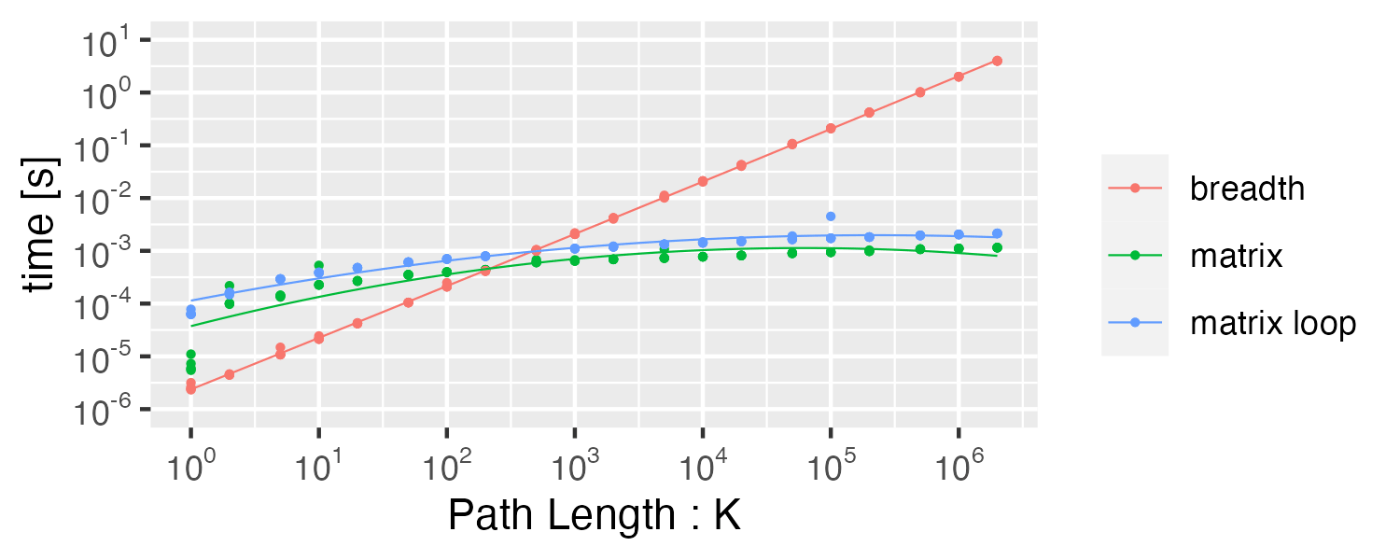
ライブラリのオーバーヘッドのためか、 $K < 100$ では探索の方が早いが、 $K$ が大きくなると行列演算を使った方が速いことがわかる。

numpyとの比較

素朴な疑問として「Rustって速いのか?」があるかと思う。そこでnumpyとの比較も行ってみた。ソースコードとしてはほぼ同じである。

walk.py

#!/user/bin/env python
import numpy as np

MOD = 10 ** 9 + 7

N, K = map(int, input().split())
A = [list(map(int, input().split())) for _ in range(N)]

c = np.array(A, dtype = np.uint64)
m = np.identity(N, dtype = np.uint64)
length = K

while True:
    if length & 1 == 1:
        m = np.dot(m, c) % MOD
    
    length >>= 1
    if length == 0:
        break
    else:
        c = np.dot(c, c) % MOD

ans = m.sum() % MOD
print(ans)

結果としては、ほぼ同等で最速値だとnumpyの方が速いが、ばらつきが大きいので平均するとnalgebraの方が速い。numpyもコストが高い演算部分は外部ライブラリを呼び出す形なので、差はでないというか、十分速い。