🗼

Rustで動的計画法：Tower

2023/09/22に公開

Rust

AtCoder

動的計画法

tech

はじめに

動的計画法を実装してみて、Rustの勉強をやってみる。問題としてはEducational DP Contestという動的計画法の練習を目的としたコンテストのものを使用。

https://atcoder.jp/contests/dp/

AからZまで問題が設定されているが、今回はXのTowerを解いてみる。丈夫さ $s$ を重さ $v$ が超えないようにブロックを積み上げていく問題。

利用したライブラリ

標準入力からデータを読み取る部分はproconioを利用。

chmaxのマクロも利用。

解き方

総当たり

ブロックを「積んでいく」問題なのだけど、積む方向で考えると、新しいブロックを積むたびに既存のブロックの「丈夫さ」が、新しく積んだブロックの重さを足しても耐えれるかの確認を行う必要がある。既に「積んだ」ものを意識しないようにしたいので、「積む」のではなく「下に新しいブロックを追加する」方向で考える。こうすると「既に積んであるブロックの重さ」が「新しく追加するブロックの丈夫さ」以下かどうかのチェックで済む。

そこで総当たりで求めると以下のようになる。計算量は $O(n!)$ なのでアルゴリズムとしてはダメ。でも入力例にあるような小さい問題であれば答えはでる。

main_brute_force.rs

use proconio::input;

fn stack_block(remaining_blocks:&Vec<(usize, usize, i64)>, stacked_weight:usize, stacked_value:i64) -> i64 {
    let mut value = stacked_value;
    for i in 0..remaining_blocks.len() {
        let (w, s, v) = remaining_blocks[i];
        if s >= stacked_weight {
            let mut blocks = remaining_blocks.clone();
            blocks.remove_swap(i);
            chmax!(value, stack_block(&blocks, stacked_weight + w, stacked_value + v));
        }
    }
    value
}

fn main() {
    input! {
        n : usize, 
        mut blocks : [(usize, usize, i64); n]
    }
    let answer = stack_block(&blocks, 0, 0);
    println!("{}", answer);
}

動的計画法

動的計画法でこういったものを解くときはブロックを1つずつ追加していくループを回すのが基本である。また、新しいブロックを下に追加する時、考えないといけないのは既に積み上がっているブロックの重さの合計が、新しいブロックの丈夫さを越えないかどうかである。このため、 $i$ 個のブロックを積み上げ、重さが $k$ の塔の価値の合計を $\textrm{dp}[i][k]$ とすれば良い。

$k$ は下にブロックを追加するためには、 $\max{s}$ 以下である必要があり、そこから最大 $\max{w}$ のブロックを追加する可能性があるので、 $0\leq k \leq \max{w} + \max{s}$ となる。問題からいくと20,000以下。コードにすると以下のようになる。計算量は $O(n)$ 。

let mut dp = vec![0; s_max + w_max + 1];
for (w, s, v) in blocks {
    let mut next_dp = dp.clone();
    for i in 0..=s {
        chmax!(next_dp[i + w], dp[i] + v);
    }
    dp = next_dp;
}

ただ、これだけでは答えはでてこない。処理としては $i$ 番目のブロックを $i-1$ 番目までのブロックで作ったタワーの下に入れるか入れないかを決めているため、処理するブロックの順番が大事になる。積み上げたブロックの価値は、各ブロックの価値の合計なので順番は関係ないが、積めるか積めないかの判断が順番に依存する。例えば、ブロック $a \rightarrow b$ の順番で処理する場合、 $a$ が $b$ の上には積めないのに、 $b$ が $a$ の上に積める場合そのケースは処理されない。つまり、 $a$ が $b$ の上に積めない時、 $b$ は必ず $a$ の上に積めない順番で処理する必要がある。式で書くと以下のようになる。

s_b < X + w_a \implies s_a < X + w_b

$X$ は $a,b$ 以外のブロックの重さであり、任意の数なので、 $X$ について解くと

\begin{align*} s_b - w_a < X &\implies s_a - w_b < X \\ s_a - w_b &\leq s_b - w_a \\ s_a + w_a &\leq s_b + w_b \end{align*}

なので、 $s + w$ でソートしてから処理すれば良いことが分かる。ソースコードは以下の通り。

main_dp.rs

use proconio::input;
use std::cmp;

fn main() {
    input! {
        n : usize, 
        mut blocks : [(usize, usize, i64); n]
    }

    let (w_max, s_max) = blocks.iter().fold((usize::MIN, usize::MIN), |(wm, sm), (w, s, _)| (cmp::max(wm, *w), cmp::max(sm, *s)));
    blocks.sort_by(|(wa, sa, _), (wb, sb, _)| (wa + sa).cmp(&(wb + sb))); 

    let mut dp = vec![0; s_max + w_max + 1];
    for (w, s, v) in blocks {
        let mut next_dp = dp.clone();
        for i in 0..=s {
            chmax!(next_dp[i + w], dp[i] + v);
        }
        dp = next_dp;
    }

    let answer = dp.iter().max().unwrap();
    println!("{}", answer);

測定結果

ブロックの数と処理時間の関係を計測した結果が以下のグラフである。

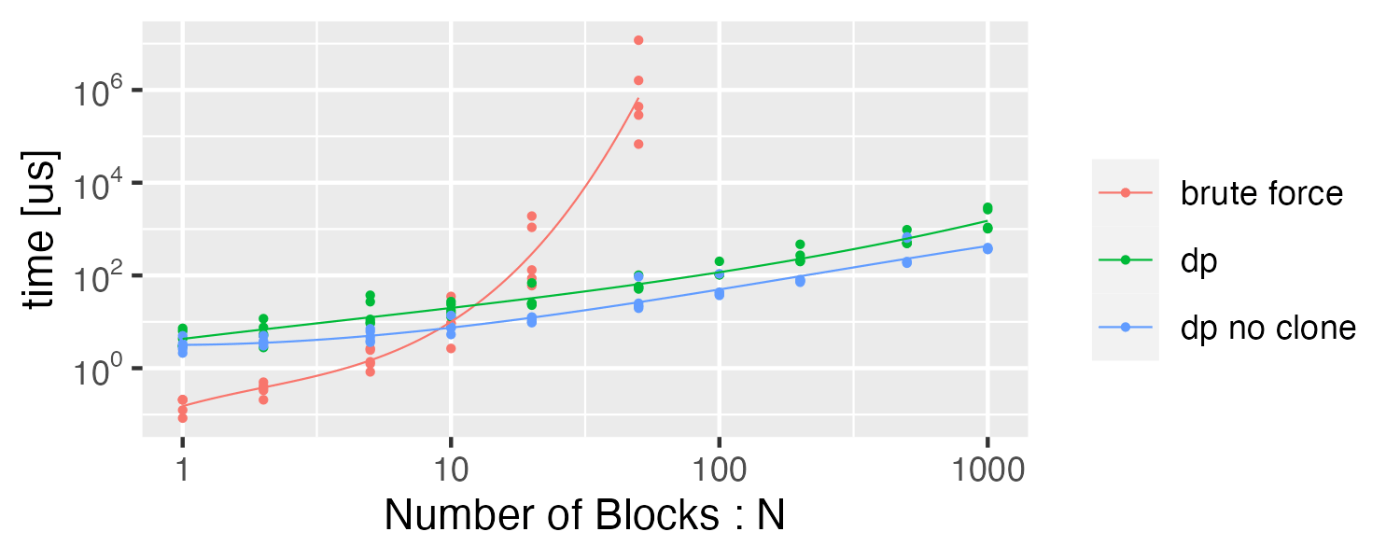
総当たり（brute force）が $N=50$ で発散気味であるのに対し、動的計画法（dp）だと線形になっている。ただ、 $N=10$ 以下だと総当たりの方が速い。

今回、2つのベクタを使って処理したが、for文の順番さえ気をつければ1本のベクタで処理できる。この時、clone()分の処理は軽くなる。ただ、処理自体は $N$ に依存しないので、一定時間速くなるだけである。

    for (w, s, v) in blocks {
-
+        for i in (0..=s).rev() {
            chmax!(dp[i + w], dp[i] + v);
        }
-
    }

Rustで動的計画法：Tower

はじめに

利用したライブラリ

解き方

総当たり

動的計画法

測定結果

関連記事

Discussion