🪐

【Plotly】水素原子の図鑑：電子波動関数の可視化

2022/09/30に公開

Python

0.概要

この記事ではシュレディンガー方程式に従う水素原子の電子波動関数の可視化方法について解説し、水素原子の図鑑を作成した。グラフィックライブラリとして、インタラクティブなグラフ描画が可能なPlotly(参考[1])を使用する。この記事ではPythonからPlotlyを使用するが、PlotlyはJulia, Matlab, R, Javascriptなどからも呼び出し可能である。

Plotlyには4次元データの可視化に優れたplotly.graph_objects.Volume() (3D Volume Plots)というモジュールがあり(参考[2,3])、今回はこれを利用する。ここでいう4次元データとは、3次元デカルト座標系で定義されるスカラー場のことを指す。温度場 $T(x,y,z)$ 、密度場 $\rho(x,y,z)$ などもこれに相当し、これらは引数が $x,y,z$ の3次元あり、戻り値が1次元(スカラー量)のため、合計4次元のデータとなる。

図1. Plotlyの3D Volume Plots描画例：電子波動関数 $\Psi_{nlm}(x, y, z), \ \ (n=5,l=2,m=-1)$

一般に、シュレディンガー方程式に従う波動関数 $\Psi(x,y,z)$ は複素数のため、戻り値は $\Psi(x,y,z)$ の実部と虚部の2次元あり、引数の $x,y,z$ を加えると、合計5次元のデータを取り扱う必要がある。ただ、電子スピンを考慮しない非相対論的ハミルトニアンで記述される水素原子の電子波動関数 $\Psi(x,y,z)$ は基底関数の取り換えで実数化することができ、戻り値を1次元にすることができる。今回は実数化された電子波動関数 $\Psi(x,y,z)$ を3次元デカルト座標系 $(x,y,z)$ で表示する方法について解説し、水素原子の図鑑を作成した。

実数化された電子波動関数 $\Psi(x,y,z)$ を3次元空間内で可視化する方法として、下記の3つの方法が考えられる。

点描で電子雲を表現する( $\Psi(x,y,z)$ の大きさを点の密度として捉え、散布図を描く)
$\Psi(x,y,z)=A_0$ を満たすような等値面を描画する( $A_0$ は $x,y,z$ に依存しない定数)
$\Psi(x,y,z)$ を例えば $z=0$ 平面上で等高線プロットする(コンター図を描く)。

1、2に共通する問題点として、 $\Psi(x,y,z)$ が球対称分布を取るとき(方位量子数と磁気量子数が0のとき)、 $(x,y,z)$ の原点に近いところの情報が見えにくいということが挙げられる。2の方法に至っては等値面の内側の情報は全く見えない。2、3に共通する問題として、4次元データを3次元データへと次元を落とした描画法で、情報量が足りない場合がある。

Plotlyのplotly.graph_objects.Volume()を用いた描画も完全な描画方法ではないものの、1~3の描画方法の短所を上手く補うことができる。plotly.graph_objects.Volume()は、2の描画方法を発展させたもので、等値面を多数描画し、それぞれの等値面を半透明化することで、 $\Psi(x,y,z)$ の内部情報(原点に近い部分の情報)の描画を可能にしつつ、次元の削減による情報の消失を最小限に抑えた描画方法である。図2にその描画例を示す。

ただ、この描画方法はインタラクティブな描画になっていることと、多数の等値面を描画する必要があるため、描画自体に時間がかかるという短所がある。具体的な計算条件は後述するが(3.1節)、私の計算環境だと1つのグラフを出力するまでに約25秒かかった。電子波動関数の計算自体は約1秒で終了しており、グラフの描画自体にかかった時間は約24秒である。全体の計算時間のうち95%以上がグラフの描画にかかった時間に占められる。

図2. 内部情報の可視化例：電子波動関数 $\Psi_{nlm}(x, y, z), \ \ (n=3,l=0,m=0)$

1.可視化する関数：水素原子の電子波動関数

定常状態において、主量子数 $n$ 、方位量子数 $l$ 、磁気量子数 $m$ を取るときの水素原子の電子波動関数 $\Psi_n^{lm}(r,\theta,\phi)$ は、式(1)のようなシュレディンガー方程式に従う。 $\hat{H}$ は電子スピンを考慮しない非相対論的ハミルトニアンで、式(2)のようになる。このとき原子核と電子の相互作用はクーロンポテンシャルとして取り扱っている。原子系のような球対称ポテンシャルを取り扱う問題では、波動関数 $\Psi$ の引数として3次元極座標のパラメータである $r, \theta, \phi$ を採用することが多く、ここでもその流儀に従っている。

\begin{align} &\hat{H} \Psi_n^{lm}(r,\theta,\phi) = E_{n} \Psi_n^{lm}(r,\theta,\phi)\\ &\begin{split} &\hat{H} = -\frac{\hbar^2}{2\mu} \left\{ \frac{1}{r} \frac{\partial^2}{\partial^2}r + \frac{1}{r^2 \rm sin\theta} \frac{\partial}{\partial \theta}\left( \rm sin\theta \frac{\partial}{\partial \theta} \right) + \frac{1}{r^2 \rm sin^2 \theta} \frac{\partial^2}{\partial \phi^2} \right\} -\frac{e^2}{r} \\ &\mu = \frac{m_e m_p}{m_e + m_p} \end{split} \end{align}

式(1)のようなシュレディンガー方程式は解析的に解くことができ、 $\Psi_n^{lm}(r,\theta,\phi)$ は動径波動関数 $R_{nl}(r)$ と球面調和関数 $Y_l^m (\theta, \phi)$ を用いて式(3)のようにあらわせる。動径波動関数 $R_{nl}(r)$ はラゲール陪多項式 $L_i^j(x)$ を用いて、式(4)~(6)のようにあらわせる。球面調和関数 $Y_l^m (\theta, \phi)$ はルジャンドル陪多項式 $P_l^m(x)$ とルジャンドル多項式 $P_l(x)$ を用いて、式(7)~(10)のようにあらわせる。ここで、 $n,l,m$ は式(11)を満たす整数である。

\begin{align} \Psi_n^{lm}(r,\theta,\phi) &= R_{nl}(r) \times Y_l^m (\theta, \phi) \\ R_{nl} (r) &= -\left\{ \left(\frac{2}{na_0} \right)^3 \frac{(n-l-1)!}{2n \left[ \left(n+l\right)!\right]^3} \right\}^{1/2} \cdot {\rm exp}\left(\frac{1}{2}\zeta\right) \cdot \zeta^l \cdot L_{n+l}^{2l+1} (\zeta) \\ a_0 &= \frac{\hbar}{\mu e^2},\ \ \ \zeta = \frac{2}{n a_0}r,\ \ \ \mu = \frac{m_e m_p}{m_e + m_p} \\ L_i^j(x) &= \sum_{k=0}^{i-j} (-1)^{k+j} \frac{(i!)^2}{k!(k+j)!(i-k-j)!}x^k \\ Y_l^m(\theta, \phi) &= \epsilon \sqrt{\frac{2l+1}{4\pi}\cdot \frac{(l-|m|)!}{(l+|m|)!}}P_l^m({\rm cos}\theta)e^{im\phi} \\ \epsilon &= \begin{cases} (-1)^m &(m > 0) \\ 1 &(m \leq 0)\\ \end{cases}\\ P_l^m(x) &= (1-x^2)^{\frac{|m|}{2}} \frac{d^{|m|}}{dx^{|m|}} P_l(x)\\ P_l(x) &= \frac{1}{2^l l!}\frac{d^l}{dx^l}(x^2-1)^l\\ &\begin{cases} 1 \leq n \\ 0 \leq l \leq n-1 \\ -l \leq m \leq l \\ \end{cases}\\ \end{align}

式(3)~(11)であらわされる電子波動関数 $\Psi_n^{lm}(r,\theta,\phi)$ は $m \ne 0$ のとき、球面調和関数 $Y_l^m (\theta, \phi)$ が複素数となるため5次元データとなり描画が困難になる。球面調和関数 $Y_l^m (\theta, \phi)$ からなる基底関数系は、式(12)のように基底変換することで実数化することができる。実数化することで次元が一つ減り、電子波動関数が4次元データとなるため、可視化が可能になる。このとき、基底関数系 $\{Y_l^m (\theta, \phi)\}$ が持っていた完全性や正規直交性は、実数化された基底関数系 $\{Y_{lm} (\theta, \phi)\}$ へと遺伝される。

\begin{align} Y_{lm}(\theta, \phi) = \begin{cases} \frac{i}{\sqrt 2}\left(Y_l^{-|m|}(\theta, \phi) + (-1)^{|m|+1} \cdot Y_l^{|m|}(\theta, \phi) \right) & (m<0)\\ Y_l^{m}(\theta, \phi) & (m = 0)\\ \frac{1}{\sqrt 2}\left(Y_l^{-m}(\theta, \phi) + (-1)^{m} \cdot Y_l^{m}(\theta, \phi) \right) & (m>0) \end{cases}\\ \end{align}

実数化された球面調和関数 $Y_{lm} (\theta, \phi)$ を用いて、電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ を式(13)のようにあらわせば、電子波動関数は式(11)を満たす全ての整数 $n,l,m$ に対し、実数関数となる。このとき、実数化された球面調和関数 $Y_{lm} (\theta, \phi)$ は、複素数の球面調和関数 $Y_l^m (\theta, \phi)$ の線形結合としてあらわされているため、式(13)であらわされる電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ は元のシュレディンガー方程式、式(1)を満たす。本記事では式(13)であらわされる実数化された電子波動関数を描画する。

また、本論とはあまり関係はないが、 $\Psi_n^{lm}(r,\theta,\phi)$ は3つの演算子 $\hat{H}, \hat{L^2}, \hat{L_z}$ の同時固有関数であったのに対し、実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ は $m=0$ の場合を除き、2つの演算子 $\hat{H}, \hat{L^2}$ のみの同時固有関数になっており、 $\hat{L_z}$ の固有関数にはなっていないことに注意したい。これは球面調和関数を実数化する際に基底変換をしたためである。

\begin{align} \Psi_{nlm}(r,\theta,\phi) &= R_{nl}(r) \times Y_{lm} (\theta, \phi) \end{align}

2.プログラム

本記事で使用したプログラムの全文は下記である。PlotlyはPythonから呼び出している。プログラムの説明は、「2-1.電子波動関数の計算」と「2-2.グラフの描画」に分けて行う。下記のプログラムは主量子数 $n$ 、方位量子数 $l$ 、磁気量子数 $m$ を指定すると、それらの量子数に応じた1枚のグラフが出力される。量子数 $n,l,m$ の値には式(11)を満たす任意の整数を指定できる。

下記のプログラムを使用する上での注意点は、 $x=y=z=0$ または $x=y=0$ を満たす計算点を含むような領域分割を行った場合、ゼロ割りが発生し正常なグラフ出力ができない。プログラムを修正すればこの問題は解決するが、今回はそこまで行わなかった。そもそもゼロ割りが発生しうるようなプログラムを書かなければならなくなった理由は「2-2.グラフの描画」で説明する。

プログラムの全文

# 電子波動関数の計算に必要なモジュール
import numpy as np
from scipy.special import sph_harm
from scipy.special import factorial
from scipy.special import assoc_laguerre
# グラフの描画に必要なモジュール
import plotly.graph_objects as go
import plotly.io as pio
#pio.renderers.default='svg'
pio.renderers.default='browser'

#動径波動関数
def R_nl(r, n, l):
    
    a0 = 1.0
    zeta = 2.0/n/a0 * r
    
    #修正係数
    n_d = n-l-1
    L_coff = (-1)**(2*l+1) * factorial(n+l)
    
    f_coff = - ((2.0/n/a0)**3 * factorial(n-l-1)/2.0/n/factorial(n+l)**3)**(1.0/2.0)
    f = f_coff * np.exp(-zeta/2.0) * zeta**l * L_coff * assoc_laguerre(zeta, n_d, 2*l+1)
    
    return f

# 球面調和関数のノーテーションや文字を物理の教科書用にカスタマイズ
def my_sph_harm(l, m, theta, phi):
    return sph_harm(m, l, phi, theta)

# 実数化した球面調和関数を算出する関数：関数の中でmy_sph_harm()使用
def real_sph_harm(l, m, theta, phi):
    
    if m < 0:
        # m < 0であることに注意: np.fabs(m) = -m
        Y = np.real(1.j * np.sqrt(1/2) * (my_sph_harm(l,m, theta, phi) + (-1)**(-m+1) * my_sph_harm(l, -m, theta, phi)))
    if m == 0:
        Y = np.real(my_sph_harm(l, m, theta, phi))
    if m > 0:
        Y = np.real(np.sqrt(1/2) * (my_sph_harm(l,-m, theta, phi) + (-1)**m * my_sph_harm(l, m, theta, phi)))
    
    return Y

# 量子数の指定
n = 5 # 主量子数: 1 <= n
l = 4 # 方位量子数 0 <= l <= n-1
m = 0 # 磁気量子数 -l <= m <= l

# 計算領域設定
N = 60 # 分割数
xmin, ymin, zmin = -50, -50, -50
xmax, ymax, zmax =  50,  50,  50

# メッシュ作成
x_a = np.linspace(xmin,xmax,N)
y_a = np.linspace(ymin,ymax,N)
z_a = np.linspace(zmin,zmax,N)
x, y, z = np.meshgrid(x_a, y_a, z_a)

# 極座標化
r = np.sqrt(x**2+y**2+z**2)
theta = np.arccos(z/r)
phi = np.sign(y) * np.arccos(x/np.sqrt(x**2 + y**2))

# 電子波動関数の計算
R_wave = R_nl(r, n, l) # 動径波動関数
Y_wave = real_sph_harm(l, m, theta, phi) # 実数化された球面調和関数
psi = R_wave * Y_wave # 実数化された電子波動関数

# 配列の1次元化
X = x.flatten()
Y = y.flatten()
Z = z.flatten()
Psi = psi.flatten()

# 描画する等値面の範囲設定
Max = np.maximum( np.fabs(np.amin(psi)), np.fabs(np.amax(psi)))
Max = 1/5 * Max

# グラフの描画
fig = go.Figure(data=go.Volume(
    x=X,
    y=Y,
    z=Z,
    value=Psi,
    isomin=-Max, # 描画する等値面の最小値
    isomax=Max, # 描画する等値面の最大値
    opacity=0.1, # 不透明度：0~1
    surface_count=20, # 描画する等値面の数
    opacityscale="extremes", # 不透明度のカスタマイズ
    ))

# グラフレイアウトの調整
fig.update_layout(
    scene = dict(
        xaxis = dict(backgroundcolor="rgb(0, 0, 0)"), # 黒背景
        yaxis = dict(backgroundcolor="rgb(0, 0, 0)"), # 黒背景
        zaxis = dict(backgroundcolor="rgb(0, 0, 0)"), # 黒背景
                ),
    scene_camera= dict(eye=dict(x=1.5, y=1.5, z=0.5)) # カメラアングル
                  )

# 図の表示
fig.show()

# グラフの保存
name = "psi" + str(n)
name = name + str(l)
name = name + str(m)
name = name + ".png"
fig.write_image(name)

2-1.電子波動関数の計算

実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ は、種々の特殊関数を用いて表現されている。下記は実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ の計算をしている部分を抜粋したものである。特殊関数の計算にはscipyの特殊関数計算モジュールを使用しているので、量子数 $n,l,m$ の値には式(11)を満たす任意の整数を指定できる。

電子波動関数の計算

# 電子波動関数の計算に必要なモジュール
import numpy as np
from scipy.special import sph_harm
from scipy.special import factorial
from scipy.special import assoc_laguerre
"""
~~~ 中略 ~~~
"""
#動径波動関数
def R_nl(r, n, l):
    
    a0 = 1.0
    zeta = 2.0/n/a0 * r
    
    #修正係数
    n_d = n-l-1
    L_coff = (-1)**(2*l+1) * factorial(n+l)
    
    f_coff = - ((2.0/n/a0)**3 * factorial(n-l-1)/2.0/n/factorial(n+l)**3)**(1.0/2.0)
    f = f_coff * np.exp(-zeta/2.0) * zeta**l * L_coff * assoc_laguerre(zeta, n_d, 2*l+1)
    
    return f

# 球面調和関数のノーテーションや文字を物理の教科書用にカスタマイズ
def my_sph_harm(l, m, theta, phi):
    return sph_harm(m, l, phi, theta)

# 実数化した球面調和関数を算出する関数：関数の中でmy_sph_harm()使用
def real_sph_harm(l, m, theta, phi):
    
    if m < 0:
        # m < 0であることに注意: np.fabs(m) = -m
        Y = np.real(1.j * np.sqrt(1/2) * (my_sph_harm(l,m, theta, phi) + (-1)**(-m+1) * my_sph_harm(l, -m, theta, phi)))
    if m == 0:
        Y = np.real(my_sph_harm(l, m, theta, phi))
    if m > 0:
        Y = np.real(np.sqrt(1/2) * (my_sph_harm(l,-m, theta, phi) + (-1)**m * my_sph_harm(l, m, theta, phi)))
    
    return Y

# 量子数の指定
n = 5 # 主量子数: 1 <= n
l = 4 # 方位量子数 0 <= l <= n-1
m = 0 # 磁気量子数 -l <= m <= l

# 計算領域設定
N = 60 # 分割数
xmin, ymin, zmin = -50, -50, -50
xmax, ymax, zmax =  50,  50,  50

# メッシュ作成
x_a = np.linspace(xmin,xmax,N)
y_a = np.linspace(ymin,ymax,N)
z_a = np.linspace(zmin,zmax,N)
x, y, z = np.meshgrid(x_a, y_a, z_a)

# 極座標化
r = np.sqrt(x**2+y**2+z**2)
theta = np.arccos(z/r)
phi = np.sign(y) * np.arccos(x/np.sqrt(x**2 + y**2))

# 電子波動関数の計算
R_wave = R_nl(r, n, l) # 動径波動関数
Y_wave = real_sph_harm(l, m, theta, phi) # 実数化された球面調和関数
psi = R_wave * Y_wave # 実数化された電子波動関数

2-1-1.動径波動関数の計算： $R_{nl}(r)$

本記事のプログラムでは、動径波動関数 $R_{nl}(r)$ を計算するための関数R_nl(r, n, l)を、下記のように定義している。動径波動関数 $R_{nl}(r)$ は、式(6)のようなラゲール陪多項式 $L_i^j(x)$ を用いてあらわされ、ラゲール陪多項式計算モジュールscipy.special.assoc_laguerre()はこの関数の中から呼び出している。

scipy.special.assoc_laguerre()を使用する際の注意点として、ノーテーションと係数の修正を式(14)のようにしていることが挙げられる。これは、式(6)のような一般的な量子力学の教科書でなされるラゲール陪多項式の定義とscipyでの定義が異なるためである。詳細については以前書いた記事(参考[4])でまとめたため、気になる方はそちらを参照されたい。

\begin{align} L_{n+l}^{2l+1} (x) &\rightarrow (-1)^{2l+1} \cdot (n+l)! \cdot L^{2l+1}_{n-l-1} (x) \end{align}

動径波動関数の計算

#動径波動関数
def R_nl(r, n, l):
    
    a0 = 1.0
    zeta = 2.0/n/a0 * r
    
    #修正係数
    n_d = n-l-1
    L_coff = (-1)**(2*l+1) * factorial(n+l)
    
    f_coff = - ((2.0/n/a0)**3 * factorial(n-l-1)/2.0/n/factorial(n+l)**3)**(1.0/2.0)
    f = f_coff * np.exp(-zeta/2.0) * zeta**l * L_coff * assoc_laguerre(zeta, n_d, 2*l+1)
    
    return f

2-1-2.球面調和関数の計算： $Y_l^m (\theta, \phi)$ と $Y_{lm} (\theta, \phi)$

球面調和関数 $Y_l^m (\theta, \phi)$ (一般には複素数)の計算は、下記のような関数my_sph_harm(l, m, theta, phi)で行っている。my_sph_harm(l, m, theta, phi)の戻り値はscipyの球面調和関数計算モジュールscipy.special.sph_harm(m, l, phi, theta)である。この記事のプログラムではmy_sph_harm(l, m, theta, phi)を使用し、ノーテーション $l,m$ と引数 $\theta, \phi$ の入れ替えをしている。

このような処理をしている理由は、一般的な資料では球面調和関数は式(7)~(10)のように定義されているが、scipy.special.sph_harm()での定義は一般的なものと異なるからである。球面調和関数の定義の違いの詳細については、以前書いた記事(参考[5])でまとめたため、気になる方はそちらを参照されたい。

球面調和関数の計算

# 球面調和関数のノーテーションや文字を物理の教科書用にカスタマイズ
def my_sph_harm(l, m, theta, phi):
    return sph_harm(m, l, phi, theta)

実数化された球面調和関数 $Y_{lm} (\theta, \phi)$ の計算は、下記のような関数real_sph_harm(l, m, theta, phi)で行っている。実数化の手続きは式(11)に従う。この関数内では関数my_sph_harm(l, m, theta, phi)を呼び出しており、関数my_sph_harm(l, m, theta, phi)では $Y_l^m (\theta, \phi)$ (一般には複素数)の計算をしている。

実数化された球面調和関数の計算

# 実数化した球面調和関数を算出する関数：関数の中でmy_sph_harm()使用
def real_sph_harm(l, m, theta, phi):
    
    if m < 0:
        # m < 0であることに注意: np.fabs(m) = -m
        Y = np.real(1.j * np.sqrt(1/2) * (my_sph_harm(l,m, theta, phi) + (-1)**(-m+1) * my_sph_harm(l, -m, theta, phi)))
    if m == 0:
        Y = np.real(my_sph_harm(l, m, theta, phi))
    if m > 0:
        Y = np.real(np.sqrt(1/2) * (my_sph_harm(l,-m, theta, phi) + (-1)**m * my_sph_harm(l, m, theta, phi)))
    
    return Y

2-1-3.計算領域の設定とメッシュ分割

メインプログラムの下記箇所で計算領域の設定と、 $(x,y,z)\rightarrow(r,\theta,\phi)$ のような変数変換をしている。 $(x,y,z)\rightarrow(r,\theta,\phi)$ のような変数変換をする際、 $\theta$ の算出に $z/r$ の計算をするが、 $x=y=z=0$ のとき $r=0$ となりゼロ割りが発生し、正常なグラフ描画ができない。また、 $\phi$ の算出の際は、 $x/\sqrt{x^2+y^2}$ の計算をするが、 $x=y=0$ のときゼロ割りが発生し正常なグラフ描画ができない。例えば下記の場合はN=51と設定するとゼロ割りが発生する。if文等を使ってゼロ割りを回避することもできるが、プログラムが複雑化するため、今回はそこまでしなかった。

計算領域の設定と極座標化

# 計算領域設定
N = 60 # 分割数
xmin, ymin, zmin = -50, -50, -50
xmax, ymax, zmax =  50,  50,  50

# メッシュ作成
x_a = np.linspace(xmin,xmax,N)
y_a = np.linspace(ymin,ymax,N)
z_a = np.linspace(zmin,zmax,N)
x, y, z = np.meshgrid(x_a, y_a, z_a)

# 極座標化
r = np.sqrt(x**2+y**2+z**2)
theta = np.arccos(z/r)
phi = np.sign(y) * np.arccos(x/np.sqrt(x**2 + y**2))

プログラムの上記箇所について、 $\Psi(r,\theta,\phi)$ の引数は $(r,\theta,\phi)$ であるため、例えば下記のように記述するのがゼロ割りも発生しない素直なプログラムである。しかし、Plotlyの描画モジュールplotly.graph_objects.Volume()(プログラム中ではgo.Volume()と記述)へ渡す引数との関係から、今回はこのような不格好なプログラムを組まざるを得なかった。plotly.graph_objects.Volume()の仕様については、後述の「2-2.グラフの描画」で解説する。

本来書きたいプログラム

# 計算領域設定
N = 60 # 分割数
r_min, theta_min, phi_min = 0, 0, 0
r_max, theta_max, phi_max = 50, np.pi, 2*np.pi

# メッシュ作成
r_a     = np.linspace(r_min,r_max,N)
theta_a = np.linspace(theta_min,theta_max,N)
phi_a   = np.linspace(phi_min,phi_max,N)
r, theta, phi = np.meshgrid(r_a, theta_a, phi_a)

2-2.グラフの描画

全体のプログラムの内、グラフの描画に必要な箇所のみ下記に抜粋した。説明が必要と思われる箇所には適宜説明を入れる。また、今回はPlotlyのplotly.graph_objects.Volume()モジュール(参考[2,3])で等値面を多数描画したが、このモジュールは体積レンダリング用のモジュールである。一方で、plotly.graph_objects.Isosurface()という等値面自体を描くことを目的とした、ほぼ同等機能を持つモジュールもPlotlyには存在する(参考[6])。

両者の使用方法や得られるグラフはほぼ同じであるが、plotly.graph_objects.Volume()はオプショナルパラメータとしてopacityscaleを設定できる。opacityscaleは等値面の不透明度に関係するパラメータで、詳しくは後述するが、plotly.graph_objects.Volume()は等値面ごとに不透明度を細かく設定でき、体積レンダリングの際(今回のように4次元データの可視化をする際)は、深さ方向の視認性に優れる。

また、等値面を1枚描くだけで十分な場合はplotly.graph_objects.Surface()を使えば良い(参考[7])。ただこの場合、Plotlyを使うまでも無く、matplotlibのplot_surface()でも十分目的は達成できる。

グラフの描画に必要な箇所

# グラフの描画に必要なモジュール
import plotly.graph_objects as go
import plotly.io as pio
#pio.renderers.default='svg'
pio.renderers.default='browser'
"""
~~~ 中略 ~~~
"""
# 配列の1次元化
X = x.flatten()
Y = y.flatten()
Z = z.flatten()
Psi = psi.flatten()

# 描画する等値面の範囲設定
Max = np.maximum( np.fabs(np.amin(psi)), np.fabs(np.amax(psi)))
Max = 1/5 * Max

# グラフの描画
fig = go.Figure(data=go.Volume(
    x=X,
    y=Y,
    z=Z,
    value=Psi,
    isomin=-Max, # 描画する等値面の最小値
    isomax=Max, # 描画する等値面の最大値
    opacity=0.1, # 不透明度：0~1
    surface_count=20, # 描画する等値面の数
    opacityscale="extremes", # 不透明度のカスタマイズ
    ))

# グラフレイアウトの調整
fig.update_layout(
    scene = dict(
        xaxis = dict(backgroundcolor="rgb(0, 0, 0)"), # 黒背景
        yaxis = dict(backgroundcolor="rgb(0, 0, 0)"), # 黒背景
        zaxis = dict(backgroundcolor="rgb(0, 0, 0)"), # 黒背景
                ),
    scene_camera= dict(eye=dict(x=1.5, y=1.5, z=0.5)) # カメラアングル
                  )

# 図の表示
fig.show()

# グラフの保存
name = "psi" + str(n)
name = name + str(l)
name = name + str(m)
name = name + ".png"
fig.write_image(name)

2-2-1.Spyder上から実行する場合の設定

私はAnacondaが提供するPythonの統合開発環境であるSpyder上でプログラムを実行したが、SpyderからPlotlyを使用する際は下記の記述が必要である。pio.renderers.default='browser'のように記述すると、グラフがブラウザ上に描画される。pio.renderers.default='svg'と記述すると、Spyderのプロット画面上にグラフが描画される。pio.renderers.default='svg'とした場合は、グラフのインタラクティブ機能は使えない。これはstack overflowの記事(参考[8])を参考にした。

Spyder上でPlotlyを使用するための設定

import plotly.io as pio
#pio.renderers.default='svg'
pio.renderers.default='browser'

2-2-2.引数の仕様：plotly.graph_objects.Volume()

現時点では問題の切り分けが明確にできていないが、plotly.graph_objects.Volume()へ渡す引数の仕様(条件)に関し、下記3点の注意事項がある。1.に関しては公式ヘルプに明確に記載があり、仕様として明らかである(参考[2,3])。2,3.の仕様については、私の推測に基づくもので、「2-1.電子波動関数の計算」で言及した、ゼロ割りが発生しうるようなプログラムを書かざるを得なくなった理由にも関係する。2,3.の仕様については未検証な部分が現時点では多く残る。

引数は1次元配列である必要がある
引数の1次元配列は規則的な数列になっていなければならない(例えばxの値の昇順など)
引数の1次元配列は立方体メッシュから生成されたものでなければならない

まずは1.の仕様について解説する。本記事のプログラムでは下記のように.flatten()で3次元配列を1次元化してplotly.graph_objects.Volume()(プログラム中ではgo.Volume()と記述)に渡している。pythonなどのスクリプト言語を使用する際は、np.meshgrid()などで作成した3次元配列x, y, z, phiをplotly.graph_objects.Volume()に直接引数として渡したくなるが、仕様としてそれは許されていない。

3次元配列の1次元配列化

# 計算領域設定
N = 60 # 分割数
xmin, ymin, zmin = -50, -50, -50
xmax, ymax, zmax =  50,  50,  50

# メッシュ作成
x_a = np.linspace(xmin,xmax,N)
y_a = np.linspace(ymin,ymax,N)
z_a = np.linspace(zmin,zmax,N)
x, y, z = np.meshgrid(x_a, y_a, z_a)
"""
~~~ 中略 ~~~
"""
# 配列の1次元化
X = x.flatten()
Y = y.flatten()
Z = z.flatten()
Psi = psi.flatten()
"""
~~~ 中略 ~~~
"""
# グラフの描画
fig = go.Figure(data=go.Volume(
    x=X,
    y=Y,
    z=Z,
    value=Psi,
    isomin=-Max, # 描画する等値面の最小値
    isomax=Max, # 描画する等値面の最大値
    opacity=0.1, # 不透明度：0~1
    surface_count=20, # 描画する等値面の数
    opacityscale="extremes", # 不透明度のカスタマイズ
    ))

次は2,3.の仕様について解説する。今回の目的は、実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ をデカルト座標系 $(x,y,z)$ で描画することである。一方、 $\Psi_{nlm}(r,\theta,\phi)$ の直接の引数は $(r,\theta,\phi)$ であるため、下記のようにnp.meshgrid()などで $(r,\theta,\phi)$ のメッシュを生成し、その $(r,\theta,\phi)$ で $\Psi_{nlm}(r,\theta,\phi)$ の計算をした後に、デカルト座標 $(x,y,z)$ に変換するのが素直で自然である。この方法をとれば、「2-1.電子波動関数の計算」で言及したようにゼロ割りによる不都合も生じない。

ただ、この方法でplotly.graph_objects.Volume()に値を渡すと空のグラフが生成され、意図した描画ができない。前述した通り、公式ドキュメントにはplotly.graph_objects.Volume()の引数が満たすべき仕様について細かい記載がない(参考[2,3])。そのため、本記事のプログラムではゼロ割りが発生しうるような不格好な方法をとっている。

また、この問題に最も近い記事がstack overflowにあったが、スマートな解決方法は提示されていなかった(参考[9])。stack overflowに記載される投稿者の疑問は、本記事の疑問とは少し異なるが、この記事の投稿者はPlotlyを使用することを諦めて、MayaViという別のグラフ描画ライブラリ(参考[10,11])を使用することで問題が解決したと報告していた。

今回はMayaViを実際に使用して確認するまでには至らなかったが、公式ドキュメントのサンプルコードを読む限り、MayaViのmayavi.mlab.contour3d()モジュールではPlotlyのplotly.graph_objects.Volume()モジュールとほぼ同等のことができることは確認できた(参考[12,13])。また、MayaViのmayavi.mlab.contour3d()モジュールではnp.meshgrid()で生成した3次元配列を直接引数に取ることができることも、サンプルコードから確認できた。一方、下記コードのような極座標メッシュを取り扱うことが可能かまでは確認できなかった。

本来書きたいプログラム

# 計算領域設定
N = 60 # 分割数
r_min, theta_min, phi_min = 0, 0, 0
r_max, theta_max, phi_max = 50, np.pi, 2*np.pi

# メッシュ作成
r_a     = np.linspace(r_min,r_max,N)
theta_a = np.linspace(theta_min,theta_max,N)
phi_a   = np.linspace(phi_min,phi_max,N)
r, theta, phi = np.meshgrid(r_a, theta_a, phi_a)
"""
~~~ 中略:psiの計算 ~~~
"""
# デカルト座標化
x = r * np.sin(theta) * np.cos(phi)
y = r * np.sin(theta) * np.sin(phi)
z = r * np.cos(theta)

# 配列の1次元化
X = x.flatten()
Y = y.flatten()
Z = z.flatten()
Psi = psi.flatten()
"""
~~~ 中略 ~~~
"""
# グラフの描画
fig = go.Figure(data=go.Volume(
    x=X,
    y=Y,
    z=Z,
    value=Psi,
    isomin=-Max, # 描画する等値面の最小値
    isomax=Max, # 描画する等値面の最大値
    opacity=0.1, # 不透明度：0~1
    surface_count=20, # 描画する等値面の数
    opacityscale="extremes", # 不透明度のカスタマイズ
    ))

2-2-3.等値面の描画設定：plotly.graph_objects.Volume()

描画する等値面の設定に関する説明をここで行う。plotly.graph_objects.Volume()の引数として、isominとisomaxを指定することで描画する等値面の最小値と最大値を陽に指定することができる。isominとisomaxはオプショナルパラメータで、指定しなければvalueの最小値と最大値の範囲で等値面が描画される。

下記プログラムではMax = 1/5 * Maxとして等値面の描画範囲を狭めているが、これは電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ の値の大きなところと小さなところの差が大きく、値の小さい等値面が殆ど見えなくなってしまうためである。見た目の問題なのでMax = 1/5 * Maxのようにしなくても別に良い。

opacityは等値面の不透明度を指定するパラメータで、0から1の範囲で値を代入する。1に近いほど等値面は不透明になる。具体的にどういう値を代入するかは、考えている問題や描画する等値面の数によって異なるため解析者が自分で決めなければならない。今回はopacity=0.1とした。

opacityscaleも等値面の不透明度を指定するパラメータで、等値面の値に応じて不透明度を変更できる。opacityscale="extremes"と指定すると、等値面の最小値と最大値で最も不透明度が上がり、真ん中の等値面で最も不透明度が下がる。つまり、等値面の最小値と最大値が強調された描画となる。opacityscale="uniform"と指定すると、全ての等値面で均一な不透明度となる。図3にextremesとuniformの違いを示す。opacityscaleに二次元配列のテーブルデータを代入し、より柔軟性を持たせた不透明度の設定もできるが詳細は公式ヘルプを参照されたい(参考[2,3])。また、opacityscaleを指定できるか否かがplotly.graph_objects.Volume()とplotly.graph_objects.Isosurface()の大きな違いである。

surface_countは描画する等値面の数を指定するパラメータで、大きな値を指定するほど体積レンダリングの性能は上がるが、同時にopacityを適切に設定しないと内部情報が見えにくくなる。また、surface_countに大きな値を指定するとグラフの描画完了までに時間がかかる。今回はsurface_count=20とし、20枚の等値面を描画している。

また、今回は特に設定していないが、colorscale="jet"のように指定することで等値面の色を変更できる。デフォルトで用意されているカラーパレットは参考[14]の記事でまとめられている。

描画する等値面に関する設定

# 描画する等値面の範囲設定
Max = np.maximum( np.fabs(np.amin(psi)), np.fabs(np.amax(psi)))
Max = 1/5 * Max

# グラフの描画
fig = go.Figure(data=go.Volume(
    x=X,
    y=Y,
    z=Z,
    value=Psi,
    isomin=-Max, # 描画する等値面の最小値
    isomax=Max, # 描画する等値面の最大値
    opacity=0.1, # 不透明度：0~1
    surface_count=20, # 描画する等値面の数
    opacityscale="extremes", # 不透明度のカスタマイズ
    ))

図3. "extremes"と"uniform"の比較（電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=3,l=1,m=0$ ）

2-2-4.グラフレイアウトの調整

グラフ背景色はsceneのbackgroundcolorにRGB値を指定することで変更できる(参考[15])。デフォルトでは淡い青色に設定されている。今回は黒色の背景に変更している。

カメラアングル(視点位置と視点方向)はscene_cameraのeyeにベクトル値を指定することで変更できる(参考[16])。デフォルト値はx=1.25, y=1.25, z=1.25である。今回は静止画保存も行っているためこの設定も行っているが、インタラクティブなグラフ描画のみをする場合は、指定する意味があまりない。

グラフレイアウトの調整

# グラフレイアウトの調整
fig.update_layout(
    scene = dict(
        xaxis = dict(backgroundcolor="rgb(0, 0, 0)"), # 黒背景
        yaxis = dict(backgroundcolor="rgb(0, 0, 0)"), # 黒背景
        zaxis = dict(backgroundcolor="rgb(0, 0, 0)"), # 黒背景
                ),
    scene_camera= dict(eye=dict(x=1.5, y=1.5, z=0.5)) # カメラアングル
                  )

3.計算結果

3-1.計算時間

今回は $60\times60\times60=216,000$ 個の計算点で、実数化された波動関数 $\Psi_{nlm}(r,\theta,\phi)$ の計算をした。また、1つのグラフで20枚の等値面を描画した。私の計算環境では、1つのグラフ出力完了までに約25秒かかった。この内、 $\Psi_{nlm}(r,\theta,\phi)$ の計算に約1秒かかり、グラフの描画自体には約24秒かかった。全体の計算時間のうち95%以上がグラフの描画にかかった時間に占められる。このとき、特別な並列計算などは行っていない。

$\Psi_{nlm}(r,\theta,\phi)$ の計算の方は、Juliaなどのもっと早く動作するプログラミング言語への変更や並列計算で計算時間の短縮が見込めるが、この部分の計算にはそもそも約1秒程度しか計算時間がかかっていないため、ここを高速化してもその効果は薄い。

グラフの描画の際、pythonからplotly.graph_objects.Volume()を呼び出しhtmlファイルを出力する。Plotlyの動作仕様を正しく把握できていないが、plotly.graph_objects.Volume()の動作の際は裏でJavascriptが動作していると推定される。そのため、pythonよりも早く動作するプログラミング言語からPlotlyを呼び出しても、おそらく計算速度は劇的に速くならないし、並列計算などのソフト的処理で高速化が見込めるかについては私の知識不足で不明である。単純にハードのマシンスペックを上げるか、別のグラフ描画ライブラリを使用するしか有効な高速化方法は無いように思える。

3-2.電子波動関数(静止画)

実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ の計算結果を図4~7に示す。図5~7には拡大図を付けた（それぞれ、図5-1~5-4, 6-1~6-9, 7-1~16）。今回は $n=1,2,3,4$ の場合の結果についてまとめた。妥当な計算結果が得られているかの確認は下記の2点に対して行い、定性的な確認のみに留めた。動径波動関数と球面調和関数の計算結果については以前書いた記事でまとめている(参考[4,5])。

動径波動関数が0になる位置で電子波動関数も0になっているか？
球面調和関数の形と電子波動関数の形が大まかに同じ形をしているか？

以前書いた記事に載せている球面調和関数のグラフと今回の記事で載せている電子波動関数のグラフとでカメラアングルが異なり、モニターサイズやグラフの解像度の問題で、良く見比べてみないとx軸とy軸が入れ替わっているように見えるので注意されたい。

図4. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=1,\ l=0,\ m=0$

図5. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=2,\ l=0 \sim 1,\ m=-1\sim 1$

図5-1. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=2,\ l=0,\ m=0$

図5-2. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=2,\ l=1,\ m=-1$

図5-3. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=2,\ l=1,\ m=0$

図5-4. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=2,\ l=1,\ m=1$

図6. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=3,\ l=0 \sim 2,\ m=-2\sim 2$

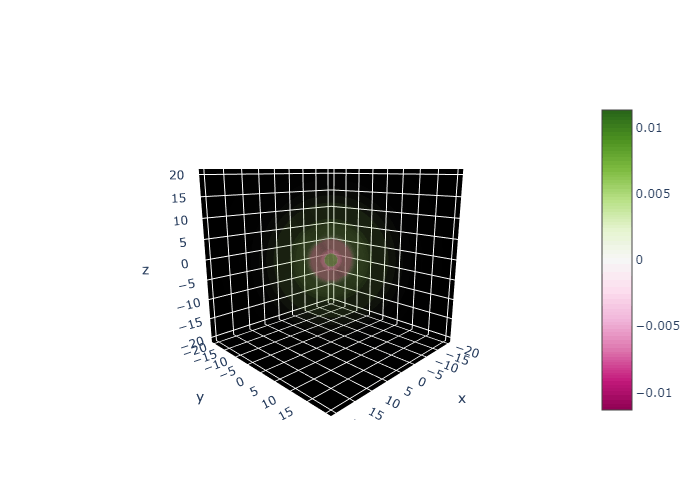
図6-1. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=3,\ l=0,\ m=0$

図6-2. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=3,\ l=1,\ m=-1$

図6-3. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=3,\ l=1,\ m=0$

図6-4. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=3,\ l=1,\ m=1$

図6-5. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=3,\ l=2,\ m=-2$

図6-6. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=3,\ l=2,\ m=-1$

図6-7. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=3,\ l=2,\ m=0$

図6-8. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=3,\ l=2,\ m=1$

図6-9. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=3,\ l=2,\ m=2$

図7. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=0 \sim 3,\ m=-3\sim 3$

図7-1. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=0,\ m=0$

図7-2. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=1,\ m=-1$

図7-3. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=1,\ m=0$

図7-4. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=1,\ m=1$

図7-5. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=2,\ m=-2$

図7-6. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=2,\ m=-1$

図7-7. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=2,\ m=0$

図7-8. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=2,\ m=1$

図7-9. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=2,\ m=2$

図7-10. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=3,\ m=-3$

図7-11. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=3,\ m=-2$

図7-12. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=3,\ m=-1$

図7-13. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=3,\ m=0$

図7-14. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=3,\ m=1$

図7-15. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=3,\ m=2$

図7-16. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=3,\ m=3$

3-3.電子波動関数(インタラクティブ描画)

ここでは、電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ をインタラクティブ描画をしてみて、その結果を確認している様子をモーションキャプチャーし、gifアニメーション化したものを示す。前節で示した図4~7の中でも静止画ではグラフが見にくいと思ったものを図8~14に示した。図15~18には、 $n=5,\ 6$ となるものの内、個人的に見てみたいと思ったグラフを描画している。

図8. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=3,\ l=1,\ m=1$

図9. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=3,\ l=2,\ m=2$

図10. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=1,\ m=-1$

図11. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=2,\ m=-2$

図12. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=2,\ m=0$

図13. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=3,\ m=2$

図14. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=4,\ l=3,\ m=3$

図15. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=5,\ l=2,\ m=-1$

図16. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=5,\ l=3,\ m=0$

図17. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=6,\ l=5,\ m=3$

図18. 実数化された電子波動関数 $\Psi_{nlm}(r,\theta,\phi)$ ： $n=6,\ l=5,\ m=5$

謝辞

今回、水素原子の可視化関連の記事(参考[4,5])を作成するにあたり、沢山の資料を参考にさせて頂きました。量子力学の基本的な考え方は参考[17]の教科書から得たものが大きく、特に水素原子の解析解の求め方は参考[18]の教科書を参考にさせて頂きました。これらの教科書の著者である桜井先生、猪木先生は残念ながら亡くなられていますが（川合先生は2022年現在ご健在です）、感謝申し上げたいと思います。大変勉強になりました。有難うございます。Web上に公開されている記事の中では参考[19]と参考[20]の記事を一番よく参照し、勉強させて頂きました。記事の製作者の方、有難うございます。また、無料の計算ライブラリを開発してくださっているコントリビュータの方にも頭が上がりません。有難うございます。この他にも参照させて頂いた教科書やWeb上の記事が沢山ありますが、最小限のものしか参考資料の欄に記載できていません。

また、解説が徒に冗長で纏まりも無く、間違った解説をしてしまっている可能性もあるため、Web上に記事として公開するのに躊躇する気持ちもありましたが、自分の勉強の過程として残しておくことにしました。久しぶりに量子力学の勉強がしたくなり、教科書に答えは載っているし簡単だろうという軽い気持ちで水素原子の解の描画に取り掛かりましたが、案外難しかったです。量子力学そのものの難しさというより、特殊関数の定義の"揺れ"やグラフ描画の技術的な面で手こずりました。

一方で、"水素原子の解を描いてみる"という初等的で具体的な問題を記事化していく事を通し、量子力学の中で自分が何を理解できていないかが浮き彫りになり、まだまだ勉強が足りないなということを再確認できました。記事中の誤りの指摘などは歓迎しますので、誤りを見つけた方はコメント欄やTwitterのメッセージ等で教えて頂けますと幸いです。

最後に、こんな長ったらしい記事を読んでくれた方にも感謝申し上げたいと思います。有難うございます。

環境

ソフト

・plotly 5.9.0
・scipy 1.7.3
・numpy 1.21.5
・python 3.9.13
・IPython 8.4.0
・Anaconda 4.14.0
・Spyder 5.9.2
・Windows 10 Home 64bit

ハード：2020年頃に5~6万円で購入したLenovoのノートPC

・製品名：IdeaPad S540-14API
・CPU：AMD Ryzen 5 3500U with Radeon Vega Mobile Gfx 2.10 GHz
・RAM：8.00 GB
・内臓GPU：AMD Radeon(TM) Vega 8 Graphics

参考