Juliaで可視化:水素原子
Juliaで可視化シリーズ第3段, 水素原子のSchrödinger方程式の解を可視化する.

 |
 |
 |
 |
 |
|
 |
 |
|
 |
||
 |
パッケージ
事前に次のパッケージモードで次の6つのパッケージをインストールする必要がある. ノート上ではusing Plots, using Printf, using LaTeXStrings, using Polynomials, using SpecialPolynomialsを宣言する. なお, Plots.jlとGR.jlは干渉することが多いので, 後で宣言する.
# using Pkg
# Pkg.add("GR")
# Pkg.add("Plots")
# Pkg.add("Printf")
# Pkg.add("LaTeXStrings")
# Pkg.add("Polynomials")
# Pkg.add("SpecialPolynomials")
# using GR
using Plots
using Printf
using LaTeXStrings
using Polynomials
using SpecialPolynomials
Schrödinger方程式
水素様原子の時間に依存しないSchrödinger方程式は
である. ただし, 電子と原子核について, それぞれの質量は
が得られる. 分離の詳細は原田(2007), 高柳(2000), 河合(2002), Jensen(2007)などを参照されたい. さらに
となる. よく知られている通り, このSchrödinger方程式に対する固有値は
である(高柳(2000)を元に一部変更). ただし,
である(高柳(2000)を元に一部変更). ただし, 上記はラゲール多項式を
V(r;Z=1) = -Z/abs(r)
E(n;Z=1) = -Z^2/(2*n^2)
function R(n,l,r;Z=1)
a0 = 1
ρ = 2*Z*abs(r)/(n*a0)
N = -sqrt( factorial(n-l-1)/(2*n*factorial(n+l)^3) * (2*Z/(n*a0))^3 )
return N*ρ^l * exp(-ρ/2) * L(n+l,2*l+1,ρ)
end
function Y(l,m,θ,φ)
N = (im)^(m+abs(m)) * sqrt( (2*l+1)*factorial(l-Int(abs(m))) / (2*factorial(l+Int(abs(m)))) )
return N * P(l,Int(abs(m)),cos(θ)) * exp(im*m*φ) / sqrt(2*π)
end
# ψ(n,l,m,r,θ,φ) = R(n,l,r)*Y(m,l,θ,φ)
ψ(n,l,m,x,y,z) = R(n,l,r(x,y,z))*Y(l,m,θ(x,y,z),φ(x,y,z))
補足
いくつかの関数が必要になるので, 補足しておく.
動径関数についての注意点
日本語・英語圏, 数学者・物理学者, 新旧の違いなどによって採用される定義に偏りがあるようで, ライブラリの実装にも関係してくるため, この件については把握しておいた方がよい. まず表を示すと, 動径関数
| パターン | ラゲール多項式 |
|
規格化因子の分母 | 文献 |
|---|---|---|---|---|
| 1 | ||||
| 2 | 1, 2 | |||
| 3 | 多数 | |||
| 4 |
まず第一にラゲール多項式
パターン3が多く, 『マッカーリ・サイモン物理化学 上』p.224, 『アトキンス 物理化学(上)第10版』p.381, 原田義也『量子化学 上巻』(第2版, 2019, 裳華房)p.123, 高柳和夫『原子分子物理学』(2000, 朝倉書店)p.16, 国広悌二『基幹講座物理学 量子力学』(東京図書, 2018)p.125, Wikipedia(日本語)などがこれに該当する.
しかし, SpecialPolynomials.jlで最も自然な実装になるのはパターン2である. そもそもラゲール多項式
| 多項式 | 満たすべき方程式 | 参考 |
|---|---|---|
| ラゲール多項式 |
||
| ラゲールの陪多項式 |
日本語のWikipedia | |
| Generalized Laguerre polynomials 一般化ラゲール多項式 |
英語のWikipedia |
上表のように, ラゲール多項式
ラゲールの陪多項式L_n^k(x)
ラゲールの陪多項式
という関係を利用してラゲールの陪多項式を生成する. また, SpecialPolynomials.jlはそもそものラゲール多項式
であるので, 最初に説明した動径関数で利用するためには
の定義になるように調整する必要がある.
# ただしラゲール多項式L_n(x)が1/n!を含まない場合
# using SpecialPolynomials
L(n,k,x) = factorial(n) * basis(Laguerre{k}, n-k)(x)
球面調和関数についての注意点
ルジャンドルの陪多項式
| 位相因子 | 文献 |
|---|---|
| 高柳和夫『原子分子物理学』(2000, 朝倉書店) p.16, |
|
| 多数派?上村洸『基礎からの量子力学』(裳華房, 2016), Wikipedia | |
| こちらのページ, 猪木・川合, 上記と同じ? | |
| 国広悌二『量子力学』(東京図書, 2018), Wikipedia - 球面調和関数(英語版) |
※ ランダウ=リフシッツは付録に球面調和関数の具体的な表式があるが, 複素数が含まれているので, 一致する.
※
など多数ある. けっこう頑張ったと思うので, その他の生態系の調査は読者に任せる. もし自分が使うときになったら慎重に性質を確認する必要があるということだけはおわかりいただけただろうか.
ルジャンドルの陪多項式P_k^m(t)
ルジャンドルの陪多項式
# using SpecialPolynomials
# using Polynomials
function P(k,m)
#if m<0
# return (-1)^m * factorial(l-m) / factorial(l+m) * P(k,m,x)
#end
p = basis(Legendre, k)
q = convert(Polynomial, p)
r = derivative(q, m)
return x -> (1-x^2)^(m/2) * r(x)
end
LegendreArray = Dict()
for k in 0:7 # 今回はk=7までを予めメモリに格納しておく.
for m in 0:k
LegendreArray[k,m] = P(k,m)
end
end
P(k,m,x) = LegendreArray[k,m](x)
球面座標
直交座標と球面座標の変換はWikipediaに書いてある通り
であるが, 実装してみると問題に気付く. まず,
x(r,θ,φ) = r*sin(θ)*cos(φ)
y(r,θ,φ) = r*sin(θ)*sin(φ)
z(r,θ,φ) = r*cos(θ)
r(x,y,z) = sqrt(x^2+y^2+z^2)
θ(x,y,z) = x^2+y^2<1e-9 ? 0.0 : myacos(z/r(x,y,z))
φ(x,y,z) = y^2<1e-9 ? 0.0 : sign(y)*myacos(x/sqrt(x^2+y^2))
# θ(x,y,z) = acos(z/r(x,y,z))
# φ(x,y,z) = sign(y)*acos(x/sqrt(x^2+y^2))
上記のmyacos(x)はacos(x)に対して周期性を持たせた関数である.
loop(x) = x<-1 ? loop(x+2) : (1<x ? loop(x-2) : x)
myacos(x) = acos(loop(x))
# テスト
println("x\tloop(x)\tacos(x)\tmyacos(x)")
for x in -3:0.2:3
@printf("%.2f\t%.2f\t%.2f\t%.2f\n", x, loop(x), (try; acos(x); catch; NaN; end), myacos(x) )
end
x loop(x) acos(x) myacos(x)
-3.00 -1.00 NaN 3.14
-2.80 -0.80 NaN 2.50
-2.60 -0.60 NaN 2.21
-2.40 -0.40 NaN 1.98
-2.20 -0.20 NaN 1.77
-2.00 0.00 NaN 1.57
-1.80 0.20 NaN 1.37
-1.60 0.40 NaN 1.16
-1.40 0.60 NaN 0.93
-1.20 0.80 NaN 0.64
-1.00 -1.00 3.14 3.14
-0.80 -0.80 2.50 2.50
-0.60 -0.60 2.21 2.21
-0.40 -0.40 1.98 1.98
-0.20 -0.20 1.77 1.77
0.00 0.00 1.57 1.57
0.20 0.20 1.37 1.37
0.40 0.40 1.16 1.16
0.60 0.60 0.93 0.93
0.80 0.80 0.64 0.64
1.00 1.00 0.00 0.00
1.20 -0.80 NaN 2.50
1.40 -0.60 NaN 2.21
1.60 -0.40 NaN 1.98
1.80 -0.20 NaN 1.77
2.00 0.00 NaN 1.57
2.20 0.20 NaN 1.37
2.40 0.40 NaN 1.16
2.60 0.60 NaN 0.93
2.80 0.80 NaN 0.64
3.00 1.00 NaN 0.00
軌道の名前
最後に, 量子数と軌道の名前を対応させる関数を作ったが, これが意外と便利だった.
# 軌道の名前
orbital_name(n,l) = "$n$(["s","p","d","f","g","h"][l+1])"
期待値の確認
各種の期待値を計算するため, 簡単な数値積分のルーチンを用意し, ガウス積分を計算してテストを行った.
integral(func, x_min, x_max, dx) = sum(func.(x_min:dx:x_max))*dx
# テスト(ガウス積分)
integral(x->exp(-x^2)/sqrt(pi), -10,10,0.1) |> display
1.0
function integral2D(func, x_min, x_max, dx, y_min, y_max, dy)
sum = 0.0
for x in x_min:dx:x_max
for y in y_min:dy:y_max
sum += func(x,y)*dx*dy
end
end
return sum
end
# テスト(ガウス積分)
integral2D((x,y)->exp(-x^2-y^2)/sqrt(pi^2), -10,10,0.1, -10,10,0.1) |> display
0.9999999999999957
規格化条件
固有関数が正しく宣言できているのか見た目だけでは判断できないことが多いので, ライブラリの使い方が正しいか, バグが無いか, 文献に誤りがないか等を確認する意味も含め, まず最初に規格化条件を満足するか簡単に計算する. 数値積分なので完全に1にはならないが, 概ね1なら問題ない.
動径部分について次式が成り立つはずである.
println("\t∫r^2R^2(r)dr")
for n in 1:5
for l in 0:n-1
@printf("%s\t%.17f\n", orbital_name(n,l), integral(r->r^2*abs(R(n,l,r))^2, 0, 100, 0.01))
end
end
∫r^2R^2(r)dr
1s 0.99999999933335459
2s 0.99999999991666833
2p 0.99999999999999989
3s 0.99999999997530897
3p 1.00000000000000000
3d 1.00000000000000000
4s 0.99999999998488820
4p 0.99999999999693834
4d 0.99999999999879452
4f 0.99999999999977918
5s 0.99999930806578163
5p 0.99999948583752063
5d 0.99999972631969702
5f 0.99999990537286676
5g 0.99999998382258726
角度部分について次式が成り立つはずである.
println("l\tm\t∫|Y(θ,φ)|^2sinθdθdφ")
for l in 1:3
for m in -l:l
@printf("%d\t%d\t%.17f\n", l, m, integral2D((θ,φ)->abs(Y(l,m,θ,φ))^2*sin(θ), 0,π,0.01, 0,2*π,0.01))
end
end
l m ∫|Y(θ,φ)|^2sinθdθdφ
1 -1 1.00108459213941758
1 0 1.00106961810439521
1 1 1.00108459213941758
2 -2 1.00108459204766698
2 -1 1.00108459250535242
2 0 1.00105963486609806
2 1 1.00108459250535242
2 2 1.00108459204766698
3 -3 1.00108459204825762
3 -2 1.00108459204782041
3 -1 1.00108459332884259
3 0 1.00104965071179763
3 1 1.00108459332884259
3 2 1.00108459204782041
3 3 1.00108459204825762
わりと誤差が大きい点が気になるが, 恐らく積分領域の末端の記述がかなり悪いせいであると思われる. 次に確認する通り, 一応は規格直交性も満足しているようなので今回はよしとする.
直交性
規格化条件のついでに直交性も確認しておく.
println("l\tl'\t∫Y*(θ,φ)Y(θ,φ)sinθdθdφ")
m = 0
for l in 1:4
for ll in 1:4
@printf("%d\t%d\t%.17f\n", l, ll, integral2D((θ,φ)->conj(Y(l,m,θ,φ))*Y(ll,m,θ,φ)*sin(θ), 0,π,0.01, 0,2*π,0.01))
end
end
l l' ∫Y*(θ,φ)Y(θ,φ)sinθdθdφ
1 1 1.00106961810439521
1 2 -0.00001297905216095
1 3 -0.00002287377512273
1 4 -0.00001741363401505
2 1 -0.00001297905216095
2 2 1.00105963486609806
2 3 -0.00001982616166688
2 4 -0.00003348500577979
3 1 -0.00002287377512273
3 2 -0.00001982616166688
3 3 1.00104965071179763
3 4 -0.00002660021073039
4 1 -0.00001741363401505
4 2 -0.00003348500577979
4 3 -0.00002660021073039
4 4 1.00103966527685562
ビリアル定理
クーロンポテンシャルでは
println("\tE\t\t\t<V>/2")
for n in 1:5
for l in 0:n-1
@printf("%s\t%.17f\t%.17f\n", orbital_name(n,l), E(n), integral(r->V(r)*r^2*abs(R(n,l,r))^2, 0.01, 100, 0.01)/2)
end
end
E <V>/2
1s -0.50000000000000000 -0.49998333366666148
2s -0.12500000000000000 -0.12499791670312468
2p -0.12500000000000000 -0.12500000000173608
3s -0.05555555555555555 -0.05555493828212155
3p -0.05555555555555555 -0.05555555555616521
3d -0.05555555555555555 -0.05555555555555557
4s -0.03125000000000000 -0.03124973958770489
4p -0.03125000000000000 -0.03125000000025629
4d -0.03125000000000000 -0.03124999999999411
4f -0.03125000000000000 -0.03124999999999892
5s -0.02000000000000000 -0.01999986331948914
5p -0.02000000000000000 -0.01999999751095307
5d -0.02000000000000000 -0.01999999867474622
5f -0.02000000000000000 -0.01999999954163147
5g -0.02000000000000000 -0.01999999992160406
期待値\langle r\rangle
いろいろな期待値がこちらのサイトや高柳(2000)p.20などで紹介されている.
r(n,l;Z=1) = (3*n^2-l*(l+1))/2
println("\texact\t\t\t<r>")
for n in 1:6
for l in 0:n-1
@printf("%s\t%2.17f\t%2.17f\n", orbital_name(n,l), r(n,l), integral(r->r^3*abs(R(n,l,r))^2, 0.1, 1000, 0.01))
end
end
exact <r>
1s 1.50000000000000000 1.49993035023037469
2s 6.00000000000000000 5.99999130697251903
2p 5.00000000000000000 4.99999999535692119
3s 13.50000000000000000 13.49999742501150735
3p 12.50000000000000000 12.49999999836981246
3d 10.50000000000000000 10.49999999999993605
4s 24.00000000000000000 23.99999891378351080
4p 23.00000000000000000 22.99999999927470284
4d 21.00000000000000000 20.99999999999996803
4f 18.00000000000000000 18.00000000000000355
5s 37.50000000000000000 37.49999944388246575
5p 36.50000000000000000 36.49999999961975305
5d 34.50000000000000000 34.49999999999998579
5f 31.50000000000000000 31.50000000000001066
5g 27.50000000000000000 27.50000000000000000
6s 54.00000000000000000 53.99999967818066438
6p 53.00000000000000000 52.99999999977713117
6d 51.00000000000000000 50.99999999999999289
6f 48.00000000000000000 48.00000000000000711
6g 44.00000000000000000 16094.43124042773706606
6h 39.00000000000000000 14506950.32743391394615173
可視化
エネルギー固有値
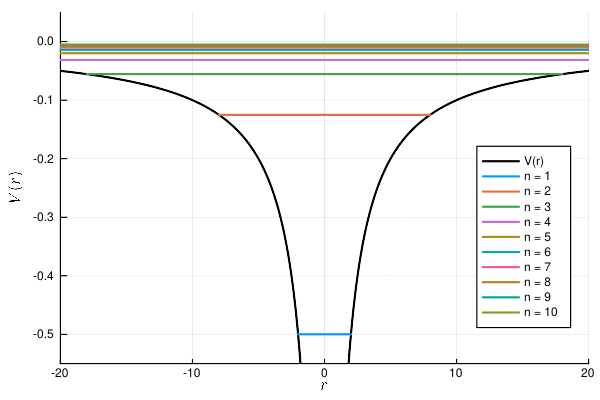
まず, ポテンシャルと固有値を図示する.
# using Plots
plot(xlabel="\$r\$", ylabel="\$V(r)\$", xlims=(-20,20), ylims=(-0.55,0.05), legend=:bottomright) #, xticks=-15:1:15)
plot!(-50:0.1:50, r->V(r), label="V(r)", lc="#000000", lw=2)
for n in 1:10
plot!([1/E(n), -1/E(n)], fill(E(n),2), lc=n, lw=2, label="n = $n")
end
plot!()
スペクトル系列
エネルギー固有値の差からスペクトルを導出でき, 実験と直接的に比較できる. こちらを確認されたい.
# https://physics.nist.gov/cgi-bin/cuu/CCValue?hrminv
Eh2m1 = 2.1947463136320*1e7
Eh2cm1 = 2.1947463136320*1e5
Eh2nm1 = 2.1947463136320*1e-2
frequency(n,m;Z=1) = (E(n,Z=Z) - E(m,Z=Z))*Eh2cm1
wavelength(n,m;Z=1) = 1/((E(n,Z=Z) - E(m,Z=Z))*Eh2nm1)
println("\tLymann\t\tBalmer\t\tPaschen")
println("n -> m\tm=1\t\tm=2\t\tm=3")
@printf("n = %-3d\t%.2f\tnm\n", 2, wavelength(2,1))
@printf("n = %-3d\t%.2f\tnm\t%.2f\tnm\n", 3, wavelength(3,1), wavelength(3,2))
for i in [4,5,6,7,8,9,10,Inf]
@printf("n = %-3d\t%.2f\tnm\t%.2f\tnm\t%.2f\tnm\n", i, wavelength(i,1), wavelength(i,2), wavelength(i,3))
end
Lymann Balmer Paschen
n -> m m=1 m=2 m=3
n = 2 121.50 nm
n = 3 102.52 nm 656.11 nm
n = 4 97.20 nm 486.01 nm 1874.61 nm
n = 5 94.92 nm 433.94 nm 1281.47 nm
n = 6 93.73 nm 410.07 nm 1093.52 nm
n = 7 93.03 nm 396.91 nm 1004.67 nm
n = 8 92.57 nm 388.81 nm 954.35 nm
n = 9 92.27 nm 383.44 nm 922.66 nm
n = 10 92.05 nm 379.69 nm 901.25 nm
n = Inf 91.13 nm 364.51 nm 820.14 nm
# using Plots
Plots.plot(size=(800, 150), yshowaxis=false, grid=false, xscale=:log10, ylims=(0,3))
xticks!([100,1000,10000], ["100nm", "1000nm", "10000nm"])
for j in 1:6
plot!(annotations=(wavelength(j+1,j), 2.9, (["Lyman", "Balmer ", "Paschen ", "Brackett ", "Pfund ", "Humphreys "][j], 8, 0.0, :right)))
plot!(annotations=(wavelength(j+1,j), 2.5, (@sprintf("~%.2f", wavelength(j+1,j)), 8, 0.0, :right)))
for i in j+1:15
if i==j+1
plot!(fill(wavelength(i,j),2), [0,2.3], label="", lc=j)
else
plot!(fill(wavelength(i,j),2), [0,2], label="", lc=j)
end
end
end
plot!()

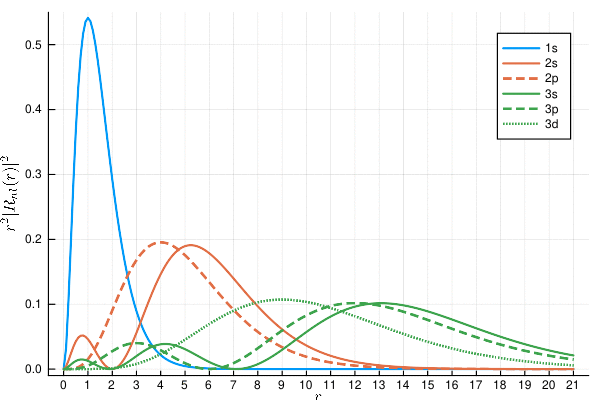
動径関数
動径密度関数を描写した. こちらのページまたはWikipedia等と見比べて, 節や腹の位置を確認して頂きたい.
# using Plots
plot(xlabel="\$r\$", ylabel="\$r^2|R_{nl}(r)|^2\$", ylims=(-0.01,0.55), xticks=0:1:21)
for n in 1:3
for l in 0:n-1
plot!(0:0.1:21, r->r^2*R(n,l,r)^2, label=orbital_name(n,l), lc=n, lw=2, ls=[:solid,:dash,:dot,:dashdot,:dashdotdot][l+1])
end
end
plot!()

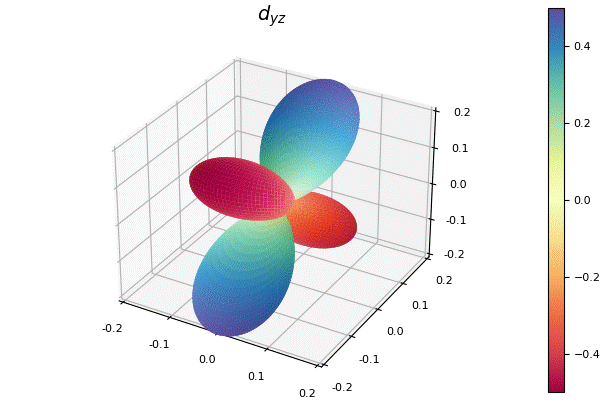
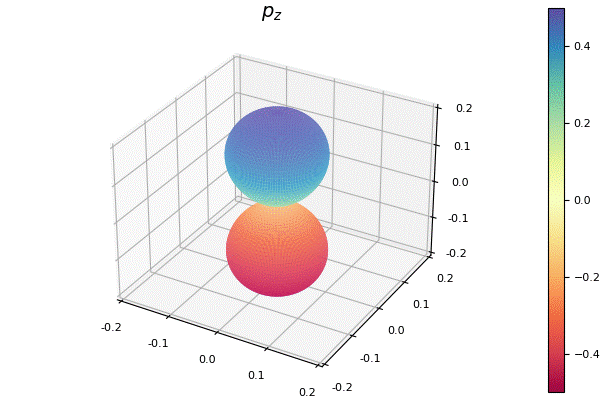
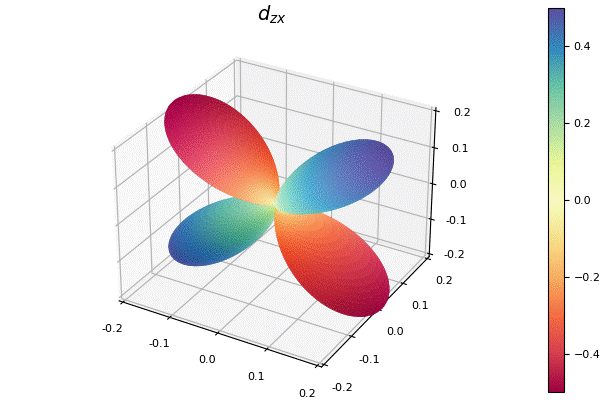
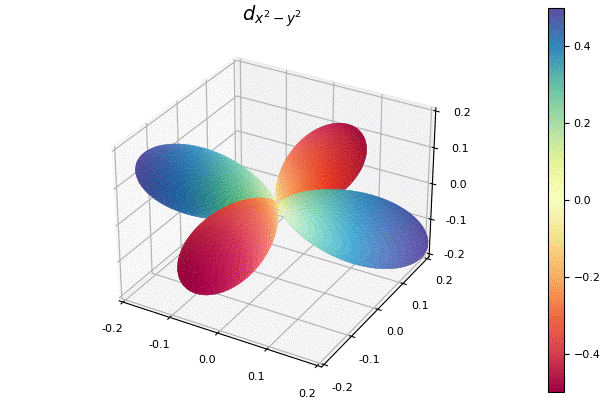
球面調和関数
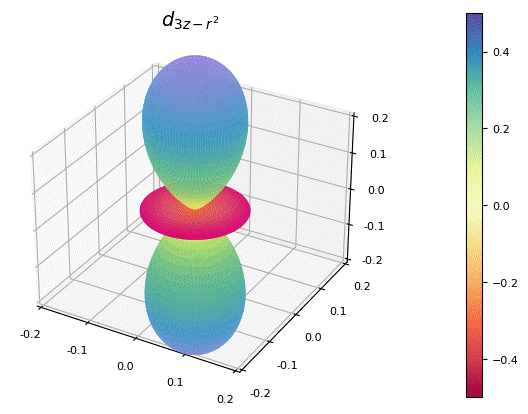
球面調和関数は複素数値であるので, よく目にするfill_z=Cを指定した.
pyplot()
function my_surface(N, M, f; xlims=(-0.2,0.2), ylims=(-0.2,0.2), zlims=(-0.2,0.2), clims=(-0.5,0.5), title="")
Θ = range(0, stop=π, length=N)
Φ = range(0, stop=2*π, length=M)
p(θ,φ) = abs(f(θ,φ))^2
X = zeros(N, M)
Y = zeros(N, M)
Z = zeros(N, M)
C = zeros(N, M)
for j in 1:M
for i in 1:N
X[i,j] = p(Θ[i],Φ[j]) * sin(Θ[i])*cos(Φ[j])
Y[i,j] = p(Θ[i],Φ[j]) * sin(Θ[i])*sin(Φ[j])
Z[i,j] = p(Θ[i],Φ[j]) * cos(Θ[i])
C[i,j] = real(f(Θ[i],Φ[j]))
end
end
plt = surface(X, Y, Z, fill_z=C, xlims=xlims, ylims=ylims, zlims=zlims, clims=clims, title=title, c=:Spectral)
plot(plt) |> display
return plt
end
f(θ,φ) = Y(0,0,θ,φ)
my_surface(100, 200, f, title=L"1s")
f(θ,φ) = (Y(1,-1,θ,φ) - Y(1,1,θ,φ)) / sqrt(2)
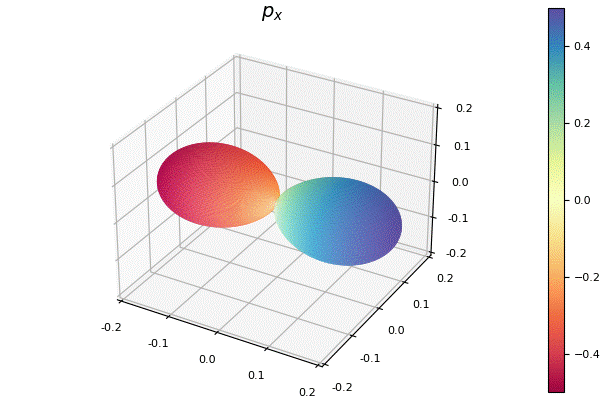
my_surface(100, 200, f, title=L"2p_x")
f(θ,φ) = (Y(1,-1,θ,φ) + Y(1,1,θ,φ)) * im / sqrt(2)
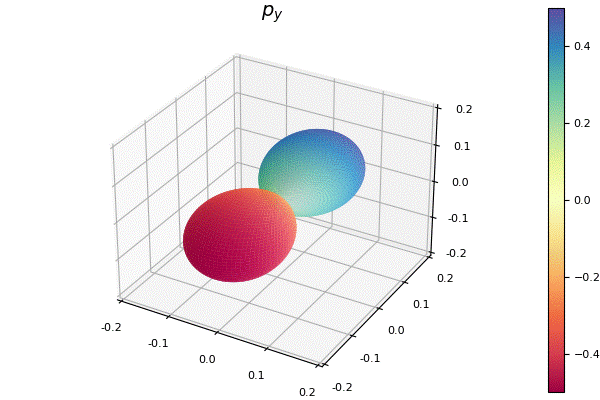
my_surface(100, 200, f, title=L"2p_y")
f(θ,φ) = Y(1,0,θ,φ)
my_surface(100, 200, f, title=L"2p_z")
f(θ,φ) = (Y(2,-2,θ,φ) - Y(2,2,θ,φ)) * im / sqrt(2)
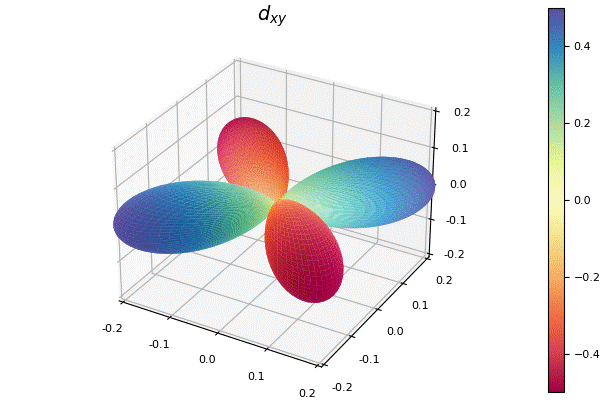
my_surface(100, 200, f, title=L"d_{xy}")
f(θ,φ) = (Y(2,-1,θ,φ) + Y(2,1,θ,φ)) * im / sqrt(2)
my_surface(100, 200, f, title=L"d_{yz}")
f(θ,φ) = (Y(2,-1,θ,φ) - Y(2,1,θ,φ)) / sqrt(2)
my_surface(100, 200, f, title=L"d_{zx}")
f(θ,φ) = (Y(2,-2,θ,φ) + Y(2,2,θ,φ)) / sqrt(2)
my_surface(100, 200, f, title=L"d_{x^2-y^2}")
f(θ,φ) = Y(2,0,θ,φ)
my_surface(100, 200, f, title=L"d_{3z-r^2}")









軌道の可視化
上記の球面調和関数の図は飽くまでも角度A[:,:,:]から等値面を描写する. Plots.jlとGR.jlは干渉することが多いので, モジュールの中でusing GRを宣言する方がよい.
module Orbital
using GR
GR.__init__()
function isosurface(x_min, x_max, dx, func; isovalue=NaN, rotation=180 , tilt=150)
s = x_min:dx:x_max # 3軸方向に共通してx_min≦x≦x_x_mmaxの点をdx刻みでサンプリングする
N = length(s)
array = zeros(N,N,N)
for k in 1:N
for j in 1:N
for i in 1:N
array[i,j,k] = func(s[i],s[j],s[k])
end
end
end
if isnan(isovalue) || isovalue<minimum(array) || maximum(array)<isovalue
isovalue = sum(array)/length(array)
end
GR.isosurface(array, isovalue=isovalue, rotation=rotation , tilt=tilt) |> display
end
end
# # テスト(d型ガウス軌道の描写)
# f(x,y,z) = (x*y*exp(-(x^2+y^2+z^2)))^2
# Orbital.isosurface(-2, 2, 0.1, f)
L"1s" |> display
f(x,y,z) = abs(ψ(1,0,0,x,y,z))^2
Orbital.isosurface(-10, 10, 0.5, f)
L"2p_x" |> display
f(x,y,z) = abs(ψ(2,1,1,x,y,z) + ψ(2,1,-1,x,y,z))^2 / 2
Orbital.isosurface(-10, 10, 0.5, f)
L"2p_y" |> display
f(x,y,z) = abs(ψ(2,1,1,x,y,z) - ψ(2,1,-1,x,y,z))^2 / 2
Orbital.isosurface(-10, 10, 0.5, f)
L"2p_z" |> display
f(x,y,z) = abs(ψ(2,1,0,x,y,z))^2
Orbital.isosurface(-10, 10, 0.5, f)
L"3d_{xy}" |> display
f(x,y,z) = abs(ψ(3,2,-2,x,y,z) - ψ(3,2,2,x,y,z))^2 / 2
Orbital.isosurface(-20, 20, 1.0, f)
L"3d_{yz}" |> display
f(x,y,z) = abs(ψ(3,2,-1,x,y,z) + ψ(3,2,1,x,y,z))^2 / 2
Orbital.isosurface(-20, 20, 1.0, f)
L"3d_{zx}" |> display
f(x,y,z) = abs(ψ(3,2,-1,x,y,z) - ψ(3,2,1,x,y,z))^2 / 2
Orbital.isosurface(-20, 20, 1.0, f)
L"3d_{x^2-y^2}" |> display
f(x,y,z) = abs(ψ(3,2,-2,x,y,z) + ψ(3,2,2,x,y,z))^2 / 2
Orbital.isosurface(-20, 20, 1.0, f)
L"3d_{3z^2-r^2}" |> display
f(x,y,z) = abs(ψ(3,2,0,x,y,z))^2
Orbital.isosurface(-20, 20, 1.0, f)
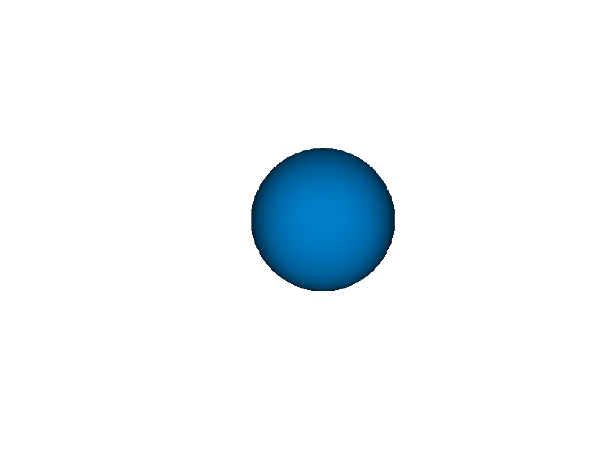


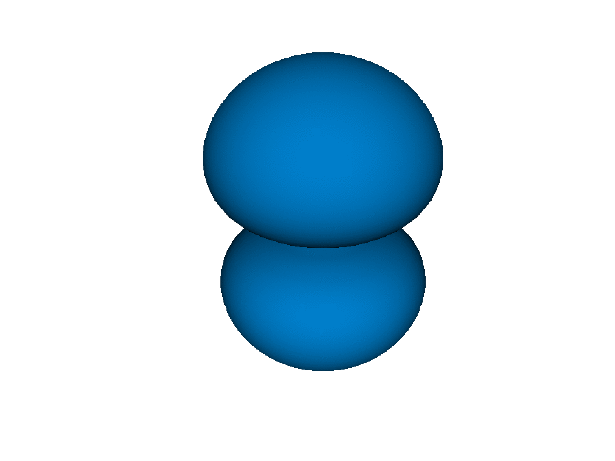
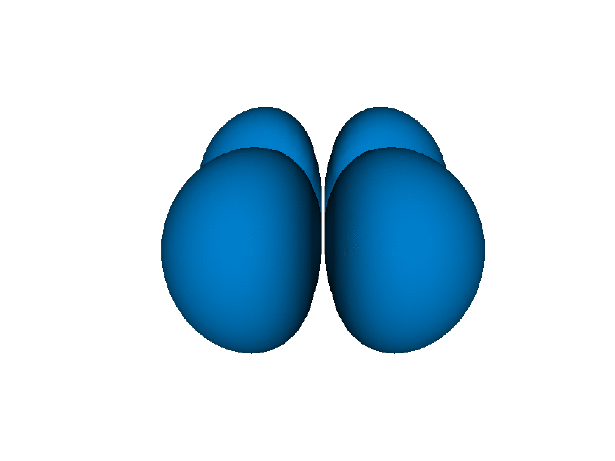
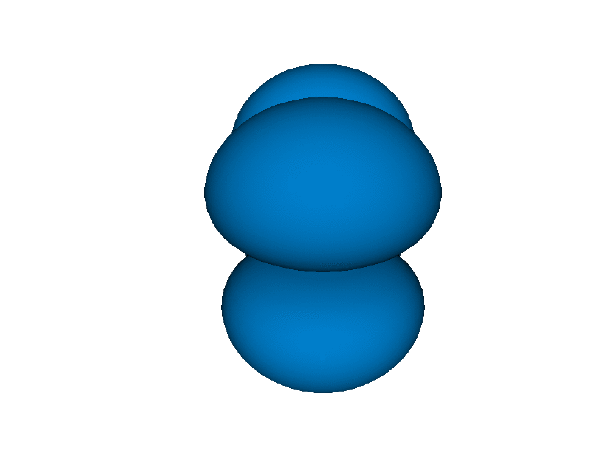
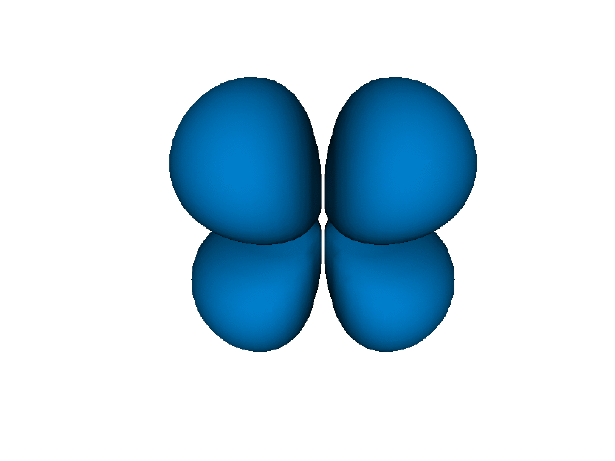
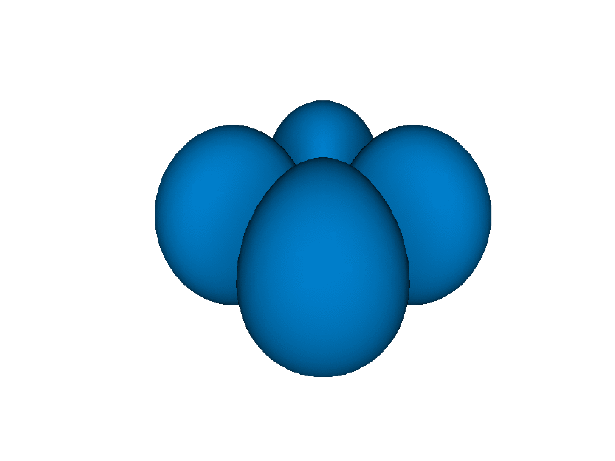
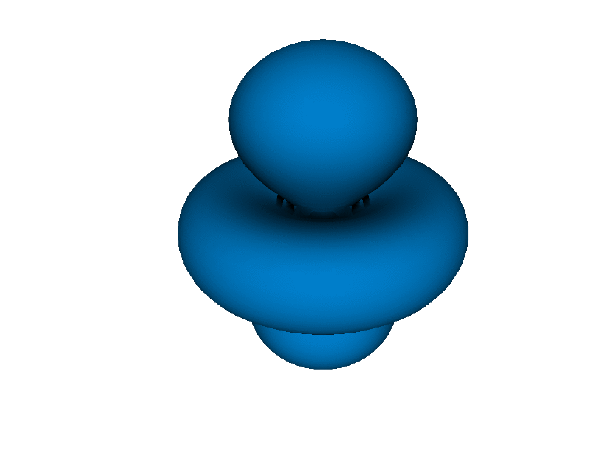
もちろん2sや3sもあるが, 断面を見たり透明度を表現できるライブラリでないと差がわからないので省略した.
おわりに
特殊関数を取り巻く複雑な事情を垣間見た. 先人の定義に従いたい物理学者と, より一般化した概念に置き換えたい数学者のせめぎ合いという構図もあるのだろう. Juliaでの特殊関数の使い方については別の記事でまとめることにする.
水素原子という最も簡単な原子・分子でさえ, 等値面の描写にここまで苦労するとは思わなかった. 等値面を気軽に描けるライブラリを開発すれば, 計算物理・計算化学でのJuliaの利用が進みそうだ.
動作環境
versioninfo()
Julia Version 1.6.2
Commit 1b93d53fc4 (2021-07-14 15:36 UTC)
Platform Info:
OS: Windows (x86_64-w64-mingw32)
CPU: Intel(R) Core(TM) i7-4650U CPU @ 1.70GHz
WORD_SIZE: 64
LIBM: libopenlibm
LLVM: libLLVM-11.0.1 (ORCJIT, haswell)
参考文献
- 原田義也『量子化学 下巻』(裳華房, 2007) §A2.3
- 高柳和夫『朝倉物理学大系 11 原子分子物理学』(2000, 朝倉書店) pp.11-22
- 河合光路, 吉田思郎『朝倉物理学大系 19 原子核反応論』(朝倉書店, 2002) pp.8-12,25-38
- Frank Jensen『Introduction to Computational Chemistry, 2nd Edition』(John Wiley & Sons, 2007) pp.14-17
- IUPAC GreenBook 3.9.2
- Juliaで特殊関数を使う
- 伊藤弘毅『球面調和関数』(2005)
- @Hinamoooon『Julia: Plotsのsurface plotに行列の色をマップする』(2021)
- 若松寛『量子化学ノート』(2007)より動径分布関数
この記事の元になったJupyter Notebookのデータは下記のリンクにある.
Juliaで可視化シリーズ
Discussion