Zenn
🎸

Juliaで可視化：非調和振動子

2022/01/07に公開
Julia
量子力学
可視化
物理
グラフ
tech

モースポテンシャルの中を運動する粒子のSchrödinger方程式の解を可視化する.

パッケージ

Juliaのパッケージモードでadd Plots, add LaTeXStrings, add SpecialPolynomials, add SpecialFunctionsを実行し, 事前にパッケージをインストールしておく必要がある. また, ノート上ではusing Plots, using LaTeXStrings, using SpecialPolynomials, using Functionsを宣言する. Jupyter Notebookのインストール・使い方についてはこちらの記事, Plots.jlの使い方についてはこちらの記事を参照されたい.

パッケージ
# using Pkg
# Pkg.add("Plots")
# Pkg.add("LaTeXStrings")
# Pkg.add("SpecialPolynomials")
# Pkg.add("SpecialFunctions")
using Plots
using LaTeXStrings
using SpecialPolynomials
using SpecialFunctions

時間に依存しないSchrödinger方程式

モースポテンシャル

Morse(1929)より式(4)の記号を少し変えたモースポテンシャルは

V(r) = D_\mathrm{e} \left( \mathrm{e}^{-2a(r-r_e)} - 2\mathrm{e}^{-a(r-r_e)} \right)

であり, この中で運動する質量\muの粒子のハミルトニアンは

\hat{H} = - \frac{\hbar^2}{2\mu} \frac{\mathrm{d}^2}{\mathrm{d}r ^2} + V(r)

である. これに対する時間に依存しないSchrödinger方程式

\hat{H}\psi(r) = E \psi(r)

の解は戸田(1999)とWikipediaをそれぞれ修正して

\psi_n(\xi) = N_n z^{\lambda-n-1/2} \mathrm{e}^{-z/2} L_n^{(2\lambda-2n-1)}(\xi)\\ E_n = -D_\mathrm{e} + \hbar \omega \left( n + \frac{1}{2} \right) - \chi \hbar \omega \left( n + \frac{1}{2} \right)^2

と与えらえる. ただし, \xi=2\lambda\mathrm{e}^{-a(r-r_e)}, \omega=\sqrt{k/µ}, k=2D_\mathrm{e}a^2, \lambda=\frac{\sqrt{2mD_\mathrm{e}}}{a\hbar}, \chi=\frac{\hbar\omega}{4D_\mathrm{e}}, N_n=\sqrt{\frac{n!(2\lambda-2n-1)a}{\Gamma(2\lambda-n)}}であり, L_n^{(\alpha)}は一般化ラゲール多項式である. ラゲールの陪多項式ではないので注意されたい（詳細はこちら）. また, Wikipediaでは規格化定数N_nにaが足りないと思われるので書き加えた.

ポテンシャル
V(r, re, De, a) = De*( exp(-2*a*(r-re)) -2*exp(-a*(r-re)) )
固有関数
# using SpecialFunctions
# using SpecialPolynomials
Γ(z) = try; gamma(z); catch; Inf; end

function ψ(n, r, re ,De, a, µ)
    ℏ  = 1.0
    λ = sqrt(2*µ*De)/(a*ℏ)
    ξ = 2*λ*exp(-a*(r-re))                                    
    s  = 2*λ-2*n-1
    N  = sqrt(factorial(n)s*a/Γ(s+n+1))
    return N*ξ^(s/2)*exp(-ξ/2)*basis(Laguerre{s}, n)(ξ)
end
固有値
function E(n, De, a, µ)
    ℏ = 1.0
    k = 2*a^2*De
    ω = sqrt(k/µ)
    χ = ℏ*ω/(4*De)
    return - De + ℏ*ω*(n+1/2) - χ*ℏ*ω*(n+1/2)^2
end
パラメータ
re = 1.38436
De = 1.13133356259 - 1
k = 12.772/15.569141/2
a = sqrt(k/(2*De))
µ = 1/(1/1837.108542 + 1/1837.108542)

println("re = ", re)
println("De = ", De)
println("k  = ", k)
println("a  = ", a)
println("µ  = ", µ)
出力
re = 1.38436
De = 0.13133356259000006
k  = 0.4101703491541377
a  = 1.249623750214457
µ  = 918.554271

以上の関数とパラメータを用いて, モースポテンシャルは以下のように描写できる. V(\infty)=0 に漸近することがわかる.

# 軸ラベル, 描写範囲, 凡例位置
plot(xlabel=L"r", ylabel=L"V(r)", xlims=(0.2,6.2), ylims=(-0.14,0.01), legend=:bottomright)#, size=(450,400))

# ポテンシャル
plot!(-3:0.02:7, r->V(r,re,De,a), label="", lc="#578FC7", lw=2)

# 表示
plot!() |> display

モースポテンシャルでは有限の束縛状態でない準位ではE_{n+1} - E_{n} > 0が破綻する. これを列挙すると, n=0\sim 11までの束縛状態を持つことがわかる.

for n in 0:15
    println(n, "\t", E(n+1,De,a,µ)-E(n,De,a,µ) > 0)
end

0	true
1	true
2	true
3	true
4	true
5	true
6	true
7	true
8	true
9	true
10	true
11	true
12	false
13	false
14	false
15	false

束縛状態のエネルギー準位を全て描写すると

# 軸ラベル, 描写範囲, 凡例位置
plot(xlabel=L"r", ylabel=L"V(r)", xlims=(0.2,6.2), ylims=(-0.14,0.01), legend=:bottomright)#, size=(450,400))

# ポテンシャル
plot!(0:0.02:7, r->V(r,re,De,a), label="", lc="#578FC7", lw=2)

# エネルギー
for n in 11:-1:0
    plot!(0:0.02:7, r-> E(n,De,a,µ)<V(r,re,De,a) ? NaN : E(n,De,a,µ), label="", lc="#578FC7", lw=1)
end

# 表示
plot!() |> display

波動関数をエネルギーの高さまでシフトし, 縦に縮めて書き足す. ここでは0.004\psi(x)+E_nを描写した. 量子数nは節の数と対応していることがわかる.

# 軸ラベル, 描写範囲, 凡例位置
plot(xlabel=L"r", ylabel=L"V(r)", xlims=(0.2,6.2), ylims=(-0.14,0.01), legend=:bottomright)#, size=(450,400))

# ポテンシャル
plot!(-3:0.02:7, r->V(r,re,De,a), label="", lc="#000000", lw=2)

for n in 11:-1:0
    # エネルギー（破線）
    hline!([E(n,De,a,µ)], label="", lc="#000000", ls=:dash)
    # エネルギー（実線）
    plot!(0:0.02:7, r-> E(n,De,a,µ)<V(r,re,De,a) ? NaN : E(n,De,a,µ), label="", lc="#000000", lw=2)
    # 波動関数
    plot!(0:0.02:7, r->0.004*ψ(n,r,re,De,a,µ)+E(n,De,a,µ), label=latexstring("n=$n"), lc=n+1, lw=2)
end

# 表示
plot!() |> display

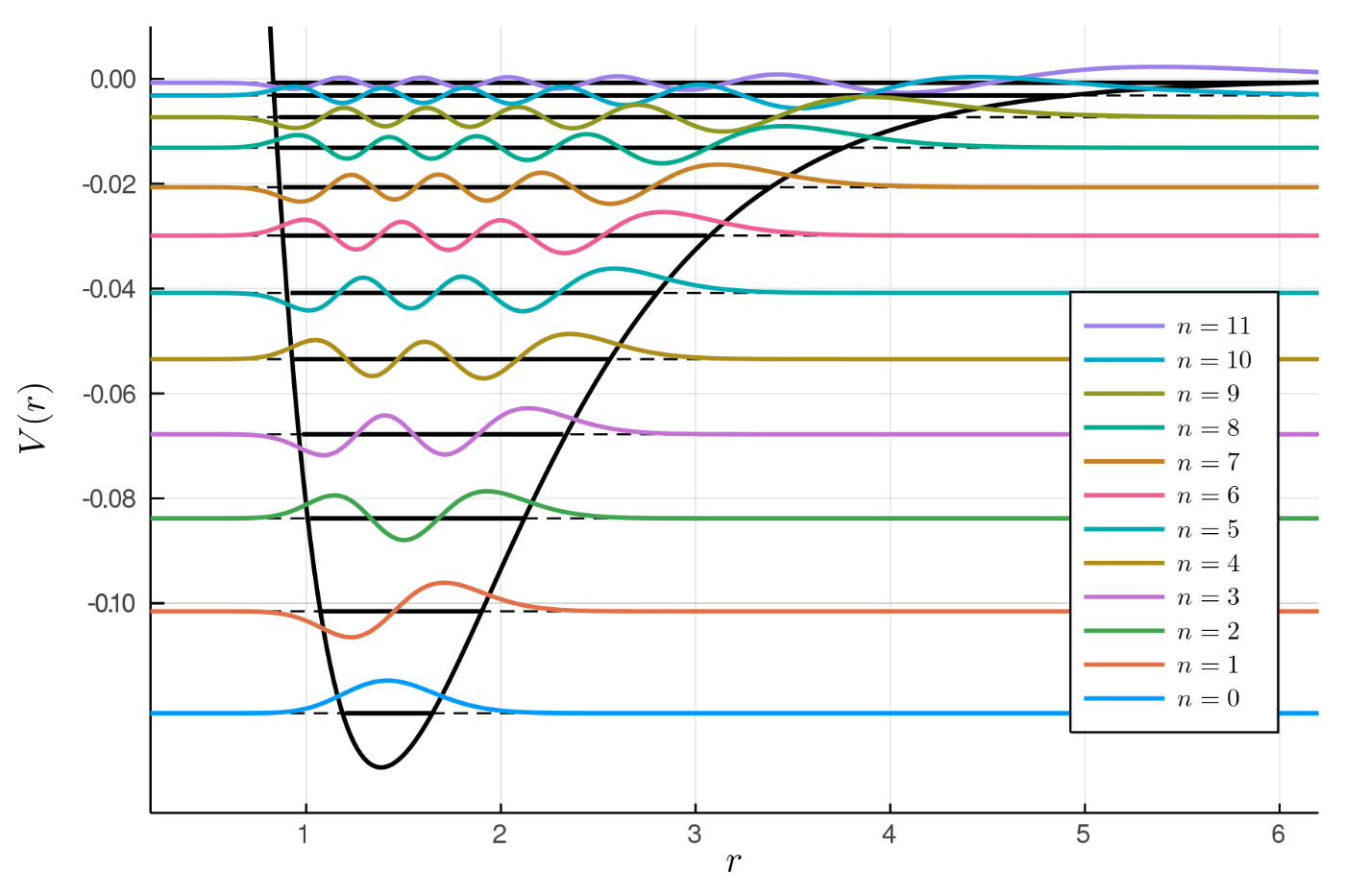
数値積分による検算

固有関数が正しく宣言できているのか見た目だけでは判断できないことが多いので, ライブラリの使い方が正しいか, バグが無いか, 文献に誤りがないか等を確認する意味も含め, 規格化条件\int |\psi_n(x)|^2 \mathrm{d}x=1を満足するか簡単に計算する. 積分は以下のように離散化する. iの範囲は適当に広く取る. 数値積分なので完全に1にはならないが, 概ね1なら問題ない.

\int_0^\infty |\psi(r)|^2 \mathrm{d}r \simeq \sum_{i=0}^\infty |\psi(i \Delta r)|^2 \Delta r 
# 数値積分のルーチン
integral(func, x_min, x_max, dx) = sum(func.(x_min:dx:x_max)*dx)

# 規格化条件の確認

println("n \t∫|ψ(r)|²dr")
for n in 0:11
    println(n, "\t", integral(r->ψ(n,r,re,De,a,µ)^2, -10, 50, 0.001))
end

n 	∫|ψ(r)|²dr
0	1.0000000000000002
1	1.0
2	0.9999999999999998
3	1.0000000000000004
4	1.0
5	0.9999999999999997
6	0.9999999999999999
7	0.9999999999999997
8	0.9999999999999989
9	1.0
10	0.9999999999999999
11	0.9999999999999988

次にエネルギーを数値積分によって評価する. 調和振動子とは違ってビリアル定理が使えないので, 運動項と向き合わなければならない. 2階微分は差分法を用いて

\begin{align} \frac{\mathrm{d}^2\psi(r)}{\mathrm{d}r ^2} &= \frac{ \frac{\psi(r+\Delta r) - \psi(r)}{\Delta r} - \frac{\psi(r) - \psi(r-\Delta r)}{\Delta r} }{\Delta r} \\ &= \frac{\psi(r+\Delta r) - 2\psi(r) + \psi(r-\Delta r)}{\Delta r ^2} \end{align}

と近似できるので, 実関数であること\psi^*(r)=\psi(r)を用いると

\begin{align} \int_0^\infty \psi^*(r) \hat{H} \psi(r) \mathrm{d}r &= \int_0^\infty \psi^*(r) \left[ - \frac{\hbar^2}{2\mu} \frac{\mathrm{d}^2}{\mathrm{d}r ^2} + V(r) \right] \psi(r) \mathrm{d}r \\ &= - \frac{\hbar^2}{2\mu} \int_0^\infty \psi(r) \frac{\mathrm{d}^2 \psi(r)}{\mathrm{d}r ^2} \mathrm{d}r + \int_0^\infty V(r) |\psi(r)|^2 \mathrm{d}r \\ &= - \frac{\hbar^2}{2\mu} \sum_{i=1}^\infty \psi(i\Delta r)\frac{\psi(i\Delta r+\Delta r) - 2\psi(i\Delta r) + \psi(i\Delta r-\Delta r)}{\Delta r ^2} \Delta r + \sum_{i=1}^\infty V(i\Delta r) |\psi(i\Delta r)|^2 \Delta r \end{align}

と離散化できる. ただし, \psi(r)の引数が負とならないように添え字の始まりをiに変更した. \Delta r<<1なのでi=0とi=1ではあまり差は無いはずである. \Delta rの細かさに依るが, 数桁は一致していることが確かめられる.

println("n \tE\t\t\t∫ψHψdr")

dr = 0.005
ψVψ(n,r,re,De,a,µ)    = V(r,re,De,a) * ψ(n,r,re,De,a,µ)^2
ψTψ(n,r,re,De,a,µ,dr) = -1/(2*µ) * ψ(n,r,re,De,a,µ) * (ψ(n,r+dr,re,De,a,µ)-2*ψ(n,r,re,De,a,µ)+ψ(n,r-dr,re,De,a,µ))/dr^2
ψHψ(n,r,re,De,a,µ,dr) = ψTψ(n,r,re,De,a,µ,dr) + ψVψ(n,r,re,De,a,µ)

for n in 0:11
    println(n, "\t", E(n,De,a,µ), "\t", integral(r->ψHψ(n,r,re,De,a,µ,dr), dr, 100, dr))
end

n 	E			∫ψHψdr
0	-0.12098032966578513	-0.12098063308527979
1	-0.10154887790721412	-0.10155018470683336
2	-0.08381744493512158	-0.08382034362426742
3	-0.06778603074950751	-0.06779072698018129
4	-0.05345463535037193	-0.053461018312416515
5	-0.040823258737714835	-0.040830967539695506
6	-0.0298919009115362	-0.02990039094983932
7	-0.020660561871836063	-0.020669171190581332
8	-0.013129241618614396	-0.0131372572629767
9	-0.007297940151871213	-0.0073046645173990635
10	-0.003166657471606507	-0.0031714746521237978
11	-0.0007353935778202786	-0.0007378357145039691

調和近似

このポテンシャルの調和近似に相当する調和振動子ポテンシャルとそのハミルトニアンの固有値および固有関数は

V(r) = V_0 - D_\mathrm{e} + \frac{1}{2} k (r - r_\mathrm{e})^2\\ \psi_n(r) = A_n H_n(\xi) \exp{\left( -\frac{\xi^2}{2} \right)} \\ E_n = V_0 -D_\mathrm{e} + \hbar \omega \left( n + \frac{1}{2} \right)

ただし, \omega:=\sqrt{k/m}, \xi=\sqrt{\frac{m\omega}{\hbar}} (r - r_\mathrm{e}), A_n=\sqrt{\frac{1}{n! 2^n} \sqrt{\frac{m\omega}{\pi\hbar}}}であり, H_nはエルミート多項式である. また,

a = \sqrt{k/2D_\mathrm{e}}

である. エネルギーをモールポテンシャルと比較すると, 第3項（非調和項）のみの違いであることがわかる. また, 調和近似と言ったものの, むしろ先にバネ定数kを決定して上式でaを決定する方が実用的だったりする.

module HO
using SpecialPolynomials

# ポテンシャル
V(r, re, De, k) = - De + 1/2*k*(r-re)^2

# 固有関数
# using SpecialPolynomials
function ψ(r,re,n,k,m)
    ℏ = 1.0
    ω = sqrt(k/m) # mu = 1 / (1/m1 + 1/m2)
    A = sqrt(1/(factorial(n)*2^n)*sqrt(m*ω/(π*ℏ)))
    ξ = sqrt(m*ω/ℏ) * (r-re)
    return A*basis(Hermite, n)(ξ)*exp(-ξ^2/2)
end

# 固有値
function E(n,De,k,m)
    ℏ = 1
    ω = sqrt(k/m)
    return - De + ℏ*ω*(n+1/2)
end

end

描写してモースポテンシャルと比較すると, 極小点ではよく似た形をしていることがわかる.

# 軸ラベル, 描写範囲, 凡例位置
plot(xlabel=L"r", ylabel=L"V(r)", xlims=(0.2,6.2), ylims=(-0.14,0.01), legend=:bottomright)#, size=(450,400))

# ポテンシャル
plot!(0:0.02:7, r->V(r,re,De,a), label="Morse Potential", lc="#578FC7", lw=2)
plot!(0:0.02:7, r->HO.V(r,re,De,k), label="Harmonic Oscillator", lc="#BC1C5F", lw=2)

# 表示
plot!() |> display

次にエネルギーを描写する. 低い準位では, 高い準位に比べればよく一致している. 準位の間隔が一定であるため, 束縛状態の数は少なくなる.

# 軸ラベル, 描写範囲, 凡例位置
plot(xlabel=L"r", ylabel=L"V(r)", xlims=(0.2,6.2), ylims=(-0.14,0.01), legend=:bottomright)#, size=(450,400))

# ポテンシャル
plot!(0:0.02:7, r->V(r,re,De,a), label="Morse Potential", lc="#578FC7", lw=2)
plot!(0:0.02:7, r->HO.V(r,re,De,k), label="Harmonic Oscillator", lc="#BC1C5F", lw=2)

# エネルギー
for n in 11:-1:0
    plot!(0:0.02:7, r-> E(n,De,a,µ)<V(r,re,De,a) ? NaN : E(n,De,a,µ), label="", lc="#578FC7")
end

for n in 5:-1:0
    plot!(0:0.02:7, r-> HO.E(n,De,k,µ)<HO.V(r,re,De,k) ? NaN : HO.E(n,De,k,µ), label="", lc="#BC1C5F")
end

# 表示
plot!() |> display

次に調和振動子の波動関数を描写する.

# 軸ラベル, 描写範囲, 凡例位置
plot(xlabel=L"r", ylabel=L"V(r)", xlims=(0.2,6.2), ylims=(-0.14,0.01), legend=:bottomright)#, size=(450,400))

# ポテンシャル
plot!(-3:0.02:17, r->V(r,re,De,a), label="", lc="#737B85", lw=1, ls=:dash)
plot!(-3:0.02:17, r->HO.V(r,re,De,k), label="", lc="#000000", lw=2)

for n in 11:-1:0
    # エネルギー（実線）
    plot!(0:0.02:7, r-> E(n,De,a,µ)<V(r,re,De,a) ? NaN : E(n,De,a,µ), label="", lc="#737B85", lw=1, ls=:dash)
end

for n in 5:-1:0
    # エネルギー（破線）
    # hline!([HO.E(n,De,k,µ)], label="", lc="#000000", ls=:dash)
    # エネルギー（実線）
    plot!(0:0.02:7, r-> HO.E(n,De,k,µ)<HO.V(r,re,De,k) ? NaN : HO.E(n,De,k,µ), label="", lc="#000000", lw=2)
    # 波動関数
    plot!(0:0.02:7, r->0.004*HO.ψ(r,re,n,k,µ)+HO.E(n,De,k,µ), label=latexstring("n=$n"), lc=n+1, lw=2)
end

# 表示
plot!() |> display

調和振動子の波動関数（破線）とモース振動子の波動関数（実線）を比較すると, 以下のようになる. 低い準位では非調和性が小さく, 調和近似による記述も高い準位に比べれば悪くない. 高い振動準位では, エネルギーの差に加えて, 波動関数の最大値が長距離側へシフトする傾向も顕著に表れる.

# 軸ラベル, 描写範囲, 凡例位置
plot(xlabel=L"r", ylabel=L"V(r)", xlims=(0.2,6.2), ylims=(-0.14,0.01), legend=:bottomright)#, size=(450,400))

# ポテンシャル
plot!(-3:0.02:17, r->V(r,re,De,a), label="", lc="#000000", lw=2)
plot!(-3:0.02:17, r->HO.V(r,re,De,k), label="", lc="#000000", lw=1, ls=:dot)

# 波動関数
for n in 5:-1:0
    plot!(0:0.02:7, r->0.004*HO.ψ(r,re,n,k,µ)+HO.E(n,De,k,µ), label="", lc=n+1, lw=1, ls=:dot)
    plot!(0:0.02:7, r->0.004*ψ(n,r,re,De,a,µ)+E(n,De,a,µ), label=latexstring("n=$n"), lc=n+1, lw=2)
end

# 表示
plot!() |> display

時間に依存するSchrödinger方程式

時間に依存するSchrödinger方程式

i\hbar \frac{\mathrm{d}}{\mathrm{d}t} \varPsi(x,t) = \hat{H} \varPsi(x,t)

の解は一般に

\varPsi(x,t) = \sum_{n=0}^\infty c_n \psi_n(x) \exp\left(-i \frac{E_n}{\hbar} t \right)

である. これが解であることは単に代入すれば示せる（総和と微分演算子が交換可能である条件を確認せよ）. ただし, c_nは初期条件

\varPsi(x,0) = \sum_{n=0}^\infty c_n \psi_n(x)

を定義する係数である.

時間に依存する波動関数
function Ψ(N,t,r,re,De,a,µ) # ← 大文字のΨなので注意
    sum = 0.0 + im*0.0
    for n in 0:N
        sum += c(n) * ψ(n,r,re,De,a,µ) * exp(im*E(n,De,a,µ)*t)
    end
    return sum
end

# 時間発展の描写
function draw(num)
    anim = Animation()
    N = 10
    for i in 0:100
        # 時刻
        t = 10.0*i
        # 描写範囲, タイトルなど
        plt = plot(title="t=$t", xlabel="r", ylabel="V(r)", xlims=(0.2,6.2), ylims=(-0.14,0.01), legend=:bottomright)#, size=(450,400))
        # ポテンシャル
        plot!(0:0.01:17, r->V(r,re,De,a), label="", lc="#000000", lw=2)
        # 実部 Re Ψ(x,t)
        plot!(plt, 0:0.01:7, r->real(Ψ(N,t,r,re,De,a,µ))*0.05 + sum(c.(0:N) .* E.(0:N,De,a,µ)),  label="Re", lc=1)
        # 虚部 Im Ψ(x,t)
        plot!(plt, 0:0.01:7, r->imag(Ψ(N,t,r,re,De,a,µ))*0.05 + sum(c.(0:N) .* E.(0:N,De,a,µ)),  label="Im", lc=2)
        # 確率密度 |Ψ(x,t)|^2
        plot!(plt, 0:0.01:7, r->abs(Ψ(N,t,r,re,De,a,µ))^2*0.05 + sum(c.(0:N) .* E.(0:N,De,a,µ)), label="P(x,t)", lc=3, lw=2)
        # コマの追加
        frame(anim, plt)
    end
    gif(anim, "TDSE_$(num).gif", fps = 20)
end

まず, 初期条件が純粋に基底状態のみ（c_0=1, c_n=0 (n>0)）ならば実部と虚部が交互に入れ替わり, 確率密度としては時間変化しない. このことは有限差分法を勉強すると容易に理解できる.

c(n) = n==0 ? 1 : 0
draw(1)

次に, 基底状態と第1励起状態を等しい割合で混ぜた初期条件(c_0=c_1=0.5, c_n=0 (n>1))を考えると, 振動らしい振る舞いを見せるようになる.

c(n) = n<2 ? 0.5 : 0
draw(2)

最後に, c_0=\frac{1}{2}, c_1=\frac{1}{4}, c_2=\frac{1}{8}, \cdots, c_n=\frac{1}{2^{n+1}}とすると, 調和振動子とは異なる奇妙な動きを見ることができる.

c(n) = 2.0^(-n-1)
draw(3)

動作環境

versioninfo()
出力
    Julia Version 1.6.2
    Commit 1b93d53fc4 (2021-07-14 15:36 UTC)
    Platform Info:
      OS: Windows (x86_64-w64-mingw32)
      CPU: Intel(R) Core(TM) i7-4650U CPU @ 1.70GHz
      WORD_SIZE: 64
      LIBM: libopenlibm
      LLVM: libLLVM-11.0.1 (ORCJIT, haswell)

参考文献

この記事の元になったJupyter Notebookのデータは下記のリンクにある.
https://gist.github.com/ohno/4a59620ed9e32ebd2ba7ef8e4868a0f5

Juliaで可視化シリーズ

https://zenn.dev/ohno/articles/3101433fbe9231
https://zenn.dev/ohno/articles/870b0c2a0af590
https://zenn.dev/ohno/articles/f849d98a7f58a9
https://zenn.dev/ohno/articles/e1103bc0d58ceb

Discussion