Juliaで特殊関数を使う

量子力学にはやたらと特殊関数が登場する. 調和振動子や水素原子などの初歩的な系でさえ可視化に苦労したので, Juliaでの特殊関数の利用方法をまとめておくことにした. コメントに要望などを書き込んで頂ければ追記する.

$H_{0}(x) = 1.0$
$H_{1}(x) = 2.0 x$
$H_{2}(x) = -2.0 + 4.0 x^{2}$
$H_{3}(x) = -12.0 x + 8.0 x^{3}$
$H_{4}(x) = 12.0 - 48.0 x^{2} + 16.0 x^{4}$
$H_{5}(x) = 120.0 x - 160.0 x^{3} + 32.0 x^{5}$
$H_{6}(x) = -120.0 + 720.0 x^{2} - 480.0 x^{4} + 64.0 x^{6}$
$H_{7}(x) = -1680.0 x + 3360.0 x^{3} - 1344.0 x^{5} + 128.0 x^{7}$
$H_{8}(x) = 1680.0 - 13440.0 x^{2} + 13440.0 x^{4} - 3584.0 x^{6} + 256.0 x^{8}$
$H_{9}(x) = 30240.0 x - 80640.0 x^{3} + 48384.0 x^{5} - 9216.0 x^{7} + 512.0 x^{9}$
$\vdots$

パッケージ

Juliaの特殊関数のパッケージはSpecialFunctions.jlである. ガンマ関数, ベッセル関数, 誤差関数, 楕円積分をはじめとし, 多くの特殊関数はこちらのパッケージで利用可能である. しかし, 量子力学に登場するエルミート多項式, ラゲールの陪多項式, ルジャンドルの陪多項式などはサポートされていないので, SpecialPolynomials.jlを利用する. これらの多項式はPolynomials.jlと連携することで, 微分演算や積分演算が可能であり, 文字列として出力することも可能であるから, さらにLatexify.jlと連携することでLaTeX表示も可能である. 今回はLaTeX表示に少し拘り, LaTeXStringsも利用した. 他にもPrintf.jl, Plots.jlを使用した.

# using Pkg
# Pkg.add("Plots")
# Pkg.add("Printf")
# Pkg.add("Latexify")
# Pkg.add("Polynomials")
# Pkg.add("SpecialPolynomials")
# Pkg.add("SpecialFunctions")
using Plots
using Printf
using Latexify
using LaTeXStrings
using Polynomials
using SpecialPolynomials
using SpecialFunctions

LaTeX表示

Latexify.jlに文字列として数式を渡すことで, LaTeX出力してくれる.

latexify("ax^2+bx+c") |> display
latexify("f(x) = 1/2*x") |> display
latexify("f_1(x) = 1/2*x") |> display

$ax^{2} + bx + c$
$f\left( x \right) = \frac{1}{2} \cdot x$
$\mathrm{f\_1}\left( x \right) = \frac{1}{2} \cdot x$

残念なことに$f_1(x)$となってほしいのに$\mathrm{f\_1}(x)$となってしまう. LaTeXStrings.jlを利用すると, そのままLaTeXとして解釈されるので今度は式の方がおかしくなってしまう.

L"f_1(x) = 1/2*x" |> display

$f_1(x) = 1/2*x$

この問題はLaTeXStrings.jlとLatexify.jlをうまく組み合わせると解決できる. env=:rawで1/2*xを\frac{1}{2} xに変換し, latexstring()に渡すことで結合できる. ついでにcdot=falseで掛け算の$\cdot$を非表示にできる.

latexify("1/2*x", env=:raw) |> display
latexstring("f_1(x) = ", latexify("1/2*x", env=:raw)) |> display
latexstring("f_1(x) = ", latexify("1/2*x", env=:raw, cdot=false)) |> display

\frac{1}{2} \cdot x
$f_1(x) = \frac{1}{2} \cdot x$
$f_1(x) = \frac{1}{2} x$

エルミート多項式

エルミート多項式$H_n(x)$は調和振動子のSchrödinger方程式の固有関数に登場する. ロドリゲスの公式では

$$H_n(x) = (-1)^n \mathrm{e}^{x^2} \frac{\mathrm{d}^n}{\mathrm{d}x^n} \mathrm{e}^{-x^2}$$

と表される. SpecialPolynomials.jlでサポートされており, $H_n(x)$はbasis(Hermite, n)(x)のように書けばよい. $n=0\sim5$の実装が正しいか, LaTeXStrings.jlとLatexify.jlを用いて数式を表示して確認した. Wikipediaと見比べて頂きたい.

# using SpecialPolynomials
# using Polynomials
# using Latexify
# using LaTeXStrings
for n in 0:11
    p = basis(Hermite, n)
    q = convert(Polynomial, p)
    latexstring("H_{$n}(x) = ", latexify("$q", env=:raw, cdot=false)) |> display
end

$H_{0}(x) = 1.0$
$H_{1}(x) = 2.0 x$
$H_{2}(x) = -2.0 + 4.0 x^{2}$
$H_{3}(x) = -12.0 x + 8.0 x^{3}$
$H_{4}(x) = 12.0 - 48.0 x^{2} + 16.0 x^{4}$
$H_{5}(x) = 120.0 x - 160.0 x^{3} + 32.0 x^{5}$
$H_{6}(x) = -120.0 + 720.0 x^{2} - 480.0 x^{4} + 64.0 x^{6}$
$H_{7}(x) = -1680.0 x + 3360.0 x^{3} - 1344.0 x^{5} + 128.0 x^{7}$
$H_{8}(x) = 1680.0 - 13440.0 x^{2} + 13440.0 x^{4} - 3584.0 x^{6} + 256.0 x^{8}$
$H_{9}(x) = 30240.0 x - 80640.0 x^{3} + 48384.0 x^{5} - 9216.0 x^{7} + 512.0 x^{9}$
$H_{10}(x) = -30240.0 + 302400.0 x^{2} - 403200.0 x^{4} + 161280.0 x^{6} - 23040.0 x^{8} + 1024.0 x^{10}$
$H_{11}(x) = -665280.0 x + 2.2176e6 x^{3} - 1.77408e6 x^{5} + 506880.0 x^{7} - 56320.0 x^{9} + 2048.0 x^{11}$

例えば$H_2(x) = 4x^2 - 2$なので, $H_2(5) = 98$となるはずである.

# using SpecialPolynomials
p = basis(Hermite, 2)
p(5)

出力

    98.0

応用例

https://zenn.dev/ohno/articles/870b0c2a0af590

ラゲール多項式

注意せよ. 文献によって$1/n!$が有ったり無かったりする. SpecialPolynomials.jlでサポートされているのはロドリゲスの公式

$$L_n(x) = \frac{1}{n!} \mathrm{e}^x \frac{\mathrm{d}^n}{\mathrm{d}x ^n} \left( \mathrm{e}^{-x} x^n \right)$$

に対応する式であり, $L_n(x)$はbasis(Laguerre{0}, n)(x)のように書けばよい. Wikipedia(英語版)と見比べて頂きたい.

# using SpecialPolynomials
# using Polynomials
# using Latexify
# using LaTeXStrings
for n in 0:7
    p = basis(Laguerre{0}, n)
    q = convert(Polynomial, p)
    latexstring("L_{$n}(x) = ", latexify("$q", env=:raw, cdot=false)) |> display
end

$L_{0}(x) = 1.0$
$L_{1}(x) = 1.0 - 1.0 x$
$L_{2}(x) = 1.0 - 2.0 x + 0.5 x^{2}$
$L_{3}(x) = 1.0 - 3.0 x + 1.5 x^{2} - 0.166667 x^{3}$
$L_{4}(x) = 1.0 - 4.0 x + 3.0 x^{2} - 0.666667 x^{3} + 0.0416667 x^{4}$
$L_{5}(x) = 1.0 - 5.0 x + 5.0 x^{2} - 1.66667 x^{3} + 0.208333 x^{4} - 0.00833333 x^{5}$
$L_{6}(x) = 1.0 - 6.0 x + 7.5 x^{2} - 3.33333 x^{3} + 0.625 x^{4} - 0.05 x^{5} + 0.00138889 x^{6}$
$L_{7}(x) = 1.0 - 7.0 x + 10.5 x^{2} - 5.83333 x^{3} + 1.45833 x^{4} - 0.175 x^{5} + 0.00972222 x^{6} - 0.000198413 x^{7}$

$1/n!$について補足する. ラゲール多項式$L_n(x)$はそもそも微分方程式

$$xy'' + (1-x)y' + ny = 0$$

を満たす解$y$であるから, 定数$1/n!$倍だけ異なっても解であることには違いない. もし

$$\tilde{L}_n(x) = n!\cdot L_n(x) = \mathrm{e}^x \frac{\mathrm{d}^n}{\mathrm{d}x ^n} \left( \mathrm{e}^{-x} x^n \right)$$

を利用したいのであれば$L_n(x)$に$n!$を掛ければよいので, factorial(n)*basis(Laguerre{0}, n)(x)とすればよい. Wikipedia(日本語版)の$k=0$の場合と見比べて頂きたい.

# using SpecialPolynomials
# using Polynomials
# using Latexify
# using LaTeXStrings
for n in 0:7
    p = factorial(n)*basis(Laguerre{0}, n)
    q = convert(Polynomial, p)
    latexstring("\\tilde{L}_{$n}(x) = ", latexify("$q", env=:raw, cdot=false)) |> display
end

$\tilde{L}_{0}(x) = 1.0$
$\tilde{L}_{1}(x) = 1.0 - 1.0 x$
$\tilde{L}_{2}(x) = 2.0 - 4.0 x + 1.0 x^{2}$
$\tilde{L}_{3}(x) = 6.0 - 18.0 x + 9.0 x^{2} - 1.0 x^{3}$
$\tilde{L}_{4}(x) = 24.0 - 96.0 x + 72.0 x^{2} - 16.0 x^{3} + 1.0 x^{4}$
$\tilde{L}_{5}(x) = 120.0 - 600.0 x + 600.0 x^{2} - 200.0 x^{3} + 25.0 x^{4} - 1.0 x^{5}$
$\tilde{L}_{6}(x) = 720.0 - 4320.0 x + 5400.0 x^{2} - 2400.0 x^{3} + 450.0 x^{4} - 36.0 x^{5} + 1.0 x^{6}$
$\tilde{L}_{7}(x) = 5040.0 - 35280.0 x + 52920.0 x^{2} - 29400.0 x^{3} + 7350.0 x^{4} - 882.0 x^{5} + 49.0 x^{6} - 1.0 x^{7}$

ラゲールの陪多項式

ラゲールの陪多項式$L_n^k(x)$は水素原子のSchrödinger方程式の固有関数の動径部分に登場する. これは定義ではないが, ラゲール多項式$L_n(x)$との関係

$$L_n^{k}(x) = \frac{\mathrm{d}^k}{\mathrm{d}x^k} L_n(x)$$

が知られている. SpecialPolynomials.jlでは一般化ラゲール多項式$L_n^{(\alpha)}(x)$が実装されているので, $L_n^{k}(x) = L_{n-k}^{(k)}(x)$という関係を利用すればよい. $L_n^{k}(x)$はbasis(Laguerre{k}, n-k)(x)である.

# using SpecialPolynomials
# using Polynomials
# using Latexify
# using LaTeXStrings
for n in 0:4
    for k in 0:n
        p = basis(Laguerre{k}, n-k)
        q = convert(Polynomial, p)
        latexstring("L_$n^$k(x) = ", latexify("$q", env=:raw, cdot=false)) |> display
    end
end

$L_0^0(x) = 1.0$
$L_1^0(x) = 1.0 - 1.0 x$
$L_1^1(x) = 1.0$
$L_2^0(x) = 1.0 - 2.0 x + 0.5 x^{2}$
$L_2^1(x) = 2.0 - 1.0 x$
$L_2^2(x) = 1.0$
$L_3^0(x) = 1.0 - 3.0 x + 1.5 x^{2} - 0.166667 x^{3}$
$L_3^1(x) = 3.0 - 3.0 x + 0.5 x^{2}$
$L_3^2(x) = 3.0 - 1.0 x$
$L_3^3(x) = 1.0$
$L_4^0(x) = 1.0 - 4.0 x + 3.0 x^{2} - 0.666667 x^{3} + 0.0416667 x^{4}$
$L_4^1(x) = 4.0 - 6.0 x + 2.0 x^{2} - 0.166667 x^{3}$
$L_4^2(x) = 6.0 - 4.0 x + 0.5 x^{2}$
$L_4^3(x) = 4.0 - 1.0 x$
$L_4^4(x) = 1.0$

Polynomials.jlのderivative(q,k)を用いてラゲール多項式$L_n(x)$の$k$階の導関数を計算しても, 同様の結果が得られる.

# using SpecialPolynomials
# using Polynomials
# using Latexify
# using LaTeXStrings
for n in 0:4
    for k in 0:n
        p = basis(Laguerre{0}, n)
        q = convert(Polynomial, p)
        r = derivative(q,k)
        latexstring("L_$n^$k(x) = ", latexify("$r", env=:raw, cdot=false)) |> display
    end
end

$L_0^0(x) = 1.0$
$L_1^0(x) = 1.0 - 1.0 x$
$L_1^1(x) = -1.0$
$L_2^0(x) = 1.0 - 2.0 x + 0.5 x^{2}$
$L_2^1(x) = -2.0 + 1.0 x$
$L_2^2(x) = 1.0$
$L_3^0(x) = 1.0 - 3.0 x + 1.5 x^{2} - 0.166667 x^{3}$
$L_3^1(x) = -3.0 + 3.0 x - 0.5 x^{2}$
$L_3^2(x) = 3.0 - 1.0 x$
$L_3^3(x) = -1.0$
$L_4^0(x) = 1.0 - 4.0 x + 3.0 x^{2} - 0.666667 x^{3} + 0.0416667 x^{4}$
$L_4^1(x) = -4.0 + 6.0 x - 2.0 x^{2} + 0.166667 x^{3}$
$L_4^2(x) = 6.0 - 4.0 x + 0.5 x^{2}$
$L_4^3(x) = -4.0 + 1.0 x$
$L_4^4(x) = 1.0$

応用例

https://zenn.dev/ohno/articles/e1103bc0d58ceb#動径関数

一般化ラゲール多項式

一般化ラゲール多項式$L_n^{(\alpha)}(x)$は水素原子やモースポテンシャルを考えるときに登場する.
Generalized Laguerre polynomialsの和訳. 少なくともGoogle翻訳ではラゲールの陪多項式と訳されるが, 日本で使われているラゲールの陪多項式とは定義が違うようなので, 注意されたい. 調査したところ, かなり紛らわしいので, 一般化ラゲール多項式$L_n^{(\alpha)}(x)$とラゲールの陪多項式$L_n^k(x)$は別物と考えた方がすっきりする.「どうせ$k\in\mathbb{N}$と$k\in\mathbb{R}$の違いだろう」などと決めつけてかかると痛い目を見る.

前提

まず, 一般化ラゲール多項式$L_n^{(\alpha)}(x)$とラゲールの陪多項式$L_n^k(x)$はそもそも満たすべき方程式が異なる.

多項式	満たすべき方程式	出典
ラゲール多項式$L_n(x)$	$$xy'' + (1-x)y' + ny = 0$$
ラゲールの陪多項式$L_n^k(x)$	$$xy'' + (k+1-x)y' + (n-k)y = 0$$	日本語のWikipedia
Generalized Laguerre polynomials 一般化ラゲール多項式$L_n^{(\alpha)}(x)$	$$xy'' + (\alpha+1-x)y' + ny = 0$$	英語のWikipedia

共通点

ラゲールの陪多項式$L_n^k(x)$も一般化ラゲール多項式$L_n^{(\alpha)}(x)$も$k=\alpha=0$のときにラゲール多項式$L_n(x)$に一致するように一般化されていることが明らかである.

$$L_n(x) = L_n^{0}(x) = L_n^{(0)}(x)$$

ラゲール多項式$L_n(x)$の定義が$L_n(x) = \frac{1}{n!} \mathrm{e}^x \frac{\mathrm{d}^n}{\mathrm{d}x ^n} \left( \mathrm{e}^{-x} x^n \right)$ではなく$L_n(x) = \mathrm{e}^x \frac{\mathrm{d}^n}{\mathrm{d}x ^n} \left( \mathrm{e}^{-x} x^n \right)$のときは

$$L_n(x) = L_n^{0}(x) = n! L_n^{(0)}(x)$$

であることに注意.

相違点

一般化ラゲール多項式$L_n^{(\alpha)}(x)$はラゲールの陪多項式$L_n^k(x)$とは異なり, $\alpha\in\mathbb{N}$に限定したとしてもラゲール多項式$L_n(x)$の導関数ではない.

$$\begin{align} L_n^{k}(x) &= \frac{\mathrm{d}^k}{\mathrm{d}x^k} L_n(x)\\ L_n^{(\alpha)}(x) &\neq \frac{\mathrm{d}^\alpha}{\mathrm{d}x^\alpha} L_n(x) \end{align}$$

これは, そもそも満たすべき方程式が違うためである. 逆に言うと, ラゲールの陪多項式$L_n^k(x)$もガンマ関数を用いて$k\in\mathbb{R}$で成り立つようにしてやれば(実際, ライブラリでは成り立つ), 満たすべき方程式以外に違いは無いともいえる. そうすると, 満たすべき方程式がどちらなのか確認さえすれば問題ない, ように考えがちだが, ラゲール多項式$L_n(x)$の$1/n!$の有無も文献によるので慎重になった方がよい.

対応関係

見ての通り, ラゲールの陪多項式$L_n^k(x)$と一般化ラゲール多項式$L_n^{(\alpha)}(x)$は異なる性質を持つが, これらの間には次の関係が明らかに成り立つ.

$$L_n^{k}(x) = L_{n-k}^{(k)}(x)$$

ラゲール多項式$L_n(x)$の定義が$L_n(x) = \frac{1}{n!} \mathrm{e}^x \frac{\mathrm{d}^n}{\mathrm{d}x ^n} \left( \mathrm{e}^{-x} x^n \right)$ではなく$L_n(x) = \mathrm{e}^x \frac{\mathrm{d}^n}{\mathrm{d}x ^n} \left( \mathrm{e}^{-x} x^n \right)$のときは

$$L_n^{k}(x) = n! L_{n-k}^{(k)}(x)$$

であることに注意.

このことから, 水素原子の動径関数は多くが$L_{n+l}^{2l+1}(x)$であるが, たまに$L_{n-l-1}^{(2n+l)}(x)$のパターンがある. 前者は『マッカーリ・サイモン物理化学 上』p.224, 『アトキンス 物理化学（上）第10版』p.381, 原田義也『量子化学 上巻』(第2版, 2019, 裳華房) p.123, 高柳和夫『原子分子物理学』(2000, 朝倉書店) p.16, Wikipedia(日本語)などであり, 後者がこちらのサイトやWikipedia(英語)である.
この違いを抜きにしても規格化定数が間違っていたりするので, 数値積分などで簡単にでも確認した方がよい.

使用法

SpecialPolynomials.jlでサポートされており, $L_n^{(\alpha)}(x)$はそのままbasis(Laguerre{α}, n)(x)である. もちろん$\alpha\in\mathbb{R}$で使える.

# using SpecialPolynomials
# using Polynomials
# using Latexify
# using LaTeXStrings
for n in 0:4
    for k in 0:n
        p = basis(Laguerre{k}, n)
        q = convert(Polynomial, p)
        latexstring("L_$n^{($k)}(x) = ", latexify("$q", env=:raw, cdot=false)) |> display
    end
end

$L_0^{(0)}(x) = 1.0$
$L_1^{(0)}(x) = 1.0 - 1.0 x$
$L_1^{(1)}(x) = 2.0 - 1.0 x$
$L_2^{(0)}(x) = 1.0 - 2.0 x + 0.5 x^{2}$
$L_2^{(1)}(x) = 3.0 - 3.0 x + 0.5 x^{2}$
$L_2^{(2)}(x) = 6.0 - 4.0 x + 0.5 x^{2}$
$L_3^{(0)}(x) = 1.0 - 3.0 x + 1.5 x^{2} - 0.166667 x^{3}$
$L_3^{(1)}(x) = 4.0 - 6.0 x + 2.0 x^{2} - 0.166667 x^{3}$
$L_3^{(2)}(x) = 10.0 - 10.0 x + 2.5 x^{2} - 0.166667 x^{3}$
$L_3^{(3)}(x) = 20.0 - 15.0 x + 3.0 x^{2} - 0.166667 x^{3}$
$L_4^{(0)}(x) = 1.0 - 4.0 x + 3.0 x^{2} - 0.666667 x^{3} + 0.0416667 x^{4}$
$L_4^{(1)}(x) = 5.0 - 10.0 x + 5.0 x^{2} - 0.833333 x^{3} + 0.0416667 x^{4}$
$L_4^{(2)}(x) = 15.0 - 20.0 x + 7.5 x^{2} - 1.0 x^{3} + 0.0416667 x^{4}$
$L_4^{(3)}(x) = 35.0 - 35.0 x + 10.5 x^{2} - 1.16667 x^{3} + 0.0416667 x^{4}$
$L_4^{(4)}(x) = 70.0 - 56.0 x + 14.0 x^{2} - 1.33333 x^{3} + 0.0416667 x^{4}$

応用例

https://zenn.dev/ohno/articles/f849d98a7f58a9#可視化

ルジャンドル多項式

ルジャンドル多項式$P_n$はロドリゲスの公式

$$P_n(x) = \frac{1}{2^n n!} \frac{\mathrm{d}^n}{\mathrm{d}x ^n} \left[ \left( x^2-1 \right)^n \right]$$

で与えられる. $P_n(x)$はbasis(Legendre, n)(x)のように書けばよい.
こちらと見比べて頂きたい.

# using SpecialPolynomials
# using Polynomials
# using Latexify
# using LaTeXStrings
for n in 0:11
    p = basis(Legendre, n)
    q = convert(Polynomial, p)
    latexstring("P_{$n}(x) = ", latexify("$q", env=:raw, cdot=false)) |> display
end

$P_{0}(x) = 1.0$
$P_{1}(x) = 1.0 x$
$P_{2}(x) = -0.5 + 1.5 x^{2}$
$P_{3}(x) = -1.5 x + 2.5 x^{3}$
$P_{4}(x) = 0.375 - 3.75 x^{2} + 4.375 x^{4}$
$P_{5}(x) = 1.875 x - 8.75 x^{3} + 7.875 x^{5}$
$P_{6}(x) = -0.3125 + 6.5625 x^{2} - 19.6875 x^{4} + 14.4375 x^{6}$
$P_{7}(x) = -2.1875 x + 19.6875 x^{3} - 43.3125 x^{5} + 26.8125 x^{7}$
$P_{8}(x) = 0.273438 - 9.84375 x^{2} + 54.1406 x^{4} - 93.8438 x^{6} + 50.2734 x^{8}$
$P_{9}(x) = 2.46094 x - 36.0938 x^{3} + 140.766 x^{5} - 201.094 x^{7} + 94.9609 x^{9}$
$P_{10}(x) = -0.246094 + 13.5352 x^{2} - 117.305 x^{4} + 351.914 x^{6} - 427.324 x^{8} + 180.426 x^{10}$
$P_{11}(x) = -2.70703 x + 58.6523 x^{3} - 351.914 x^{5} + 854.648 x^{7} - 902.129 x^{9} + 344.449 x^{11}$

ルジャンドルの陪多項式

ルジャンドルの陪多項式$P_k^m(t)$は球面調和関数すなわち水素原子の軌道の角度部分に登場する. ルジャンドル多項式$P_n$との関係が次式で与えられている.

$$P_k^m(t) = \left( 1-t^2 \right)^{m/2} \frac{\mathrm{d}^m P_k(t)}{\mathrm{d}t^m}$$

なお, Wikipediaの英語版だと符号がつけ加えられているが, 結局は線形微分方程式の解なので定数倍の違いは著者の好みに委ねられてしまう. 定義が違えば球面調和関数の規格化定数も変わるので注意されたい.

$$P_k^m(t) = (-1)^m \left( 1-t^2 \right)^{m/2} \frac{\mathrm{d}^m P_k(t)}{\mathrm{d}t^m}$$

ここでは英語版の定義を採用する. こちらと比較して頂きたい.

# using SpecialPolynomials
# using Polynomials
# using Latexify
# using LaTeXStrings
for k in 0:4
    for m in 0:k
        p = basis(Legendre, k)
        q = convert(Polynomial, p)
        r = derivative(q, abs(m))
        if m % 2 == 0
            s = (-1)^m*(Polynomial([1,-2]))^(Int(m/2))*r
            latexstring("P_{$k}^{$m}(x) = ", latexify("$s", env=:raw, cdot=false)) |> display
        else
            s = (-1)^m*(Polynomial([1,-2]))^(Int((m-1)/2))*r
            latexstring("P_{$k}^{$m}(x) = \\left(", latexify("$s", env=:raw, cdot=false), "\\right)\\sqrt{1-x^2}") |> display
        end
    end
end

$P_{0}^{0}(x) = 1.0$
$P_{1}^{0}(x) = 1.0 x$
$P_{1}^{1}(x) = \left(-1.0\right)\sqrt{1-x^2}$
$P_{2}^{0}(x) = -0.5 + 1.5 x^{2}$
$P_{2}^{1}(x) = \left(-3.0 x\right)\sqrt{1-x^2}$
$P_{2}^{2}(x) = 3.0 - 6.0 x$
$P_{3}^{0}(x) = -1.5 x + 2.5 x^{3}$
$P_{3}^{1}(x) = \left(1.5 - 7.5 x^{2}\right)\sqrt{1-x^2}$
$P_{3}^{2}(x) = 15.0 x - 30.0 x^{2}$
$P_{3}^{3}(x) = \left(-15.0 + 30.0 x\right)\sqrt{1-x^2}$
$P_{4}^{0}(x) = 0.375 - 3.75 x^{2} + 4.375 x^{4}$
$P_{4}^{1}(x) = \left(7.5 x - 17.5 x^{3}\right)\sqrt{1-x^2}$
$P_{4}^{2}(x) = -7.5 + 15.0 x + 52.5 x^{2} - 105.0 x^{3}$
$P_{4}^{3}(x) = \left(-105.0 x + 210.0 x^{2}\right)\sqrt{1-x^2}$
$P_{4}^{4}(x) = 105.0 - 420.0 x + 420.0 x^{2}$

関数として利用する場合は次のようにする.

# using SpecialPolynomials
# using Polynomials
function P(k,m,x)
    if m<0
        return (-1)^m * factorial(l-m) / factorial(l+m) * P(k,m,x)
    end
    p = basis(Legendre, k)
    q = convert(Polynomial, p)
    r = derivative(q, abs(m))
    return (-1)^m * (1-x^2)^(m/2) * r(x)
end

# Plots
for m in 0:2
    plot(title=latexstring("m=$m"), xlabel=L"x", ylabel=latexstring("P_k^m(x)"), xlims=(-1,1), ylims=(-[1.2,3,15][m+1],[1.2,3,23][m+1]), legend=:bottomright)
    for k in 0:[4,5,6][m+1]
        plot!(x->P(k,m,x), label=latexstring("k=$k"), lw=2)
    end
    plot!() |> display
end

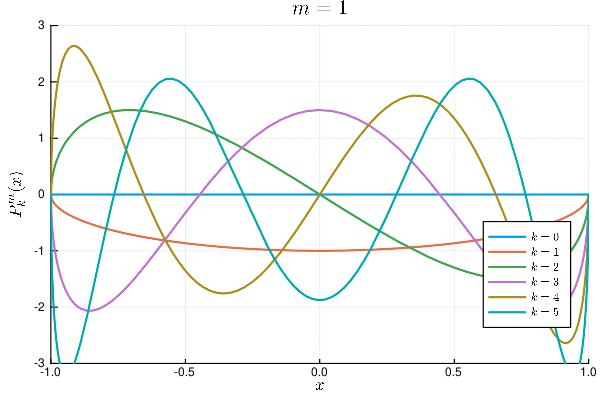
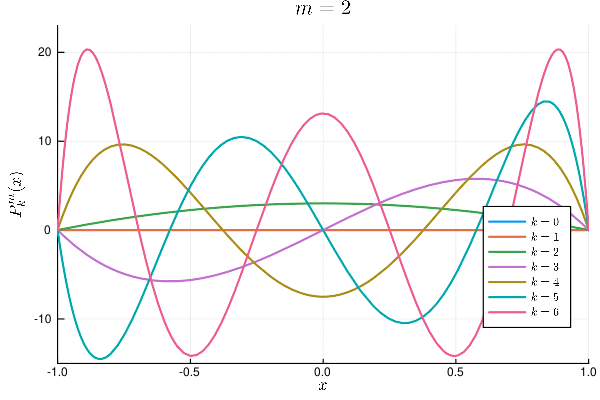
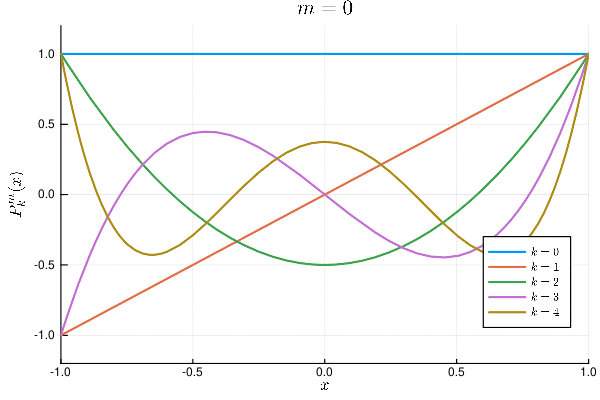
応用例

https://zenn.dev/ohno/articles/e1103bc0d58ceb#球面調和関数

ガンマ関数

ガンマ関数$\Gamma(x)$はモールポテンシャルの波動関数にも登場する. 階乗の一般化であり, $\Gamma(n) = (n-1)!$という関係が成立する. まずこれを確認する. Juliaでは階乗はfactorial(x)で利用できる. ガンマ関数はSpecialFunctions.jlでサポートされており, gamma(x)である.

# using SpecialFunctions
println("n\tn!\tΓ(n)")
for i in 1:9
    x = factorial(i-1)
    y = gamma(i)
    println("$i\t$x\t$y")
end

出力

    n	(n-1)!	Γ(n)
    1	1	1.0
    2	1	1.0
    3	2	2.0
    4	6	6.0
    5	24	24.0
    6	120	120.0
    7	720	720.0
    8	5040	5040.0
    9	40320	40320.0

非整数についても$\Gamma(1/2) = \sqrt{\pi}$などが成り立つことが確認できる.

# using SpecialFunctions
gamma(1/2)^2

出力

    3.1415926535897936

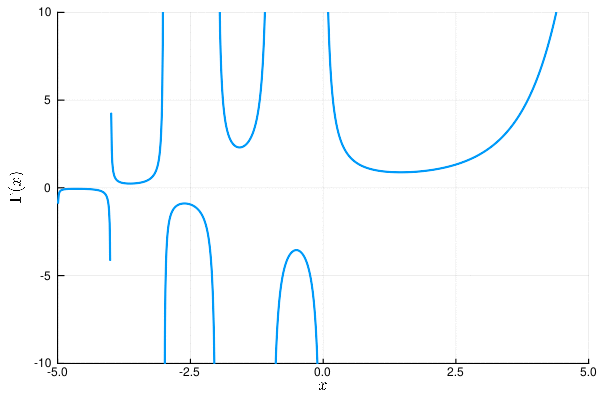
描写すると次のようなグラフになる. こちらと見比べて頂きたい.

plot(zlims=(0,6), xlabel=L"y", ylabel=L"x", zlabel=L"|\Gamma(x+iy)|", camera=(45,30))
wireframe!(-5:0.2:5, -5:0.05:5, (y,x)->abs(gamma(x+im*y)))

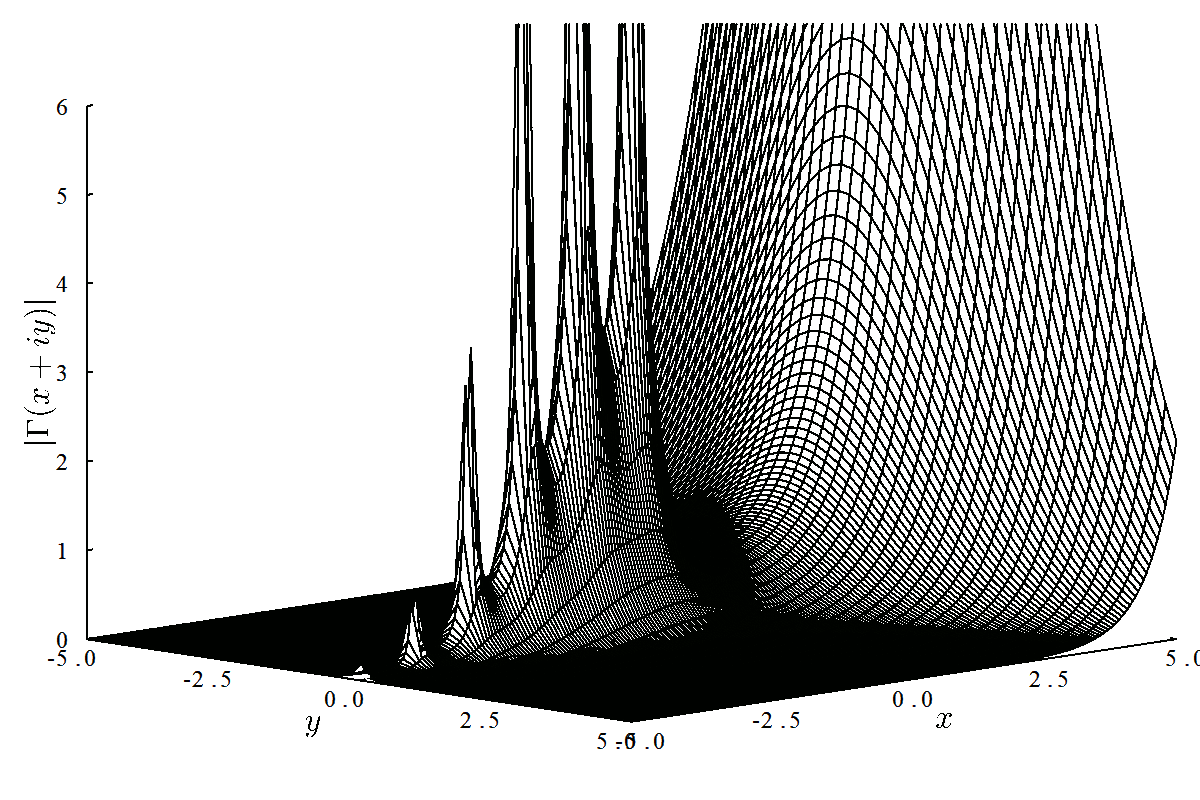
Γ(z) = try; gamma(z); catch; NaN; end
plot(xlims=(-5,5), ylims=(-10,10), xlabel=L"x", ylabel=L"\Gamma(x)")
plot!(-5:0.01:5, x->Γ(x), label="", lw=2)

誤差関数

誤差関数はHartree-Fock法の核-電子間引力の積分などに登場する. SpecialFunctions.jlでサポートされており, 誤差関数はerf(x), 相補誤算関数はerfc(x)である. たまにお世話になるので一応, 簡単な数値積分を用いて検証しておく.

$$\mathrm{erf}(x) = \frac{2}{\sqrt{\pi}} \int_0^x \exp(-t^2) \mathrm{d}t\\ \mathrm{erfc}(x) = 1 - \mathrm{erf}(x)$$

# 数値積分のルーチン
function integral(func, x_min, x_max, dx)
    sum = 0.0
    for x in x_min:dx:x_max
        sum += func(x)*dx
    end
    return sum
end

# using SpecialFunctions
# using Printf
@printf("%-9s\t%-9s\t%-9s\t%-9s\n", " x", " erf(x)", " 1-erfc(x)", " integral")
for x in 0:0.5:3
    @printf("%9f\t%9f\t%9f\t%9f\n", x, erf(x), 1-erfc(x), 2/sqrt(pi)*integral(t->exp(-t^2), 0, x, 0.0000001))
end

出力

     x       	 erf(x)  	 1-erfc(x)	 integral
     0.000000	 0.000000	 0.000000	 0.000000
     0.500000	 0.520500	 0.520500	 0.520500
     1.000000	 0.842701	 0.842701	 0.842701
     1.500000	 0.966105	 0.966105	 0.966105
     2.000000	 0.995322	 0.995322	 0.995322
     2.500000	 0.999593	 0.999593	 0.999593
     3.000000	 0.999978	 0.999978	 0.999978

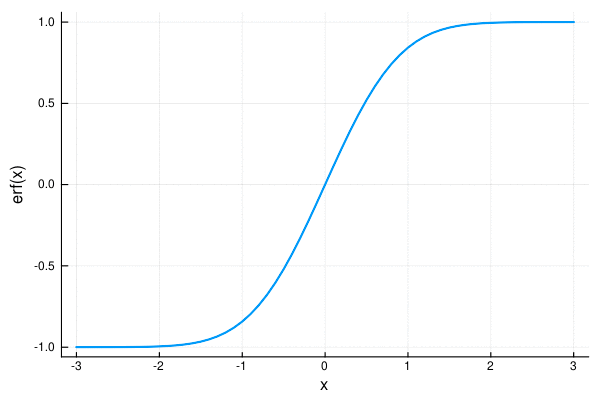
plot(-3:0.1:3, erf, xlabel="x", ylabel="erf(x)", label="", lw=2) |> display
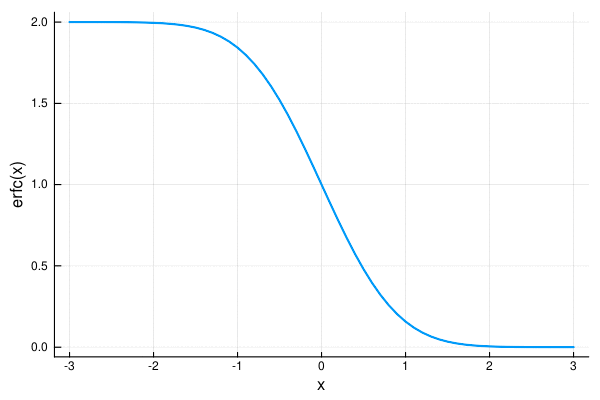
plot(-3:0.1:3, erfc, xlabel="x", ylabel="erfc(x)", label="", lw=2) |> display

動作環境

versioninfo()

出力

    Julia Version 1.6.2
    Commit 1b93d53fc4 (2021-07-14 15:36 UTC)
    Platform Info:
      OS: Windows (x86_64-w64-mingw32)
      CPU: Intel(R) Core(TM) i7-4650U CPU @ 1.70GHz
      WORD_SIZE: 64
      LIBM: libopenlibm
      LLVM: libLLVM-11.0.1 (ORCJIT, haswell)

参考文献

• SpecialFunctions.jl
• SpecialPolynomials.jl
• Polynomials.jl, 微分演算, 積分演算
• Latexify.jl
• LaTeXStrings
• ガンマ関数
• ラゲールの陪多項式
• 水素原子のSchrödinger方程式の固有関数の動径部分
• Generalized Laguerre polynomials
• ルジャンドル多項式
• ルジャンドルの陪多項式
• 球面調和関数
• Plots.jl入門

この記事の元になったJupyter Notebookのデータは下記のリンクにある.
https://gist.github.com/ohno/1ed4da972acbc988bc318fc53647afac