【Python】水素原子の可視化：球面調和関数

球面調和関数

この記事は消化不良の箇所を一部含みますが、他の方の役に立つ部分もあると思うので公開します。分からなかったところは分からなかったと記載しています。私の理解が進んだら記事を改定するかもしれません。間違いなどを見つけた方はコメント欄やTwitterなどでご連絡頂けますと幸いです。

0. 概要

この記事では、シュレディンガー方程式に従う水素原子の解を描画する、という立場に立ち、球面調和関数(Spherical harmonics function)に関する情報を整理・解説する。水素原子の解のうち、動径方向に関する部分は以前の記事を参考にされたい。なお、水素原子の解の計算にはscipy(python)ライブラリの球面調和関数計算モジュール(scipy.special.sph_harm)を使用する。球面調和関数の描画はmatplotlib(python)を使用した。

pythonで球面調和関数を描画する上での注意点は下記の３点である。この記事ではこの３点について解説する。

1. Scipyライブラリの仕様
2. 球面調和関数の“何の情報”を描画するのが適切か？
3. デフォルトのカラープロット機能では意図した描画ができない

1.を挙げた理由としては、他の方が書かれた記事でも言及されているが、特殊関数は資料によって定義の揺れが大きく(例えば参考[2,3])、公式helpを注意深く読まないと意図した計算ができないためである。
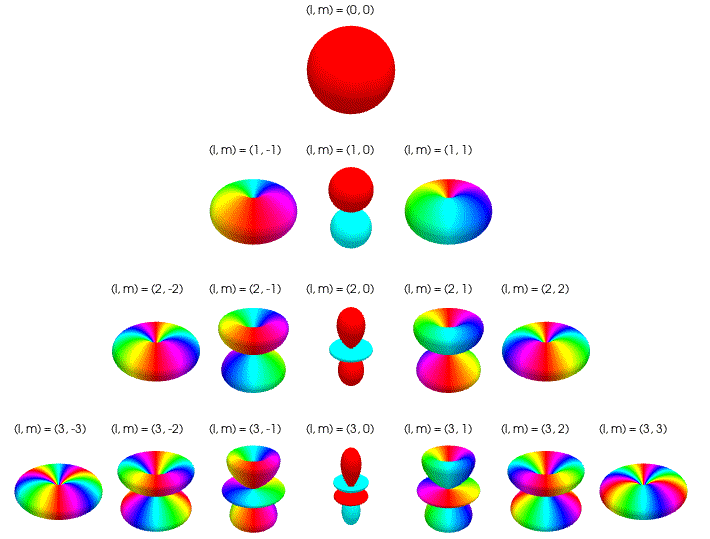
2.を挙げた理由としては、球面調和関数の描画方法はざっと調べた限りでも表1に示す通り7通りあり(参考[4])、初めて描画する際はどれを採用すべきか戸惑う可能性があるためである。

表1. 球面調和関数の描画方法(wikipediaより引用:参考[4])
1, 2.が解決したとして、実際にグラフにして描画できるかは別問題である。実際、水素原子の球面調和関数を描画する際はmatplotlibのデフォルトの機能(plot_surfaceのcmap, color等)ではz軸の値に依存した色付けになってしまい、意図した描画ができない(図1の右側の図)。水素原子の球面調和関数をプロットする際は、図1の左側の図のように球面調和関数の符号(位相)に依存した色付けをするのが適切であるが、これにはカラーパレットのカスタマイズが必要である。ただ、カラーパレットのカスタマイズ方法はscipy公式ヘルプでもしっかりとした説明がなされておらず(参考[5])、ネット上に散らばっている情報自体も日本語・英語含めて少ない。これが3.を挙げた理由である。

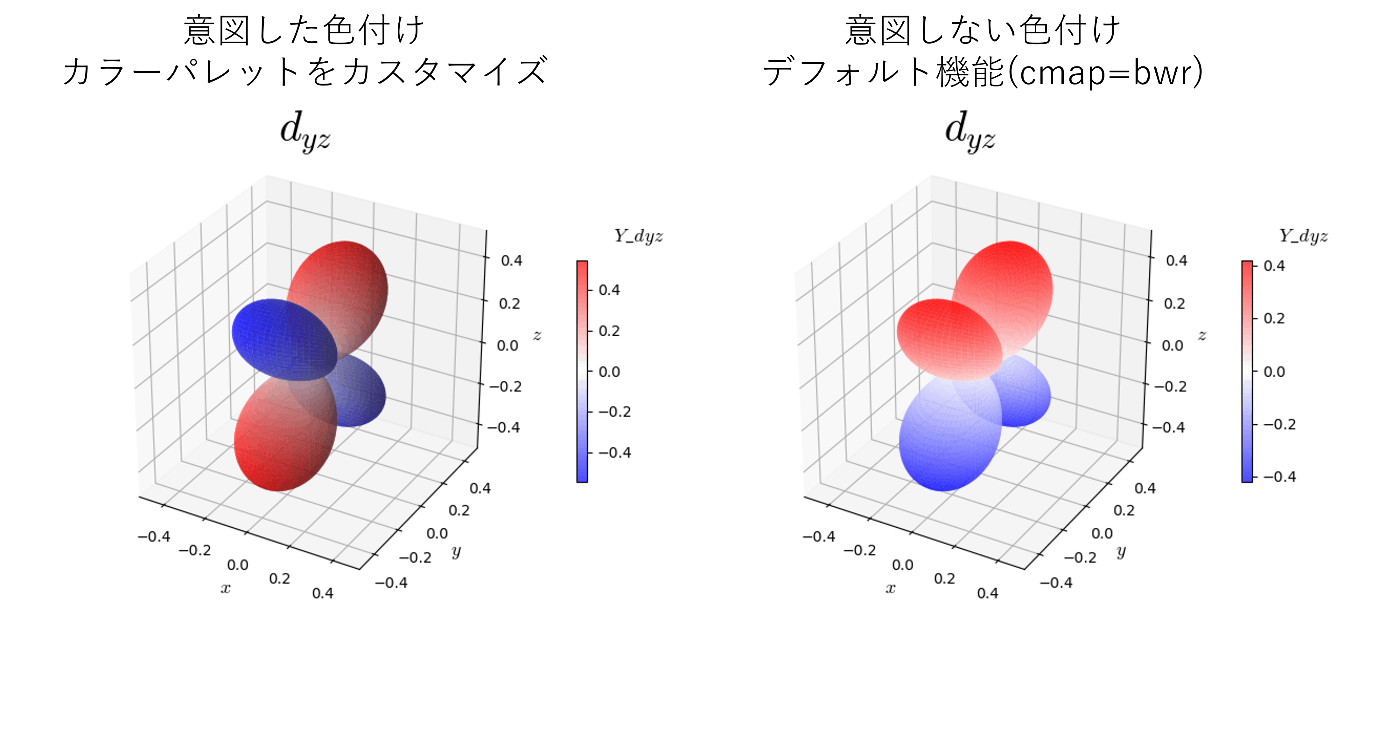
図1. 球面調和関数の意図した色付けと意図しない色付け

1. Scipyライブラリの仕様：球面調和関数

1-1. 球面調和関数の定義

Scipyライブラリを使用する以前に、球面調和関数がどのように定義されているかを整理する。結論から言うと、私が調べた範囲内だと(参考[1,6-12])、ランダウの教科書(参考[12])以外、球面調和関数$Y_l^m(\theta, \phi)$とその定義に使用されるルジャンドル多項式$P_l(x)$は同じものになる。見かけ上、式の形は違って見えるが、具体的に式を書き下すと係数含めて全て同じものになる。ランダウの教科書では球面調和関数の定義が他の資料(参考[1,6-11])と係数$i^l$だけ異なる。係数$i^l$の分だけ異なる定義をしている理由について、ランダウの教科書では理由が述べられている(参考[12,13])。

一方、球面調和関数の定義に使用されるルジャンドル陪多項式(Associated Legendre polynomials)$P_l^m(x)$の定義には揺れが見られた。具体的には係数$(-1)^m$を球面調和関数の係数として書くのか、ルジャンドル陪多項式の係数として書くのかの２パターンあった。今回使用する計算モジュールは球面調和関数のものであるため係数$(-1)^m$の違いは問題にならないが、ルジャンドル陪多項式の計算モジュールを単独で使用する際には注意が必要である。

特殊関数の定義のされ方の違いについて整理した結果を表2にまとめた。

表2. 特殊関数の定義の違い

以下では、球面調和関数の見かけ上の定義のされ方の違いについて、簡単に見ていきます。

この記事では便宜上、式(1)~(4)で定義される球面調和関数、ルジャンドル陪多項式、ルジャンドル多項式の定義を「真」として、具体的な表式が一致するかを確認しています。式(1)~(4)の定義を「真」とした深い意味はありません。式(1)~(4)以外の定義を「真」としても別に良いと思います。
証明を省略している部分も多いですが何かの手掛かりになれば幸いです。また、何を前提として何を証明しているのかが分かりにくい記述となっているため、論点を明確化し、今後別の記事でまとめるかもしれません。

まず、シッフ、猪木・川合の量子力学の教科書(参考[6,7])では球面調和関数$Y_l^m(\theta, \phi)$は式(1)、(2)のように定義されている。ルジャンドル陪多項式$P_l^m(x)$とルジャンドル多項式$P_l(x)$は式(3)、(4)のように定義されている。球面調和関数$Y_l^m(\theta, \phi)$に対し、$l$、$m$の若い番号のみ具体的に書き下すと式(5)～(7)のようになる。

$$\begin{align} Y_l^m(\theta, \phi) &= \epsilon \sqrt{\frac{2l+1}{4\pi}\cdot \frac{(l-|m|)!}{(l+|m|)!}}P_l^m({\rm cos}\theta)e^{im\phi} \\ \epsilon &= \begin{cases} (-1)^m &(m > 0) \\ 1 &(m \leqq 0)\\ \end{cases}\\ P_l^m(x) &= (1-x^2)^{\frac{|m|}{2}} \frac{d^{|m|}}{dx^{|m|}} P_l(x)\\ P_l(x) &= \frac{1}{2^l l!}\frac{d^l}{dx^l}(x^2-1)^l\\ Y_0^0(\theta, \phi) &= \sqrt{\frac{1}{4\pi}}\\ Y_1^0(\theta, \phi) &= \sqrt{\frac{3}{4\pi}}{\rm cos}\theta\\ Y_1^{\pm 1}(\theta, \phi) &= \mp \sqrt{\frac{3}{8\pi}}{\rm sin}\theta e^{\pm i \phi} \end{align}$$

Scipyの球面調和関数計算モジュールscipy.special.sph_harm(参考[1])での球面調和関数の定義について説明する。scipy.special.sph_harmでは式(8)のように球面調和関数が定義されている。一般的な引数の取り方と$\theta$、$\phi$が逆になっていることに注意されたい。また、ルジャンドル陪多項式$P_l^m(x)$とルジャンドル多項式$P_l(x)$は式(9)、(10)のように定義されている。ここで$(\cdot)_k$はポッホハマー記号(Pochhammer symbol)で、式(11)のように定義される。Scipyでは係数$(-1)^m$をルジャンドル陪多項式の係数として取り扱っている。

$m<0$なる$m$に対し、式(9)は定義不能であるが、$m<0$に対する取り扱い方法はScipyの公式ヘルプには明瞭な形で記載されていなかった。$m<0$に対する動作を正確に把握するにはソースコードを読むか、いくつかの$l, m$に対して動作チェックをする必要がある。一方で、$l, m$の若い番号に対する球面調和関数の具体的な形は式(12)～(14)のような形で記載されており、これは式(5)~(7)と係数含めて一致する。一般的な引数の取り方と$\theta$、$\phi$が逆になっていることに注意すれば、$m<0$なる$m$に対しても式(1)~(4)と同様な定義が球面調和関数に対してなされていると予想される。

以上まとめると、$m<0$なる$m$に対する挙動は若干の不安が残るものの、式(8)~(11)で定義される球面調和関数とルジャンドル多項式は式(1)~(4)で定義されるものと一致すると推定される。一方、式(9)で定義されるルジャンドル陪多項式は式(3)のものと係数$(-1)^m$の分だけ差があることに注意する必要がある。

$$\begin{align} Y_l^m(\theta, \phi) &= \sqrt{\frac{2l+1}{4\pi}\cdot \frac{(l-m)!}{(l+m)!}}P_l^m({\rm cos}\phi)e^{im\theta} \\ P_l^m(x) &= (-1)^m(1-x^2)^{m/2} \frac{d^m}{dx^m} P_l(x)\\ P_l(x) &= \sum_{k=0}^{\infty} \frac{(-l)_k (l+1)_k}{(k!)^2}\left(\frac{1-x}{2}\right)^k\\ (l)_k &= l(l+1)\cdots(l+k-1)\\ Y_0^0(\theta, \phi) &= \sqrt{\frac{1}{4\pi}}\\ Y_1^0(\theta, \phi) &= \sqrt{\frac{3}{4\pi}}{\rm cos}\phi\\ Y_1^{\pm 1}(\theta, \phi) &= \mp \sqrt{\frac{3}{8\pi}}{\rm sin}\phi e^{\pm i \theta} \end{align}$$

式(4)と式(10)で定義されるルジャンドル多項式$P_l(x)$が一致するのかどうかを以下で簡単に補足します。
式(10)では無限級数の形で$P_l(x)$が定義されています。これは一見すると、式(4)と違った式に見えます。ただ、式(10)の無限級数の係数$(-l)_k$は、$k\geq l+1$なる$k$に対し、$(-l)_k=0$であるため有限個の和までで打ち切ることができ、下式が成り立ちます。

$$\sum_{k=0}^{\infty} \frac{(-l)_k (l+1)_k}{(k!)^2}\left(\frac{1-x}{2}\right)^k =\sum_{k=0}^{l} \frac{(-l)_k (l+1)_k}{(k!)^2}\left(\frac{1-x}{2}\right)^k$$

また、下式を上式に代入すると、

$$\begin{align*} (-l)_k &= (-1)^k \cdot l(l-1)(l-2)\cdots(l-k+1) = (-1)^k \frac{l!}{(l-k)!} \\ (l+1)_k &= (l+1)(l+2)\cdots(l+k-1)(l+k) = \frac{(l+k)!}{l!} \end{align*}$$

以下が成立します。

$$\begin{align*} P_l(x) &= \sum_{k=0}^{l} \frac{l!}{k!(l-k)!} \frac{(l+k)!}{k! \cdot l!} (-1)^k\left(\frac{1-x}{2}\right)^k \\ &= \sum_{k=0}^{l} {}_l C_k \cdot {}_{l+k} C_k \left(\frac{x-1}{2}\right)^k \end{align*}$$

これ以上の式変形は省きますが、上式は式(4)と係数含めて一致します。

サクライの量子力学の教科書(参考[8])では球面調和関数$Y_l^m(\theta, \phi)$は式(15)、(16)のように定義されている。ルジャンドル陪多項式$P_l^m(x)$とルジャンドル多項式$P_l(x)$は式(17)、(18)のように定義されている。$m<0$に対する定義の仕方などが、一見すると違って見えるが、よくよく見てみると、式(1)~(4)と同じ定義であることが直ぐに分かる。

$$\begin{align} Y_l^m(\theta, \phi) &= (-1)^m \sqrt{\frac{2l+1}{4\pi}\cdot \frac{(l-m)!}{(l+m)!}}P_l^m({\rm cos}\theta)e^{im\phi}, \ \ \ (m \geqq 0) \\ Y_l^m(\theta, \phi) &= (-1)^{m}Y_l^{m^{\bm *}}(\theta, \phi), \ \ \ (m < 0) \\ P_l^m(x) &= (1-x^2)^{\frac{m}{2}} \frac{d^{m}}{dx^{m}} P_l(x), \ \ \ (m \geqq 0)\\ P_l(x) &= \frac{(-1)^l}{2^l l!}\frac{d^l}{dx^l}(1-x^2)^l = \frac{1}{2^l l!}\frac{d^l}{dx^l}(x^2-1)^l, \ \ \ (m \geqq 0)\\ \end{align}$$

日本語wikipediaで(参考[9])、球面調和関数$Y_l^m(\theta, \phi)$は式(19)のように定義されている。ルジャンドル陪多項式$P_l^m(x)$は式(20)のように定義されている。$\lfloor(l-m)/2 \rfloor$は$(l-m)/2$を超えない最大の整数である。ガウス記号$[\cdot]$を使って定義することもある。ここでは$\lceil \cdot \rceil$と区別するために$\lfloor \cdot \rfloor$が使用されている。式(20)のようにルジャンドル陪多項式を定義すれば、球面調和関数の定義にルジャンドル多項式$P_l(x)$は必要が無いためルジャンドル多項式の定義は記載されていなかった。ただ、$P_l(x)=P_l^0(x)$であるため、式(20)の定義にルジャンドル多項式の定義も含まれていると言えば含まれている。
ここで、$m>0$なる$m$に対し、$\frac{m+|m|}{2}=m$であり、$m\leq0$なる$m$に対し、$\frac{m+|m|}{2}=0$であるから、式(19)の係数は式(1)、(2)の係数と同じものであることが分かる。また、具体的な式変形は省略するが$m\geq0$なる$m$に対し、式(20)と式(3)は係数含めて一致する。よって、式(19)、(20)で定義される球面調和関数、ルジャンドル陪多項式、ルジャンドル多項式は、式(1)～(4)で定義されるものと係数含めて全て一致する。

$$\begin{align} Y_l^m(\theta, \phi) &= (-1)^{\frac{m+|m|}{2}} \sqrt{\frac{2l+1}{4\pi}\cdot \frac{(l-|m|)!}{(l+|m|)!}}P_l^{|m|}({\rm cos}\theta)e^{im\phi} \\ P_l^m(x) &= \frac{1}{2^l}(1-x^2)^{m/2} \sum_{j=0}^{\lfloor(l-m)/2 \rfloor} \frac{(-1)^j(2l-2j)!}{j!(l-j)!(l-2j-m)!}x^{l-2j-m} \end{align}$$

英語wikipedia(参考[10])で、球面調和関数$Y_l^m(\theta, \phi)$は式(21)~(24)のように定義されていた。ルジャンドル陪多項式$P_l^m (x)$とルジャンドル多項式は$P_l (x)$はSpherical harmonicsのページ(参考[10])では定義されていなかったが、Associated Legendre polynomialsのページ(参考[11])で式(23)、(24)のように定義されていた。
式(21)~(24)で定義される球面調和関数$Y_l^m(\theta, \phi)$とルジャンドル多項式$P_l (x)$は式(1)~(4)で定義されるものと係数含めて一致する。一方で、式(23)で定義されるルジャンドル陪多項式$P_l^m (x)$については、係数$(-1)^m$の分だけ式(3)と一致していないので注意が必要である。

$$\begin{align} Y_l^m(\theta, \phi) &= \sqrt{\frac{2l+1}{4\pi}\cdot \frac{(l-m)!}{(l+m)!}}P_l^m({\rm cos}\phi)e^{im\theta} \\ P_l^{-m}(x) &= (-1)^m \frac{(l-m)!}{(l+m)!}P_l^m (x), \ \ \ \ (m>0)\\ P_l^m(x) &= (-1)^m (1-x^2)^{m/2} \frac{d^m}{dx^m}P_l(x) , \ \ \ \ (m\geq0)\\ P_l (x) &= \frac{1}{2^l l!}\frac{d^l}{dx^l}(x^2-1)^l, \ \ \ \ (m\geq0)\\ \end{align}$$

ランダウの教科書(参考[12])では式(25)~(27)のように球面調和関数が定義されていた。これは式(1)~(4)で定義されるものと係数$i^l$だけ異なる。一方、ルジャンドル陪多項式とルジャンドル多項式の定義は式(3),(4)で定義されるものと同じものである。ここで、${\rm sin}^m \theta = (1-{\rm cos}^2 \theta)^{m/2}$を使用し、ランダウの教科書で書かれている表式から若干の変更を加えていることに注意したい。

$$\begin{align} Y_l^m(\theta, \phi) &=i^l \cdot(-1)^{\frac{m+|m|}{2}} \sqrt{\frac{2l+1}{4\pi}\cdot \frac{(l-|m|)!}{(l+|m|)!}}P_l^{|m|}({\rm cos}\theta)e^{im\phi}\\ P_l^m(x) &= (1-x^2)^{m/2} \frac{d^m}{dx^m}P_l(x) , \ \ \ \ (m\geq0)\\ P_l (x) &= \frac{1}{2^l l!}\frac{d^l}{dx^l}(x^2-1)^l, \ \ \ \ (m\geq0)\\ \end{align}$$

ランダウの教科書では一般的な球面調和関数の定義と違い、係数$i^l$の分だけ違った形で定義されていることについて理由を述べています。ランダウによると係数$i^l$をかけた定義の方が、角運動量の合成の観点から見て、最も自然であるとのことです。軌道角運動量だけでなく、スピン角運動量まで考慮した波動関数の時間反転対称性を考えると、式(25)の定義が最も自然であると述べられていました(参考[12,13])。
これについて解説を入れようかと思いましたが、今の私の実力では理解が及びませんでした。私の中で理解・消化できたら記事にしようと思います。

1-2. 球面調和関数計算モジュールを使用上の注意

前節1-1.で球面調和関数の定義を見比べてみたが、scipyでは$Y_l^m(\theta, \phi)$の引数$\theta, \phi$の定義が一般的なものと逆になっている(参考[1])。また$l, m$の順序もデフォルトのままでは間違えやすい。よって、この記事では以下のように関数を定義しなおしている。この方法は参考[14]で紹介されている方法を参考にした。

from scipy.special import sph_harm
def my_sph_harm(l, m, theta, phi):
    return sph_harm(m, l, phi, theta)

2. 球面調和関数の"何の情報"を描画するのが適切か？

水素原子の解を描画しようと思った時のそもそもの興味は、下記の1~3である。ここで、電子波動関数$\Psi_{nlm}(r, \theta, \phi)$と電子確率密度$\rho_{nlm}(r, \theta, \phi)$は、動径波動関数$R_{nl}(r)$と球面調和関数$Y_l^m(\theta, \phi)$を用いて式(28)、(29)のように定義される。1と2はごく自然な動機に思える。3は主に量子化学的動機で、原子単体のことを考える限りは位相のことまで考える意義はあまり感じられないかもしれないが、原子と原子の化学結合を定性的に理解する際に位相の情報が役に立つ。詳細は参考[15-17]などを参考にされたい。

1. 電子波動関数$\Psi_{nlm}(r, \theta, \phi)$の$(x, y, z)$直交空間における分布
2. 電子確率密度$\rho_{nlm}(r, \theta, \phi)$の$(x, y, z)$直交空間における分布
3. 電子波動関数$\Psi_{nlm}(r, \theta, \phi)$の$(x, y, z)$直交空間における位相分布

$$\begin{align} &\Psi_{nlm}(r, \theta, \phi) = R_{nl}(r)Y_l^m(\theta, \phi) \\ &\rho_{nlm}(r, \theta, \phi) = |\Psi_{nlm}(r, \theta, \phi)|^2 = |R_{nl}(r)|^2 |Y_l^m(\theta, \phi)|^2 \end{align}$$

上記の1~3の全ての情報を知るためには動径波動関数$R_{nl}(r)$の項を取り入れる必要があるが、$Y_l^m(\theta, \phi)$の$(x, y, z)$直交空間での位相を含めた分布を調べるだけでも、$\Psi_{nlm}(r, \theta, \phi)$の角度$(\theta, \phi)$方向への位相を含めた広がり方だけは簡易的に見ることができる（電子確率密度$\rho_{nlm}(r, \theta, \phi)$についても同様）。

そこで、本記事では$Y_l^m(\theta, \phi)$に関する位相を含めた情報を$(\theta, \phi)$の直交空間から$(x, y, z)$の直交空間へ情報を落とすことなく完全に射影する方法について説明する。実は、表1で示したPolar PlotsとPolar Plots with Magnitude as Radiusによる図示は、位相の情報を含めて$Y_l^m(\theta, \phi)$に関する情報を$(x, y, z)$の直交空間へと完全に射影できている。

ただ、私たちが高校の化学の教科書(例えば参考[18])や多くの量子化学の教科書で良く見かけるのは、表1で示した実数基底関数を用いたPolar Plots with Magnitude as Radiusによる描画である。本記事ではこの描画方法の利点と他の描画方法の違いについて主に解説する。

1~3の目的に明らかにそぐわないため、本記事では詳しく解説しないが、$(\theta, \phi)$の直交空間で$Y_l^m(\theta, \phi)$を直接描画したのが表1で示した2D polar/azimuthal angle mapによる描画方法である。この描画方法は$(x,y,z)$直交空間上での情報にはなっていないが、$Y_l^m(\theta, \phi)$の情報を位相の情報を含めて完全に有している。

2-1. Polar Plots with Magnitude as Radius

さて、$Y_l^m(\theta, \phi)$に関する情報を$(\theta, \phi)$の直交空間から$(x, y, z)$の直交空間へと射影する方法として、一番最初に思いつくのが式(30)~(32)に示すような変換である。ただし、$\tilde{r}(\theta, \phi)$は0以上の実数である。ここで$r$にチルダをつけて$\tilde{r}$としているのは、動径波動関数$R_{nl}(r)$の引数$r$と区別するためである。

$$\begin{align} x &= \tilde{r}(\theta, \phi) {\rm sin}\theta {\rm cos}\phi \\ y &= \tilde{r}(\theta, \phi) {\rm sin}\theta {\rm sin}\phi \\ z &= \tilde{r}(\theta, \phi) {\rm cos}\theta \\ \end{align}$$

しかしながら、$\tilde{r}(\theta, \phi)$の選び方(定義の仕方)には任意性がある。本来の目的を鑑みると自然に思いつくものは例えば式(33),(34)のような定義の仕方である。それぞれ、$Y_l^m(\theta, \phi)$と$|Y_l^m(\theta, \phi)|^2$の大きさが$(x, y, z)$直交空間における原点からの距離として描画される。式(33)は$Y_l^m(\theta, \phi)$の$(x,y,z)$直交空間での角度$(\theta, \phi)$方向への広がり方、つまり、電子波動関数$\Psi_{nlm}(r, \theta, \phi)$の角度$(\theta, \phi)$方向への広がり方を意識したものである。式(34)は$|Y_l^m(\theta, \phi)|^2$の$(x,y,z)$直交空間での角度$(\theta, \phi$)方向への広がり方、つまり、電子確率密度$\rho_{nlm}(r, \theta, \phi)$の角度$(\theta, \phi$)方向への広がり方を意識したものである。

$$\begin{align} \tilde{r}(\theta, \phi) &= |Y_l^m(\theta, \phi)| \\ \tilde{r}(\theta, \phi) &= |Y_l^m(\theta, \phi)|^2 \\ \end{align}$$

これにより$Y_l^m(\theta, \phi)$の大きさに関する情報は$(x,y,z)$直交空間上へ射影できている。しかし、$Y_l^m(\theta, \phi)$が式(1),(2)のように定義されていたことを思い出すと、下記2点の情報が抜け落ちてしまっている。（下記に改めて式(1),(2)を記した。）

1. 位相$\theta, \phi$によって生じる符号(正負)に関する情報
2. 位相$\phi$によって生じた$e^{im\phi}$が持つ複素空間上での情報

$$\begin{align*} Y_l^m(\theta, \phi) &= \epsilon \sqrt{\frac{2l+1}{4\pi}\cdot \frac{(l-|m|)!}{(l+|m|)!}}P_l^m({\rm cos}\theta)e^{im\phi} \tag{1}\\ \end{align*}$$

$$\begin{align*} \tag{2} \epsilon &= \begin{cases} (-1)^m &(m > 0) \\ 1 &(m \leqq 0)\\ \end{cases}\\ \end{align*}$$

$P_l^m({\rm cos}\theta)$は実数であるため、$|P_l^m({\rm cos}\theta)|$とすることにより失われるのは符号に関する情報だけであるが、$e^{im\phi}$が失う情報はより深刻である。$|e^{im\phi}|=1$であるため、$(x,y,z)$空間への射影で位相$\phi$に関する情報は、以下に示す"色"を使用した表現をしない限り、ほぼ全て失われてしまう。

位相$\theta, \phi$により生じていた1、2の情報を、色空間における色相(参考[19])で表現したのが、表1の複素基底関数系表示によるPolar Plots with Magnitude as Radiusに対応する（改めて図2に抜粋した。表1や図2では式(34)ではなく式(33)の定義を採用し描画している）。ここで、位相$\phi$は$2\pi$ごとに明らかに周期性を持つため、環状の色空間上で描画するのが適切であり、図2ではHSV環状色空間(参考[20])で位相$\theta, \phi$が定義されている。図2の複素基底関数のPolar Plots with Magnitude as Radiusでは$Y_l^m(\theta, \phi)$の持つ情報を完全な形で$(x, y, z)$空間へと射影できている。ただ、位相$\theta, \phi$により生じていた1、2の情報が混ざって表示されてしまっている。また、色による情報が多すぎて位相$\theta, \phi$の情報を視認しにくい。

Twistar48 - Own work, CC BY-SA 4.0, https://onl.tw/BDUDwik
図2. 複素基底関数のPolar Plots with Magnitude as Radius(参考[4]より引用)

これを解決するのが$Y_l^m(\theta, \phi)$の基底変換による実数化である。$\bm Y_l^m(\theta, \phi)$を実数化することで、位相$\phi$の持つ情報を$(x, y, z)$直交空間における形状の情報へと一部変換できる。色による表現を形状による表現に変えることで位相$\phi$の持つ情報の視認性は幾分上がる。具体的な実数への変換方法は式(35)である。ここで、複素数と実数の区別は$m$が上付きか下付きかで区別している。基底変換による実数化の議論は多くの量子化学の教科書で語られているが（例えばザボの量子化学の教科書）(参考[15])、ネット上で読める記事では例えば参考[21]が分かりやすい。実数化した基底関数$Y_{lm}(\theta, \phi)$をPolar Plots with Magnitude as Radiusでプロットしたものが図3である。

$$\begin{align} Y_{lm}(\theta, \phi) = \begin{cases} \frac{i}{\sqrt 2}\left(Y_l^{-|m|}(\theta, \phi) + (-1)^{|m|+1} \cdot Y_l^{|m|}(\theta, \phi) \right) & (m<0)\\ Y_l^{m}(\theta, \phi) & (m = 0)\\ \frac{1}{\sqrt 2}\left(Y_l^{-m}(\theta, \phi) + (-1)^{m} \cdot Y_l^{m}(\theta, \phi) \right) & (m>0) \end{cases}\\ \end{align}$$

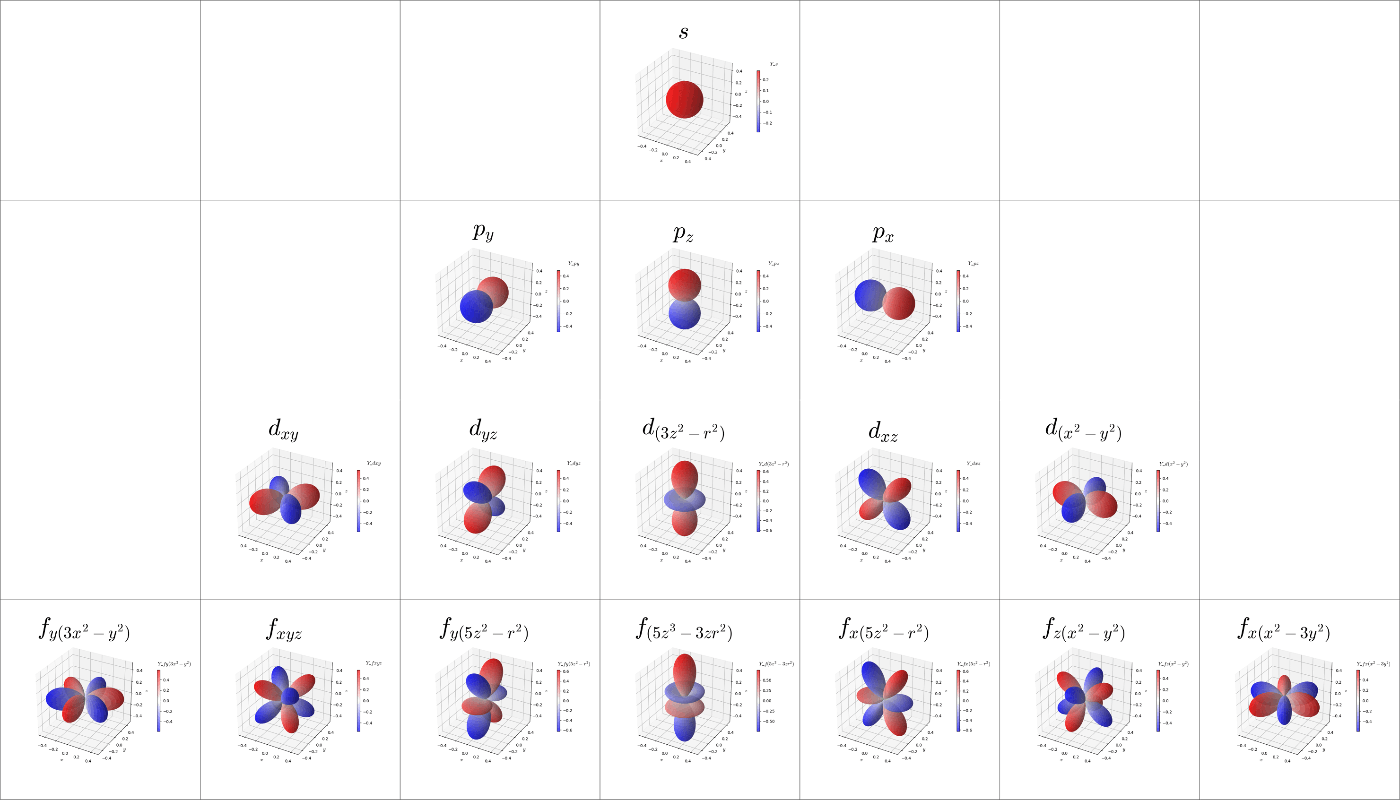
図3. 実数化した基底関数のPolar Plots with Magnitude as Radius

式(35)による基底変換は、複素基底関数系$\left\{Y_l^m(\theta, \phi)\right\}$が備えていた重要な性質である正規直交性を、実数基底関数系$\left\{Y_{lm}(\theta, \phi)\right\}$へと遺伝させることができている点に注意したい。

複素基底関数系$\left\{Y_l^m(\theta, \phi)\right\}$は正規直交性を持ち、式(a)が成り立ちます。実数基底関数系$\left\{Y_{lm}(\theta, \phi)\right\}$が正規直交性を持っているかは、式(b)を示せば良いですが、式(b)は式(a)と式(35)から直ぐに導けます。気になった方は確認してみても良いかもしれません。

$$\int_0^{2\pi}d\phi \int_0^{\pi} (Y_l^m)^{*}(\theta, \phi)Y_{l'}^{m'}(\theta, \phi) {\rm sin}\theta d\theta = \delta_{ll'} \delta_{mm'} \tag{a}$$

$$\int_0^{2\pi}d\phi \int_0^{\pi} (Y_{lm})^{*}(\theta, \phi)Y_{l'm'}(\theta, \phi) {\rm sin}\theta d\theta = \delta_{ll'} \delta_{mm'} \tag{b}$$

図3では式(36)のように$\tilde{r}(\theta, \phi)$を定義し、式(30)~(32)のような射影をしている。このとき、式(36),(37)のどちらの定義を採用するかは、電子波動関数$\Psi_{nlm}(r, \theta, \phi)$と電子確率密度$\rho_{nlm}(r, \theta, \phi)$のどちらを意識するかの違いであって、目的に応じて使い分ける必要がある。複素基底関数系$\left\{Y_l^m(\theta, \phi)\right\}$による表現では、色付けによる表現を取らない限り、①$Y_l^m(\theta, \phi)$の符号に関する情報、②$e^{im\phi}$が持つ複素空間上での情報の二つが失われていた。一方、実数基底関数系$\left\{Y_{lm}(\theta, \phi)\right\}$による表現で失われる情報は、$Y_{lm}(\theta, \phi)$の符号に関する情報のみである。そこで、図3では、$\bm Y_{lm}(\theta, \phi)$が本来持っていた情報を完全な形で$(x,y,z)$空間へと射影するために、$\bm Y_{lm}(\theta, \phi)$の符号に応じて、色付けをしている。これにより、$Y_{lm}(\theta, \phi)$の持つ情報を完全な形で$(x,y,z)$空間へと射影できる。

$$\begin{align} \tilde{r}(\theta, \phi) &= |Y_{lm}(\theta, \phi)| \\ \tilde{r}(\theta, \phi) &= |Y_{lm}(\theta, \phi)|^2 \\ \end{align}$$

$Y_l^m(\theta, \phi)$を$Y_{lm}(\theta, \phi)$へと実数化すると、位相$\phi$の持つ情報は$(x, y, z)$空間における形状の情報へと変換され、位相$\phi$の情報は視認しやすくなった。一方で、$Y_{lm}(\theta, \phi)$へと実数化することで失った情報もある。それは、$Y_l^m(\theta, \phi)$からなる基底関数系は、すべての整数$l,m(l\geq0)$に対し、z軸方向の軌道角運動量$\hat{L}_z$(式(38))の固有関数であったが、実数化に伴う基底変換で$m=0$なる$m$を除き、$Y_{lm}(\theta, \phi)$は固有関数ではなくなってしまっているということである。

つまり、図3のような実数基底関数系による表現は、z軸方向の軌道角運動量$\hat{L}_z$の固有関数であることを諦めた一方で、位相$\phi$の視認性を強く意識した描画であるとも言える。私たちが図3のような実数基底関数系による図示をよく見かけるのは、複素基底関数系による図示(図2)ではカラー印刷が必須であり印刷費がかさむことに加えて、位相$\phi$の視認性を上げたいことが理由であると推定される。（おそらくこれ以上の合理的理由は無い。）

$$\begin{align} \hat{L}_z = -i \hbar \frac{\partial}{\partial \phi} \end{align}$$

上記で、実数化された基底関数では、z軸方向の軌道角運動量$\hat{L}_z$の固有関数であることを"諦めた"、というネガティブな表現を使いましたが、これはz軸方向を特別な方向として見ることを辞めた、とポジティブに考えることもできます。中心力ポテンシャル$V(r)$を持つシュレディンガー方程式は、空間に対して等方的であるため、$\hat{L}_z$のみの固有関数であることは本来奇妙です。ただ、実数化された基底関数は下記のように$\hat{L}_z$のみの固有関数となっているわけではないことが、簡単な計算から確認できます。

$$\hat{L}_x Y_{11}(\theta, \phi) = 0 \cdot Y_{11}(\theta, \phi) \\ \hat{L}_z Y_{10}(\theta, \phi) = 0 \cdot Y_{10}(\theta, \phi) \\ \hat{L}_y Y_{1,-1}(\theta, \phi) = 0 \cdot Y_{1,-1}(\theta, \phi) \\$$

一方、実数化された基底関数$Y_{lm}(\theta, \phi)$が、一般の$l,m$に対し、どういった演算子の固有関数になっているのかを示すのは難しく、私はそこまで示せませんでした。もしかすると、そういった演算子は存在しないのかもしれません。実際、私が確認した資料(参考6-8,12,13,22)ではそこまで語られていませんでした。

勿論、$Y_{lm}(\theta, \phi)$はr方向の運動量演算子$\hat{p}_r$と全軌道角運動量の2乗の演算子$\hat{L}^2$の固有関数になっていることは、$Y_{lm}(\theta, \phi)$が$r$に依存しない関数であることと、下式と式(35)から確認できます。これ以上の情報をお持ちの方がいらっしゃいましたらコメント欄、もしくはTwitterのメッセージなどで教えて貰えると幸いです。

$$\hat{p}_r = -i \hbar \left( \frac{\partial}{\partial r} + \frac{1}{r} \right)\\ \hat{L}^2 Y_l^m (\theta, \phi) = l(l+1)\hbar^2 Y_l^m (\theta, \phi)$$

2-2. Polar Plots

2-1.節で、$Y_{l}^m(\theta, \phi)$や$Y_{lm}(\theta, \phi)$の情報を式(30)~(32)を使って(x,y,z)直交空間へと射影する方法について説明した。このとき、$\tilde{r}(\theta, \phi)$として、式(33),(34),(36),(37)のように定義した。ただ、$\tilde{r}(\theta, \phi)$の定義には任意性があり、式(39)のように定義することもできる。これが表1中のPolar Plotsによる描画である。このとき式(39)中には$Y_{l}^m(\theta, \phi)$や$Y_{lm}(\theta, \phi)$の情報が一切入っていないため、Polar Plotsでは$Y_{l}^m(\theta, \phi)$や$Y_{lm}(\theta, \phi)$の情報を色で表現している。

$Y_{l}^m(\theta, \phi)$や$Y_{lm}(\theta, \phi)$の大きさを彩度(参考[19])で表現し、$Y_{l}^m(\theta, \phi)$や$Y_{lm}(\theta, \phi)$の位相を色相(参考[19])で表現している。これにより、$Y_{l}^m(\theta, \phi)$や$Y_{lm}(\theta, \phi)$の持つ情報を完全な形で(x,y,z)直交空間へ射影できているが、余りにも色に持たせる情報が多すぎて視認性が悪いため、量子力学や量子化学の分野でこの描画方法を採用することはあまりない。

$$\begin{align*} \tilde{r}(\theta, \phi) &= |Y_l^m(\theta, \phi)| \tag{33} \end{align*}$$

$$\begin{align*} \tilde{r}(\theta, \phi) &= |Y_l^m(\theta, \phi)|^2 \tag{34}\\ \end{align*}$$

$$\begin{align*} \tilde{r}(\theta, \phi) &= |Y_{lm}(\theta, \phi)| \tag{36}\\ \end{align*}$$

$$\begin{align*} \tilde{r}(\theta, \phi) &= |Y_{lm}(\theta, \phi)|^2 \tag{37}\\ \end{align*}$$

$$\begin{align} \tilde{r}(\theta, \phi) &= 1\\ \end{align}$$

3. matplotlibでの描画：カラープロット

ここでは、2-1.節で説明したPolar Plots with Magnitude as Radiusの描画方法について説明する。0.節で触れたようにmatplotlibで球面調和関数の描画をしようとすると、球面調和関数の位相による色分けがデフォルトの機能だけではできない(図1再掲)。

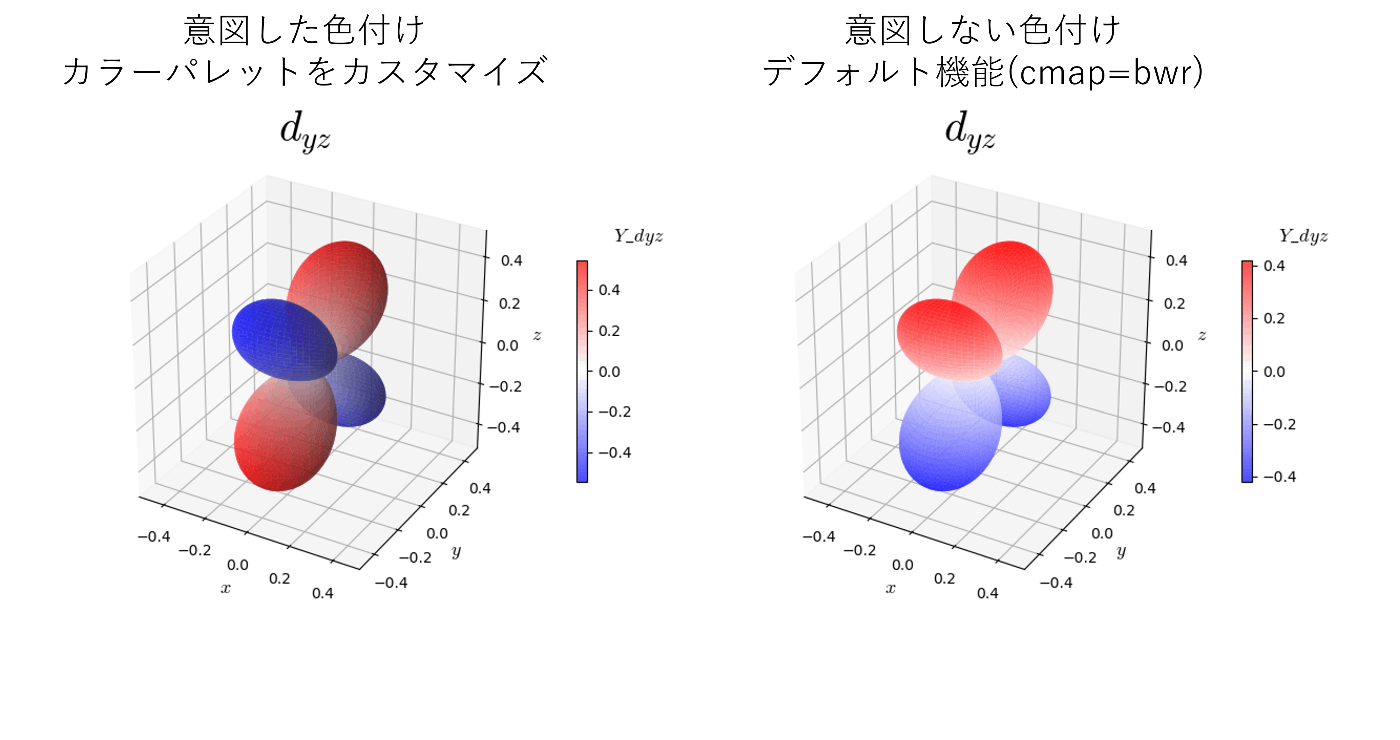
図1. 球面調和関数の意図した色付けと意図しない色付け(再掲)

そこで今回は下記に示すようなコードで目的を達成した。球面調和関数を実数化し、色分けが2値化で十分な場合は、参考[21]で記載されているような方法で十分に目的は達成できる。今回は他の目的にも応用できるように連続的な色付けができる方法をとった。この方法は参考[5,23]の記事を参考にした。このとき、カラーバーとplot_surfaceで別々に色の制御を行っていることに注意したい。このコードでは実数化された球面調和関数Yの値に依存した色分けがなされる。bwrのカラーパレットを使用した場合は図4のような色付けがなされ、jetのカラーパレットを使用した場合は図5のような色付けがなされる。

import matplotlib
import matplotlib.pyplot as plt
import matplotlib.cm as cm

"""
~~~ 中略 ~~~
"""

# --- グラフ基本設定 ---
fig = plt.figure(figsize=(7,7))
ax = fig.add_subplot(1,1,1, projection='3d')
ax.set_box_aspect((1, 1, 1))

# 色の設定
alpha = 0.7    #　透明度
color = cm.bwr #　色: blue, white, red
#color = cm.jet #　色：虹色のパレットを使用したい場合
    
# 色の正規化オブジェクト：norm
Max = np.maximum( np.fabs(np.amin(Y)), np.fabs(np.amax(Y)))
norm = matplotlib.colors.Normalize(vmin = -Max, vmax = Max)
    
# カラーバーの設定
m = cm.ScalarMappable(cmap=color, norm=norm)
cbar = fig.colorbar(m, alpha=alpha, shrink=0.4, pad=0.1)
cbar.set_label(Y_name, rotation=0, y=1.15)

ax.plot_surface(x, y, z, facecolors=color(norm(Y)) , alpha = alpha, linewidth=0, rstride=rst, cstride=cst)

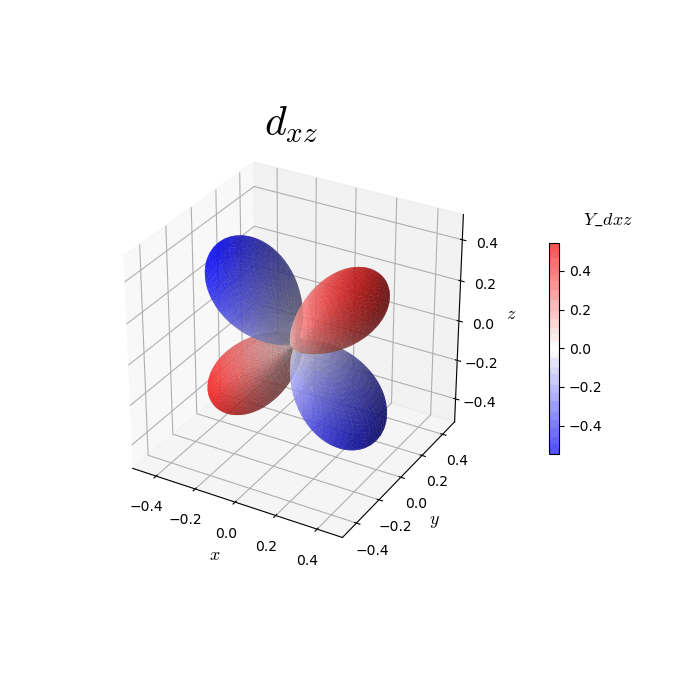
図4. bwrのカラーパレットを使用した場合の色付け

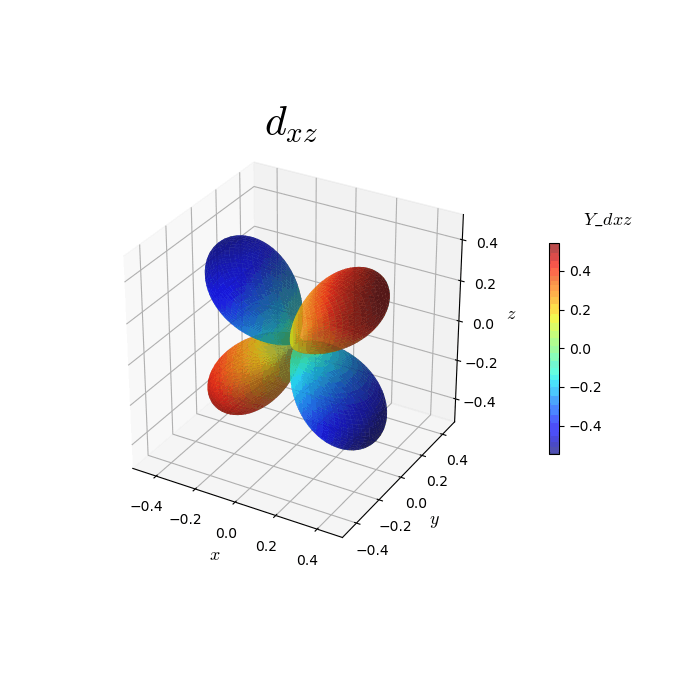
図5. jetのカラーパレットを使用した場合の色付け

下記は方位量子数$l$と磁気量子数$m$を指定することで実数化された球面調和関数を描画するためのサンプルコードである。方位量子数$l$と磁気量子数$m$を指定することで１枚のグラフが生成される。scipyの球面調和関数計算モジュールscipy.special.sph_harmを使用しているため、任意の方位量子数$l$と磁気量子数$m$に対し、グラフを生成できる。また、$\tilde{r}(\theta, \phi)$として、式(36)と式(37)のどちらの定義を採用するかはコメントで入れ替えられるようにしているので、適宜入れ替えて利用されたい。

$$\begin{align*} \tilde{r}(\theta, \phi) &= |Y_{lm}(\theta, \phi)| \tag{36}\\ \end{align*}$$

$$\begin{align*} \tilde{r}(\theta, \phi) &= |Y_{lm}(\theta, \phi)|^2 \tag{37}\\ \end{align*}$$

単一のグラフ作成

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from scipy.special import sph_harm

# カラーバーラベル、グラフタイトルを選択するための関数
def select_name(l, m):
    # グラフ描画用リスト: s~f (l = 0, 1, 2, 3)
    Y_name = \
    ["$Y\_s$", \
     "$Y\_py$", "$Y\_pz$", "$Y\_px$", \
     "$Y\_dxy$", "$Y\_dyz$", "$Y\_d(3z^2-r^2)$", "$Y\_dxz$", "$Y\_d(x^2-y^2)$", \
     "$Y\_fy(3x^2-y^2)$", "$Y\_fxyz$", "$Y\_fy(5z^2-r^2)$", "$Y\_f(5z^3-3zr^2)$", \
     "$Y\_fx(5z^2-r^2)$", "$Y\_fz(x^2-y^2)$", "$Y\_fx(x^2-3y^2)$"]

    orbit_name = \
    ["$s$", \
     "$p_y$", "$p_z$", "$p_x$", \
     "$d_{xy}$", "$d_{yz}$", "$d_{(3z^2-r^2)}$", "$d_{xz}$", "$d_{(x^2-y^2)}$", \
     "$f_{y(3x^2-y^2)}$", "$f_{xyz}$", "$f_{y(5z^2-r^2)}$", "$f_{(5z^3-3zr^2)}$", \
     "$f_{x(5z^2-r^2)}$", "$f_{z(x^2-y^2)}$", "$f_{x(x^2-3y^2)}$"]

    # l_maxが4より大きい場合はY_nameとtitle_nameに空の名前を追加
    if l >= 4:
        Y_name.append("")
        orbit_name.append("")
        
    # Y_name, title_nameのインデックスの選択
    if l <= 3:
        i=-1
        for p in range(0, l+1, 1):
            for q in range(-p, p+1, 1):
                
                if p != l or q<= m:
                    i = i+1
    else:
        i = 16 
    
    return Y_name[i], orbit_name[i]


# 球面調和関数のノーテーションや文字を物理の教科書用にカスタマイズ
def my_sph_harm(l, m, theta, phi):
    return sph_harm(m, l, phi, theta)

# 実数化した球面調和関数を算出する関数：関数の中でmy_sph_harm()使用
def real_sph_harm(l, m, theta, phi):
    
    if m < 0:
        # m < 0であることに注意: np.fabs(m) = -m
        Y = np.real(1.j * np.sqrt(1/2) * (my_sph_harm(l,m, theta, phi) + (-1)**(-m+1) * my_sph_harm(l, -m, theta, phi)))
    if m == 0:
        Y = np.real(my_sph_harm(l, m, theta, phi))
    if m > 0:
        Y = np.real(np.sqrt(1/2) * (my_sph_harm(l,-m, theta, phi) + (-1)**m * my_sph_harm(l, m, theta, phi)))
    
    return Y

# (r,Θ,φ)空間から(x,y,z)空間への射影
def polar(r, theta, phi):
    x = r * np.sin(theta) * np.cos(phi)
    y = r * np.sin(theta) * np.sin(phi)
    z = r * np.cos(theta)
    return x, y, z

# グラフの描画用の関数
def plot_surf(x, y, z, Y, Y_name, title_name, filename, l, m, ax_lim, rst, cst):
    
    # --- グラフ基本設定 ---
    plt.rcParams["xtick.labelsize"] = 10        # 目盛りのフォントサイズ
    plt.rcParams["ytick.labelsize"] = 10        # 目盛りのフォントサイズ
    plt.rcParams["axes.labelsize"] = 13         # 軸ラベルのフォントサイズ
    plt.rcParams["axes.titlesize"] = 30         # グラフタイトルのフォントサイズ
    plt.rcParams["mathtext.fontset"] = "cm"     # TeXのフォント, デフォルト:dejavusans
    plt.rcParams["figure.dpi"] = 100            # dpi(dots per inch):解像度
    fig = plt.figure(figsize=(7,7))
    ax = fig.add_subplot(1,1,1, projection='3d')
    ax.set_box_aspect((1, 1, 1))
    
    # 色の設定
    alpha = 0.7    #　透明度
    color = cm.bwr #　色: blue, white, red
    #color = cm.jet # 色：　虹色
    
    # 色の正規化オブジェクト：norm
    Max = np.maximum( np.fabs(np.amin(Y)), np.fabs(np.amax(Y)))
    norm = matplotlib.colors.Normalize(vmin = -Max, vmax = Max)
    
    # カラーバーの設定
    m = cm.ScalarMappable(cmap=color, norm=norm)
    cbar = fig.colorbar(m, alpha=alpha, shrink=0.4, pad=0.1)
    cbar.set_label(Y_name, rotation=0, y=1.15)
    
    # サーフェスプロット
    if l == 0 and m ==0 :
        # --- 例外処理をしている理由 ---
        # l==0 and m==0 はs軌道のとき
        # s軌道は球面調和関数の大きさが常に一定なのでbwrのパレットを使用すると真っ白な球になってしまう
        # norm(Y)が -MaxとMaxの中点0になる
        # 実数化球面調和関数が正の値を持つときは赤い色付けをしたいため、例外処理を行っている
        ax.plot_surface(x, y, z, color="red" , alpha = alpha, linewidth=0, rstride=rst, cstride=cst)
    else:
        ax.plot_surface(x, y, z, facecolors=color(norm(Y)) , alpha = alpha, linewidth=0, rstride=rst, cstride=cst)
    
    # 軸範囲、ラベル、グラフタイトル
    ax.set_xlim(-ax_lim, ax_lim)
    ax.set_ylim(-ax_lim, ax_lim)
    ax.set_zlim(-ax_lim, ax_lim)
    ax.set_xlabel('$x$')
    ax.set_ylabel('$y$')
    ax.set_zlabel('$z$')
    ax.set_title(title_name)
    
    # 図の保存
    fig.savefig(filename)
    
    plt.show()
    plt.close()
    
    return 0

# -----------   Input Parameter  ---------------------------------------------
l      = 2    #　方位量子数, 0以上の整数値
m      = 1    # 磁気量子数, -l<= m <=l を満たす整数
ax_lim = 0.5  #　グラフの描画範囲
rst    = 1    #　rstride:プロットのサンプリング間隔, 推奨値は1~3
cst    = 1    # cstride:プロットのサンプリング間隔, 推奨値は1~3
N      = 101  # theta, phiの分割数, 0以上の整数値
filename = "好きな名前" #保存する図の名前 

# -------------  補足 ---------------------------------------------------------
# m     : -l<= m <=l を満たす整数が指定されていない場合は多分エラーになる。
# ax_lim: グラフの描画範囲が狭いと感じたらこれを大きくとること
# l に4以上を指定した場合はグラフタイトル、カラーバーのラベルが表示されない。グラフ描画自体はできる。

# ------------- 計算が遅いと感じたときにすること ----------------------------------------
# グラフの描画が計算速度のボトルネックになっている。
# rst, cstを大きくとることで計算速度は速くなる。
# ただし、rst, cstを大きくするとがグラフは粗くなる。
# rst, cstの推奨値は1~3。これ以上大きくとるとグラフが粗くなりすぎる。


# theta, phi: 定義域設定
theta_min = 0.0
theta_max = np.pi
phi_min = 0.0
phi_max = 2.0 * np.pi

# theta, phi: メッシュ作成
theta_a = np.linspace(theta_min, theta_max, N)
phi_a = np.linspace(phi_min, phi_max, N)
theta, phi = np.meshgrid(theta_a, phi_a)

# 計算
Y_real = real_sph_harm(l, m, theta, phi)
#r_tilde = Y_real**2
r_tilde = np.fabs(Y_real)
x, y, z = polar(r_tilde, theta, phi)

# カラーバーラベルとタイトルネームの取得
Y_name, title_name = select_name(l, m)
# グラフ描画
plot_surf(x, y, z, Y_real, Y_name, title_name, filename, l, m, ax_lim, rst, cst)

下記はl_maxで与えた方位量子数に対し、0<= l <=l_maxを満たすような方位量子数$l$とそれに対応した全ての磁気量子数$m$のグラフを生成するコードである。コードの中身自体は上記のコードとほぼ同じものなので記事としては折り畳んで表示する。合計で(l_max+1)**2個のグラフが生成されるのでl_maxに大きな値を入れすぎると大量のグラフが生成されてしまうので注意されたい。

複数のグラフを同時生成するサンプルコード

複数のグラフを同時生成

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from scipy.special import sph_harm

# 球面調和関数のノーテーションや文字を物理の教科書用にカスタマイズ
def my_sph_harm(l, m, theta, phi):
    return sph_harm(m, l, phi, theta)

# 実数化した球面調和関数を算出する関数：関数の中でmy_sph_harm()使用
def real_sph_harm(l, m, theta, phi):
    
    if m < 0:
        # m < 0であることに注意: np.fabs(m) = -m
        Y = np.real(1.j * np.sqrt(1/2) * (my_sph_harm(l,m, theta, phi) + (-1)**(-m+1) * my_sph_harm(l, -m, theta, phi)))
    if m == 0:
        Y = np.real(my_sph_harm(l, m, theta, phi))
    if m > 0:
        Y = np.real(np.sqrt(1/2) * (my_sph_harm(l,-m, theta, phi) + (-1)**m * my_sph_harm(l, m, theta, phi)))
    
    return Y

# (r,Θ,φ)空間から(x,y,z)空間への射影
def polar(r, theta, phi):
    x = r * np.sin(theta) * np.cos(phi)
    y = r * np.sin(theta) * np.sin(phi)
    z = r * np.cos(theta)
    return x, y, z

# グラフの描画用の関数
def plot_surf(x, y, z, Y, Y_name, graph_name, i, ax_lim, rst, cst):
    
    # --- グラフ基本設定 ---
    plt.rcParams["xtick.labelsize"] = 10        # 目盛りのフォントサイズ
    plt.rcParams["ytick.labelsize"] = 10        # 目盛りのフォントサイズ
    plt.rcParams["axes.labelsize"] = 13         # 軸ラベルのフォントサイズ
    plt.rcParams["axes.titlesize"] = 30         # グラフタイトルのフォントサイズ
    plt.rcParams["mathtext.fontset"] = "cm"     # TeXのフォント, デフォルト:dejavusans
    plt.rcParams["figure.dpi"] = 100            # dpi(dots per inch):解像度
    fig = plt.figure(figsize=(7,7))
    ax = fig.add_subplot(1,1,1, projection='3d')
    ax.set_box_aspect((1, 1, 1))
    
    # 色の設定
    alpha = 0.7    #　透明度
    color = cm.bwr #　色: blue, white, red
    
    # 色の正規化オブジェクト：norm
    Max = np.maximum( np.fabs(np.amin(Y)), np.fabs(np.amax(Y)))
    norm = matplotlib.colors.Normalize(vmin = -Max, vmax = Max)
    
    # カラーバーの設定
    m = cm.ScalarMappable(cmap=color, norm=norm)
    cbar = fig.colorbar(m, alpha=alpha, shrink=0.4, pad=0.1)
    cbar.set_label(Y_name, rotation=0, y=1.15)
    
    # サーフェスプロット
    if Y_name == "$Y\_s$" :
        # --- 例外処理をしている理由 ---
        # s軌道は球面調和関数の大きさが常に一定なのでbwrのパレットを使用すると真っ白な球になってしまう
        # norm(Y)が -MaxとMaxの中点0になる
        # 実数化球面調和関数が正の値を持つときは赤い色付けをしたいため、例外処理を行っている
        ax.plot_surface(x, y, z, color="red" , alpha = alpha, linewidth=0, rstride=rst, cstride=cst)
    else:
        ax.plot_surface(x, y, z, facecolors=color(norm(Y)) , alpha = alpha, linewidth=0, rstride=rst, cstride=cst)
    
    # 軸範囲、ラベル、グラフタイトル
    ax.set_xlim(-ax_lim, ax_lim)
    ax.set_ylim(-ax_lim, ax_lim)
    ax.set_zlim(-ax_lim, ax_lim)
    ax.set_xlabel('$x$')
    ax.set_ylabel('$y$')
    ax.set_zlabel('$z$')
    ax.set_title(graph_name)
    
    # 図の保存
    name = graph_name.replace('$', '')   # 文字列から $ を除去
    name = name.replace('{', '')         # 文字列から { を除去
    name = name.replace('}', '')         # 文字列から } を除去
    if i <= 15:
        # 0<= i <=15 : s~f軌道        
        fig.savefig(name)
    else:
        # 16 <= i: g軌道以降
        filename = "Orbit_"
        filename = filename + str(i)
        fig.savefig(filename)
    
    plt.show()
    plt.close()
    
    return 0

# -----------   Input Parameter  ---------------------------------------------
l_max  = 3    #　方位量子数lの最大値, 0以上の整数値
r_flag = 1    # 0 なら実数化球面調和関数の2乗が半径、1 なら実数化球面調和関数の絶対値が半径
ax_lim = 0.5  #　グラフの描画範囲。r_flag=0 なら0.3程度、r_flag=0 なら0.5程度の値が良い
rst    = 1    #　rstride:プロットのサンプリング間隔, 推奨値は1~3
cst    = 1    # cstride:プロットのサンプリング間隔, 推奨値は1~3
N      = 101  # theta, phiの分割数, 0以上の整数値

# -------------  補足 ---------------------------------------------------------
# l_max : 最も重要なインプット
# r_flag: 0 か 1 以外の値が指定されると実数化球面調和関数の2乗が半径になる。
# ax_lim: グラフの描画範囲が狭いと感じたらこれを大きくとること
# (l_max + 1)**2 個のグラフが出力される。
# l_max に4以上を指定した場合はグラフタイトル、カラーバーのラベルが表示されない。グラフ描画自体はできる。
# l_max にあまりに巨大な数を入力すると画像が大量生成されて大変なことになる。
# l_max=4 で25個のグラフ、l_max=5 で36個のグラフが生成される。

# ------------- 計算が遅いと感じたときにすること ----------------------------------------
# グラフの描画が計算速度のボトルネックになっている。
# rst, cstを大きくとることで計算速度は速くなる。
# ただし、rst, cstを大きくするとがグラフは粗くなる。
# rst, cstの推奨値は1~3。これ以上大きくとるとグラフが粗くなりすぎる。


# theta, phi: 定義域設定
theta_min = 0.0
theta_max = np.pi
phi_min = 0.0
phi_max = 2.0 * np.pi

# theta, phi: メッシュ作成
theta_a = np.linspace(theta_min, theta_max, N)
phi_a = np.linspace(phi_min, phi_max, N)
theta, phi = np.meshgrid(theta_a, phi_a)


# グラフ描画用リスト: s~f (l = 0, 1, 2, 3)
Y_name = \
["$Y\_s$", \
 "$Y\_py$", "$Y\_pz$", "$Y\_px$", \
 "$Y\_dxy$", "$Y\_dyz$", "$Y\_d(3z^2-r^2)$", "$Y\_dxz$", "$Y\_d(x^2-y^2)$", \
 "$Y\_fy(3x^2-y^2)$", "$Y\_fxyz$", "$Y\_fy(5z^2-r^2)$", "$Y\_f(5z^3-3zr^2)$", \
 "$Y\_fx(5z^2-r^2)$", "$Y\_fz(x^2-y^2)$", "$Y\_fx(x^2-3y^2)$"]

graph_name = \
["$s$", \
 "$p_y$", "$p_z$", "$p_x$", \
 "$d_{xy}$", "$d_{yz}$", "$d_{(3z^2-r^2)}$", "$d_{xz}$", "$d_{(x^2-y^2)}$", \
 "$f_{y(3x^2-y^2)}$", "$f_{xyz}$", "$f_{y(5z^2-r^2)}$", "$f_{(5z^3-3zr^2)}$", \
 "$f_{x(5z^2-r^2)}$", "$f_{z(x^2-y^2)}$", "$f_{x(x^2-3y^2)}$"]

# l_maxが4より大きい場合はY_nameとgraph_nameに空の名前を追加
if l_max >= 4:
    for i in range(16, (l_max+1)**2+1, 1):
        Y_name.append("")
        graph_name.append("")
    
    
i = 0 # Y_name, graph_nameのインデックス

for l in range(0, l_max+1, 1):
    for m in range(-l, l+1, 1):
        
        Y_real = real_sph_harm(l, m, theta, phi)
        
        if r_flag == 0 or r_flag != 1:
            r_tilde = Y_real**2
        elif r_flag == 1:
            r_tilde = np.fabs(Y_real)
        
        x, y, z = polar(r_tilde, theta, phi)
        plot_surf(x, y, z, Y_real,  Y_name[i], graph_name[i], i, ax_lim, rst, cst)
        
        i = i + 1

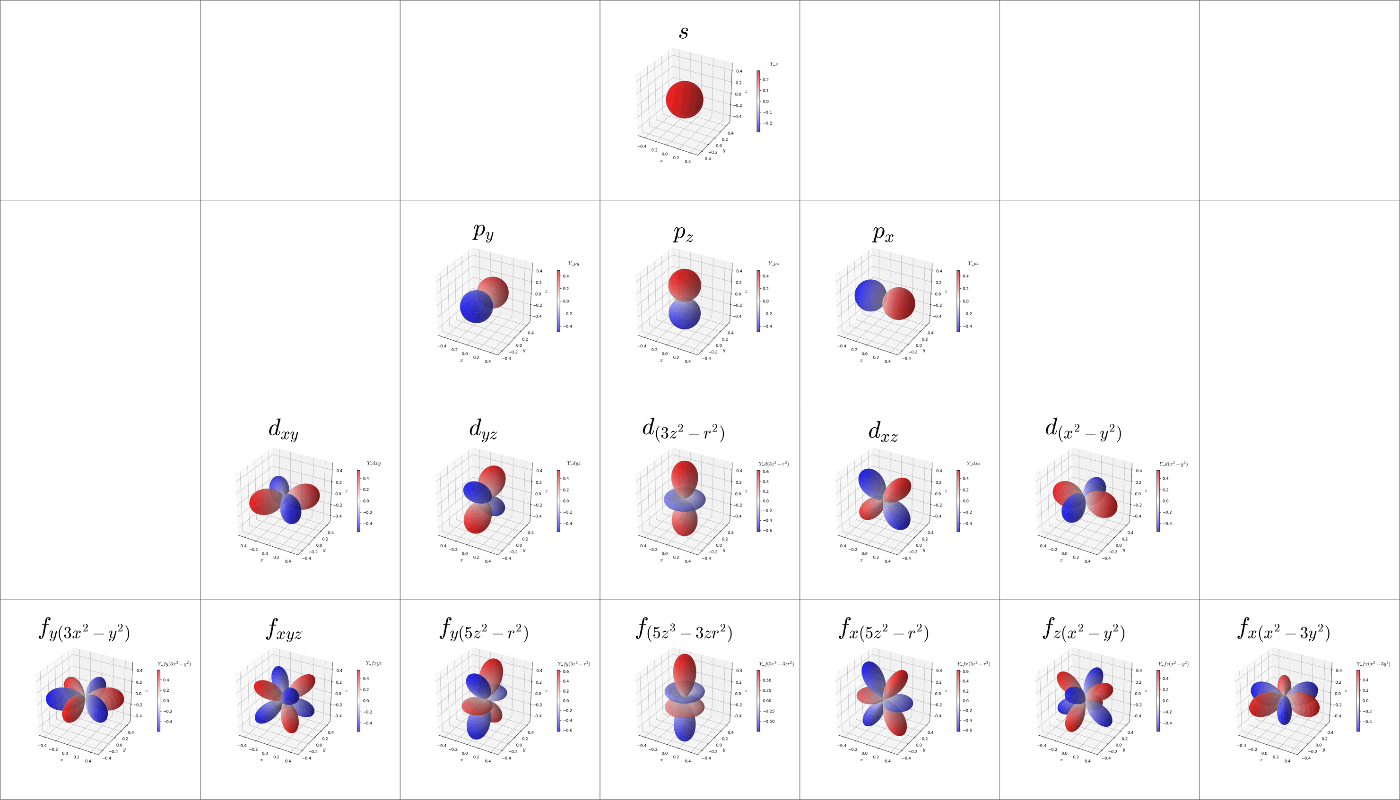
このコードを使用して描いたs~f軌道のグラフを図6,7に示す。他の方が書かれた記事で掲載されていもの(参考[21,24])と同等のグラフが得られており、問題なくプログラムを作成できていることが確認できた。図6は式(36)の定義を採用して描いたグラフで、図7は式(37)の定義を採用して描いたグラフである。軌道の命名規則は分かりにくいが参考[25]の'Real spherical harmonics'の項を参考にした。

$$\begin{align*} \tilde{r}(\theta, \phi) &= |Y_{lm}(\theta, \phi)| \tag{36}\\ \end{align*}$$

$$\begin{align*} \tilde{r}(\theta, \phi) &= |Y_{lm}(\theta, \phi)|^2 \tag{37}\\ \end{align*}$$

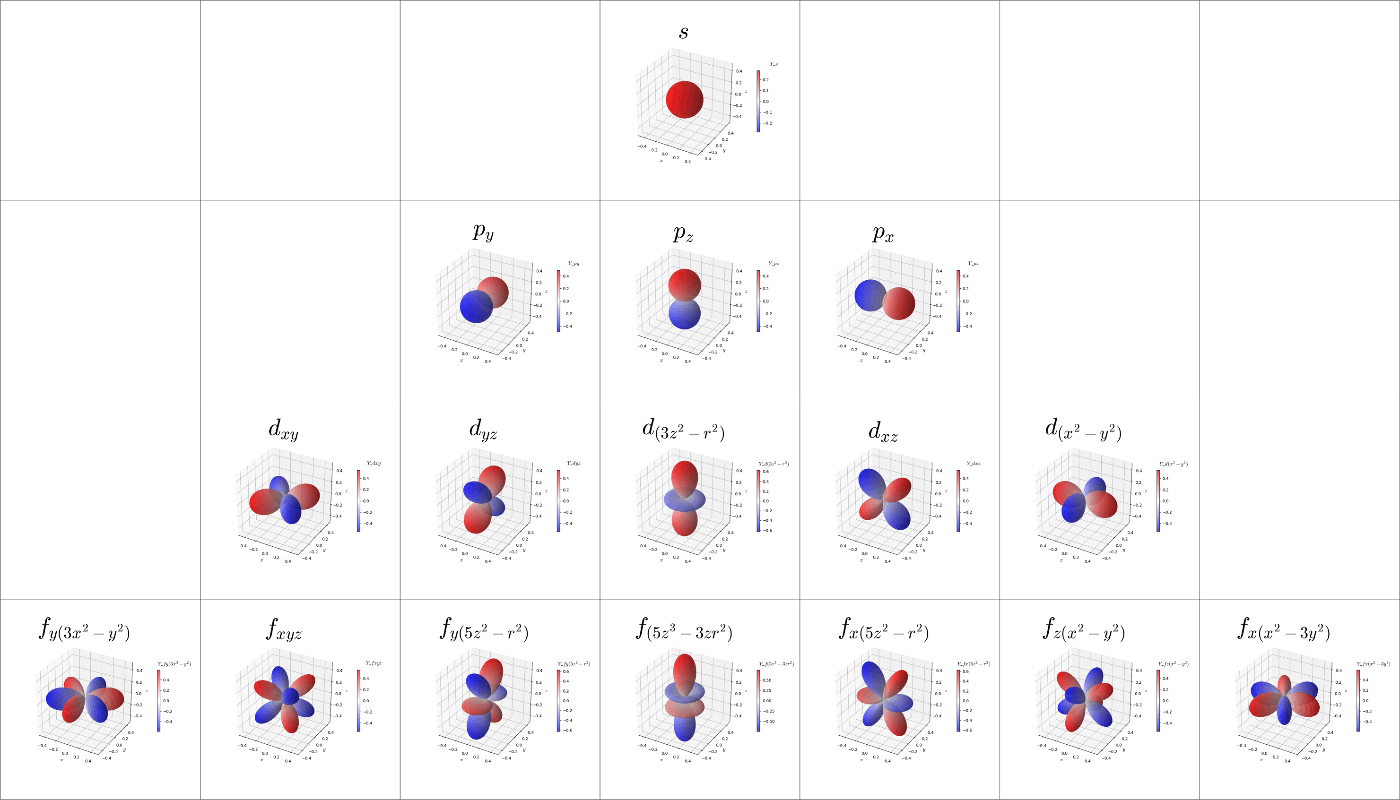
図6. 実数化された球面調和関数：$\tilde{r}(\theta, \phi) = |Y_{lm}(\theta, \phi)|$

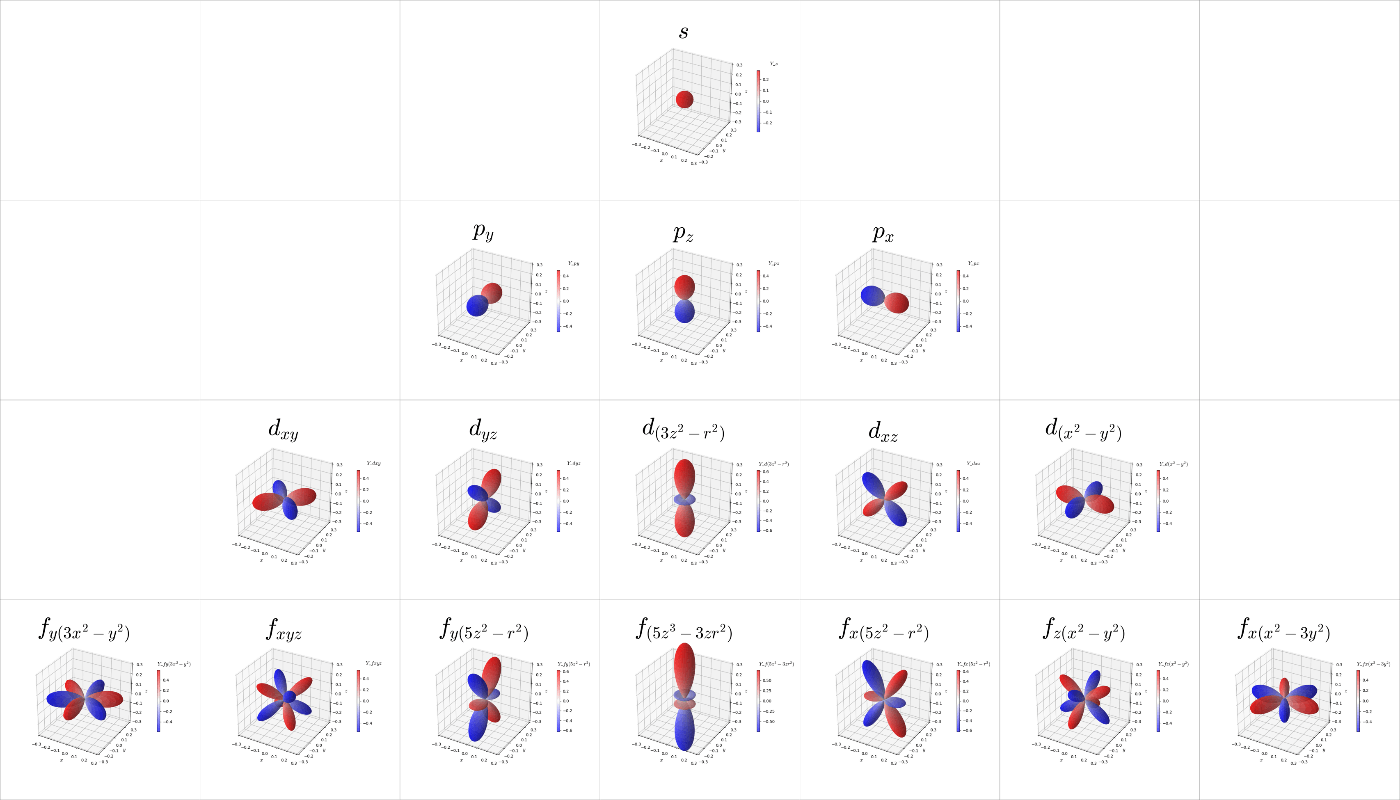
図7. 実数化された球面調和関数：$\tilde{r}(\theta, \phi) = |Y_{lm}(\theta, \phi)|^2$

動作環境

・python 3.9.13
・IPython 8.4.0
・scipy 1.7.3
・matplotlib 3.5.2
・numpy 1.21.5
・Anaconda 4.14.0
・Spyder 5.9.2
・Windows10 64bit

参考

[1]. scipy_special.sph_harm(scipy公式ヘルプ)(参照2022-09-23)
[2]. 【Python】水素原子の解の描画：ラゲール陪多項式計算モジュール(参照2022-09-23)
[3]. Juliaで特殊関数を使う(参照2022-09-23)
[4]. Table of spherical harmonics(英語wikipedia)(参照2022-09-23)
[5]. 3D surface (checkerboard)(matplotlib公式ヘルプ)(参照2022-09-23)
[6]. Schiff. 量子力学（上）. 吉岡書店, 2004, p.88-93.
[7]. 猪木, 川合. 量子力学Ⅰ. 講談社サイエンティフィク, 2010, p.132-135.
[8]. J.J.Sakurai. 現代の量子力学（上）. 吉岡書店, 2006, p.347-348.
[9]. 球面調和関数(日本語wikipedia)(参照2022-09-23)
[10]. Spherical harmonics(英語wikipedia)(参照2022-09-23)
[11]. Associated Legendre polynomials(英語wikipedia)(参照2022-09-23)
[12]. Landau, Lifshitz. 量子力学1（非相対論的理論）, 東京図書, 1991, p.105-109.
[13]. Landau, Lifshitz. 量子力学2（非相対論的理論）, 東京図書, 1991, p.521-534.
[14]. 球面調和関数とその可視化(参照2022-09-23)
[15]. A.Szabo. 新しい量子化学（上）―電子構造の理論入門―. 東京大学出版会.
[16]. 朽津. 量子化学ノート. 分子化学アーカイブス(AC0016), 2013, p.129-142.(参照2022-09-23)
[17]. 日曜化学(3)：分子軌道法と可視化（Python/matplotlib）(参照2022-09-23)
[18]. 卜部. 化学Ⅰ・Ⅱの新研究. 三省堂, 2005, p.26.
[19]. 色空間(日本語wikipedia)(参照2022-09-23)
[20]. HSV色空間(日本語wikipedia)(参照2022-09-23)
[21]. 日曜化学：量子力学の基本と球面調和関数の可視化（Python/matplotlib）(参照2022-09-23)
[22]. 武内. 量子力学Ⅰ/球面調和関数（筑波大学講義ノート）.(参照2022-09-23)
[23]. Colorbar for matplotlib plot_surface using facecolors(stack overflow)(参照2022-09-23)
[24]. Juliaで可視化：水素原子(参照2022-09-23)
[25]. Table of spherical harmonics(英語wikipedia)(参照2022-09-23)