【Python】水素原子の可視化：ラゲール陪多項式計算モジュール

概要

scipy(python)のラゲール陪多項式（Associated Laguerre polynomial）を使用する際の注意点についての記事です。

水素原子におけるシュレディンガー方程式の解を描画したいと思った時、その解の中にラゲール陪多項式という特殊函数が出てきます。有難いことにscipyライブラリには、ラゲール陪多項式を計算するモジュールがあり、これを利用できます。（scipy.special.assoc_laguerreなど）

問題なのが、ラゲール陪多項式の定義が資料によって揺れており、恐らく殆ど全ての量子力学の教科書に載っている定義とscipyで実装されているものが異なるということです。
なので、量子力学の教科書を見ながらラゲール陪多項式の計算モジュールを使用すると高確率で間違えます。
ちなみに、多くの量子力学の教科書(参考[7-11])で、ラゲール陪多項式$L_n^k(x)$はラゲール多項式$L_n(x)$を用いて式$(1)$のように定義されます。ラゲール多項式$L_n(x)$は式$(2)$で定義されます。また、ラゲール陪多項式$L_n^k(x)$を多項式の形であからさまに書くと式$(3)$のようになります。

$$\begin{align} &L_n^k(x) = \frac{d^k}{dx^k} L_n \\ &L_n (x) = e^x \frac{d^n}{dx^n}(x^ne^{-x}) \\ &L_n^k(x) = \sum_{m=0}^{n-k} (-1)^{m+k} \frac{(n!)^2}{m!(m+k)!(n-m-k)!}x^m \end{align}$$

実際にscipyの実装との違いを確認した量子力学の教科書は、サクライ、シッフ、ランダウ、猪木・川合、（メシア）です(参考[7-11])。上記の教科書では、元となる定義式は違えど、式変形をしていけば式$(1)$～$(3)$に辿り着きます。（メシアだけは英語版wikipediaからの孫引き確認ですが、それ以外は直接原本を確認しました。）なので、上記の教科書を使用している方は要注意です。ただ、日本国内の大抵の教科書は上記のいずれかの教科書に準拠して作られていると思います。

よって、殆どの量子力学の教科書は式$(1)$～$(3)$のような定義をしていると疑われます。

また、この記事ではpythonのscipyライブライについてのみ解説しますが、Julia、Mathematicaなどでも同様の問題があるようです（Julia、mathematicaでの報告記事）。

ラゲール多項式とラゲール陪多項式が従う微分方程式は線形なので、その解を定数倍したものも解として認められます。よって、式$(1)$～$(3)$のような定義も別に間違いではないです。ただの流派の違いです。プログラムに実装するときに注意してくださいというだけの話です。

まずは結論（忙しい人用）

御託はいいから早くコードを修正したいという人は、式$(4)$のような変更をしてみて下さい。水素原子用のノーテーションを使っている人は式$(5)$のような変更になります。これで多分解決します。水素原子の動径波動関数$R_{nl}(r)$、動径確率密度分布$P_{nl}(r) = | r R_{nl}(r) |^2$が図1, 2のようになってしまい、なんかおかしいと思った人は下記のような修正をした方が良いです。図1, 2は間違った例なので注意してください。

$$\begin{align} L_m^k (x) &\rightarrow (-1)^k \cdot m! \cdot L^k_{m-k} (x) \\ L_{n+l}^{2l+1} (x) &\rightarrow (-1)^{2l+1} \cdot (n+l)! \cdot L^{2l+1}_{n-l-1} (x) \end{align}$$

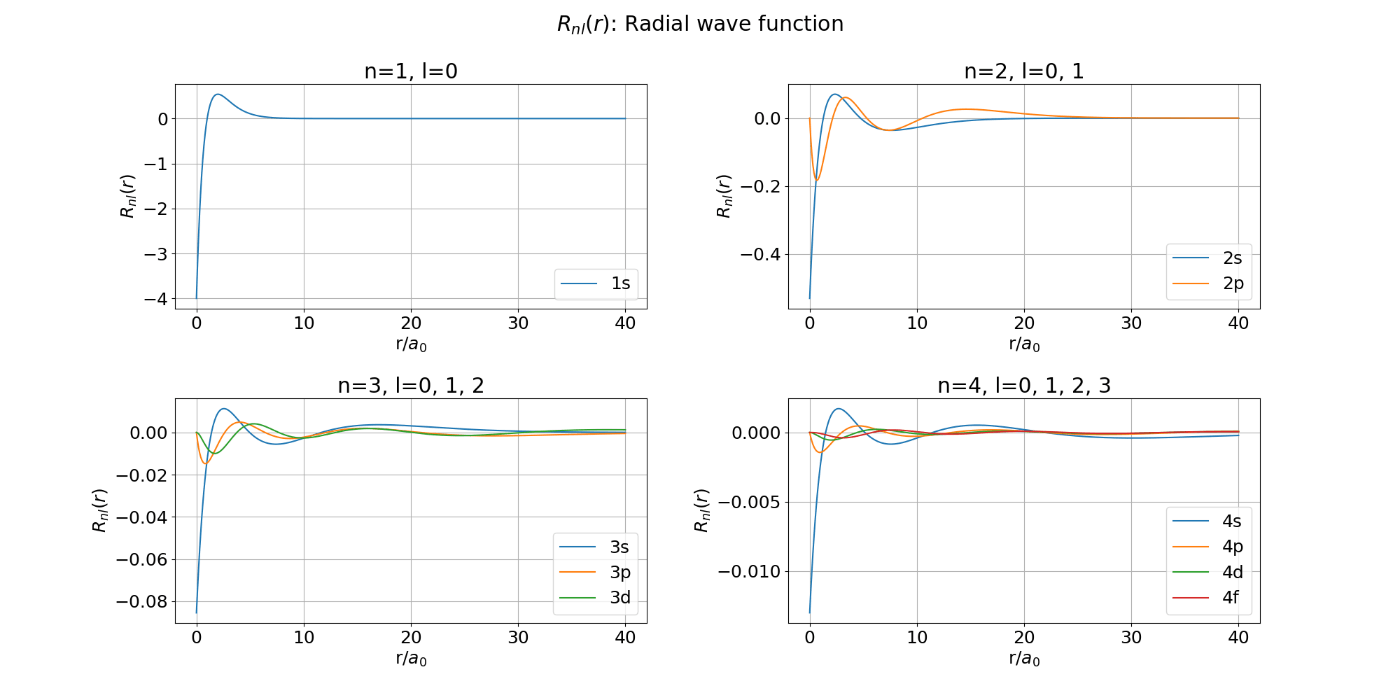
図1. 【間違った例】水素原子の動径波動関数：$R_{nl}(r)$

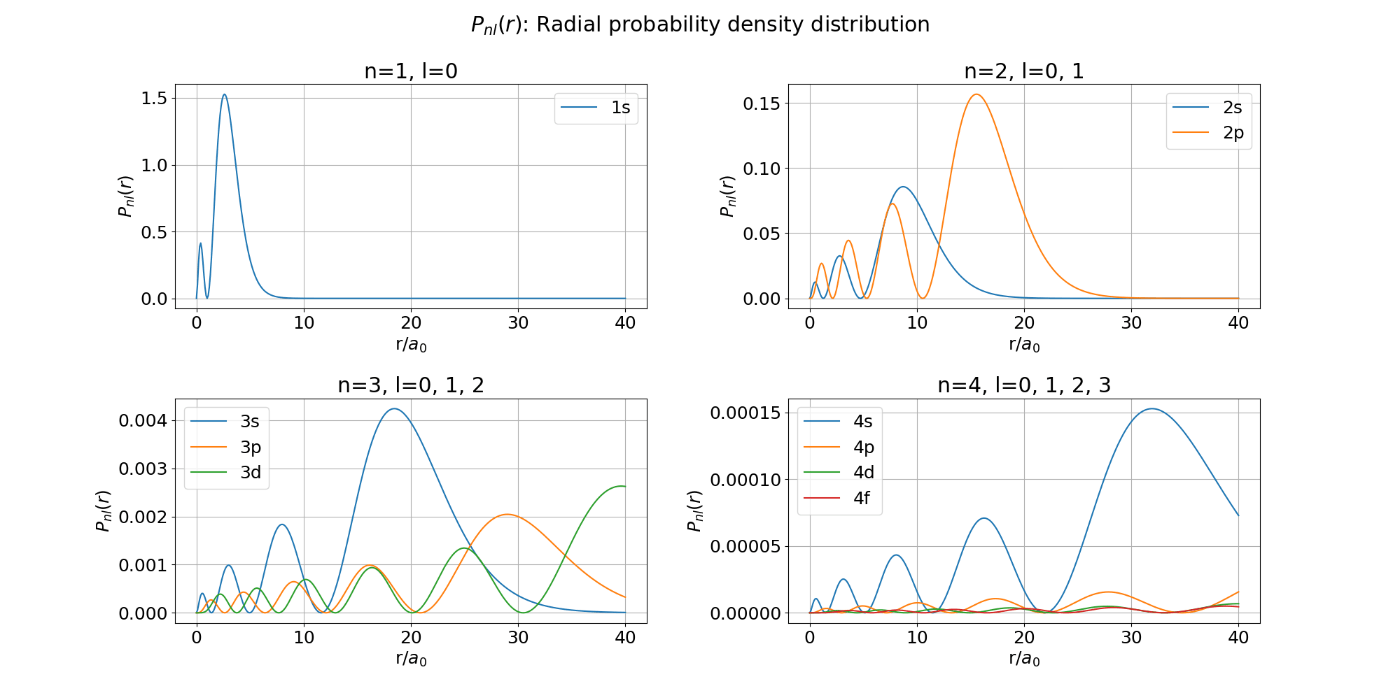
図2. 【間違った例】水素原子の動径確率密度分布：$P_{nl}(r) = | r R_{nl}(r) |^2$

下記はコードの変更例です。
適宜、アレンジしてください。

修正前

import scipy
'''
~~~ 中略 ~~~
'''
#コードのこの部分を
hoge = hoge2 * scipy.special.assoc_laguerre(x, n+l, 2*l+1)

修正後

import scipy
'''
~~~ 中略 ~~~
'''
#このように変更
coff = (-1)**(2*l+1) * scipy.special.factorial(n+l)
hoge = hoge2 * coff * scipy.special.assoc_laguerre(x, n-l-1, 2*l+1)

ラゲール陪多項式：scipyと量子力学の教科書の違い

scipyでは式$(6)$のようにラゲール陪多項式が定義されている(参考[1,2])。それに対し、量子力学の教科書では式$(7)$のように定義されている(参考[7-11])。
大きく違うのは$L_{\tilde{n}}^{(\alpha)}(x)$の係数が${\tilde{n}}$なのか$(n-k)$なのかという点。$\alpha$と$k$はそれぞれ、実数と整数という違いはあるが、プログラムに実装する上では特に困らない。式$(6)$において、$n$ではなく${\tilde{n}}$を使っているのは式$(6)$と式$(7)$で使われている${\tilde{n}}$と$n$の指し示す具体的な値が違いますよ、というのを明示的にしたいため。

$$\begin{align} &x \frac{d^2 L_{\tilde{n}}^{(\alpha)}}{dx^2} (x) + (\alpha+1-x)\frac{d L_{\tilde{n}}^{(\alpha)}(x)}{dx} + {\tilde{n}}L_{\tilde{n}}^{(\alpha)}(x) = 0 \\ &x \frac{d^2 L_n^{k}(x)}{dx^2} + (k+1-x)\frac{d L_n^{k}(x)}{dx} + (n-k)L_n^{k}(x) = 0 \\ \end{align}$$

式$(6)$と式$(7)$の違いにより、ラゲール陪多項式を露わに書き下したときに式$(8)$、$(9)$のような違いが出る。

$$\begin{align} L_{\tilde{n}}^{(\alpha)}(x) &= \sum_{m=0}^{\tilde{n}} (-1)^{m} \frac{(\tilde{n}+k)!}{m!(m+k)!(\tilde{n}-m)!} x^m \\ L_n^k(x) &= \sum_{m=0}^{n-k} (-1)^{m+k} \frac{(n!)^2}{m!(m+k)!(n-m-k)!}x^m \end{align}$$

式$(6)$と式$(7)$における係数の違いに注意し、式$(8)$で$\tilde{n} = n - k$という文字の置き換えをすると、式$(8)$は式$(10)$のようになる。

$$\begin{align} L_{n-k}^{(\alpha)}(x) &= \sum_{m=0}^{n-k} (-1)^{m} \frac{n!}{m!(m+k)!(n-m-k)!}x^m \end{align}$$

式$(9)$と式$(10)$の係数の違いを見比べると、式$(11)$が導かれる。これは冒頭で示した式$(4)$と同じものである。

$$\begin{align} L_n^k (x) = (-1)^k \cdot n! \cdot L^{(\alpha)}_{n-k} (x) \end{align}$$

ここで、式$(11)$の右辺における$(-1)^k$と$L^{(\alpha)}_{n-k}$の$n-k$はラゲール陪多項式の定義の違いにより生じたものである。一方、$\bm n!$はラゲール多項式の定義が違うことにより遺伝してきたものであることに注意したい。
ラゲール多項式の定義の違いも念のため書いておく。元となる微分方程式に違いは見られなかったが、解の形を露わに書き下すときに定数倍だけ違いが出てくる。元の微分方程式が線形なので、どちらの定義も正しく、どちらを採用するかは好みの問題である。式$(12)$がscipyの定義で、式$(13)$が物理の教科書の定義。式$(14)$は式$(12)$と$(13)$を結ぶ式。

$$\begin{align} L_n^{\rm scipy} (x) &= \sum_{m=0}^{n} (-1)^{m} \frac{n!}{(m!)^2(n-m)!}x^m \\ L_n^{\rm physics} (x) &= \sum_{m=0}^{n} (-1)^{m} \frac{(n!)^2}{(m!)^2(n-m)!}x^m \\ L_n^{\rm physics} (x) &= n! \cdot L_n^{\rm scipy} (x) \end{align}$$

検証：水素原子の動径波動関数と動径確率密度分布

上記まででscipyと物理の教科書との違いを述べたが、本当にそうなっているかを確認する。確認は水素原子の動径波動関数$R_{nl}(x)$と動径確率密度分布$P_{nl}(x) = |r R_{nl} (x)|^2$で行った。

スピンを考慮せず、電子と原子核の相互作用の影響をクーロンポテンシャルで置き換えると、定常状態における水素原子中の電子の波動関数$\Psi_{nlm} (r, \theta, \phi)$は式$(15)$のようなシュレディンガー方程式に従う。この微分方程式は変数分離型の微分方程式で、式$(16)$のように変数分離することができる。$R_{nl}(x)$は動径波動関数、$Y_l^m(\theta, \phi)$は球面調和関数である。

$$\begin{gather} \begin{split} \left[-\frac{\hbar^2}{2\mu} \left\{ \frac{1}{r} \frac{\partial^2}{\partial^2}r + \frac{1}{r^2 \rm sin\theta} \frac{\partial}{\partial \theta}\left( \rm sin\theta \frac{\partial}{\partial \theta} \right) + \frac{1}{r^2 \rm sin^2 \theta} \frac{\partial^2}{\partial \phi^2} \right\} -\frac{e^2}{r} \right]\Psi_{nlm} (r, \theta, \phi) \\= E_{nlm}\Psi_{nlm} (r, \theta, \phi) \end{split} \\ \Psi_{nlm} (r, \theta, \phi) = R_{nl} (r) Y_l^m(\theta, \phi) \end{gather}$$

動径波動関数はラゲール陪多項式を用いて式$(17)$のように書き下せる。式$(17)$中のラゲール陪多項式$L_{n+l}^{2l+1} (\zeta)$は物理の教科書の定義（例えば式$(9)$）に従う。詳細な導出方法は量子力学の教科書などを参考にされたい。日本語のwikipediaにも導出方法は記載されている。式$(17)$をscipyのラゲール陪多項式計算モジュールを使用して計算する場合は、式$(11)$に注意して、式$(19)$のような式を使用する必要がある。これは、この記事の結論となる式である。

$$\begin{gather} R_{nl} (r) = -\left\{ \left(\frac{2}{na_0} \right)^3 \frac{(n-l-1)!}{2n \left[ \left(n+l\right)!\right]^3} \right\}^{1/2} \cdot {\rm exp}\left(\frac{1}{2}\zeta\right) \cdot \zeta^l \cdot L_{n+l}^{2l+1} (\zeta) \\ a_0 = \frac{\hbar}{\mu e^2},\ \ \ \zeta = \frac{2}{n a_0}r,\ \ \ \mu = \frac{m_e m_p}{m_e + m_p} \\ \begin{split} R_{nl} (r) = -\left\{ \left(\frac{2}{na_0} \right)^3 \frac{(n-l-1)!}{2n \left[ \left(n+l\right)!\right]^3} \right\}^{1/2} \cdot {\rm exp}\left(\frac{1}{2}\zeta\right) \cdot \zeta^l \\ \cdot (-1)^{2l+1}\cdot (n+l)! \cdot L_{n-l-1}^{2l+1} (\zeta) \end{split} \end{gather}$$

scipyのラゲール陪多項式計算モジュールの動作確認は、水素原子の1s, 2p, 3d, 4s軌道に対して行った。計算モジュールを使用した場合と、式$(20)$～$(23)$のような関数をプログラム中にあからさまに記述した場合とで比較を行う。

$$\begin{align} &1s : R_{10} (r) = 2 \left( \frac{1}{a_0} \right)^{3/2} {\rm exp}\left(- \frac{r}{a_0} \right) \\ &2p : R_{21} (r) = \frac{1}{2 \sqrt{6}} \left( \frac{1}{a_0} \right)^{3/2} \frac{r}{a_0} {\rm exp}\left(- \frac{r}{2 a_0} \right) \\ &3d : R_{32} (r) = \frac{4}{81 \sqrt{30}} \left( \frac{1}{a_0} \right)^{3/2} \frac{r^2}{a_0^2} {\rm exp}\left(- \frac{r}{3 a_0} \right) \\ &4s : R_{40} (r) = \frac{1}{768} \left( \frac{1}{a_0} \right)^{3/2} \left( 192 - \frac{144 r}{a_0} + \frac{24 r^2}{a_0^2} - \frac{r^3}{a_0^3} \right) {\rm exp}\left(- \frac{r}{4 a_0} \right) \end{align}$$

図3, 4に動作確認の結果を示す。実線がscipyのラゲール陪多項式計算モジュールを使用した場合の結果で、ドットで示しているのがプログラム中に関数をあからさまに記述した場合の結果である。図3, 4ともに実線とドットは重なっているので、計算モジュールを意図した通りに使用できていることが分かった。

図3. ラゲール陪多項式計算モジュールの動作確認：動径波動関数$R_{nl}(r)$

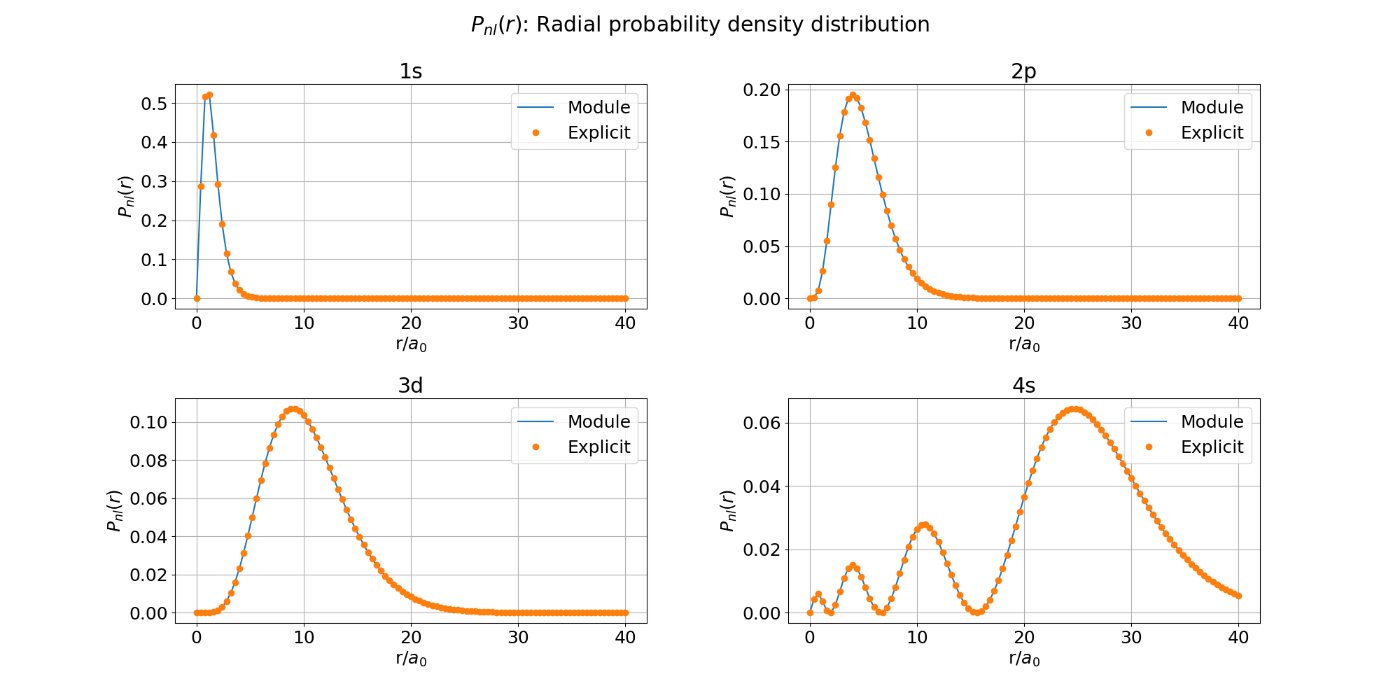
図4. ラゲール陪多項式計算モジュールの動作確認：動径確率密度分布$P_{nl}(r) = |r R_{nl} (r)|^2$

使用したプログラムは下記。

グラフ描画のところが少し冗長ですが、可読性を重視してこのような形にしています。for文等で短く記述しても良いと思います。

検証用プログラム

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import factorial
from scipy.special import assoc_laguerre

#動径波動関数
def R_nl(r, n, l):
    
    a0 = 1.0
    zeta = 2.0/n/a0 * r
    
    #修正係数
    n_d = n-l-1
    L_coff = (-1)**(2*l+1) * factorial(n+l)
    
    f_coff = - ((2.0/n/a0)**3 * factorial(n-l-1)/2.0/n/factorial(n+l)**3)**(1.0/2.0)
    f = f_coff * np.exp(-zeta/2.0) * zeta**l * L_coff * assoc_laguerre(zeta, n_d, 2*l+1)
    
    return f

Nr = 101
rmin = 0.0
rmax = 40.0

r = np.linspace(rmin, rmax, Nr)

#動径波動関数の計算
#ラゲール陪多項式の計算モジュール使用
R_nl_1s = R_nl(r, 1, 0)
R_nl_2p = R_nl(r, 2, 1)
R_nl_3d = R_nl(r, 3, 2)
R_nl_4s = R_nl(r, 4, 0)
#関数ベタ打ち
a00 = 1.0
R_nl_1s_exp = 2 * (1/a00)**(3/2) * np.exp(-r/a00)
R_nl_2p_exp = (1/2/a00)**(3/2) * r/np.sqrt(3)/a00 * np.exp(-r/2/a00)
R_nl_3d_exp = 4/81/np.sqrt(30) * (1/a00) ** (3/2) * r**2/a00**2 * np.exp(-r/3/a00)
R_nl_4s_exp = 1/768 * (1/a00)**(3/2) * (192 - 144*r/a00 + 24*r**2/a00**2 - r**3/a00**3)*np.exp(-r/4/a00)

#動径確率密度分布の計算
#ラゲール陪多項式の計算モジュール使用
P_nl_1s = r**2 * R_nl_1s**2
P_nl_2p = r**2 * R_nl_2p**2
P_nl_3d = r**2 * R_nl_3d**2
P_nl_4s = r**2 * R_nl_4s**2
#関数ベタ打ち
P_nl_1s_exp = r**2 * R_nl_1s_exp**2
P_nl_2p_exp = r**2 * R_nl_2p_exp**2
P_nl_3d_exp = r**2 * R_nl_3d_exp**2
P_nl_4s_exp = r**2 * R_nl_4s_exp**2


#グラフフォントサイズ
plt.rcParams["font.size"] = 18

#動径波動関数の描画
fig1, ax1 = plt.subplots(2,2, figsize=(20,10))
fig1.subplots_adjust(hspace=0.4, wspace=0.3)
fig1.suptitle('$R_{nl}(r)$: Radial wave function')

ax1[0][0].plot(r, R_nl_1s, label='Module')
ax1[0][1].plot(r, R_nl_2p, label='Module')
ax1[1][0].plot(r, R_nl_3d, label='Module')
ax1[1][1].plot(r, R_nl_4s, label='Module')

ax1[0][0].plot(r, R_nl_1s_exp, label='Explicit', linestyle='None', marker='o')
ax1[0][1].plot(r, R_nl_2p_exp, label='Explicit', linestyle='None', marker='o')
ax1[1][0].plot(r, R_nl_3d_exp, label='Explicit', linestyle='None', marker='o')
ax1[1][1].plot(r, R_nl_4s_exp, label='Explicit', linestyle='None', marker='o')

ax1[0][0].set_title('1s')
ax1[0][1].set_title('2p')
ax1[1][0].set_title('3d')
ax1[1][1].set_title('4s')

for i in range(2):
    for j in range(2):
        ax1[i][j].grid()
        ax1[i][j].legend()
        ax1[i][j].set_xlabel('r/$a_0$')
        ax1[i][j].set_ylabel('$R_{nl}(r)$')

#動径確率密度分布の描画
fig2, ax2 = plt.subplots(2,2, figsize=(20,10))
fig2.subplots_adjust(hspace=0.4, wspace=0.3)
fig2.suptitle('$P_{nl}(r)$: Radial probability density distribution')

ax2[0][0].plot(r, P_nl_1s, label='Module')
ax2[0][1].plot(r, P_nl_2p, label='Module')
ax2[1][0].plot(r, P_nl_3d, label='Module')
ax2[1][1].plot(r, P_nl_4s, label='Module')

ax2[0][0].plot(r, P_nl_1s_exp, label='Explicit', linestyle='None', marker='o')
ax2[0][1].plot(r, P_nl_2p_exp, label='Explicit', linestyle='None', marker='o')
ax2[1][0].plot(r, P_nl_3d_exp, label='Explicit', linestyle='None', marker='o')
ax2[1][1].plot(r, P_nl_4s_exp, label='Explicit', linestyle='None', marker='o')

ax2[0][0].set_title('1s')
ax2[0][1].set_title('2p')
ax2[1][0].set_title('3d')
ax2[1][1].set_title('4s')

for i in range(2):
    for j in range(2):
        ax2[i][j].grid()
        ax2[i][j].legend()
        ax2[i][j].set_xlabel('r/$a_0$')
        ax2[i][j].set_ylabel('$P_{nl}(r)$')

水素原子の1s～4f軌道

本来の目的は水素原子の動径波動関数$R_{nl}(r)$と動径確率密度分布$P_{nl} (r) = |r R_{nl}(r)|^2$を描画することなので、1s～4f軌道について描画した結果を図5, 6に示す。問題なく描画できていることが分かる。

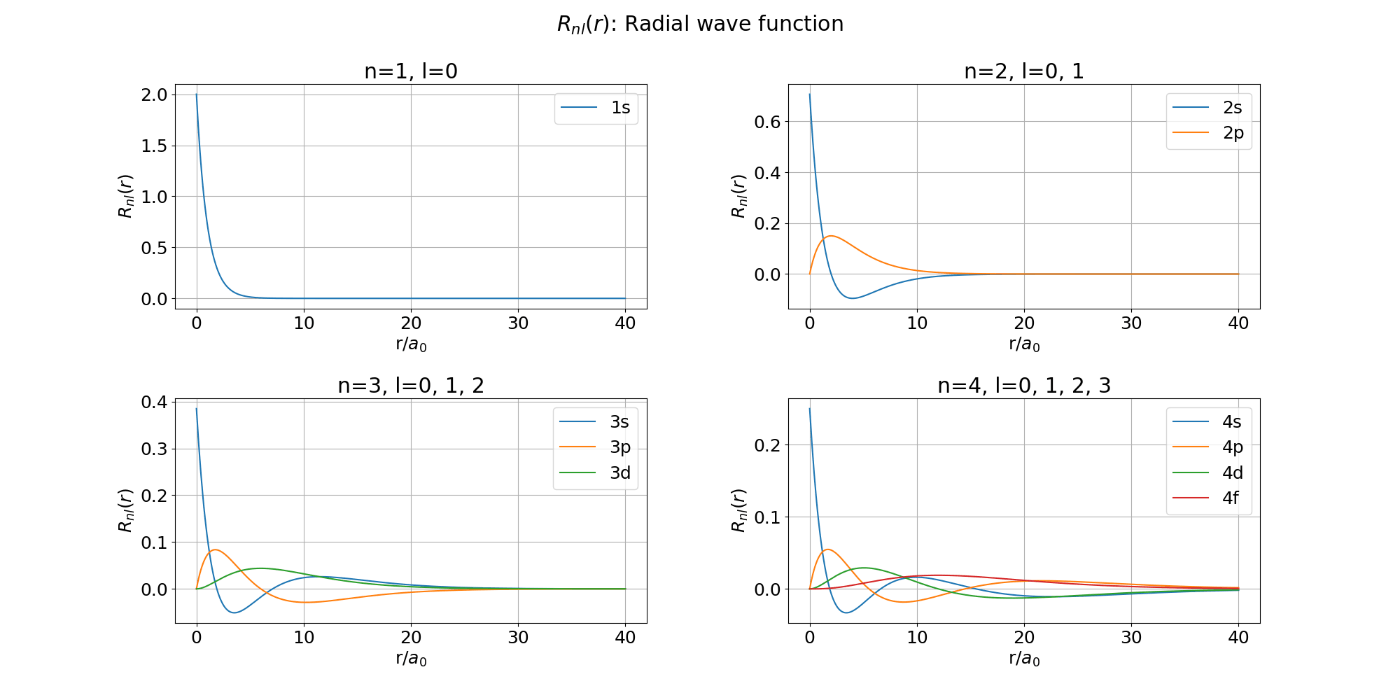
図5. 水素原子の動径波動関数：$R_{nl}(r)$ （1s～4d軌道）

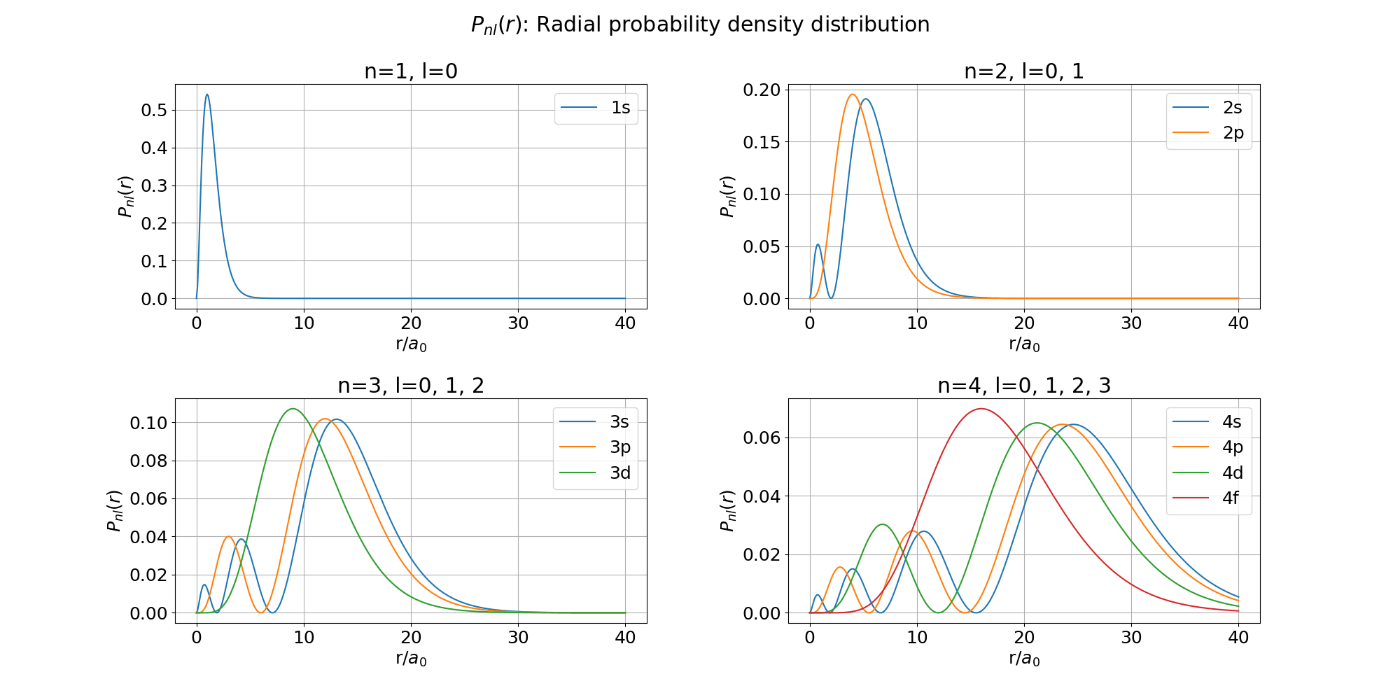
図6. 水素原子の動径確率密度分布：$P_{nl} (r) = |r R_{nl}(r)|^2$ （1s～4d軌道）

使用したプログラムは下記。

グラフ描画のところが少し冗長ですが、可読性を重視してこのような形にしています。for文等で短く記述しても良いと思います。先述の検証用プログムとほぼ同じものです。

使用プログラム：動径波動関数と動径確率密度分布

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import factorial
from scipy.special import assoc_laguerre

#動径波動関数
def R_nl(r, n, l):
    
    a0 = 1.0
    zeta = 2.0/n/a0 * r
    
    #修正係数
    n_d = n-l-1
    L_coff = (-1)**(2*l+1) * factorial(n+l)
    
    f_coff = - ((2.0/n/a0)**3 * factorial(n-l-1)/2.0/n/factorial(n+l)**3)**(1.0/2.0)
    f = f_coff * np.exp(-zeta/2.0) * zeta**l * L_coff * assoc_laguerre(zeta, n_d, 2*l+1)
    
    return f

Nr = 401
rmin = 0.0
rmax = 40.0

r = np.linspace(rmin, rmax, Nr)

#動径波動関数の計算
R_nl_1s = R_nl(r, 1, 0)
R_nl_2s = R_nl(r, 2, 0)
R_nl_2p = R_nl(r, 2, 1)
R_nl_3s = R_nl(r, 3, 0)
R_nl_3p = R_nl(r, 3, 1)
R_nl_3d = R_nl(r, 3, 2)
R_nl_4s = R_nl(r, 4, 0)
R_nl_4p = R_nl(r, 4, 1)
R_nl_4d = R_nl(r, 4, 2)
R_nl_4f = R_nl(r, 4, 3)

#動径確率密度分布の計算
P_nl_1s = r**2 * R_nl_1s**2
P_nl_2s = r**2 * R_nl_2s**2
P_nl_2p = r**2 * R_nl_2p**2
P_nl_3s = r**2 * R_nl_3s**2
P_nl_3p = r**2 * R_nl_3p**2
P_nl_3d = r**2 * R_nl_3d**2
P_nl_4s = r**2 * R_nl_4s**2
P_nl_4p = r**2 * R_nl_4p**2
P_nl_4d = r**2 * R_nl_4d**2
P_nl_4f = r**2 * R_nl_4f**2


#グラフフォントサイズ
plt.rcParams["font.size"] = 18

#動径波動関数の描画
fig1, ax1 = plt.subplots(2,2, figsize=(20,10))
fig1.subplots_adjust(hspace=0.4, wspace=0.3)
fig1.suptitle('$R_{nl}(r)$: Radial wave function')

ax1[0][0].plot(r, R_nl_1s, label='1s')
ax1[0][1].plot(r, R_nl_2s, label='2s')
ax1[0][1].plot(r, R_nl_2p, label='2p')
ax1[1][0].plot(r, R_nl_3s, label='3s')
ax1[1][0].plot(r, R_nl_3p, label='3p')
ax1[1][0].plot(r, R_nl_3d, label='3d')
ax1[1][1].plot(r, R_nl_4s, label='4s')
ax1[1][1].plot(r, R_nl_4p, label='4p')
ax1[1][1].plot(r, R_nl_4d, label='4d')
ax1[1][1].plot(r, R_nl_4f, label='4f')

ax1[0][0].set_title('n=1, l=0')
ax1[0][1].set_title('n=2, l=0, 1')
ax1[1][0].set_title('n=3, l=0, 1, 2')
ax1[1][1].set_title('n=4, l=0, 1, 2, 3')

for i in range(2):
    for j in range(2):
        ax1[i][j].grid()
        ax1[i][j].legend()
        ax1[i][j].set_xlabel('r/$a_0$')
        ax1[i][j].set_ylabel('$R_{nl}(r)$')


#動径確率密度分布の描画
fig2, ax2 = plt.subplots(2,2, figsize=(20,10))
fig2.subplots_adjust(hspace=0.4, wspace=0.3)
fig2.suptitle('$P_{nl}(r)$: Radial probability density distribution')

ax2[0][0].plot(r, P_nl_1s, label='1s')
ax2[0][1].plot(r, P_nl_2s, label='2s')
ax2[0][1].plot(r, P_nl_2p, label='2p')
ax2[1][0].plot(r, P_nl_3s, label='3s')
ax2[1][0].plot(r, P_nl_3p, label='3p')
ax2[1][0].plot(r, P_nl_3d, label='3d')
ax2[1][1].plot(r, P_nl_4s, label='4s')
ax2[1][1].plot(r, P_nl_4p, label='4p')
ax2[1][1].plot(r, P_nl_4d, label='4d')
ax2[1][1].plot(r, P_nl_4f, label='4f')

ax2[0][0].set_title('n=1, l=0')
ax2[0][1].set_title('n=2, l=0, 1')
ax2[1][0].set_title('n=3, l=0, 1, 2')
ax2[1][1].set_title('n=4, l=0, 1, 2, 3')

for i in range(2):
    for j in range(2):
        ax2[i][j].grid()
        ax2[i][j].legend()
        ax2[i][j].set_xlabel('r/$a_0$')
        ax2[i][j].set_ylabel('$P_{nl}(r)$')
        
#画像の保存
fig1.savefig('動径波動関数')
fig2.savefig('動径確率密度分布')

動作環境

・python 3.9.13
・scipy 1.7.3
・Spyder 5.9.2
・Windows10 64bit

参考

[1]. scipy.special.assoc_laguerre(scipy公式ヘルプ)(参照2022-09-11)
[2]. scipy.special.genlaguerre(scipy公式ヘルプ)(参照2022-09-11)
[3]. Juliaで可視化：水素原子（参照2022-09-11）
[4]. ラゲールの陪多項式とassociated Laguerre polynomialsの指しているものが違った件（参照2022-09-11）
[5]. ラゲール多項式(英語版wikipedia)(参照2022-09-11)
[6]. ラゲールの陪多項式(日本語版wikipedia)(参照2022-09-11)
[7]. J.J.Sakurai. 現代の量子力学（上）. 吉岡書店, 2006, p.351-353.
[8]. Schiff. 量子力学（上）. 吉岡書店, 2004, p.106-108.
[9]. Landau, Lifshitz. 量子力学1（非相対論的理論）, 東京図書, 1991, p.138-142.
[10]. 猪木, 川合. 量子力学Ⅰ. 講談社サイエンティフィク, 2010, p.148-152.
[11]. Messiah, Albert. Quantum Mechanics. 2014.