Zenn
💯

Antique.jlの紹介

2023/12/11に公開
Julia
math
量子力学
物理
化学
idea

Julia Advent Calendar 2023 11日目です🎄

はじめに

量子力学に関わる学生・教員・研究者にとって便利なパッケージ「Antique.jl」を開発いたしましたのでご紹介いたします. 学生にとってはプレゼン資料, 教員にとっては量子力学の教材, 研究者にとっては計算手法のベンチマークなどに活用できます. それぞれの活用例を後述しておりますのでご一読ください.

Antique.jl


https://ohno.github.io/Antique.jl/

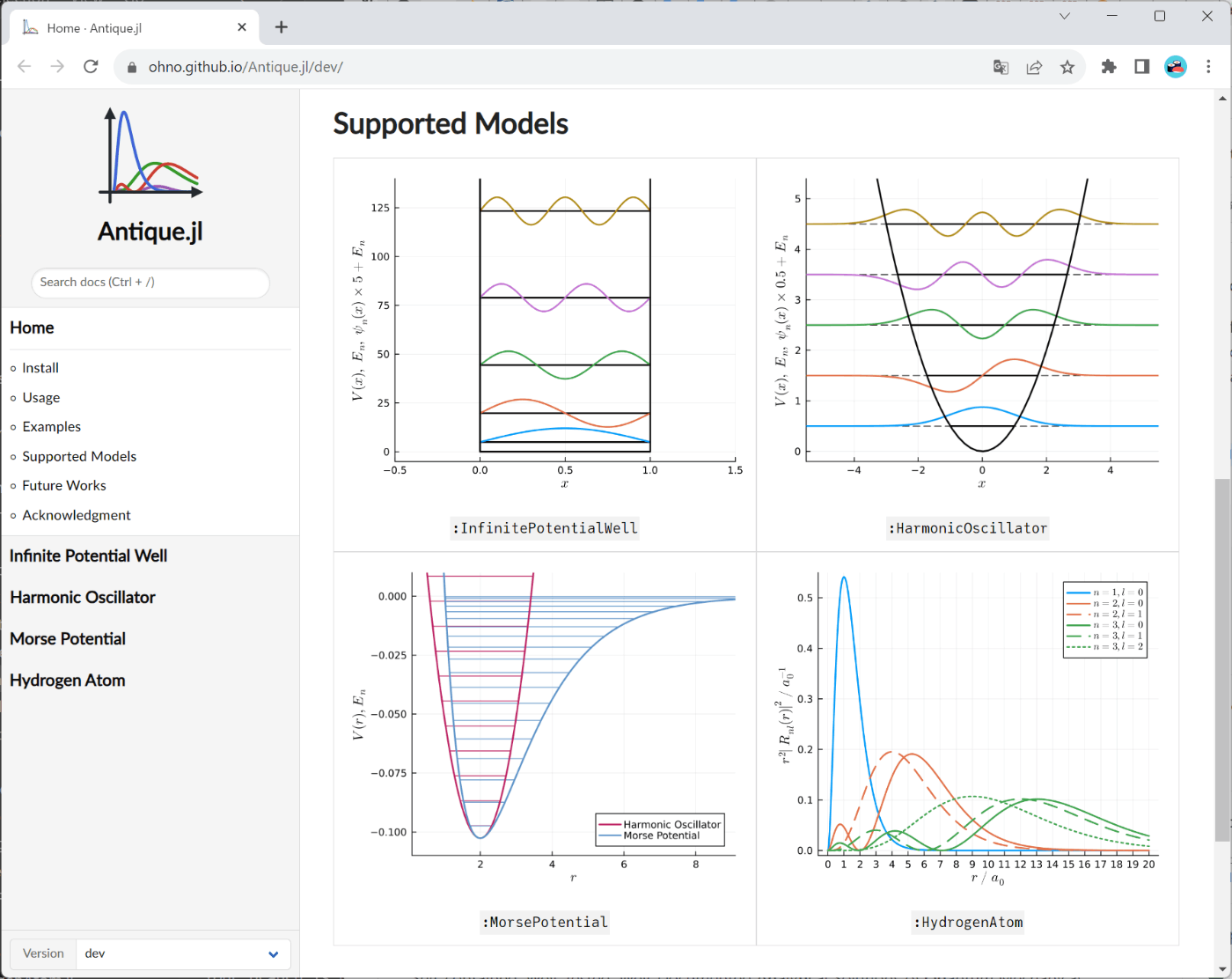
このパッケージは現在, 無限に深い井戸型ポテンシャル, 調和振動子, モースポテンシャル, 水素原子 の4つのモデルをサポートしており, これらのモデルにおけるSchrödinger方程式の解析解（固有値, 固有関数）やポテンシャル等をまとめたモジュールを提供します. いずれのモデルに対しても数値積分（QuadGK.jl）または数式処理システム（Symbolics.jl）を用いたテストを行っています. 今後はこちらのリストにあるモデルを順次追加していく予定です. Issueにリクエストを頂ければ優先的に対応します.

なぜ必要なのか？

一言でいえば「解析解の実装がとにかく面倒くさいから」です. 新しい手法を作ろうとしているのにベンチマークの実装やテストに手間を取られていては本末転倒ですから, パッケージにまとめてしまおうという魂胆です.

リリースまでの道のり

時は昨年（2022年）の1月に遡ります. Juliaで可視化シリーズと題して3つの記事を公開しました.

https://zenn.dev/ohno/articles/870b0c2a0af590

https://zenn.dev/ohno/articles/f849d98a7f58a9

https://zenn.dev/ohno/articles/e1103bc0d58ceb

これらの記事を書いた目的は前述の通り計算手法のベンチマークとすることでしたが, 学会発表や修論発表で量子力学的な概念（零点振動, Born-Oppenheimer近似, 振動励起状態など）の説明する図としても活用しました. Antique.jlでは, これらの記事で定義したを解析解（固有値・固有関数）やポテンシャルなどを, それぞれ1つのモジュールにまとめたもの（の改良版）を提供しています.

記事をお読み頂くと, とりわけ水素原子の固有関数に含まれるLaguerre陪多項式とLegendre陪多項式の扱いで苦労していることがわかると思います. これらの多項式はロドリゲスの公式を用いて定義されることがほとんどですが, ロドリゲスの公式には微分演算が含まれており実装が困難なため, 実装では閉形式または漸化式が利用されます. しかし, ほとんどの量子力学の教科書には閉形式は併記されていないため, 実装は困難です. 直交多項式などの公式集やパッケージは既にありますが, どのような定義（ロドリゲスの公式）に基づいた実装なのかが不明確であったり, そもそも教科書とは定義が違う（微分方程式の解なのでいくらかの差異が許される）ため閉形式をそのまま利用できないなど, 確認作業（テスト）に膨大な時間がかかりました.

この問題を解決するため, 去年（2022年）のアドベントカレンダーではSymbolics.jlを用いてロドリゲスの公式の展開結果と閉形式が一致するか自動的にテストする方法について記事を書きました. この記事におけるテスト技法を実際に活用しています.

https://zenn.dev/ohno/articles/0aaace3224c4fa

また, Juliaで可視化シリーズでは数値積分を用いて固有関数の直交性, 固有値, ビリアル定理などを検証していました. Antique.jlでは数値積分と数式処理を併用したテストを採用しています. 興味のある方はテスト技法の紹介についてご覧ください. 以降は2つの活用例についてご紹介いたします.

インストール

REPLやJupyter Notebook上などで下記を実行するだけです. 使用方法は活用例を通して解説します.

using Pkg; Pkg.add("Antique")

活用例：量子力学の教材

元々の用途は手法開発におけるベンチマークを提供することですが量子力学の教材としても非常に便利です. まず, 水素原子のモジュールを取得しましょう.

using Antique
H = HydrogenAtom(Z=1, Eₕ=1.0, a₀=1.0, mₑ=1.0, ℏ=1.0)

ではライマン系列の波長を計算してみましょう.

# ライマン系列 n -> 1
wavelength(ΔE) = 1 / (ΔE * 2.1947463136320e-2) # nm, https://physics.nist.gov/cgi-bin/cuu/CCValue?hrminv
for i in 2:7
    println("$i -> 1\t", wavelength( E(H,n=i) - E(H,n=1) ), " nm")
end

# output
2 -> 1	121.50227341098497 nm
3 -> 1	102.51754319051858 nm
4 -> 1	97.20181872878798 nm
5 -> 1	94.92365110233202 nm
6 -> 1	93.73032520275984 nm
7 -> 1	93.02517808028537 nm

いずれの波長もWikipediaの値と一致しています. 次に動径分布関数をプロットしてみましょう.

using Plots
plot(xlabel="\$r~/~a_0\$", ylabel="\$r^2|R_{nl}(r)|^2~/~a_0^{-1}\$", ylims=(-0.01,0.55), xticks=0:1:20, size=(480,400), dpi=300)
for n in 1:3
  for l in 0:n-1
    plot!(0:0.01:20, r->r^2*Antique.R(H,r,n=n,l=l)^2, lc=n, lw=2, ls=[:solid,:dash,:dot,:dashdot,:dashdotdot][l+1], label="\$n = $n, l=$l\$")
  end
end
plot!()

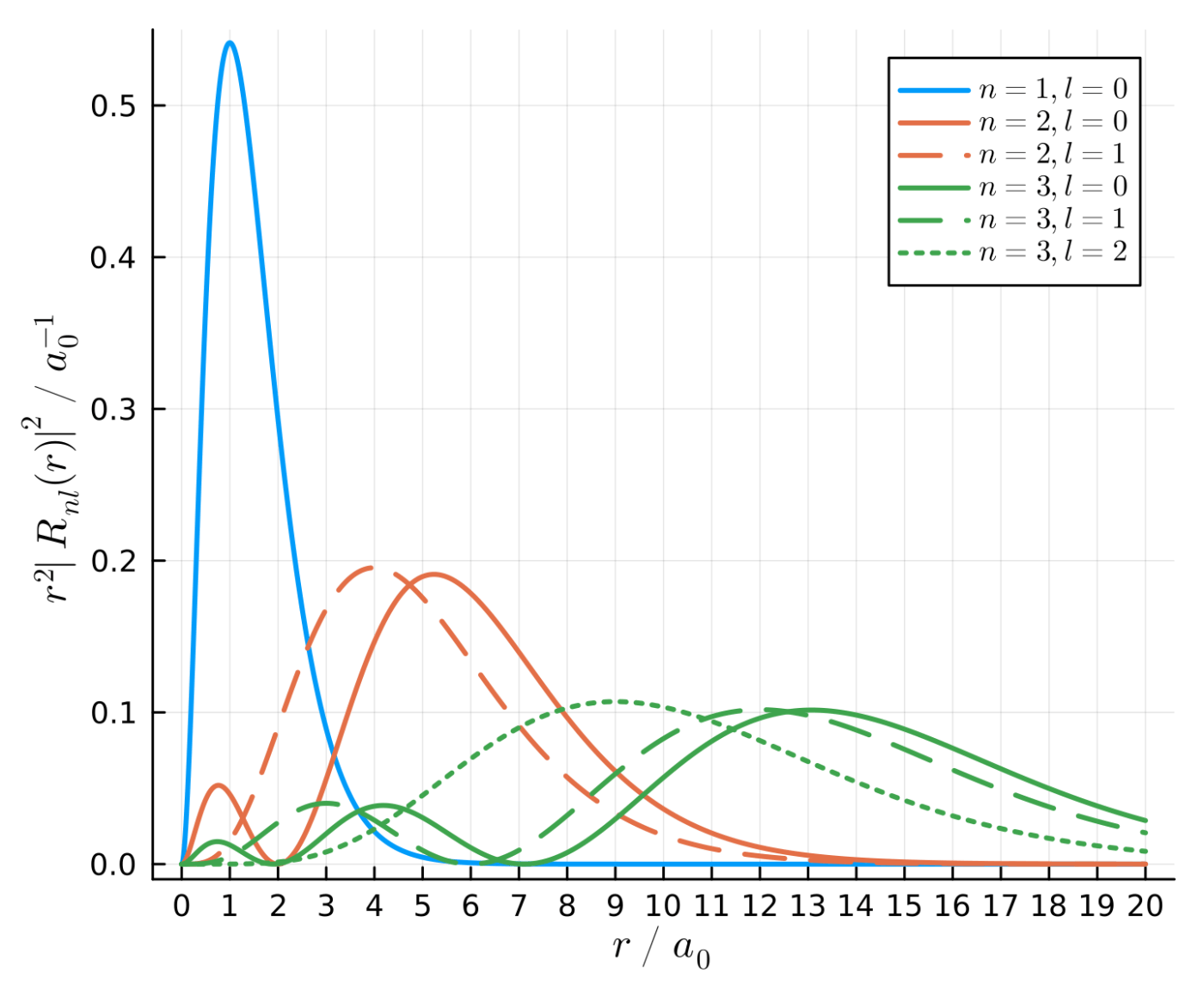
こちらのグラフとよく一致しています. なお, 2\mathrm{p_x}や2\mathrm{p_y}のような実数化された軌道ではないので注意してください. 上記の固有関数の線形結合を取って虚部を消す必要があります. では最後に超微細分離の波長（21cm線）を計算してみましょう.

# constants: https://doi.org/10.1103/RevModPhys.93.025010
e  = 1.602176634e-19    # C      https://physics.nist.gov/cgi-bin/cuu/Value?e
h  = 6.62607015e-34     # J Hz-1 https://physics.nist.gov/cgi-bin/cuu/Value?h
c  = 299792458          # m s-1  https://physics.nist.gov/cgi-bin/cuu/Value?c
a0 = 5.29177210903e-11  # m      https://physics.nist.gov/cgi-bin/cuu/Value?bohrrada0
µ0 = 1.25663706212e-6   # N A-2  https://physics.nist.gov/cgi-bin/cuu/Value?mu0
µB = 9.2740100783e-24   # J T-1  https://physics.nist.gov/cgi-bin/cuu/Value?mub
µN = 5.0507837461e-27   # J T-1  https://physics.nist.gov/cgi-bin/cuu/Value?mun
ge = 2.00231930436256   #        https://physics.nist.gov/cgi-bin/cuu/Value?gem
gp = 5.5856946893       #        https://physics.nist.gov/cgi-bin/cuu/Value?gp

# calculation: https://doi.org/10.1119/1.12733
δ = abs(ψ(H,0,0,0))^2
ΔE = 2 / 3 * µ0 * µN * µB * gp * ge * δ * a0^(-3)
println("1/π    = ", 1/π)
println("<δ(r)> = ", δ, " a₀⁻³")
println("<δ(r)> = ", δ * a0^(-3), " m⁻³")
println("ΔE = ", ΔE, " J")
println("ν = ΔE/h = ", ΔE / h * 1e-6, " MHz")
println("λ = hc/ΔE = ", h*c/ΔE*100, " cm")

# output
1/π    = 0.3183098861837907
<δ(r)> = 0.3183098861837908 a₀⁻³
<δ(r)> = 2.1480615849063944e30 m⁻³
ΔE = 9.427622831641132e-25 J
ν = ΔE/h = 1422.8075794882932 MHz
λ = hc/ΔE = 21.070485027063118 cm

ここではGriffiths(1982)を参考に, 基底状態の波動関数（の絶対値の2乗）のr=0における値を用いて摂動的に超微細分離のエネルギー差, 振動数, 波長を計算しました. 21cm線の名で知られている通り, 波長が約21cmであることが計算できました. 結果に表示されている1/πは\langle \delta^3(\pmb{r}) \rangle_\mathrm{1S} = |\psi_\mathrm{1S}(\pmb{0})|^2 = \frac{1}{\pi} a_0^{-3}の単位を除いた値に対応しています. 水素原子の原点の確率密度（陽子と電子が同じ位置に存在する確率）として1/\piという綺麗な数字が現れるところが好きです.

これらの例の他にも固有関数の直交性, ビリアル定理や各種の物理量の期待値の計算がテストとして実装・運用されています. いずれも演習や課題の良い題材になると思われます.

活用例：計算手法のベンチマーク

QuantumOptics.jlで調和振動子の固有値および固有関数が計算できます. 計算した固有値がAntique.jlの値と一致するかテストしてみましょう.

# Parameters
k = 1.0
m = 1.0
ℏ = 1.0

# https://ohno.github.io/Antique.jl/dev/HarmonicOscillator/#Usage-and-Examples
# using Pkg; Pkg.add("Antique")
using Antique
HO = HarmonicOscillator(k=k, m=m, ℏ=ℏ)

# https://qojulia.org/
# using Pkg; Pkg.add("QuantumOptics")
using QuantumOptics
basis = PositionBasis(-5, 5, 100)
x = position(basis)
p = momentum(basis)
H = p^2*ℏ^2/2/m + k/2*DenseOperator(x^2)
energies, states = eigenstates((H+dagger(H))/2, 10)

# Antique.jl vs QuantumOptics.jl
using Printf
println(" n\tAntique.jl(exact)  \tQuantumOptics.jl")
for i in keys(energies)
    @printf("%2d\t%.15f\t%.15f\n", i-1, E(HO,n=i-1), energies[i])
end

 n	Antique.jl(exact)  	QuantumOptics.jl
 0	0.500000000000000	0.499999999920220
 1	1.500000000000000	1.500000003671307
 2	2.500000000000000	2.499999911435342
 3	3.500000000000000	3.500001221372221
 4	4.500000000000000	4.499986371258386
 5	5.500000000000000	5.500098711913332
 6	6.500000000000000	6.499320233969457
 7	7.500000000000000	7.502927850989741
 8	8.500000000000000	8.485825750231648
 9	9.500000000000000	9.536571503980930

QuantumOptics.jlは調和振動子をかなり精度よく計算できていることがわかります. ここでは空間基底の範囲を-5から5までとしていますが, これを狭くするとかなり記述が悪くなります. また, 基底の範囲だけでなく, 高い励起状態では節が多くなりますので, 十分なグリッドの細かさがないと記述が悪くなります. もちろんパラメータによっても記述の良さは変化します. 試してみてください.

一応, 確率密度関数もプロットしておきましょう. どうやらstates[n].dataは\sum |\psi(x)|^2 \Delta x=1ではなく\sum |\psi(x)|^2=1で規格化されているようなので\Delta xで割ってやる必要があります.

using Plots
default(lw=2)
X = samplepoints(basis)
Δx = (maximum(X) - minimum(X)) / length(X)
for i in 0:9
    plot(xlabel="x", ylabel="ψ(x)", title="v = $i")
    plot!(-5:0.01:5, x -> abs(ψ(HO,x,n=i))^2, label="Antique.jl(exact)")
    scatter!(X, abs2.(states[i+1].data) / Δx, label="QuantumOptics.jl", ms=3, msw=0)
    plot!() |> display
end

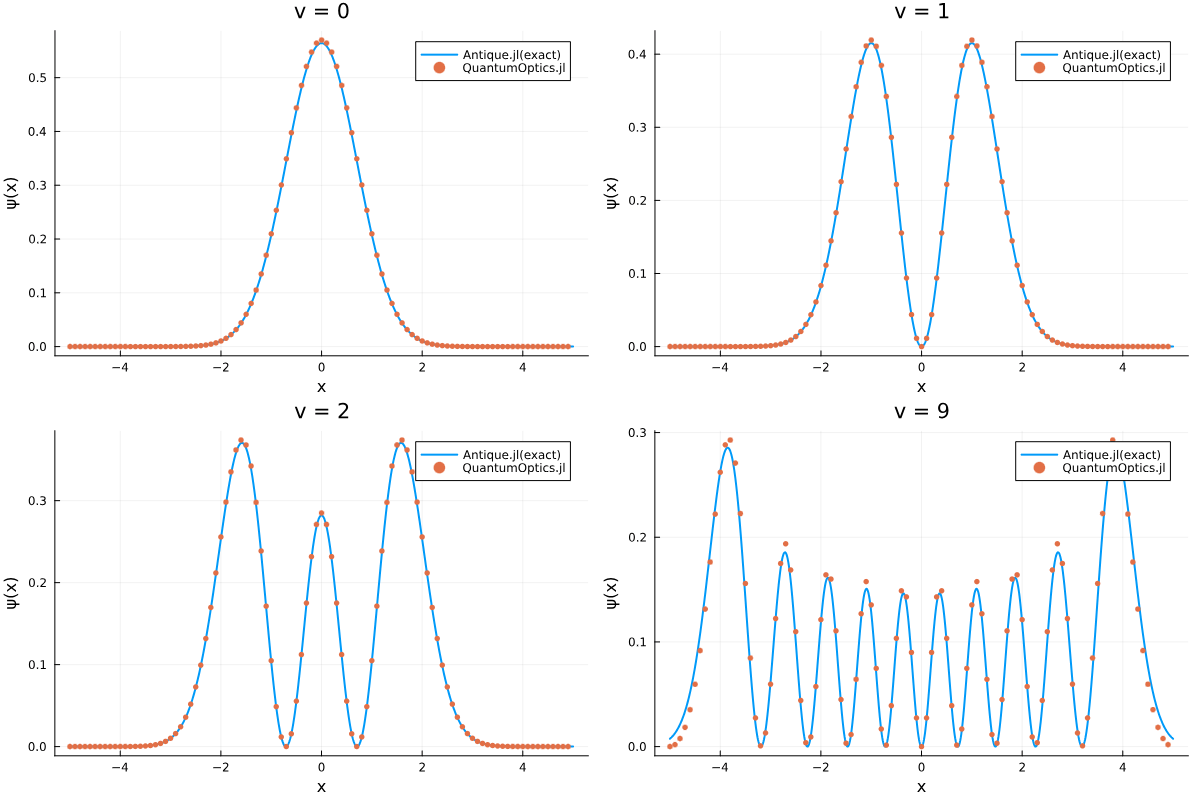
非常に良く一致しています. 高い励起状態で記述が悪くなる様子も確認できました.

おわりに

これから新しい手法を開発する方はぜひベンチマークとしてご利用ください. 新しいモデルのリクエスト等はこちらまでお願いいたします. スターお待ちしております🌟

https://github.com/ohno/Antique.jl

https://ohno.github.io/Antique.jl/dev/

開発者向け

ドキュメントの紹介

ドキュメントの紹介

各モデルのドキュメントにはそれぞれ

  • モデルのself-containedな説明
  • 使用方法と具体例
  • 数式処理および数値積分を用いたテスト

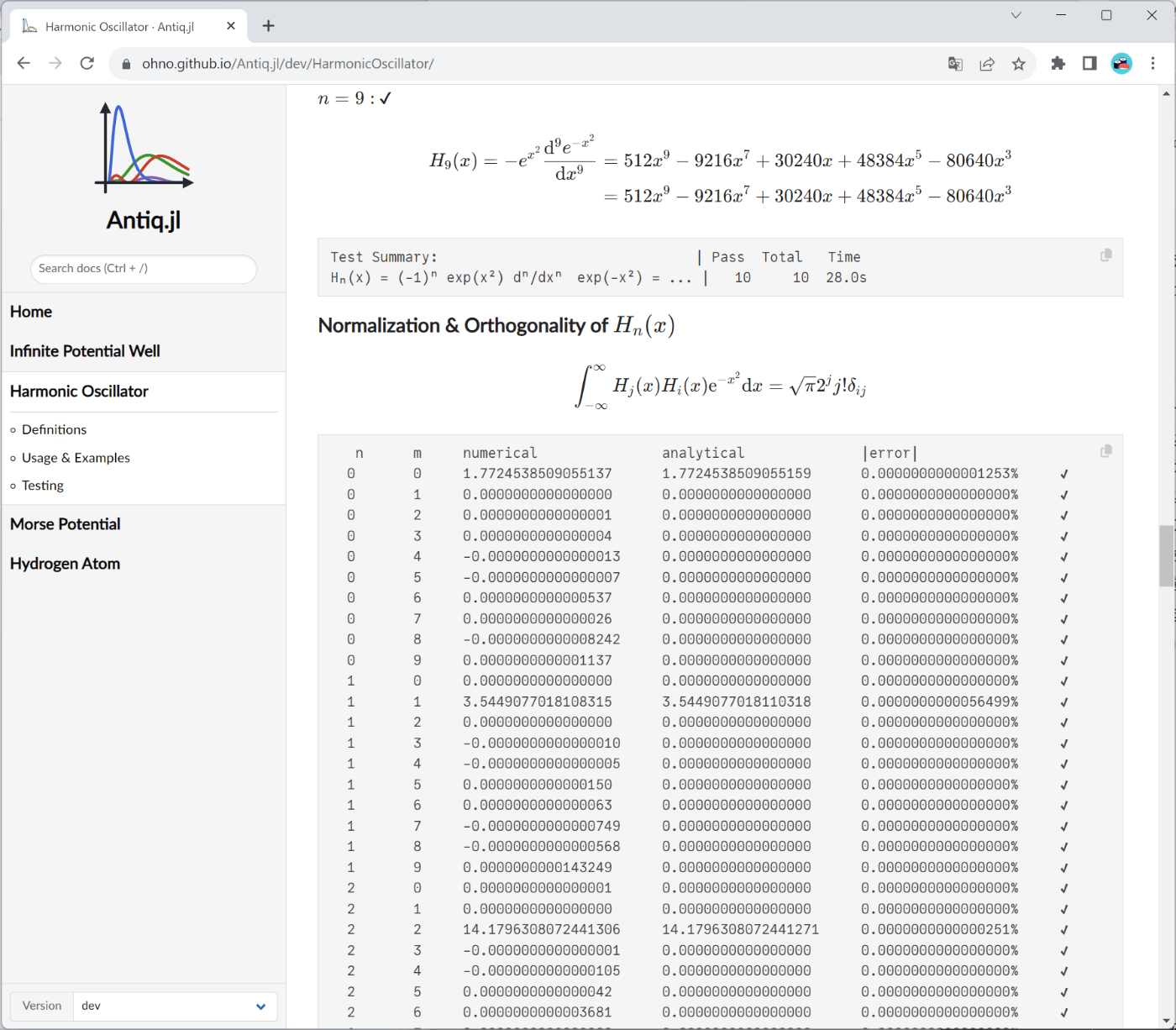
の3点がまとめられています. 例えば, 下記は調和振動子の例です.

ハミルトニアン, 固有値, 固有関数の説明があり, 固有関数に含まれるエルミート多項式の定義と閉形式さらには具体例も紹介しています.

使用方法と具体例もドキュメントにまとめてあります. antique(モデル名, パラメータ)がモジュールを返し, それぞれのモジュールがポテンシャルV(x), 固有値E(), 固有関数ψ(x)を含むので, これらを呼び出して使用します.

テストの実行結果もドキュメントに含まれている点は少々おかしな気もしますが, どのようなテストが行われているか数式も含めて確認できるという点は評価すべき取り組みかと思われます. 次のセクションで紹介します.

テスト技法の紹介

テスト技法の紹介

Juliaの柔軟な型システムによって, 同じ1つのコードに対して数式処理システム（Symbolics.jl）と数値積分（QuadGK.jl）の両方を用いたテストの実行が可能になります. ここでは調和振動子の例を紹介します. 数式処理を用いてエルミート多項式のロドリゲスの公式と閉形式が一致するか検証しており, ドキュメントにも出力結果が含まれます.

エルミート多項式の直交性は数値積分を用いて検証しています：

設計思想 (古いバージョンの話)

設計思想 (古いバージョンの話)

このパッケージでは下記の2つは同じ結果を与えます.

HO = Antique.HarmonicOscillator
@show HO.E(n=0, k=2.0, m=3.0)
@show HO.ψ(0, n=0, k=2.0, m=3.0)

HO = antique(:HarmonicOscillator, k=2.0, m=3.0, ℏ=1.0)
@show HO.E(n=0)
@show HO.ψ(0, n=0)

前者では固有値と固有関数を呼び出す際は毎回パラメータを指定する必要があり, 後者は最初の1回だけですので, できれば後者を使いたいと思っています. 後者はantique(モデル名, パラメータ)を実行することで, モジュールのソースコードを取得し, パラメータを置換してメタプログラミングによって再評価したモジュールを返すように設計されています. 何か設計思想が間違っている気がしますが, コードの美しさもユーザービリティも向上します. 順を追って説明していきますので, まずは調和振動子のモジュールをご覧ください.

module HarmonicOscillator

    # Default
    k = 1.0 # change here!
    m = 1.0 # change here!
    ℏ = 1.0 # change here!

    # Potential
    V(x; k=k, m=m, ω=sqrt(k/m)) = 1/2*k*x^2

    # Energy
    E(; n=0, k=k, m=m, ω=sqrt(k/m), ℏ=ℏ) = ℏ*ω*(n+1/2)

    # Wave Function
    function ψ(x; n=0, k=k, m=m, ω=sqrt(k/m), ℏ=ℏ)
        A = sqrt(1/(factorial(n)*2^n)*sqrt(m*ω/(π*ℏ)))
        ξ = sqrt(m*ω/ℏ) * x
        return A*H(ξ,n=n)*exp(-ξ^2/2)
    end

    # Hermite polynomials
    H(x; n=0) = factorial(n) * sum(m -> (-1)^m // (factorial(m)  * factorial(n-2*m)) * (2*x)^(n-2*m), 0:Int(floor(n/2)))

end

このように, 系を指定するパラメータ（調和振動子ならk, m, ℏ）とその固有値E()・固有関数ψ()を１つのモジュールにまとめています. Pythonだと, クラス内のパラメータを参照したメソッドを定義し, パラメータを変えたインスタンスを生成すれば良いのですが, Juliaにはクラスの概念がないため, モジュールのパラメータを可変にするか, 構造体にメソッドをもたせるかで悩みました（そもそもクラスを使いたくなる時点でJuliaの設計思想に反しているのでは？という気もします）. 構造体にメソッドを持たせるのはかなり大変そうなので, モジュールのパラメータを可変することにしました. パラメータを変える場合, 変更できないことはありませんが, パラメータの異なる2つの系を保持することができません. 具体的にはドキュメントのExamples：

julia> H = antique(:HydrogenAtom, Z=1)
julia> H.E(n=1)
-0.5

julia> He⁺ = antique(:HydrogenAtom, Z=2)
julia> He⁺.E(n=1)
-2.0

で使用している通り, 水素原子とヘリウムイオンのようなパラメータの異なる2つのモジュールを共存させることができないのです. そこで, ソースコード内のchange here!の部分を置換し, 異なるモジュールとして再評価eval()するというアプローチを取っています. しかし, このアプローチの問題としてモジュールがAntique内ではなくBase.Metaに作られてしまうため, 依存関係のパッケージ（モースポテンシャルのみSpecialFunctions.jlのガンマ関数に依存）が読み込まれないという問題があります. SpecialFunctions.jlがインストールされていない場合,

MO = antique(:MorsePotential, μ=1.0, k=1.0, ℏ=1.0)

がエラーとなってしまうので,

MO = Antique.MorsePotential
MO.μ = 1.0
MO.k = 1.0
MO.ℏ = 1.0

を代わりに使用する必要があります. この依存関係の読み込みの問題は今後の課題としています. より良い設計があればご提案をお願いいたします.

追伸

v0.1.1をリリースしました！
https://github.com/JuliaRegistries/General/pull/97810

v0.5.1をリリースしました！
https://ohno.github.io/Antique.jl/v0.5.1/

Discussion