🔍

【ネットワークの中心性】vol.4 次数中心性

2023/09/16に公開

network

シリーズの目次

ネットワーク上で中心的な人物は？

ここまで【ネットワークの中心性】と冠して連載を書いてきましたが，線形代数とグラフ理論の説明ばかりで，ずっと数学的な準備に費やしてきました．本記事からいよいよその応用であるネットワークの中心性，正しくはネットワーク上のノードの中心性について考えていきます．

あるネットワークデータが手に入ったとき，次数分布を見て全体的な構造を確認するマクロ的な分析以外にも，個々のノードがネットワークの中でどの程度中心的（重要）であるかを考えるミクロ的な分析をしたい場合があります．その定量的な指標を中心性指標 (centrality measure) といいます．ネットワーク上で中心的な役割を果たすノードを特定することは，SNSにおけるインフルエンサーやサプライチェーンにおけるキープレイヤーの特定など，様々な場面で応用することができます．

中心性の2つの考え方

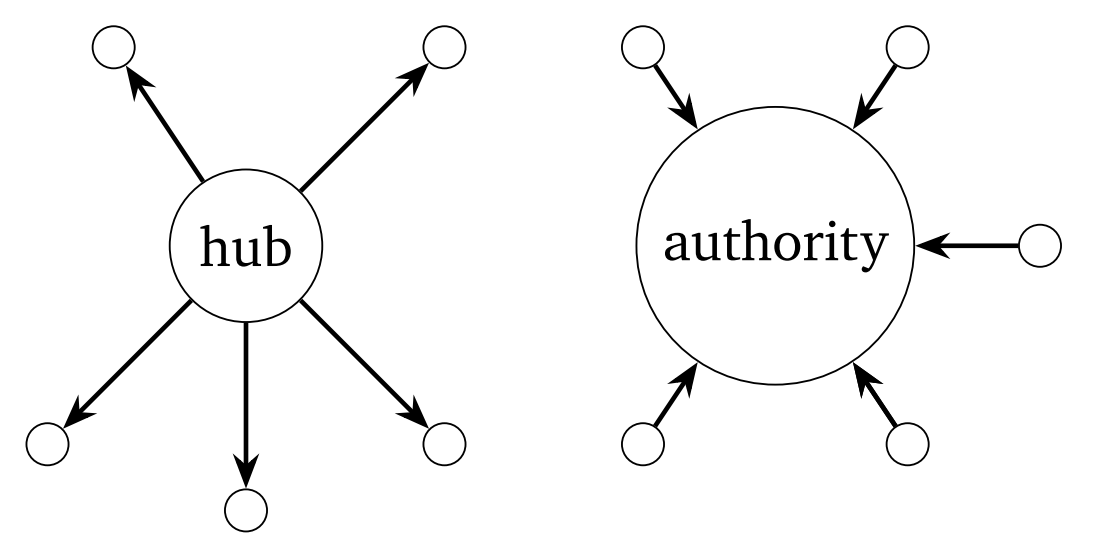
図1：ハブ中心性（左）とオーソリティ中心性（右）
出所）Stachurski et al. (2022)

有向グラフでは，2つの評価軸を持つ中心性を考えることができます．ハブ中心性 (hub centrality) とオーソリティ中心性 (authority centrality) です．ハブ中心性は，どれだけ多くのノードにリンクを張っているかという外向きのつながりを評価し，オーソリティ中心性は，どれだけ多くの他のノードからリンクが張られているかという内向きのつながりを評価します．

たとえば，ニュースまとめサイトやレビュー論文（総説論文）はハブ中心性で，信頼性のある報道機関のウェブサイトやある分野の嚆矢となった論文などはオーソリティ中心性で高く評価されるでしょう．このような引用関係からなるネットワークにおいては，オーソリティは関心のあるトピックに関する有益な情報を含むノードで，ハブは最良のオーソリティがどこにあるかを教えてくれるノードとなります．

同様の考え方は、経済のネットワークでも応用されています．たとえば，イベントの開催や施設の建設などが，経済に与える影響（経済波及効果）を考える際，産業連関表を用いた分析が行われます．これは生産ネットワークを用いた分析であり，ネットワークにおける高いハブ中心性は上流性 (upstreamness) と関連しています．上流に位置する生産部門は，多くの重要な産業に中間財を供給する傾向があります．逆に、高いオーソリティ中心性は下流性 (downstreamness) と関連し，下流に位置する部門は重要な中間財の買い手と解釈できます．経済波及効果については，次のサイトが参考になります．

https://math-fun.net/20180803/1140/

次数中心性

中心性指標はネットワーク $G(V,E)$ に対応づけられたベクトル $\bm{m}\in\R^{|V|}$ として定義されます．ベクトル $\bm{m} = (m_i)_{i\in V}$ の $i$ 番目の要素 $m_i$ はノード $i$ の中心性を表します．

最も単純で素朴な中心性指標は，次数中心性 (degree centrality) です．自分が何個のノードとつながっているか（何本のエッジを持っているか）がベースにある考え方です．それにエッジの方向性が加わると，何個のノードにリンクを張っているか（出ていくエッジの本数）を評価する出次数中心性 (out-degree centrality) $(k_i^{\text{out}})_{i\in V}$ を考えることができます．逆に，何個のノードからリンクが張られているか（入ってくるエッジの本数）を評価して，入次数中心性 (in-degree centrality) $(k_i^{\text{in}})_{i\in V}$ も考えられます．前回定義した入次数と出次数，隣接行列 $A = (a_{ij})_{n \times n}$ を用いると，有向グラフ $G(V,E),~|V|=n$ において，ノード $i$ の入次数中心性と出次数中心性はそれぞれ次のように定義されます．

\begin{align*} k_i^{\text{out}} &　= |N_G^{\text{out}}(i)| = \sum_{j=1}^na_{ij} \\ k_i^{\text{in}} &= |N_G^{\text{in}}(i)| = \sum_{j=1}^na_{ji} \end{align*}

出次数はノード $i$ から出ていくエッジの本数なので，行についての和をとり，入次数はノード $i$ に入ってくるエッジの本数なので，列についての和をとっています．中心性をベクトルで表記すると，出次数中心性 $\bm{k}^{\text{out}}\in \R^n$ と入次数中心性 $\bm{k}^{\text{in}}\in \R^n$ はそれぞれ，

\begin{align*} \bm{k}^{\text{out}}　&= A\bm{1} \\ \bm{k}^{\text{in}}　&= A^\top\bm{1} \end{align*}

と書けます．ただし， $\bm{1}$ はすべての要素が $1$ のベクトルです．Numpy を使えば次のように計算できます．ただし，Aは隣接行列を表す2次元配列で，Nはノード数です．

import numpy as np
out_degree = A @ np.ones(N) # 出次数
in_degree = A.T @ np.ones(N) # 入次数

なお，無向グラフの場合は，ノード $i$ の次数中心性 $k_i$ と次数中心性ベクトル $\bm{k}\in \R^n$ はそれぞれ，

\begin{align*} k_i　&= \sum_{i=1}^n a_{ij} \\ \bm{k}　&= A\bm{1} = A^\top\bm{1} \end{align*}

となります．

次数中心性の特徴

次数中心性は，次数をそのまま中心性指標にするという非常にシンプルな指標です．ノードの近傍の様子さえわかれば良く，実際の計算も隣接行列の行和，あるいは列和を取るという簡単な操作で行えます．また，定義から分かるように，出次数中心性はハブ中心性で，入次数中心性はオーソリティ中心性となっています．出次数中心性 $\bm{k}^{\text{out}}$ と入次数中心性 $\bm{k}^{\text{in}}$ がそれぞれ $A\bm{1},~A^\top\bm{1}$ と計算できたことは，次の事実を示唆しています．すなわち，ハブ中心性からオーソリティ中心性に変換するには，隣接行列の転置を取りさえすれば良いということです．実際，隣接行列 $A = (a_{ij})$ を転置した $A^\top$ の $(i,j)$ 成分を $\left( A^\top \right)_{ij}=b_{ij}$ とすると，

\begin{align*} \bm{k}^{\text{out}}　 &= \left(\sum_j a_{ij} \right) = A\bm{1} \\ \bm{k}^{\text{in}}　 &= \left(\sum_j a_{ji} \right) = \left(\sum_j b_{ij} \right) = A^\top\bm{1} \end{align*}

であることから確かめられます．直感的には，隣接行列の転置を取ることでエッジの矢印の向きを反転できるので，右から $\bm{1}$ をかけるという操作は変えなくて良いということです．この隣接行列の転置を取ってハブ中心性からオーソリティ中心性に変換するというテクニックは，これ以降の中心性指標でも登場します．

Python による実装

Python で次数中心性を計算する degree_centrality() 関数を作ります．隣接行列の転置を取ってハブベースの次数中心性からオーソリティベースの次数中心性に変換するテクニックを使えば，有向グラフにも無向グラフにも使用できる関数ができます^[1]．

import numpy as np

def degree_centrality(A, authority=False):
    """
    Computes the hub-based (authority-based) degree centrality of A.

    Parameters
    ----------
    A : NumPy ndarray
        Adjacency matrix representation of graph.

    authority : bool (default: False)
        If authority = True, A is replaced by its transpose.

    Returns
    -------
    k : NumPy ndarray
        Degree centrality of A.
    """
    A_temp = A.T if authority else A
    N = len(A_temp)
    return A_temp @ np.ones(N)

前回の記事でも取り上げたネットワークで確かめてみましょう．

図2：無向グラフの隣接行列（左）と有向グラフの隣接行列（右）
出所）Menczer et al. (2020)

# 無向グラフの隣接行列
A = np.array([[0, 0, 1, 1],
              [0, 0, 1, 1],
              [1, 1, 0, 1],
              [1, 1, 1, 0]])

degree_centrality(A, authority=False) # >>> array([2., 2., 3., 3.])
degree_centrality(A, authority=True) # >>> array([2., 2., 3., 3.])

図2の左の無向グラフで確認すると，各ノードの次数が計算できていることが確認できます．当然のことですが，隣接行列が対称なのでハブベースとオーソリティベースのどちらでも同じ結果になります．

# 有向グラフの隣接行列
A = np.array([[0, 0, 1, 1],
              [0, 0, 0, 1],
              [0, 1, 0, 0],
              [0, 0, 1, 0]])

# 出次数
degree_centrality(A, authority=False) # >>> array([2., 1., 1., 1.])
# 入次数
degree_centrality(A, authority=True) # >>> array([0., 1., 2., 2.])

図2の右の有向グラフで確認すると，出次数と入次数ともに計算できていることが確認できます．

次数中心性の限界

定義上，次数中心性は自分の近傍というローカルな情報しか考慮しません．つまり，自分から1ステップ先までの情報しか使えず，2ステップ以上先がどうなっているかを無視します．すると，たとえば次のような問題が発生します．

ネットワークが完全グラフに近いと役に立たない
辺境の名士と真の名士を区別できない

ネットワークが完全グラフに近い場合

図3：国別の民間銀行間の資金の流れ
出所）Stachurski et al. (2022)

図3は，民間銀行間の資金（貸付）の流れを，貸し手となった国ごとにグループ化して図示したものです．たとえば、日本 (JP) から米国 (US) への矢印は，国際決済銀行 (BIS) によって収集された日本の銀行が米国の全登録銀行に対して保有する総請求額 (aggregate claims) を示しています．各ノードの大きさは，当該ノードに対する他のノードの対外請求額の合計に対応しており，矢印の幅はその矢印が表す対外請求額に比例しています．

この国際的な銀行間ネットワークは，図3が示す通りほとんどすべてのノードの間にエッジが存在する完全グラフに近い構造を持っています．このようなネットワークに対しては，出次数や入次数に基づく中心性指標でノードをランク付けしても，有益な情報は得られません．実際，図4は銀行間ネットワークにおける各国の出次数中心性と入次数中心性を計算したものですが，完全グラフに近い構造のせいで，ほとんどの国で中心性が同じになっています．

図4：銀行間ネットワークの出次数（左）または入次数（右）に基づく次数中心性
出所）Stachurski et al. (2022)

ハブだからといって中心的とは限らない

人間関係を表すネットワークを考えてみましょう．簡単のため，エッジに方向性のない無向グラフだとします．無向グラフにおける次数中心性では，友達が多い人（ハブ）ほどネットワーク上で中心的であることになります．確かに，友達が少ない人よりも友達が多い人の方が存在感はあるので，一見中心性を測るのに良さそうな気がします．ところが，次数中心性では中心的でなさそうな人が中心であると判定されるケースや，本当に中心的な人を正当に評価できないケースがあります．そのようなケースを，以下の簡略化したネットワークで考えてみます．

import graph_tool.all as gt

## 辺境の名士
# エッジリスト
edge_lst = [(0, 1), (0, 2), (0, 3), (1, 4), (1, 5), (2, 6), (2, 7), (3, 8), (3, 9)]

g = gt.Graph(directed=False) # グラフを生成
g.add_edge_list(edge_lst)    # グラフにエッジを追加
pos = gt.sfdp_layout(g) # レイアウトを指定
gt.graph_draw(g, pos=pos, vertex_text=g.vertex_index); # 可視化

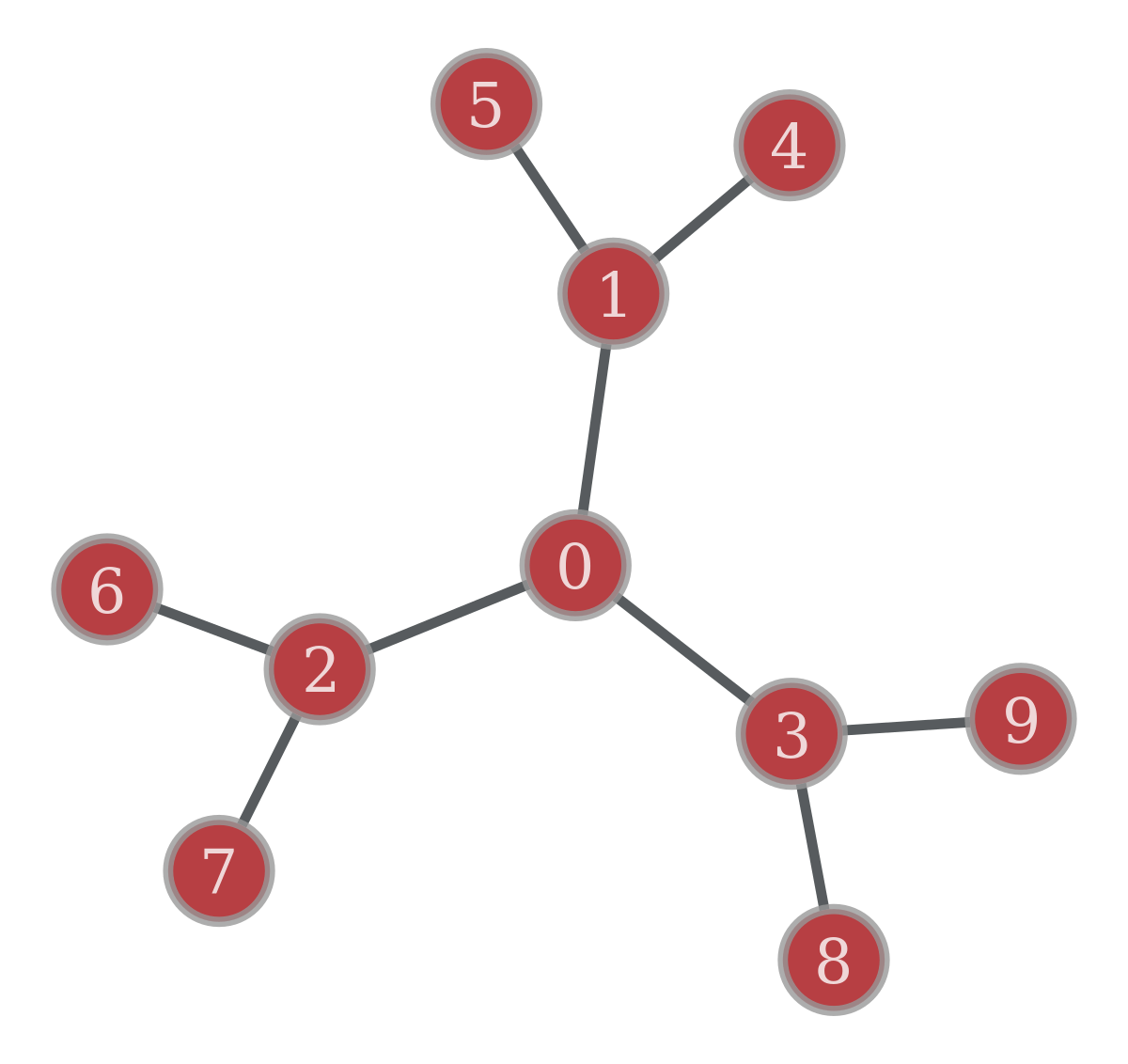
0,1,2,3番のノードの次数はすべて $3$ です．次数中心性で評価すると，これら4つのノードはすべて等しく重要（中心的）であることになります．しかし，ネットワーク全体を見ると，1,2,3番のノードが辺境に位置しているのに対して，0番はそれらをまとめる中心的な位置にあります．たくさんの友達を持つハブであっても，地方という限られた範囲で有名である程度では辺境の名士に過ぎないというわけです^[2]．真の名士は彼ら辺境の名士をまとめる中心的な位置にあって，ネットワーク全体で起きる全国規模の現象にも詳しい0番のような人物です．本当はこのような差異を識別したいのですが，次数中心性だと辺境の名士も真の名士も同じスコアになるどころか，辺境の名士の方が高いスコアを持つケース（e.g., 3番に新たなノード10がつながる場合）が生じてしまいます．

以上をまとめると，次数中心性は自分の近傍のローカルな情報しか扱えず，ネットワーク全体の構造が持つグローバルな情報を無視してしまうため，ノードのランキング機能を果たせない，あるいはノードを正当に評価できないという限界があります．

次回予告

本記事では，ハブ中心性とオーソリティ中心性というネットワークの中心性における2つの概念を紹介し，次数中心性の定義を確認しました．次数中心性はシンプルで計算も楽ですが，計算に自分の近傍の情報しか使わないため，ネットワーク全体の構造を考慮したスコアリングができないという限界があることを確認しました．

次回第5回は，ネットワーク構造というグローバルな情報を使って中心性を計算できるのかという問題に対処した固有ベクトル中心性を見ていきます．

参考文献

John Stachurski and Thomas J. Sargent. Economic Networks: Theory and Computation (QuantEcon, 2022). URL https://networks.quantecon.org/ .
Menczer, F., Fortunato, S. & Davis, C. A. A First Course in Network Science (Cambridge University Press, 2020). URL https://cambridgeuniversitypress.github.io/FirstCourseNetworkScience/.
増田直紀(2007)『私たちはどうつながっているのか：ネットワークの科学を応用する』，中央公論新社（中公新書）

脚注

無向グラフの隣接行列は対称行列なので，行和と列和は一致します．つまり，無向グラフの場合はどちらを使用しても良いということです． ↩︎
ネットワーク上の「辺境の名士」という表現は増田(2007)から拝借しました．直感的にイメージしやすいため，筆者は好んで使っています． ↩︎

GitHubで編集を提案