【ネットワークの中心性】vol.6 Katz 中心性

シリーズの目次

1. Introduction
2. 線形代数
3. グラフ理論
4. 次数中心性
5. 固有ベクトル中心性
6. Katz 中心性
7. PageRank

枝をたくさん張っても点がもらえない...

図1：強連結でない有向グラフ

前回の記事では，次数中心性を固有ベクトル中心性に拡張することで，ネットワーク構造の持つグローバルな情報を反映したランク付けが達成できることを確認しました．しかし，図1のような強連結でない有向グラフでは，エッジを張っているにもかかわらず，定義上中心性が $0$ と判定されてしまうノードが存在することがわかりました．

この問題をシンプルなアイデアで解決するのが Katz 中心性 (Katz centrality) です^[1]．問題の元凶は，$i$ さんが $j$ さんに枝を張っていても，$j$ さんの中心性 $e_j$ が $0$ であるとき，$i$ さんは点をもらえない（$a_{ij}e_j=1\cdot 0=0$）ことにあるのでした．それなら，最初から皆に等しく点をあげておけば良いじゃないかというのが基本的なアイデアです．

Katz 中心性

Katz 中心性は固有ベクトル中心性の欠点を補完したものなので，ハブベース固有ベクトル中心性からハブベース Katz 中心性 (hub-based Katz centrality) を，オーソリティベース固有ベクトル中心性からオーソリティベース Katz 中心性 (authority-based Katz centrality) をそれぞれ導けます．参考にハブベース固有ベクトル中心性 $e_i$ とオーソリティベース固有ベクトル中心性 $\varepsilon_j$ の定義を再掲します．

$$\begin{align*} e_i = \frac{1}{\rho(A)}\sum_{j=1}^{n} a_{ij}e_j~~~~~~~~\forall i = 1,\dots,n \\ \varepsilon_j = \frac{1}{\rho(A)}\sum_{i=1}^{n} a_{ij}\varepsilon_i~~~~~~~~\forall j = 1,\dots,n \end{align*}$$

以下，有向グラフ $G(V,E),|V|=n$ を考え，$A = (a_{ij})_{n \times n}$ を $G$ の隣接行列とします．ノード $i$ のハブベース Katz 中心性を $\kappa_i$ とし，それを要素に持つベクトルを $\bm{\kappa} \in \R^n$，ノード $j$ のオーソリティベース固有ベクトル中心性を $\kappa_j$ とし，それを要素に持つベクトルを $\bm{\kappa} \in \R^n$ と表記します．

ハブベース Katz 中心性

ノード $i$ のハブベース Katz 中心性 $\kappa_i$ は，$\alpha,~\beta$ を正の定数として

$$\begin{align} \kappa_i = \alpha\sum_{j=1}^{n} a_{ij}\kappa_j+\beta~~~~~~~~\forall i = 1,\dots,n \end{align}$$

と定義されます．ただし，$\alpha \in (0, \rho(A)^{-1})$ と仮定します．$\rho(A)$ は $A$ のスペクトル半径です．$(1)$ 式の右辺第1項は固有ベクトル中心性の定義そのままです．第2項の $\beta$ があらかじめ皆に割り振っておく点数です．このように定義することで，出次数が $0$ のノード（シンク）も $\beta$ のスコアを持つことになり，他のノードにエッジを張ったとき，それがたとえシンクであっても点がもらえることが保証されます．

ところで， $\beta$ は正の定数であれば良いので，簡単のため $\beta=1$ とします．すると $(1)$ 式は

$$\begin{align} \kappa_i = \alpha\sum_{j=1}^{n} a_{ij}\kappa_j+1~~~~~~~~\forall i = 1,\dots,n \end{align}$$

と書け，さらにこれをベクトル形式で書くと，$\bm{1}\in\R^n$ を全ての要素が $1$ のベクトルとして

$$\begin{align} \bm{\kappa} = \alpha A\bm{\kappa} + \bm{1} \iff \left(I-\alpha A\right)\bm{\kappa} = \bm{1} \end{align}$$

と変形できます．何となくノイマン級数の補題で見たような形をしていますね．というのは，$I-\alpha A$ が正則で逆行列 $\left(I-\alpha A\right)^{-1}$ を持てば，ハブベース Katz 中心性 $\bm{\kappa}$ は一意に定まります．実際，$\alpha \in (0, \rho(A)^{-1})$ の仮定から $\bm{\kappa}\in\R^n_{++}$ は常に有限で一意に決まり，

$$\begin{align} \bm{\kappa} = \left(I-\alpha A\right)^{-1}\bm{1} = \sum_{m=0}^\infty (\alpha A)^m \bm{1} \end{align}$$

で与えられます．

証明

$\rho(\alpha A)=\alpha\rho(A)$ より，$0 < \alpha < \rho(A)^{-1}$ の仮定から $\rho(\alpha A)<1$ が成立する．このときノイマン級数の補題より $I-\alpha A$ は正則で

$$\left(I-\alpha A\right)^{-1} = \sum_{m=0}^\infty (\alpha A)^m$$

が成り立つ．したがって，線形システム $(3)$ の解は

$$\begin{align*} \bm{\kappa} &= \left(I-\alpha A\right)^{-1}\bm{1} \\ &= \sum_{m=0}^\infty (\alpha A)^m \bm{1} \\ &= \bm{1} + \sum_{m=1}^\infty (\alpha A)^m \bm{1} &\geqslant \bm{1} \end{align*}$$

で与えられる．

オーソリティベース Katz 中心性

ノード $j$ のオーソリティベース Katz 中心性 $\kappa_j$ は，$\alpha,~\beta$ を正の定数として

$$\begin{align} \kappa_j = \alpha\sum_{i=1}^{n} a_{ij}\kappa_i+\beta~~~~~~~~\forall j = 1,\dots,n \end{align}$$

と定義されます．ただし，$\alpha \in (0, \rho(A)^{-1})$ と仮定します．先ほどと同様，右辺第1項は固有ベクトル中心性の定義そのままです．第2項の $\beta$ があらかじめ皆に割り振っておく点数です．このように定義することで，入次数が $0$ のノード（ソース）も $\beta$ のスコアを持つことになり，他のノードからエッジが張られたとき，それがたとえソースであっても点がもらえることが保証されます．

$\beta$ は正の定数であれば良いので，簡単のため $\beta=1$ とします．すると $(5)$ 式は

$$\begin{align} \kappa_j = \alpha\sum_{i=1}^{n} a_{ij}\kappa_i+1~~~~~~~~\forall j = 1,\dots,n \end{align}$$

と書け，さらにこれをベクトル形式で書くと

$$\begin{align} \bm{\kappa} = \alpha A^\top\bm{\kappa} + \bm{1} \iff \left(I-\alpha A^\top\right)\bm{\kappa} = \bm{1} \end{align}$$

と変形できます．$I-\alpha A^\top$ が正則で逆行列 $\left(I-\alpha A^\top\right)^{-1}$ を持てば，オーソリティベース Katz 中心性 $\bm{\kappa}$ は一意に定まります．実際，$\alpha \in (0, \rho(A)^{-1})$ の仮定から $\bm{\kappa}\in\R^n_{++}$ は常に有限で一意に決まり，

$$\begin{align} \bm{\kappa} = \left(I-\alpha A^\top\right)^{-1}\bm{1} \iff \bm{\kappa}^\top = \bm{1}^\top \left(I-\alpha A\right)^{-1} \end{align}$$

で与えられます．

証明

$0 < \alpha < \rho(A)^{-1}$ の仮定から $\alpha\rho(A)<1$．$\rho(\alpha A)=\alpha\rho(A)$ であることと $\rho(A) = \rho(A^\top)$ より $\rho(\alpha A^\top)<1$ が成立する．このときノイマン級数の補題より $I-\alpha A^\top$ は正則で逆行列 $\left(I-\alpha A^\top\right)^{-1}$ が存在する．したがって，線形システム $(7)$ の解は

$$\bm{\kappa} = \left(I-\alpha A^\top\right)^{-1}\bm{1}$$

で与えられる．また，両辺の転置をとると

$$\begin{align*} \bm{\kappa}^\top &= \bm{1}^\top\left[\left(I-\alpha A^\top\right)^{-1}\right]^\top \\ &= \bm{1}^\top\left[\left(I-\alpha A^\top\right)^\top\right]^{-1} \\ &= \bm{1}^\top\left(I-\alpha A^\top\right)^{-1}. \end{align*}$$

パラメータ $\alpha$ の役割

パラメータ $\alpha$ は減衰パラメータ (attenuation parameter) であり，$\alpha \in (0, \rho(A)^{-1})$ の条件のもとで $\bm{\kappa}$ が有限かつ一意に定まることを保証します．ネットワークが強連結であれば，$\alpha \to \rho(A)^{-1}$ としたときハブ／オーソリティベース Katz 中心性は，ハブ／オーソリティベース固有ベクトル中心性に収束することが知られています^[2]．次数中心性の回で登場した国際的な銀行間ネットワークの中心性を表す図2で，Katz 中心性と固有ベクトル中心性の分布が似通っているのはそのためです．

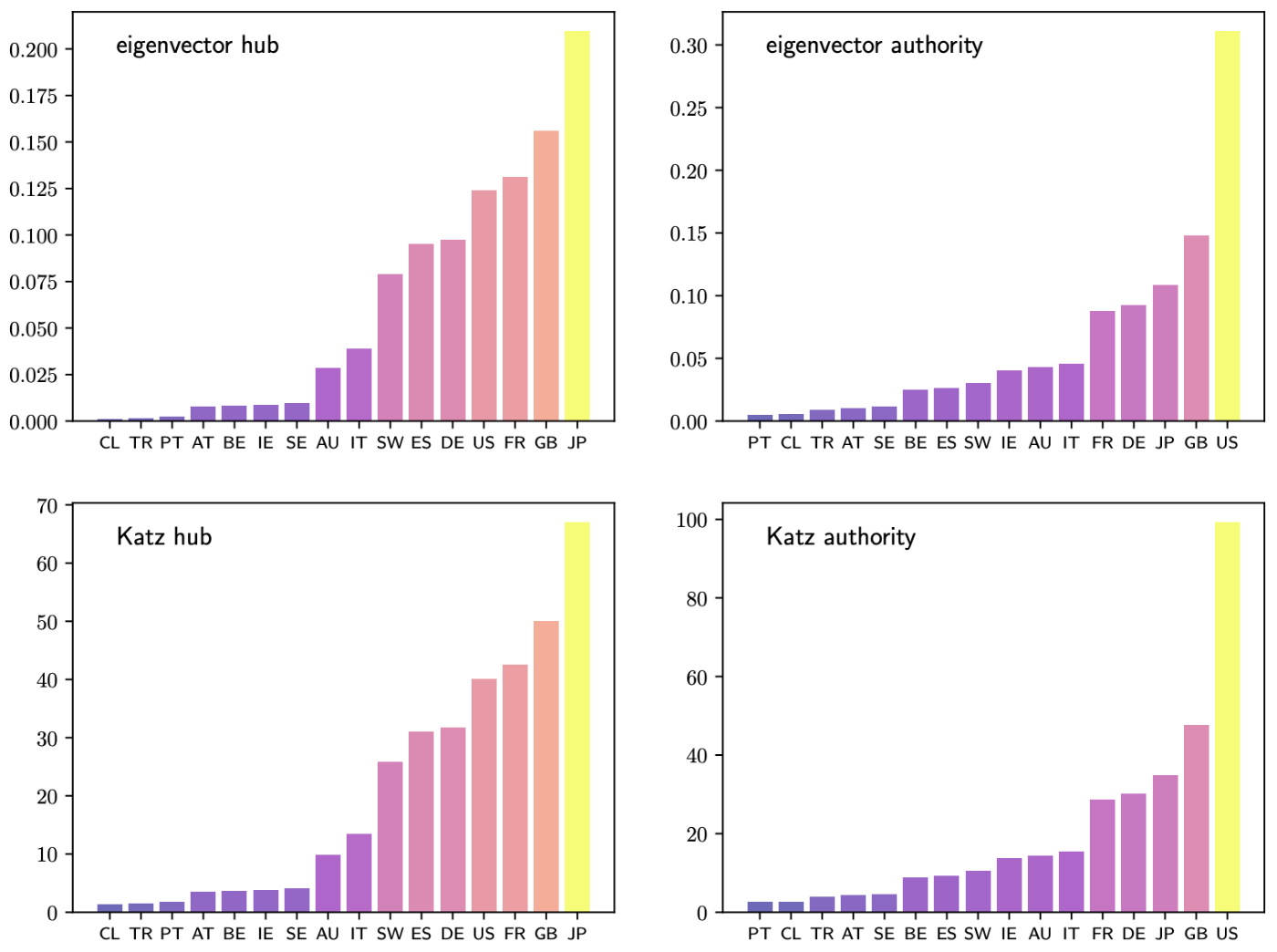
図2：ハブ／オーソリティベース固有ベクトル中心性（上段）とハブ／オーソリティベース Katz 中心性（下段）
出所）Stachurski et al. (2022)

実際の計算においては，$0<\alpha<\rho(A)^{-1}$ の範囲で $\alpha$ は任意に取れますが，$\rho(A)<1$ のときは $\alpha = 1$ とするのがデフォルトとされています．

Python による実装

Katz 中心性を計算する katz_centrality() 関数を作り，図1の有向グラフの中心性を求めます．例の如く，隣接行列の転置を取ってハブ中心性からオーソリティ中心性に変換するテクニックを使って，有向グラフにも無向グラフにも使用できる関数にしておきます．まず，隣接行列 $A$ のスペクトル半径 $\rho(A)$ を計算する spectral_radius() 関数を定義します．

import numpy as np

def spectral_radius(M):
    """
    Compute the spectral radius of M.
    """
    return np.max(np.abs(np.linalg.eigvals(M)))

$\rho(A)$ を計算して，$\rho(A)<1$ の場合は $\alpha = 1$ をデフォルトにし，$\rho(A)\geqslant 1$ の場合は $0<\alpha<\rho(A)^{-1}$ の範囲で任意に取ることにします．

def katz_centrality(A, alpha=1, authority=False):
    """
    Computes the Katz centrality of A, defined as the x solving

    x = 1 + alpha A x    (1 = vector of ones)

    Parameters
    ----------
    A : NumPy ndarray
        Adjacency matrix representation of graph.

    alpha : int or float (default: 1)
        When the spectral radius of A < 1, using alpha = 1 is default.

    authority : bool (default: False)
        If authority = True, A is replaced by its transpose.

    Returns
    -------
    k : NumPy ndarray
        Katz centrality of A.
    """
    A_temp = A.T if authority else A
    n = len(A_temp)
    I = np.identity(n)
    r = spectral_radius(A_temp)
    alpha = np.random.uniform(low=0.0, high=1/r) if r >= 1 else alpha
    IA_inv = np.linalg.inv(I - alpha * A_temp)
    return IA_inv @ np.ones(n)

図1の有向グラフをgraph-toolで生成します．

import graph_tool.all as gt

edge_lst = [(0, 1), (0, 2), (0, 3), (1, 2)] # エッジリスト
g = gt.Graph(directed=True) # グラフを生成
g.add_edge_list(edge_lst)    # グラフにエッジを追加
gt.graph_draw(g, vertex_text=g.vertex_index, output_size=(300, 300));  # グラフを可視化

グラフ g を隣接行列 (numpy.ndarray) に変換して，katz_centrality() 関数に渡します．次数の計算は，第4回で定義した degree_centrality() 関数を使用しています．

import pandas as pd

# グラフを隣接行列に変換
A = gt.adjacency(g).toarray().T # graph-tool の隣接行列の定義は j --> i で a_{ij} = 1

out_degree = degree_centrality(A) # 出次数
in_degree = degree_centrality(A, True) # 入次数

katz_hub = katz_centrality(A, authority=False) # ハブベース Katz 中心性
katz_authority =  katz_centrality(A, authority=True) # オーソリティベース Katz 中心性

# データフレームにまとめる
df = pd.DataFrame({"out_degree": out_degree, 
                     "katz_hub": katz_hub, 
                     "in_degree": in_degree, 
                     "katz_authority": katz_authority})
df

index	out_degree	katz_hub	in_degree	katz_authority
0	3.0	5.0	0.0	1.0
1	1.0	2.0	1.0	2.0
2	0.0	1.0	2.0	4.0
3	0.0	1.0	1.0	2.0

固有ベクトル中心性では中心性はすべて $0$ でしたが，ハブベース Katz 中心性ではハブである0番のノードが最も高く評価され，オーソリティベース中心性ではオーソリティである2番のノードが最も高く評価されました．Katz 中心性によって固有ベクトル中心性の問題を解決できることがわかります．

Katz 中心性の問題点

Katz 中心性にもまた，問題点があります．Katz 中心性の高いノードが1つあると，それに隣接するノードの中心性も無条件に高くなってしまいます．簡単のため，無向グラフで考えます．仮に高い Katz 中心性をもつノード $i$ さんが100個のノードとつながっているとき，定義上それら100個のノードは，自身の中心性の計算に $i$ さんの高い Katz 中心性をそのまま加えることができます．つまり，$i$ さんの高い中心性が，100個のノードすべてに等しく伝播してしまい，結果として100個のノードもまた高い中心性を獲得するということです．

たとえば，楽天市場のような総合的なショッピングサイトの中心性は非常に高くなるでしょう．楽天市場はたくさんのメーカーや販売者のウェブページにリンクしています．つまり，楽天市場は膨大な数の外部につながるエッジを持つわけですが，このとき楽天市場の持つ非常に高い中心性が等しくすべての外部サイトに流入するのは適切と言えるでしょうか．おそらくほとんどの人は，個々の外部サイトに流入する楽天市場の中心性は何らかの方法で薄められるべきだと考えるでしょう．しかし，Katz 中心性によれば楽天市場の中心性はそっくりそのまま外部サイトに流入しても構わないというのです．

次回予告

本記事では，Katz 中心性の定義と特徴を確認し，Python で無向グラフ（有向グラフ）の（ハブ／オーソリティベース）Katz 中心性を計算する katz_centrality() 関数を実装しました．実装した関数を使えば，固有ベクトル中心性が使えない有向グラフに対しても中心性を計算できることを確認し，Katz 中心性は固有ベクトル中心性の問題点を解決していることがわかりました．しかしKatz 中心性には，中心性の高いノードに隣接するノードの中心性もすべて等しく高くなるという望ましくない性質があることが懸念点として挙げられました．

次回第7回は，Katz 中心性の問題点を解決するアプローチである PageRank を見ていきます．元論文 Brin and Page (1998) では，グラフ上のランダムウォークとして導入されていますが，本連載は次数中心性を拡張していくスタイルなので，次回も Katz 中心性を拡張する形で議論を進めていきます．

おまけ

前回，固有ベクトル中心性はネットワーク全体の情報を使って計算される中心性指標であることを確認しました．固有ベクトル中心性の拡張である Katz 中心性もまた，ネットワーク全体の情報を使用しているのですが，ここでは別の方法でそれを確かめてみます．個人的にはこちらの方が直感的に理解できて良いなと思っています．

Katz 中心性 $\bm{\kappa}$ は次式で与えられるのでした．

$$\bm{\kappa} = \left(I-\alpha A\right)^{-1}\bm{1} = \sum_{m=0}^\infty (\alpha A)^m \bm{1}$$

べき級数の和の部分を展開すると，

$$\begin{align*} \bm{\kappa} &= \sum_{m=0}^\infty (\alpha A)^m \bm{1} \\ &= \left(I + \alpha A + \alpha^2 A^2 + \alpha^3 A^3 \cdots \right)\bm{1} \\ &= \bm{1} + \alpha A\bm{1} + \alpha^2 A^2\bm{1} + \alpha^3 A^3\bm{1} \cdots \end{align*}$$

と書けます．このように展開すると，それぞれの項で隣接行列のべき乗の行和を取って足し合わせていることがわかります．ところで，隣接行列のべき乗 $A^m$ は，ざっくり言うと $m$ ステップでつながっているノードのペアを記述するものでした^[3]．$m=0$ から $\infty$ までの各 $m$ ステップでのつながりを表す行列を使って計算しているということは，ネットワーク全体のつながりの情報を使って中心性を計算していることに他なりません．$\rho(A)<1$ の時は $\alpha=1$ とデフォルトで設定するので，$\alpha$ については考えなくて良くなります．$\rho(A)\geqslant 1$ の時は $\alpha$ は $0<\alpha<\rho(A)^{-1}$ の範囲で任意にとりますが，その場合は $m \to \infty$ で $\alpha^m \to 0$ になるので，$m$ ステップでつながっていても遠くなるにつれて，中心性への寄与が減衰するようになっており，うまいことできてるなと感心します．

参考文献

• Benzi, Michele, and Christine Klymko. "On the limiting behavior of parameter-dependent network centrality measures." SIAM Journal on Matrix Analysis and Applications 36.2 (2015): 686-706.
• Bonacich, P. (1987). Power and centrality: A family of measures. American journal of sociology, 92(5), 1170-1182.
• Brin, S., & Page, L. (1998). The anatomy of a large-scale hypertextual web search engine. Computer networks and ISDN systems, 30(1-7), 107-117.
• John Stachurski and Thomas J. Sargent. Economic Networks: Theory and Computation (QuantEcon, 2022). URL https://networks.quantecon.org/ .
• Katz, L. (1953). A new status index derived from sociometric analysis. Psychometrika, 18(1), 39-43.
• Menczer, F., Fortunato, S. & Davis, C. A. A First Course in Network Science (Cambridge University Press, 2020). URL https://cambridgeuniversitypress.github.io/FirstCourseNetworkScience/.

脚注

1. 最初に Katz(1953) が提唱したため Katz 中心性と呼ばれていますが，その後の Bonacich(1987) による精緻化を評価して Bonacich 中心性，あるいは Katz-Bonacich 中心性と呼ばれることもあります．

2. 証明は Benzi and Klymko (2015) を参照してください．

3. 詳細は第3回を参照してください．