【ネットワークの中心性】vol.7 PageRank

シリーズの目次

1. Introduction
2. 線形代数
3. グラフ理論
4. 次数中心性
5. 固有ベクトル中心性
6. Katz 中心性
7. PageRank

虎の威を借る狐

前回の記事では， Katz 中心性は固有ベクトル中心性の欠点を補完する一方で，高い中心性を持つノードに隣接するノードに同等のスコアが流入してしまうという問題があることを指摘しました．Katz 中心性の定義だと，自身のフォロワーは少ないのにインフルエンサーからフォローされることで中心性が高くなるという「虎の威を借る狐」のような状況が生まれてしまいます．もちろん，インフルエンサーがそのユーザーだけをフォローしている場合はその限りではありません．しかし多くの場合，インフルエンサーは多数のユーザーをフォローしているため，フォローされている個々のユーザーは "one of them" であることは珍しくないでしょう．Katz 中心性に対して，中心性の高いノードの近傍にあるノードは "one of them" であるという性質を組み込んだのが PageRank （ページランク）です^[1]．

Google の検索技術 PageRank

PageRank は，Google の共同創設者であるラリー・ペイジ (Larry Page) とセルゲイ・ブリン (Sergey Brin) が World Wide Web (WWW) を対象とする検索エンジンが直面していた問題を解決するために開発したウェブページのスコアリング指標です [Brin and Page, 1998]．ユーザがクエリを入力すると，クエリに関係のある膨大な数のページが見つかりますが，どのページがユーザにとって有益な情報なのかを特定することは困難でした．ペイジとブリンはこの問題を解決するべく，WWW のハイパーリンク構造を利用してウェブページの重要性をスコアリングするアルゴリズム PageRank を考案しました．PageRank は Google の初期の成功の一因となったとされています．

PageRank はたくさんのウェブページからリンクされているページほど重要であるとみなすオーソリティ中心性です．ですので，Katz 中心性から PageRank への拡張を行うにあたって，オーソリティベース Katz 中心性を拡張することを考えます．復習ですが，ノード $j$ のオーソリティベース Katz 中心性 $\kappa_j$ は次のように定義されるのでした．

$$\begin{align} \kappa_j = \alpha\sum_{i=1}^{n} a_{ij}\kappa_i+\beta~~~~~~~~\forall j = 1,\dots,n \end{align}$$

ただし，$\alpha,~\beta$ は正の定数で，特に $\alpha \in (0, \rho(A)^{-1})$ を仮定します． $\rho(A)$ は $A$ のスペクトル半径です．

PageRank の定義

以下，有向グラフ $G(V,E),|V|=n$ を考え，$A = (a_{ij})_{n \times n}$ を $G$ の隣接行列とします．ノード $j$ の PageRank を $p_j$ とし，それを要素に持つベクトルを $\bm{p} \in \R^n$ と表記します．

以下の議論は，主に Newman(2018) に立脚しています． Newman(2018) では，隣接行列 $A=(a_{ij})$ の定義が，ノード $j$ から $i$ にエッジが張られているとき $a_{ij}=1$，そうでなければ $a_{ij}=0$ となっており，本連載と逆になっていることに注意してください．

先ほど中心性の高いノードの近傍にあるノードは "one of them" であるという話をしました．インフルエンサーである $i$ さんが $j$ さんをフォローしていれば，$j$ さんは $i$ さんのおかげでフォロワー数が $1$ 増えますが，$i$ さんがたくさんのユーザーをフォローしていれば，$i$ さんにとって $j$ さんの重要性は相対的に低くなります．

WWW 上のウェブページにも全く同じことが言えます．ページ $i$ からページ $j$ にハイパーリンクが張られていれば，ノード $j$ は $i$ から入次数を1つ獲得することになりますが，ページ $i$ の出次数が多ければ，ページ $i$ にとって $j$ の重要性は相対的に低くなります．逆に，入次数の大きい重要なノード $j$ が $i$ にだけハイパーリンクを張っていれば，$j$ の重要性はそっくりそのまま $i$ に推移することになります．

Katz 中心性の拡張

では Katz 中心性をどのように拡張すれば，相手は自分の出次数によって "one of them" にも "only one" にもなりえるという性質を反映できるでしょうか．ノード $i$ から $j$ に流入する $i$ の中心性 $p_i$ を出次数 $k_i^{\text{out}}$ で割り引けば良さそうです．すなわち，$\alpha,~\beta$ を正の定数として，

$$\begin{align} p_j = \alpha\sum_{i=1}^{n} a_{ij}\frac{p_i}{k_i^{\text{out}}}+\beta~~~~~~~~\forall j = 1,\dots,n \end{align}$$

となります．$a_{ij}=1$ かつ $k_i^{\text{out}}=1$ のときは，ノード $j$ は $i$ にとって "only one" な相手ですから， $i$ に $p_i$ がそのまま推移します．$a_{ij}=1$ かつ $k_i^{\text{out}}\geqslant 2$ のときは，$j$ は $i$ にとって "one of them" なので， $p_i$ が $k_i^{\text{out}}$ の分だけ割り引かれてノード $i$ に推移します．

これは一見良さそうな定義ですが，$k_i^{\text{out}}=0$ の場合に問題が生じます．$k_i^{\text{out}}=\sum_{j=1}^na_{ij}=0$ のときは $a_{ij}=0~~\forall j$ ですから，$(2)$ 式の対応する項が $0/0$ となって定義できません．分母が $0$ になるのが問題なので，$k_i^{\text{out}}$ ではなく $\max(1,~k_i^{\text{out}})$ で割り引くことで対処します．すると，ノード $j$ の PageRank は，

$$\begin{align} p_j = \alpha\sum_{i=1}^{n} a_{ij}\frac{p_i}{\max(1,~k_i^{\text{out}})}+\beta~~~~~~~~\forall j = 1,\dots,n \end{align}$$

と定義されます．こうすることで $k_i^{\text{out}}=0$ の場合でも定義可能で，その際は $a_{ij}=0$ の部分が，ノード $j$ にリンクを張っていないノードの $p_j$ への寄与はないことを保証します．$(3)$ 式をベクトル形式で書くと，$\bm{p}=(p_j)_{j\in V}$ は

$$\begin{align} \bm{p} = \alpha A^\top D^{-1}\bm{p} + \beta\bm{1} \end{align}$$

となります．ただし，$D=\text{diag}\left(\max(1,~k_i^{\text{out}})\right)$ で，$\bm{1}\in\R^n$ は全ての要素が $1$ のベクトルです．さらに，$M \equiv A^\top D^{-1}$ とおけば $(4)$ 式は

$$\begin{align} \left(I-\alpha M\right)\bm{p} = \beta\bm{1} \end{align}$$

と変形できます．$I-\alpha M$ が正則で逆行列 $\left(I-\alpha M\right)^{-1}$ を持てば，PageRank $\bm{p}$ は一意に定まります．実際，$\alpha \in (0, \rho(M)^{-1})$ を仮定すると $\bm{p}\in\R^n_{++}$ は常に有限で一意に決まり，

$$\begin{align} \bm{p} = \beta\left(I-\alpha M\right)^{-1}\bm{1} \end{align}$$

で与えられます．

証明

$\rho(\alpha M)=\alpha\rho(M)$ より，$0 < \alpha < \rho(M)^{-1}$ の仮定から $\rho(\alpha M)<1$ が成立する．このときノイマン級数の補題より $I-\alpha M$ は正則で

$$\left(I-\alpha M\right)^{-1} = \sum_{l=0}^\infty (\alpha M)^l$$

が成り立つ．したがって，線形システム $(5)$ の解は

$$\begin{align*} \bm{p} &= \left(I-\alpha M\right)^{-1}\beta\bm{1} \\ &= \sum_{l=0}^\infty (\alpha A)^l \beta\bm{1} \\ &= \beta\bm{1} + \sum_{l=1}^\infty (\alpha A)^l \beta\bm{1} &\geqslant \beta\bm{1} \end{align*}$$

で与えられる．

減衰係数の導入

Katz 中心性の拡張としての PageRank は $(3)$ 式の通りですが，Brin and Page (1998) は，実際のユーザーの行動をモデル化して，減衰係数 (damping factor) なるものを導入しています．Web をブラウジング（ネットサーフィン）する人は最初ランダムにページが与えられ，ハイパーリンクに沿ってページを遷移し続けます．しばらくすると探し物を掘り当てて目的を達成するか，ハイパーリンクに沿った一連のブラウジングに飽きて，再度ランダムに選ばれたページからネットサーフィンを始めます．これをランダムサーファーモデル (random surfer model) といい，このモデルではランダムサーファーがあるページに訪れる確率がその PageRank であると考えます．そして，減衰係数 $d\in(0,1)$ は，それぞれのページにおいてランダムサーファーが飽きて離脱する確率です．実際の減衰係数の値は $d=0.85$ に設定してあるそうです．

ランダムサーファーモデルでは，ユーザーがネットサーフィンに飽きて別のページにランダムにジャンプするため，どのページからもリンクが張られていないページに飛ぶ可能性があります．つまり，どのページも確率的なスコアが与えられるということです．Katz 中心性では皆に等しく $\beta>0$ を与えましたが，ここではランダムサーファーがページにジャンプしてくる確率 $1/N$ を与えましょう．$N$ はページ（ノード）数です．PageRank はランダムサーファーがそのページを訪れる確率なので，グラフ構造由来のスコアと確率的なジャンプによるスコアの加重平均を取ります．ここまでの議論を考慮して，まず $(2)$ 式を書き換えると，

$$\begin{align} p_j = (1-d)\frac{1}{N} + d\sum_{i=1}^{N} a_{ij}\frac{p_i}{k_i^{\text{out}}}~~~~~~~~\forall j = 1,\dots,N \end{align}$$

となります．両辺の $j$ についての和をとると，

$$\begin{align*} \sum_{j=1}^Np_j &= \sum_{j=1}^N\left[(1-d)\frac{1}{N}\right] + \sum_{j=1}^Nd\sum_{i=1}^{N} a_{ij}\frac{p_i}{k_i^{\text{out}}} \\ &= (1-d) + d\sum_{i=1}^{N}\sum_{j=1}^N a_{ij}\frac{p_i}{\sum_{j=1}^N a_{ij}} \\ &= (1-d) + d\sum_{i=1}^{N}p_i \\ \end{align*}$$

左辺の和の添え字を $i$ に変えて整理すると

$$\begin{align*} (1-d)\sum_{i=1}^Np_i = (1-d) \\ \sum_{i=1}^Np_i=1 \end{align*}$$

となり，PageRank が確率として定義できていることが確認できます．先ほどと同様に，$k_i^{\text{out}}=0$ の場合でも定義できるよう $\max(1,~k_i^{\text{out}})$ で割り引いて

$$\begin{align} p_j = (1-d)\frac{1}{N} + d\sum_{i=1}^{N} a_{ij}\frac{p_i}{\max(1,~k_i^{\text{out}})}~~~~~~~~\forall j = 1,\dots,N \end{align}$$

を減衰係数 $d$ を導入したノード $j$ の PageRank とします．PageRank $\bm{p}$ は $(6)$ 式において $\beta=(1-d)/N$ とすれば，

$$\begin{align} \bm{p} = \frac{1-d}{N}\left(I-\alpha M\right)^{-1}\bm{1} \end{align}$$

で与えられます．

Pythonでの実装

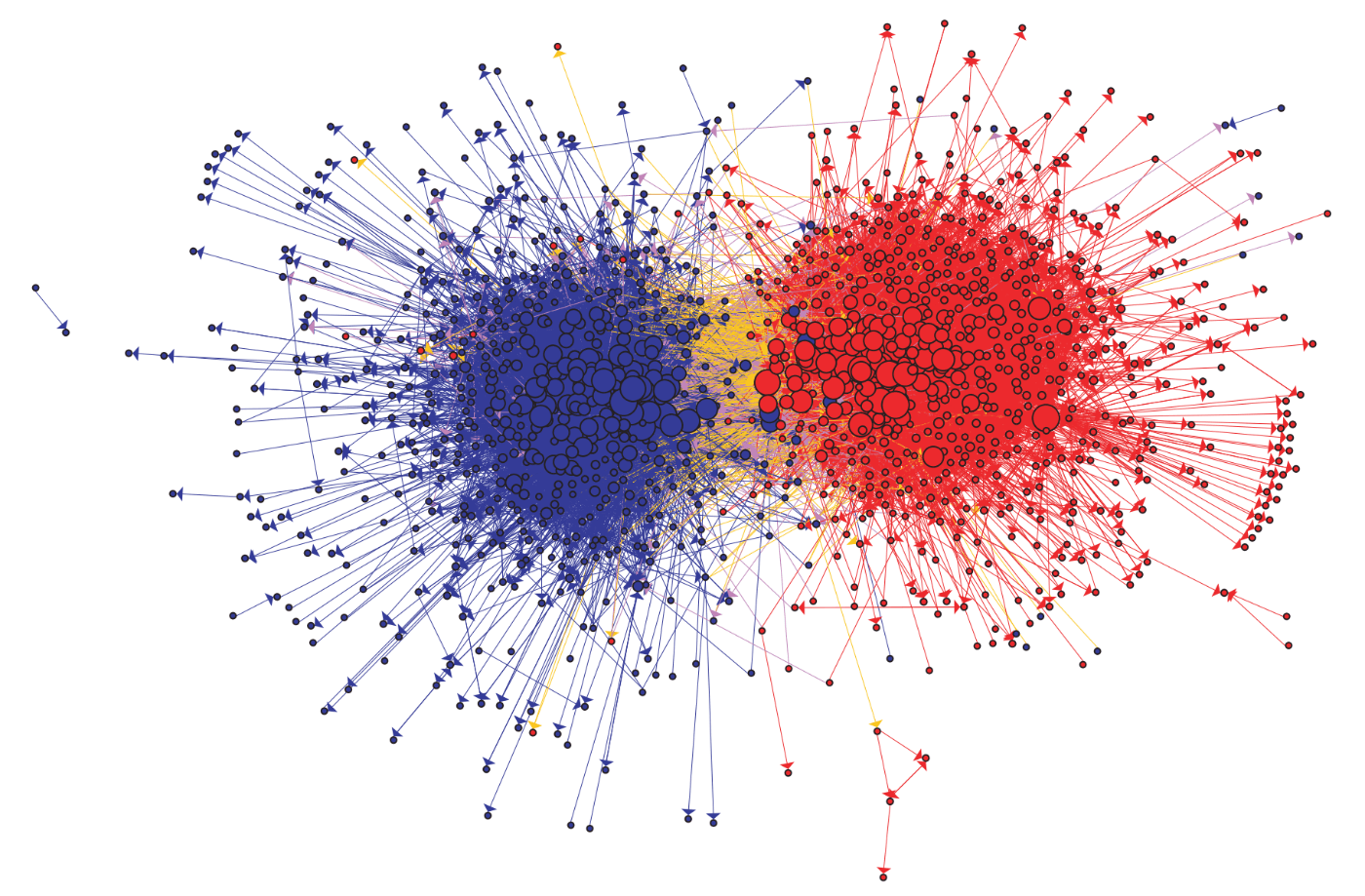
図1：Adamic and Glance (2005) が提示したアメリカの政治をテーマにしたブログの引用関係ネットワーク．赤色のノードは保守的なブログ，青色はリベラルなブログをそれぞれ表しており，リベラルから保守へのハイパーリンクは黄色で，保守からリベラルへのリンクは紫色で可視化されている．
出所）Adamic and Glance (2005)

PageRank を計算する PageRank() 関数を作り，図1で可視化されたアメリカの政治をテーマにしたブログの関係性を示す有向ネットワークの中心性を求めます^[2]．これまで実装した関数と違って，PageRank はオーソリティ中心性として定義されるので，隣接行列の転置を取ってから計算します．また，Brin and Page (1998) に合わせて，減衰係数はデフォルトで $d=0.85$ としておきます．

まず，引数に出次数の配列を受け取って各要素を $1$ と比較して大きい方を返す $\max(1,~k_i^{\text{out}})$ の処理を担う MAX() 関数を定義します．

def MAX(degree):
  """
  Returns the array of max(1, out-degree of i)
  """
  return np.array([i if i > 1 else 1 for i in degree])

MAX() 関数を使用して PageRank() 関数を定義します．ここでは $(9)$ 式を用いて実装しています．

def PageRank(A, alpha=0.85):
    """
    Computes the PageRank of A, defined as the x solving

    x = (1-alpha)/N1 + alpha A.T D x    (N = # nodes, 1 = vector of ones, D = diag(1 / max(1, out-degree)))

    Parameters
    ----------
    A : NumPy ndarray
        Adjacency matrix representation of graph.

    alpha : int or float (default: 0.85)
	Damping factor.

    Returns
    -------
    k : NumPy ndarray
        PageRank of A.

    """
    A_temp = A.T
    N = len(A_temp) # ノード数
    I = np.identity(N) # 単位行列

    out_degree = A @ np.ones(N) # 出次数ベクトル
    D = np.diag(1 / MAX(out_degree)) # 出次数の逆数を取った対角行列
    M = A_temp @ D # 行列Mを定義

    IA_inv = np.linalg.inv(I - alpha * M) # 逆行列
    return (1-alpha)*IA_inv @ np.ones(N) / N # (9)式

図1の有向ネットワークを graph-tool で生成し，まずは graph-tool で実装されている組み込み関数 graph_tool.centrality.pagerank() を使って中心性を計算し，中心性を反映する形で可視化します．

import graph_tool.all as gt
import matplotlib

g = gt.collection.data["polblogs"] # データの読み込み
g = gt.GraphView(g, vfilt=gt.label_largest_component(g)) # 孤立したネットワークを除去
pr = gt.pagerank(g) # graph-tool の組み込み関数で PageRank を計算
# ネットワークの可視化
gt.graph_draw(g, pos=g.vp["pos"], vertex_fill_color=pr,
               vertex_size=gt.prop_to_size(pr, mi=5, ma=15),
               vorder=pr, vcmap=matplotlib.cm.hot,
               vertex_shape="square");

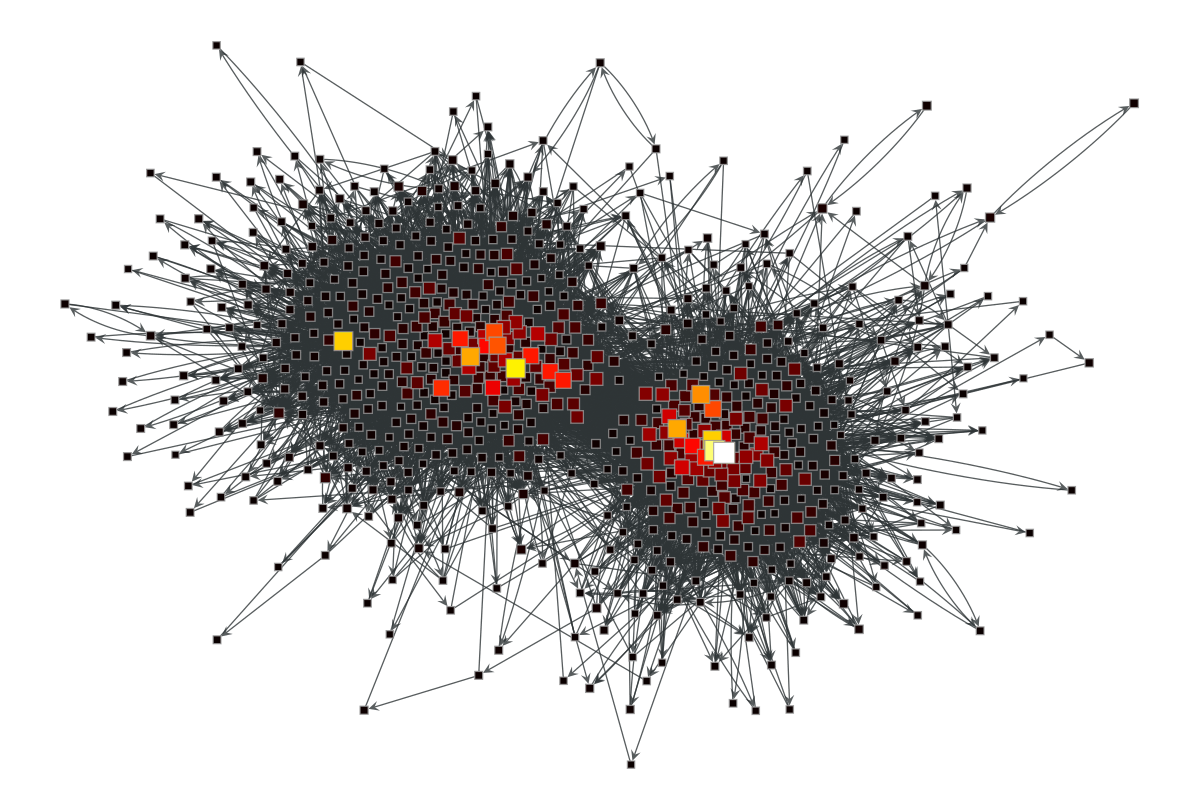
図2：graph-tool の関数で計算した PageRank．ノードの大きさは中心性の大きさに比例しており，明るいほど高い PageRank を持つ．

次に実装した PageRank() 関数を使って中心性を計算し，中心性を反映するようにネットワークを可視化します．今回は組み込み関数ではないため，可視化のために個々のノードの PageRank を VertexPropertyMap というノードの属性を管理するクラスに格納する必要があります．

## 自作の PageRank() で計算
# グラフを隣接行列に変換
A = gt.adjacency(g).toarray().T # graph-tool の隣接行列の定義は j --> i で a_{ij} = 1
pagerank = PageRank(A) # 自作関数で PageRank を計算

# PageRank を VertexPropertyMap に登録する
PR = g.new_vertex_property("double") 
for i, v in enumerate(g.vertices()):
    PR[v] = pagerank[i]

# ネットワークの可視化
gt.graph_draw(g, pos=g.vp["pos"], vertex_fill_color=PR,
               vertex_size=gt.prop_to_size(PR, mi=5, ma=15),
               vorder=PR, vcmap=matplotlib.cm.hot,
               vertex_shape="square");

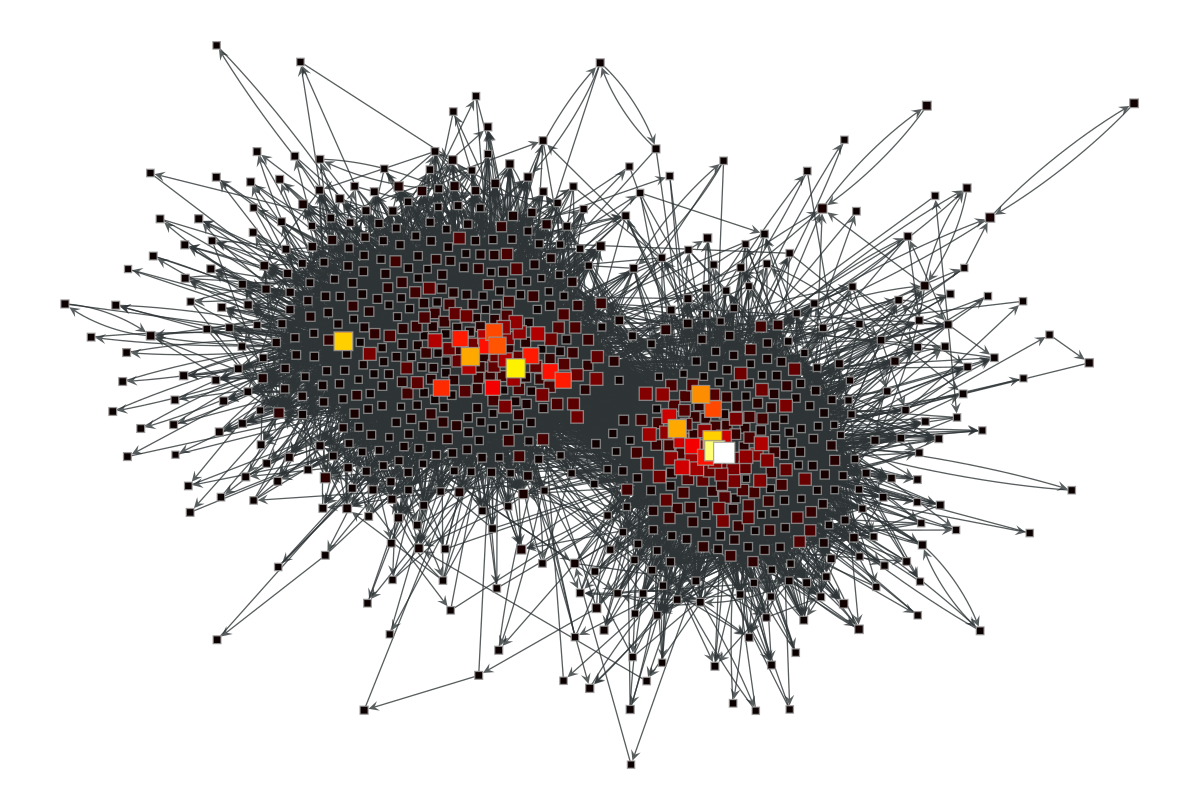
図3：実装した PageRank() 関数の計算結果．ノードの大きさは中心性の大きさに比例しており，明るいほど高い PageRank を持つ．

図2と図3を比べると，実装した PageRank() 関数でもしっかりランク付けできていることが確認できます．個々のノードの PageRank 同士を比べてみても，すべての値が近いことが確認できます．

## 要素同士の比較
gt_pagerank = np.array(list(pr)) # graph-tool の計算結果 pr を配列に変換

# 要素同士を参照して， PageRank() の浮動小数点演算の結果が graph-tool と近いか比較
np.allclose(gt_pagerank, pagerank) # >>> True

【おまけ】 PageRank とマルコフ連鎖

ここまで Katz 中心性の拡張として PageRank を定義し，さらに元論文 Brin and Page (1998) で導入されている減衰係数を加味した定義も確認しました．最後に，PageRank をマルコフ連鎖の定常分布というまた別の視点から眺めてみたいと思います．

本連載を企画した当初，マルコフ連鎖に言及する予定はなかったので，数学的な準備にあたる第2回と第3回ではマルコフ連鎖を一切扱っていません．マルコフ連鎖自体に馴染みのない方は，以下の記事を参照していただければと思います．

https://zenn.dev/kaityo256/articles/markov_eigenvalue#マルコフ行列
https://www.hello-statisticians.com/explain-terms-cat/markov_chain1.html

PageRank のエッセンスは，ノードのリンク元の出次数による相対的な重要性の変化に対処することにありました．ですので，ここでは $(2)$ 式を思い切り簡略化して

$$\begin{align} p_j = \alpha\sum_{i=1}^{n} a_{ij}\frac{p_i}{k_i^{\text{out}}} \end{align}$$

と定数項 $\beta$ を切り落としてしまいます．さらに，$\rho(A)<1$ が成り立っているとして $\alpha = 1$ とデフォルトの値を取るようにします．すると，$(10)$ 式は

$$\begin{align} p_j = \sum_{i=1}^{n} a_{ij}\frac{p_i}{k_i^{\text{out}}} \end{align}$$

となります．ノード $i$ のスコア $p_i$ を $i$ の出次数 $k_i^{\text{out}}$ で割り引くところが PageRank のエッセンスだったわけですが，隣接行列の要素 $a_{ij}$ を $k_i^{\text{out}}$ で割っても数式上問題はありません．すなわち，

$$\begin{align} p_j = \sum_{i=1}^{n}\frac{a_{ij}}{k_i^{\text{out}}}p_i \end{align}$$

と書けます．さらに，$(12)$ 式をベクトル形式で書くと，

$$\begin{align} \bm{p} = A^\top D^{-1}\bm{p} \end{align}$$

となります．ただし，$D=\text{diag}\left(k_i^{\text{out}}\right)$ です．さらに，$T \equiv D^{-1} A$ とおけば $(13)$ 式は

$$\begin{align} \bm{p} = T^\top\bm{p} \iff \bm{p}^\top T = \bm{p}^\top \end{align}$$

と書けます．つまり，ベクトル $\bm{p}$ は行列 $T$ の左固有ベクトルであることがわかります．

ところで， $T=(t_{ij})$ の $(i,j)$ 成分は隣接行列 $A$ の $(i,j)$ 成分をノード $i$ の出次数 $k_i^{\text{out}}$ で割った $a_{ij}/k_i^{\text{out}}$ になっています．したがって，$T$ の行和はどの行 $i$ についても必ず $1$ になっています．

$$\begin{align*} \forall i,~~~~\sum_{j=1}^nt_{ij}=\sum_{j=1}^n\frac{a_{ij}}{k_i^{\text{out}}} = \frac{\sum_{j=1}^na_{ij}}{k_i^{\text{out}}} = \frac{\sum_{j=1}^na_{ij}}{\sum_{j=1}^na_{ij}} = 1 \end{align*}$$

このように，任意の行和が $1$ になるような非負行列を推移行列 (transition matrix) といい，その$(i,j)$ 成分は状態 $i$ から状態 $j$ に推移する確率を表しています．今の文脈で言うと，推移行列 $T$ はランダムサーファーがハイパーリンクに沿ってページ $i$ から $j$ に遷移する確率を記述した行列であることになります．さらに，ページ $i$ の PageRank $p_i$ はランダムサーファーがページ $i$ に訪れる確率なので，これはサーファーがどのページにいるかを記述する状態確率ベクトル (state probability vector) であることになります．この推移行列と状態確率ベクトルで記述される次の状態が今の状態のみに依存する確率過程をマルコフ連鎖 (Markov chain) といいます．

PageRank $\bm{p}$ が $(14)$ 式のように推移行列 $T$ の固有値 $1$ に属する左固有ベクトルとして表せるということは，PageRank は推移行列 $T$ で表されるマルコフ連鎖の定常分布 (stationary distribution) に他ならないことを意味しています．直感的には，PageRankでは次のページへのリンクをランダムにクリックするネットサーファーが，無限回のクリックを経てたどり付く可能性の高いページほど重要であるということになります．PageRank はランダムサーフ（ランダムウォーク）の最終的な行き先の確率分布を表しているのです．

おわりに

本記事では，相手にとって自分が "one of them" なのか，それとも "only one" なのかを考慮した Katz 中心性の拡張としての PageRank を見た後，Brin and Page (1998) の減衰係数を導入した定義も紹介しました．その定義に基づいて Python で PageRank() を実装し，実際のネットワークデータを使って中心性指標として機能していることを確認しました．

本連載では，次数中心性を拡張していく形で固有ベクトル中心性や Katz 中心性を紹介してきたため，この記事でも同様に PageRank を次数中心性の拡張の流れの中で紹介しました．しかし，PageRank は元論文 Brin and Page (1998) においては，ネットワーク上のランダムウォークとして導入されているので，最後に PageRank はランダムウォークの定常分布というもう一つの顔を持つことを説明しました．

最後に，Newman (2018) に倣って，今まで取り上げてきた中心性指標を表にまとめておきます．どの中心性も隣接行列に基づいて計算されますが，定数項があるかどうか，出次数で割り引くかどうかで区別できます．

	定数項あり	定数項なし
出次数で割り引く	PageRank	次数中心性
割り引かない	Katz 中心性	固有ベクトル中心性

参考文献

• Adamic, L. A., & Glance, N. (2005, August). The political blogosphere and the 2004 US election: divided they blog. In Proceedings of the 3rd international workshop on Link discovery (pp. 36-43).
• Brin, S., & Page, L. (1998). The anatomy of a large-scale hypertextual web search engine. Computer networks and ISDN systems, 30(1-7), 107-117.
• John Stachurski and Thomas J. Sargent. Economic Networks: Theory and Computation (QuantEcon, 2022). URL https://networks.quantecon.org/ .
• Newman, M. (2018). Networks. Oxford university press.

脚注

1. 元論文 Brin and Page (1998) では，PageRank はグラフ上のランダムウォークとして導入されていますが，本連載はまず Katz 中心性を拡張する形で議論を進めていきます．

2. Adamic and Glance (2005) は，2004年のアメリカ大統領選挙に先立つ2ヶ月の間に投稿されたブログを分析し，リベラルと保守の両コミュニティ内外のブログの参照関係を明らかにしました．彼らによるとリベラルと保守の振る舞いには違いが見られ，リベラルなブログは保守のブログも参照するのに対して，保守のブログの方がより頻繁に，保守同士で参照し合う傾向があったということです．ネットワークの構造に政治的な分断が反映されているのは興味深いですね