シリーズの目次
- Introduction
- 線形代数
- グラフ理論
- 次数中心性
- 固有ベクトル中心性
- Katz 中心性
- PageRank
ネットワークと行列
いきなり線形代数の話をする前に,どうしてネットワークの中心性を考えるのに線形代数が必要かを簡単に説明します.当たり前のことですが,あるノードの中心性を計算するには,そのノードを含むネットワークの情報が必要になります.たとえば,ノード i さんに「あなたは何人の友達を持っていますか?(何個のノードと繋がっていますか?)」と聞いてみましょう.ノード i さんは,「私の友達は j さんと k さんと...さんなので,全部で〇〇人です!」と答えるでしょう.
この時 i さんは自分が誰と繋がっているかという情報を使っています.この誰が誰と繋がっているかを簡単に表現できる良い方法があれば良いですよね.ここで登場するのが行列です.行列 A=(a_{ij}) を用意して, i さんと j さんが繋がっていれば a_{ij}=1,そうでなければ a_{ij}=0 とすれば,ネットワーク上で誰と誰が繋がっているかを完璧に表現できます.
中心性を計算する際にネットワークの情報を使うということは,ネットワークを表現する行列 A の情報を使用するということです.ですから,必然的に線形代数の力が発揮されるわけです.また,そもそもネットワークが行列で表現されることは,行列の持つ性質がネットワークの性質を決定してることを意味します.ですから,ネットワークのことを考える上で,行列の持つ性質を考える線形代数の知識は自ずと必要になります.この点については,次回のグラフ理論の記事で取り上げます.
中心性計算に必要な線形代数の知識
この記事では,線形代数の中でも中心性を計算するタスクに必要なものを取り上げます.
- 固有値・固有ベクトル
- 対角化と行列のべき乗
- ノイマン級数の補題
- ペロン=フロベニウスの定理
固有値・固有ベクトル
n 次正方行列 A\in\mathbb{M}^{n \times n} に対して,
を満たす非ゼロベクトル \bm{v} \in \mathbb{C}^n が存在する時,スカラー \lambda \in \mathbb{C} を A の固有値 (eigenvalue),\bm{v} を A の固有ベクトル (eigenvector) と呼びます.一般に,ベクトルに行列を作用させると,方向と大きさが変わります.しかし,固有ベクトルについては,行列を作用させてもベクトルの方向は保存され,その大きさだけが変わる(\lambda 倍)ということです.A の全ての固有値からなる集合を A のスペクトル (spectrum) といい,\sigma(A) と表記します.A は最大で n 個の固有値を持ちます.
例
以下で与えられる行列 A のスペクトルと,それに対応する固有ベクトルを求めよ.
A = \begin{pmatrix} 0 & -1 \\ 1 & 0
\end{pmatrix}
\begin{align*}
\left|A - \lambda I\right| =
\begin{vmatrix}
-\lambda & -1 \\
1 & -\lambda
\end{vmatrix}
= \lambda^2 + 1
= 0
\end{align*}
より \lambda \pm i.c を非ゼロの任意定数とする.
\lambda = i のとき
\begin{align*}
\begin{pmatrix}
-i & -1 \\
1 & -i
\end{pmatrix}
\begin{pmatrix}
v_1 \\
v_2
\end{pmatrix} =
\begin{pmatrix}
0 \\
0
\end{pmatrix}
&\iff v_1 - iv_2 = 0 \\
&\iff
\begin{cases}
v_1 = -c \\
v_2 = ic
\end{cases} \\
\therefore~~\bm{v} = c
\begin{pmatrix}
-1 \\
i
\end{pmatrix}
\end{align*}
\lambda = -i のとき
\begin{align*}
\begin{pmatrix}
i & -1 \\
1 & i
\end{pmatrix}
\begin{pmatrix}
v_1 \\
v_2
\end{pmatrix} =
\begin{pmatrix}
0 \\
0
\end{pmatrix}
&\iff v_1 + iv_2 = 0 \\
&\iff
\begin{cases}
v_1 = -c \\
v_2 = -ic
\end{cases} \\
\therefore~~\bm{v} = c
\begin{pmatrix}
-1 \\
-i
\end{pmatrix}
\end{align*}
以上より,\sigma(A) = \{i, -i\} で,対応する固有ベクトルはそれぞれ
\begin{pmatrix}
-1 \\
i
\end{pmatrix},~
\begin{pmatrix}
-1 \\
-i
\end{pmatrix}
である.
\lambda \in \sigma(A) において,\bm{v} が固有値 \lambda に属する固有ベクトルであるとき,(\lambda, \bm{v})は固有対 (eigenpair) と呼ばれます.ベクトルに非ゼロのスカラー \alpha をかけた場合の (\lambda, \alpha\bm{v}) もまた,A の固有対となります.
証明
(\lambda, \bm{v}) が A の固有対であるので,A\bm{v} = \lambda\bm{v}.両辺を \alpha 倍すると,\alpha(A\bm{v}) = \alpha(\lambda\bm{v}).これを変形するとA(\alpha\bm{v}) = \lambda(\alpha\bm{v}) となり,\alpha\bm{v} は固有値 \lambda に属する固有ベクトルである.よって,(\lambda, \alpha\bm{v}) は A の固有対である.
\lambda \in \mathbb{C} が A の固有値であることと,\det{(A-\lambda I)} = 0 であることは同値です.
証明
A\bm{v} = \lambda\bm{v} より (A-\lambda I)\bm{v} = \bm{0}.\det{(A-\lambda I)} \neq 0 を仮定すると (A-\lambda I) は逆行列 (A-\lambda I)^{-1} を持つ.この時 \bm{v} = (A-\lambda I)^{-1}\bm{0} = \bm{0} となり,\bm{v} が固有ベクトルであることに反する.よって,\det{(A-\lambda I)} = 0.
ここで出てきた p(\lambda) \coloneqq \det{(A-\lambda I)} は,n 次多項式です.p(\lambda) は A の固有多項式と呼ばれ,代数学の基本定理より 固有方程式 p(\lambda) = 0 を複素数の範囲で解けば、重複度を含めて n 個の根 (root) が求まります.p(\lambda) の因数分解において,\lambda \in \sigma(A) が k 回現れるとき,\lambda は k の代数的重複度を持つといいます.重複度 k = 1 の固有値 \lambda を単根 (simple root) と呼び,単根の固有値 \lambda はスカラー倍の差を除いて一意の固有ベクトルを持つという性質があります.
固有方程式 p(\lambda) = 0 が n 個の相異なる固有値を持つとき,固有値に属するn 個の固有ベクトルは複素 n 次元空間 \Complex^n の基底を成します.
証明
固有方程式 \det{(A-\lambda I)} = 0 が n 個の相異なる固有値を持つとき,|\sigma(A)| = n となる.固有値 \lambda_i \in \sigma(A) に属する固有ベクトルを \bm{v}_i とする.\{\bm{v}_i\}_{i=1}^n が複素 n 次元空間 \Complex^n の基底を成すことを示すには,\{\bm{v}_i\}_{i=1}^n が線形独立であることを示せば良い.
n=1 のとき成立は明らか.n=k のとき \{\bm{v}_i\}_{i=1}^k が線形独立であることを仮定する.c_i を任意定数として
\begin{align}
\sum_{i=1}^{k+1} c_i\bm{v}_i = \bm{0}
\end{align}
を考える.両辺に左から A をかけると
\begin{align}
A\left(\sum_{i=1}^{k+1} c_i\bm{v}_i\right) = \sum_{i=1}^{k+1} c_i A\bm{v}_i = \sum_{i=1}^{k+1} c_i \lambda_i\bm{v}_i = \bm{0}
\end{align}
(1) の両辺に \lambda_{k+1} をかけて,
\begin{align}
\lambda_{k+1}\left(\sum_{i=1}^{k+1} c_i\bm{v}_i\right) = \sum_{i=1}^{k+1} c_i \lambda_{k+1}\bm{v}_i = \bm{0}
\end{align}
(2) と (3) の辺々を引くと
\sum_{i=1}^{k} c_i\left(\lambda_i - \lambda_{k+1}\right)\bm{v}_i = \bm{0}
\{\bm{v}_i\}_{i=1}^k は線形独立なので
c_i\left(\lambda_i - \lambda_{k+1}\right) = 0~~~~\forall i = 1,\dots,k
\lambda_i - \lambda_{k+1} \neq 0 より c_i = 0~~\forall i = 1,\dots,k.これを (1) に代入して,c_{k+1}\bm{v}_{k+1} = \bm{0} となるが,\bm{v}_{k+1} \neq \bm{0} より c_{k+1} = 0.よって,\{\bm{v}_i\}_{i=1}^{k+1} は線形独立である.数学的帰納法から\{\bm{v}_i\}_{i=1}^n は線形独立である.
先ほど,ベクトルをスカラー倍した時の固有値を考えました.ところで,行列をスカラー倍すると固有値はどうなるのでしょうか.行列 A \in \mathbb{M}^{n \times n} については次の関係が成り立ちます.
\lambda \in \sigma(A) \iff \forall \tau \gt 0,~\tau\lambda \in \sigma(\tau A)
証明
(\implies) \lambda \in \sigma(A) より \lambda に属する固有ベクトル \bm{v}\in\Complex^n が存在して,A\bm{v} = \lambda\bm{v} である.両辺に \tau(\gt0) をかけて \tau(A\bm{v}) = \tau(\lambda\bm{v}).すなわち (\tau A)\bm{v} = (\tau\lambda)\bm{v} であり,\tau\lambda は 行列 \tau A の固有値である.よって,\tau\lambda \in \sigma(\tau A).
(\impliedby) \tau\lambda \in \sigma(\tau A) において,\lambda' = \tau\lambda とおくと \lambda' \in \sigma(\tau A). 任意の \tau (\gt 0) について \tau^{-1}\lambda' \in \sigma(\tau^{-1}\tau A) が成り立つ.よって,\lambda \in \sigma(A).
左右の固有ベクトル
行列 A\in\mathbb{M}^{n \times n} に対して
で定義された固有ベクトル \bm{v}を右固有ベクトル (right eigenvector) と呼ぶことがあります.以後右固有ベクトルを \bm{e} で表します.すなわち,
が成り立ちます.右があるなら左もあるということで,行列 A\in\mathbb{M}^{n \times n} に対して
A^\top\bm{\varepsilon} = \lambda\bm{\varepsilon}
を満たす非ゼロベクトル \bm{\varepsilon} \in \Complex^n が存在する時,\bm{\varepsilon} を A の左固有ベクトル (left eigenvector) と呼びます.どうして左と冠するかというと,転置をとると
\bm{\varepsilon}^\top A = \lambda\bm{\varepsilon}^\top
とも書けるからです.
対角化
「正方行列の中で最も扱いやすい行列は何か?」と聞かれれば,多くの人は対角行列と答えるでしょう.対角行列には次のような性質があるからです. D = \text{diag}(\lambda_i),~i = 1,\dots,n とすると
- 行列のべき乗の計算が楽: D^m = \text{diag}(\lambda_i^m)
- 逆行列が一瞬で求まる: \forall i, \lambda_i \gt 0 \implies D^{-1} = \text{diag}(\lambda_i^{-1})
- 1次連立方程式 D\bm{x} = \bm{b} は,n 本の完全に独立した方程式になる.すなわち
\begin{pmatrix}
\lambda_1 & & \text{\LARGE{0}} \\
& \ddots & \\
\text{\LARGE{0}} & & \lambda_n
\end{pmatrix}
\begin{pmatrix}
x_1 \\
\vdots \\
x_n
\end{pmatrix} =
\begin{pmatrix}
b_1 \\
\vdots \\
b_n
\end{pmatrix}
\iff \lambda_ix_i = b_i~~~~\forall i = 1,\dots,n
特に一番目の性質が多くの場面で役に立ちます.ある行列 A のべき乗 A^m が欲しい時,それを直接計算して求めるのはかなり面倒です.しかし,対角行列のべき乗は計算が比較的容易であることを考えると,A を何らかの形で対角行列として捉えることができれば良さそうです.それが行列の対角化という操作になります.
行列 A\in\mathbb{M}^{n \times n} は次の条件を満たすとき対角化可能 (diagonalizable) であるといいます:
\exists~D = \text{diag}(\lambda_1,\dots,\lambda_n),~P\in\mathbb{M}^{n \times n}~\text{s.t.}~ A = PDP^{-1}.
ただし,P は正則行列です.A = PDP^{-1} という表現を A の固有値分解 (eigendecomposition) といいます.
対角化を写像の観点で眺めると,次のようになっています.
\begin{CD}
\R^n @>A>> \R^n \\
@VP^{-1}VV @AAPA \\
\Complex^n @>D>> \Complex^n
\end{CD}
つまり,行列 A で直接 A:\R^n \to \R^n の線形写像を行う代わりに,
-
P^{-1} で一度複素空間 \Complex^n に移動し,
-
D を作用させ,
-
P で再び \R^n に戻る
という3つのステップを踏んでいるわけです.たとえばベクトル \bm{x} に行列 A を作用させる操作を考えます.
より,ステップ1で P = (\bm{p}_i,\dots,\bm{p}_n) の列ベクトルを基底とした時の \bm{x} = \sum_i x_i \bm{p}_i の各 \bm{p}_i 方向の成分 x_i を抽出し,ステップ2で対角行列 D によって各成分 x_i を固有値倍(\lambda_ix_i)し,ステップ3で基底 \{\bm{p}_i\}_{i=1}^n と成分 \lambda_ix_i を使ってベクトルに戻すという操作をしていることがわかります.
例
先ほど固有値・固有ベクトルの例として,行列 A を考えました.
A = \begin{pmatrix} 0 & -1 \\ 1 & 0
\end{pmatrix}
これは任意の2次元ベクトル \bm{x}\in\R^2 を,原点を中心に左に 90\degree 回転させる回転行列です.ですので,たとえば \bm{x} = (4,0)^\top とすると, A\bm{x} = (0,4)^\top と回転されます.ここでは行列 A を固有値分解した行列 PDP^{-1} でも \bm{x} が (0,4)^\top に変換されるかをステップ1からステップ3を具体的に追いながら確認します.
まず,\sigma(A) = \{i, -i\} で,対応する固有ベクトルはそれぞれ
\begin{pmatrix}
-1 \\
i
\end{pmatrix},~
\begin{pmatrix}
-1 \\
-i
\end{pmatrix}
ですので,A を対角化すると
A = PDP^{-1} =
\begin{pmatrix}
-1 & -1 \\
i & -i
\end{pmatrix}
\begin{pmatrix}
i & 0 \\
0 & -i
\end{pmatrix}
\begin{pmatrix}
-0.5 & -0.5i \\
-0.5 & 0.5i
\end{pmatrix}
となります.
ステップ1
\begin{align*}
PDP^{-1}\bm{x} &=
\begin{pmatrix}
-1 & -1 \\
i & -i
\end{pmatrix}
\begin{pmatrix}
i & 0 \\
0 & -i
\end{pmatrix}
\begin{pmatrix}
-0.5 & -0.5i \\
-0.5 & 0.5i
\end{pmatrix}
\begin{pmatrix}
4 \\
0
\end{pmatrix} \\ &=
\begin{pmatrix}
-1 & -1 \\
i & -i
\end{pmatrix}
\begin{pmatrix}
i & 0 \\
0 & -i
\end{pmatrix}
\begin{pmatrix}
-2 \\
-2
\end{pmatrix}
\end{align*}
右端の列ベクトル (-2,-2)^\top には,P^{-1} で抽出された P の列ベクトルの組 \{\bm{p}_1,\bm{p}_2\} を基底とした時の \bm{x} の各成分 x_i が並んでいます.実際,
\bm{x} = x_1\bm{p}_1 + x_2\bm{p}_2 = -2
\begin{pmatrix}
-1 \\
i
\end{pmatrix}-2
\begin{pmatrix}
-1 \\
-i
\end{pmatrix}
であることから確認できます.
ステップ2
\begin{align*}
PDP^{-1}\bm{x} &=
\begin{pmatrix}
-1 & -1 \\
i & -i
\end{pmatrix}
\begin{pmatrix}
i & 0 \\
0 & -i
\end{pmatrix}
\begin{pmatrix}
-2 \\
-2
\end{pmatrix} \\ &=
\begin{pmatrix}
-1 & -1 \\
i & -i
\end{pmatrix}
\begin{pmatrix}
-2i \\
2i
\end{pmatrix}
\end{align*}
対角行列 D = \text{diag}(i,-i) によって各成分 x_i を固有値倍(\lambda_ix_i)しています.
ステップ3
\begin{align*}
PDP^{-1}\bm{x} &=
\begin{pmatrix}
-1 & -1 \\
i & -i
\end{pmatrix}
\begin{pmatrix}
-2i \\
2i
\end{pmatrix} \\ &=
-2i
\begin{pmatrix}
-1 \\
i
\end{pmatrix}
+ 2i
\begin{pmatrix}
-1 \\
-i
\end{pmatrix} \\ &=
\begin{pmatrix}
0 \\
4
\end{pmatrix}
\end{align*}
基底 \{\bm{p}_1,\bm{p}_2\} と成分 (-2i,2i)^\top を使ってベクトルを生成すると,(0,4)^\top になり,A\bm{x} = (0,4)^\top と一致することが確認できます.
このあたりはデータサイエンスVTuberアイシア=ソリッドさんがわかりやすく解説してくださっているので視聴をおすすめします.
https://youtu.be/YVIMrAzAG5s?si=AS7O0p566j470i7T
行列のべき乗
行列が対角化できると,次のような方法を使って行列のべき乗の計算を楽に行えます.
A = PDP^{-1} = P\text{diag}(\lambda_i)P^{-1} \implies A^m = P\text{diag}(\lambda_i^m)P^{-1}~~\forall~m \in \N.
証明
m=1 のときは明らか.m=k のとき成立を仮定すると,A^k = P\text{diag}(\lambda_i^k)P^{-1}となる.A^{k+1} を考える.
\begin{align*}
A^{k+1} &= AA^k \\
&= AP\text{diag}(\lambda_i^k)P^{-1} \\
&= P\text{diag}(\lambda_i)P^{-1}P\text{diag}(\lambda_i^k)P^{-1} \\
&= P\text{diag}(\lambda_i^{k+1})P^{-1}
\end{align*}
数学的帰納法より成立.
つまり,A^m を計算するには,対角行列 D の各成分(固有値 \lambda_i)を m 乗した後で,左から P を右から P^{-1}をかければ良いことになります.
対角化によって行列のべき乗の計算が楽になることを確認しました.では,どのような場合に行列を対角化できるのでしょうか.行列 A\in\mathbb{M}^n は,その固有ベクトル \{\bm{p}_i\}_{i=1}^n が \Complex^n の基底を成す時かつその時に限って対角化可能です.
証明
(\implies) A が対角化可能であるとすると, A = PDP^{-1} である.このとき P は正則でなければならず,したがって P の n 個の列ベクトル \{\bm{p}_i\}_{i=1}^n は線形独立であり,\Complex^n の基底を形成する.
(\impliedby) A の固有ベクトル \{\bm{p}_i\}_{i=1}^n が \Complex^n の基底を成すとすると,\{\bm{p}_i\}_{i=1}^nは線形独立である.固有ベクトルの定義より A\bm{p}_i = \lambda_i\bm{p}_i である.\{\bm{p}_i\}_{i=1}^nが線形独立なので,正則な行列 P = \left(\bm{p}_1,\dots,\bm{p}_n\right) を作ることができる.D = \text{diag}(\lambda_i) とすると
\begin{align*}
\left(A\bm{p}_1,\dots,A\bm{p}_n\right) = \left(\lambda_1\bm{p}_1,\dots,\lambda_n\bm{p}_n\right)
&\iff A\left(\bm{p}_1,\dots,\bm{p}_n\right) = \left(\bm{p}_1,\dots,\bm{p}_n\right)
\begin{pmatrix}
\lambda_1 & & \text{\LARGE{0}} \\
& \ddots & \\
\text{\LARGE{0}} & & \lambda_n
\end{pmatrix} \\
&\iff AP = PD \\
&\iff A = PDP^{-1}
\end{align*}
対角化と左右の固有ベクトル
対角化と左右の固有ベクトルの関係を見てみます.同じ行列に対して右固有ベクトルと左固有ベクトルが定義できたので,行列の対角化にも何らかの形で関わっていそうです.
まず,A が対角化可能であるとき,A^\top も対角化可能であることを確かめます.Q = (P^\top)^{-1} とします.一般に,正方行列 A について
\left(A^\top\right)^{-1} = \left(A^{-1}\right)^\top
が成り立つので,
A^\top = \left(PDP^{-1}\right)^\top = \left(P^{-1}\right)^\top\left(PD\right)^\top =\left(P^\top\right)^{-1}D^\top P^\top = QDQ^{-1}.
よって,A が対角化可能であるとき A^\top は正則行列 Q で対角化できます.
ここで,行列 A の右固有ベクトルを\{\bm{e}_i\}_{i=1}^n,左固有ベクトルを\{\bm{\varepsilon}_i\}_{i=1}^nとして,正則行列 P と P^{-1} をそれぞれ次のように表記します.
P = \left(\bm{e}_1,\dots,\bm{e}_n\right),~~
P^{-1} =
\begin{pmatrix}
\bm{\varepsilon}_1^\top \\
\vdots \\
\bm{\varepsilon}_n^\top
\end{pmatrix}
A = PDP^{-1} に対して,右から P をかけると
\begin{align*}
AP = PD &\iff
A\left(\bm{e}_1,\dots,\bm{e}_n\right) = \left(\bm{e}_1,\dots,\bm{e}_n\right)
\begin{pmatrix}
\lambda_1 & & \text{\LARGE{0}} \\
& \ddots & \\
\text{\LARGE{0}} & & \lambda_n
\end{pmatrix} \\
&\iff
\left(A\bm{e}_1,\dots,A\bm{e}_n\right) = \left(\lambda_1\bm{e}_1,\dots,\lambda_n\bm{e}_n\right).
\end{align*}
また,A = PDP^{-1} に対して,左から P^{-1} をかけると
\begin{align*}
P^{-1}A = DP^{-1} &\iff
\begin{pmatrix}
\bm{\varepsilon}_1^\top \\
\vdots \\
\bm{\varepsilon}_n^\top
\end{pmatrix} A =
\begin{pmatrix}
\lambda_1 & & \text{\LARGE{0}} \\
& \ddots & \\
\text{\LARGE{0}} & & \lambda_n
\end{pmatrix}
\begin{pmatrix}
\bm{\varepsilon}_1^\top \\
\vdots \\
\bm{\varepsilon}_n^\top
\end{pmatrix} \\
&\iff
\begin{pmatrix}
\bm{\varepsilon}_1^\top A \\
\vdots \\
\bm{\varepsilon}_n^\top A
\end{pmatrix} =
\begin{pmatrix}
\lambda_1\bm{\varepsilon}_1^\top \\
\vdots \\
\lambda_n\bm{\varepsilon}_n^\top
\end{pmatrix}
\end{align*}
つまり,任意の i = 1,\dots,n について A\bm{e}_i = \lambda_i\bm{e}_i と \bm{\varepsilon}_i^\top A = \lambda_i\bm{\varepsilon}_i^\top が成り立ちます.この事実から,行列の対角化 A = PDP^{-1} について次のことがわかります.
- 正則行列 P は A の右固有ベクトル \bm{e}_i を横に並べたもの
- 正則行列 P^{-1} は A の左固有ベクトルを転置した \bm{\varepsilon}_i^\top を縦に並べたもの
-
A の右固有ベクトル \bm{e}_i と左固有ベクトル\bm{\varepsilon}_i は固有値 \lambda_i を共有する
- よって, A と A^\top のスペクトルは等しい:\sigma(A) = \sigma(A^\top)
ノイマン級数の補題
実数 r(|r|<1) に対しては,無限等比級数の和の公式があり,
\sum_{n=0}^\infty r^n = \frac{1}{1-r}
であることが知られています.この等比級数 (geometric series) の公式を行列に拡張したものがノイマン級数 (Neumann series) です.すなわち,ある条件を満たす正方行列 A に対しては
\sum_{m=0}^\infty A^m = I + A + A^2 + \cdots = \left(I - A\right)^{-1}
が成り立ちます.これを成立させる条件は,実数における |r|<1 という条件を行列に一般化したものであり,それは行列 A のスペクトル半径で表されます.
スペクトル半径
行列 A\in\mathbb{M}^{n \times n} のスペクトル半径 (spectral radius) \rho(A) は,固有値の絶対値の最大値として定義されます.すなわち,z \in \Complex に対して |z| を絶対値とすると,
\rho(A) \coloneqq \max\left(|\lambda|:~\lambda \in \sigma(A)\right).
スペクトル半径を使えば,行列のべき乗の極限における振る舞いを議論できます.行列 A が A = PDP^{-1} と対角化されるなら,
A^m = P
\begin{pmatrix}
\lambda_1^m & & \text{\LARGE{0}} \\
& \ddots & \\
\text{\LARGE{0}} & & \lambda_n^m
\end{pmatrix} P^{-1}
なので,m \to \infty で A^m が発散するか収束するかは,\rho(A) が決定します.\rho(A) > 1 のとき m \to \infty で \lambda_i^m \to \infty となる i が存在するので,A^m は発散します.逆に \rho(A) < 1 ならば A^m \to O が成り立ちます.
ノイマン級数の補題
導入部分で「ある条件」としていた部分を明記して,ノイマン級数の補題 (Neumann series lemma) の主張を見てみましょう.
正方行列 A \in \mathbb{M}^{n \times n} について, \rho(A) < 1 であるとき I - A は正則であり,
\left(I - A\right)^{-1} = \sum_{m=0}^\infty A^m
が成立します.行列の級数の収束は,各要素の収束によって定義されます.
応用例:線形システム
次の線形システム (linear system) を考えます. A は n \times n 行列です.
\bm{x} = A\bm{x} + \bm{b}
このシステムは \rho(A) < 1 ならば,任意の \bm{b} \in \R^n に対して一意の解 \bm{x}^* を持ち,それは
\bm{x}^* = \sum_{m=0}^\infty A^m \bm{b}
で与えられます.
証明
\rho(A) < 1 より I -A は正則で逆行列が存在し,(I-A)^{-1} = \sum_{m=0}^\infty A^m である.\bm{x} = A\bm{x} + \bm{b} より (I-A)\bm{x} = \bm{b} であるから
\bm{x} = (I-A)^{-1}\bm{b} = \sum_{m=0}^\infty A^m \bm{b}
ペロン=フロベニウスの定理
ペロン=フロベニウスの定理 (Perron–Frobenius Theorem) は,行列が何らかの意味で"正"であるときに,その固有値と固有ベクトルについて何が言えるかを述べた強力な定理です.確率論,数値解析,経済学など,さまざまな分野で応用されています.
行列の分類
成分がすべて非負であるような行列を非負行列 (nonnegative matrix),すべて正であるような行列を正行列 (positive matrix) といいます.次の例では A は非負行列,B は正行列です.
A =
\begin{pmatrix}
0 & 1 \\
2 & 3
\end{pmatrix}, ~
B =
\begin{pmatrix}
1 & 2 \\
3 & 4
\end{pmatrix}
ここでは非負行列 A = (a_{ij}) \in \mathbb{M}^{n \times n} と正行列 B = (b_{ij}) \in \mathbb{M}^{n \times n} を次のように表記します.
\begin{align*}
A \geqslant O &\iff a_{ij} \geqslant 0~~\forall i,j \\
B \gg O &\iff b_{ij} > 0~~\forall i,j
\end{align*}
非負行列 A \geqslant O について,
-
\sum_{m=0}^\infty A^m \gg O が成り立つとき,A は既約 (irreducible) であるといい,
-
A^m \gg O となるような m \in \N が存在するとき,A は原始的 (primitive) である
といいます.原始性は既約性よりも強い条件です.ここで挙げた行列の分類の関係は次のようになっています.
A \gg O \implies A \text{ primitive} \implies A \text{ irreducible} \implies A \geqslant O
定理の内容
一般に, n \times n 行列 A においてスペクトル半径 \rho(A) は固有値ではありません.たとえば,D = \text{diag}(-1 , 0) のスペクトル半径は \rho(D) = 1 ですが,スペクトルは \sigma(D) = \{-1 , 0\} なので,固有値と一致しません.
しかし,非負行列であればスペクトル半径と固有値が一致することがペロン=フロベニウスの定理から保証されます.定理の主張は以下の通りです.
A \geqslant O であるとき,A のスペクトル半径 \rho(A) は A の固有値であり,\rho(A) に属する右・左固有ベクトルは非負の実数からなる.つまり,
\exists~\bm{e},\bm{\varepsilon} \in \R_{+}~\text{s.t.}~A\bm{e}=\rho(A)\bm{e},~\bm{\varepsilon}^\top A=\rho(A)\bm{\varepsilon}^\top.
加えて,A が既約ならば
-
\rho(A) > 0 は単根の固有値(単純固有値)
- 右固有ベクトル \bm{e} も左固有ベクトル \bm{\varepsilon} も,その成分はすべて正
-
\rho(A) 以外の固有値に属する固有ベクトルは非負にならない
さらに,A が原始的ならば
-
\rho(A) 以外のすべての固有値 \lambda について |\lambda| \leqslant \rho(A)
-
\left< \bm{\varepsilon}, \bm{e} \right> = 1 と基準化すると
\left[\frac{A}{\rho(A)}\right]^m \to ~\bm{e}\bm{\varepsilon}^\top~~~~(m \to \infty)
この\rho(A) は A のペロン=フロベニウス固有値 (Perron–Frobenius eigenvalue) または支配的な固有値 (dominant eigenvalue) と呼ばれ,\rho(A) に属する右・左固有ベクトルも支配的な右(左)固有ベクトル (dominant left/right eigenvector) と呼ばれます.
支配的な固有ベクトルの意味
ペロン=フロベニウス固有値に属する固有ベクトルが,「支配的」であるとはどういうことでしょうか.原始的な行列 A \in \mathbb{M}^{n \times n} と任意の非ゼロベクトル \bm{x} \in \R^n を考えます.\bm{x} を A で m 回変換すると,十分大きな m について
\begin{align*}
A^m\bm{x} &\approx \rho(A)^m\bm{e}\bm{\varepsilon}^\top\bm{x} \\
&= c\rho(A)^m\bm{e} ~~~~(c=\bm{\varepsilon}^\top\bm{x})
\end{align*}
つまり,ベクトルを A で繰り返し変換していくと,右固有ベクトル \bm{e} のスカラー倍(c\rho(A)^m 倍)に漸近していくということです.繰り返し変換することでどんなベクトルも最終的に \bm{e} と同じ方向に揃うことから,\bm{e} を支配的な固有ベクトルと考えることができるわけです.
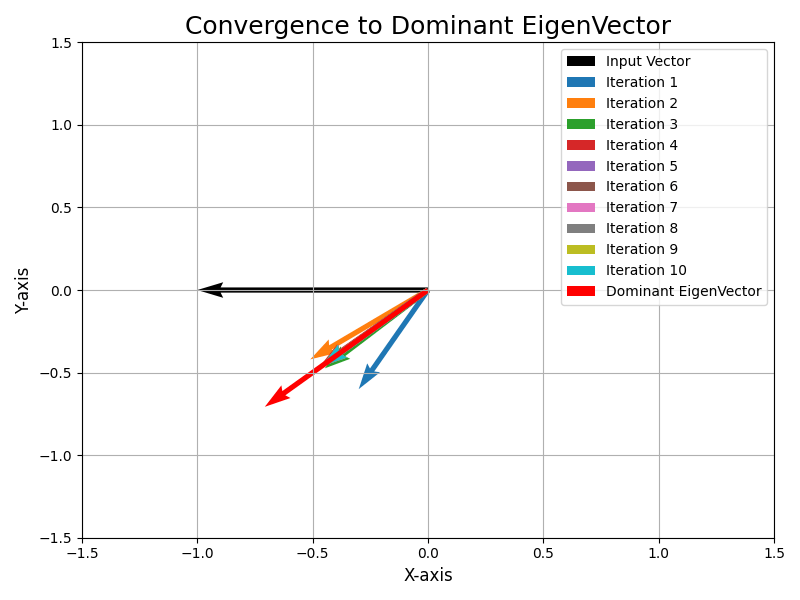
上図は
A =
\begin{pmatrix}
0.3 & 0.7 \\
0.6 & 0.4
\end{pmatrix},~~\bm{x} =
\begin{pmatrix}
-1 \\
0
\end{pmatrix}
として,Aで \bm{x} を繰り返し変換させた様子です.黒色の矢印が \bm{x} で,赤色の矢印が支配的な固有ベクトルです.3回目の変換という早い段階で, \bm{x} が支配的な固有ベクトルに収束していることがわかります.
Code
import numpy as np
import matplotlib.pyplot as plt
A = np.array([[0.3, 0.7],
[0.6, 0.4]])
num_iterations = 10
x = np.array([-1.0, 0])
plt.figure(figsize=(8, 6))
plt.xlim(-1.5, 1.5)
plt.ylim(-1.5, 1.5)
plt.xlabel('X-axis', fontsize=12)
plt.ylabel('Y-axis', fontsize=12)
plt.quiver(0, 0, x[0], x[1], angles='xy', scale_units='xy', scale=1, color='black', linewidth=2, label='Input Vector')
for i in range(num_iterations):
x = np.dot(A, x)
plt.quiver(0, 0, x[0], x[1], angles='xy', scale_units='xy', scale=1, color=f'C{i}', linewidth=0.2, label=f'Iteration {i + 1}')
eigenvalues, eigenvectors = np.linalg.eig(A)
dominant_eigenvector = eigenvectors[:, np.argmax(eigenvalues)]
plt.quiver(0, 0, dominant_eigenvector[0], dominant_eigenvector[1], angles='xy', scale_units='xy', scale=1, color='r', linewidth=2, label='Dominant EigenVector')
plt.legend(fontsize=10)
plt.title('Convergence to Dominant EigenVector', fontsize=18)
plt.grid(True)
plt.tight_layout()
plt.show()
次回予告
本記事では,ネットワークの中心性を考える上で必要になる線形代数の知識をまとめました.基礎的なところなので,何に役立つのかよくわからず辛い部分ですが,辛抱してここまで読んでくださった方はありがとうございます.連載のvol.5以降(作成中)でここで学んだことが活きてくるので,応用に興味がある方はぜひそちらもご覧になってください.間違いや誤植などがあれば,ご連絡いただけると幸いです.
次回は,ネットワーク分析ないしネットワーク科学の数学的な基礎になっているグラフ理論を取り上げます.用語の確認がメインなので,今回ほどのボリュームにはならないと思います.
参考文献

Discussion