zkSNARKs -vol.3 ~さまざまなプロトコルについて(PLONK)~

Ethereum foundationが主催するPSE’s Summer Contribution Programに、この度参加しました。そこでZKPについて、どのような学びがあったかを書いていきます。全体感についてはこちらです。
https://zenn.dev/mameta29/articles/0cb3b96dadcf92

今回は Module4 で学んだ zkSNARKs についての3つ目の記事です。全体で3部構成です。概要から数学的にどのような仕組みでゼロ知識証明を実現しているかまで体系的に記述していきたいと思います。正直このモジュールが一番学びごたえのある難しいものでした。

• 1つ目の記事
• 2つ目の記事

zkSNARKs とは

zkSNARKsは「Zero-Knowledge Succinct Non-Interactive Argument of Knowledge」の略です。

• Zero-Knowledge（ゼロ知識）：証明者は、ある命題が真であることを証明するが、それ以外の情報（命題の内容など）を明らかにする必要はない。
• Succinct（簡潔）：証明は非常に小さいサイズで、迅速に検証可能。
• Non-Interactive（非対話型）：一度生成された証明は、証明者と検証者の間で対話なしに検証できる。

つまり、非対話的にゼロ知識証明を構築でき、ブロックチェーンでのトランザクションの秘匿化やイーサリアムのスケーリング問題のソリューションとして応用することができます。

このzkSNARKsの構築は複雑で以降下記のトピックにて3回に分けて説明します。最後となる今回は「5. PLONK」についてです。

1. Homomorphic Hiding(HH，準同型ハイディング)とは？
2. 算術回路からQAPへ
3. Pinocchio Protocolとは？
4. Groth16
5. PLONK

PLONK

PLONKは比較的新しいのzkSNARKの証明システムである。Groth16のようなこれまでのzkSNARKはcircuitごとにセットアップを行っていたがPLONKでは、一度開始すればすべての回路で再利用できるというところが大きな特徴。

そもそもTrusted Setupとは

zk-SNARKsを使用するために必要な公開パラメータを生成するプロセス。この公開パラメータには、ランダム値や暗号学的なセキュリティに関する値が含まれる。

Ceremonyというので複数人が参加可能で、ロジック的には信頼できる人が1人でもいれば、そのTrusted Setupは信頼できるものとなる。

だが証明(Proof)サイズが大きいなどのデメリットもある。今回はPLONKを使ってどのように計算を証明するかを順を追って説明していきたい。
構成は下記のようになっています。

1. Arithmetic Circuit (算術回路)
2. Costraint System
3. Polynomial
4. Polynomial Commitment
5. PLONK

1. Arithmetic Circuit (算術回路)

これまでのzk-SNARKと流れは一緒で、やりたいことは「特定の計算が適切に実行されたことを証明すること」で、そのために、証明したい命題を適切な「形式」に変換して演算できるようにしていく。この考え方は1つ目の記事で説明したQAPと同じである。ただその方法が異なるだけということを念頭にいれておくと良いかと思います。

ここですることは、方程式をArithmetic Circuitと呼ばれる「加算と乗算の2種類のゲートで構成されるCircuit」に直すこと。今回の例でも1つ目の記事同様、方程式：P(x) = x³ + x + 5 = 35を例に見ていく。
P(x) = x³ + x + 5 = 35をArithmetic Circuitに直すと下記のような図になる。

https://xiaohuiliu.medium.com/how-plonk-works-part-1-bc8050f4805e より

2. Constraint System（制約システム）

Arithmetic CircuitをConstraint Systemに変換する。circuitの制約には2つのカテゴリーがある。

1. Gate Constraints（ゲート制約）
2. Copy Constraints（コピー制約）

1. Gate Constraints（ゲート制約）

circuitの各ゲート内の制約。上のcircuitには4つのゲートがあり、次のような制約になる。
(上記の図の入力と出力を表しているだけ)

a0 * b0 = c0
a1 * b1 = c1
a2 + b2 = c2
a3 + b3 (5) = c3 (35) -> a3 = 30

PLONKでは、すべての制約は以下の形に正規化/標準化される。
QL a + QR b + Qo c + QM ab + QC = 0

• L -> Left
• R -> Right
• O -> Output
• M -> Multiply
• C -> Constants (定数)
• a、b、cはそれぞれゲートの左、右、出力wire(ゲートの導線をwireという)

加算や乗算はQを調整することで表せられる。
例えば加算ゲートにするには...
QL = 1, QR = 1, QO = -1, QM = 0, QC=0を入力すると
QL a + QR b + Qo c + QM ab + QC = 0は
a + b - c = 0と加算で表現可能。

乗算ゲートにするには
QL = 0, QR = 0, QO = -1, QM = 1, QC=0とすればよい。

これを例に当てはめると下記のようになる。

(0)a0 + (0)b0 + (-1)c0 + (1)a0b0 + (0) = 0
(0)a1 + (0)b1 + (-1)c1 + (1)a1b1 + (0) = 0
(1)a2 + (1)b2 + (-1)c2 + (0)a2b2 + (0) = 0
(1)a3 + (0)b3 + (0)c3 + (0)a3b3 + (-30) = 0

Qをベクトル形式で書き直すことができる
QL=(0,0,1,1)、QR=(0,0,1,0)、QO=(-1,-1,-1,0)、QM=(1,1,0,0)、QC=(0,0,0,-30)。

Qベクトルはselector(セレクタ)と呼ばれ、回路構造、すなわちプログラムを符号化する。

同様に、すべてのa、b、cをベクトルに集めることができる

a = (a0, a1, a2, a3), b = (b0, b1, b2, b3), c = (c0, c1, c2, c3)。

これらのベクトルをwitness assignmentsと呼ぶ
ユーザー入力から派生するすべてのwireの値を表す。

2. Copy Constraints（コピー制約）

wireが同じ値を含むことを保証する。ゲート0の出力はゲート1の左入力と同じになる。

• a0 * b0 = c0
• c0 = a1
  さらに、a0 = b0 = b1 = a2のように、wireを括ることもできる。

https://xiaohuiliu.medium.com/how-plonk-works-part-1-bc8050f4805e より

Permutation check（順列チェック）

まず、1つのベクトル内(例：a同士の制約)のコピー制約（a0 = a2）を考える。

σ(i)：並べ替えられたベクトルのi番目の要素の新しいインデックスである。この場合、下図が示すようにσ=(2, 1, 0, 3)となり、a0とa2が入れ替わることになる。

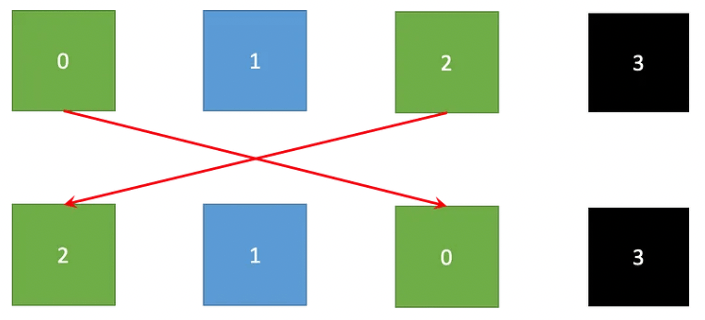
図中の色はwireの値を表す。順列化されたブロックの先頭が元のブロックと同じ色であれば、コピー制約が満たされる。

3. Polynomials

インデックスをx座標として使用することで、ベクトルを点のリストに変換することができる。例えば、QLは上記で「QL=(0,0,1,1)」だった。これは x = index = 0, 1, 2, 3 で、yに値「QL=(0,0,1,1)」を取ると、 (0, 0)、(1, 0)、(2, 1)、(3, 1)に変換できる。
これらの点を通る一意な3次数の多項式がある。{0, 1, 2, 3}をEvaluation Domain（評価ドメイン）と呼ぶ。QLは Evaluation Form（評価形式）でありCoefficient Form（係数形式）はラグランジュなどの補間を用いて求めることができる。

Evaluation Domain（評価ドメイン）

多項式の値を評価または計算するためのx座標のセット

Evaluation Form（評価形式）

多項式を評価ドメインの点で評価する形式
例：次の多項式を評価ドメイン {0, 1, 2, 3} で評価する場合
P(x)=2x^3 − x^2 + 3x − 5
多項式 P(x) は評価ドメインの各点で評価され、その結果は評価形式で表現される

• P(0)=2⋅0^3 − 0^2 + 3⋅0 − 5 = −5
• P(1)=2⋅1^3 − 1^2 + 3⋅1 − 5 = −1
• P(2)=2⋅2^3 − 2^2 + 3⋅2 − 5 = 15
• P(3)=2⋅3^3 − 3^2 + 3⋅3 − 5 = 53

Coefficient Form（係数形式）

多項式はその係数によって直接表現される
係数形式：
Q(x) = (an)x^n + (an−1)x^(n−1) + … + (a1)x + (a0)
例：
Q(x) = 2x^3 − x^2 + 3x − 5
係数 a3 = 2, a2 = −1, a1 = 3, a0 = -5 と明示的に示されている

そもそも「多項式を評価」って？

多項式を評価するとは、与えられた多項式に特定の値（または変数）を代入し、その結果を計算すること。

補間による係数形式の取得とは「評価形式 -> 係数形式」これをしているにすぎない。
単にそれぞれの評価の座標の値を代入して、連立方程式で求める方法もあるが大変。なので補間というものをすれば効率よく求められる。（ラグランジュ補間など）

ラグランジュ補間の簡単な例についてはこちらの記事にあるので参照ください。

$$Q_L(x) = -\frac{1}{3}x^3 + \frac{3}{2}x^2 - \frac{7}{6}x$$

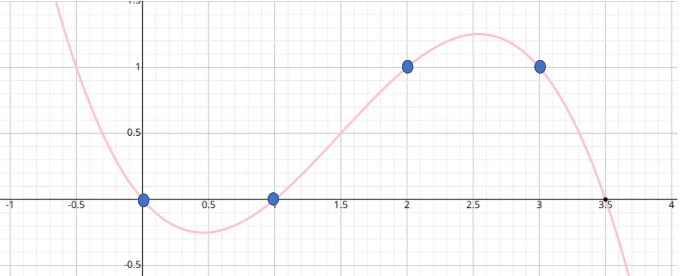
f(x)を下記のように定義し他のベクトルについても同じドメインを評価していく。

$$f(x) = Q_L(x)a(x) + Q_R(x)b(x) + Q_O(x)c(x) + Q_M(x)a(x)b(x) + Q_C(x)$$

0で評価する f(0)

$$\begin{aligned} f(0) &= Q_L(0)a(0) + Q_R(0)b(0) + Q_O(0)c(0) + Q_M(0)a(0)b(0) + Q_C(0) \\ &= (0)a_0 + (0)b_0 + (-1)c(0) + (1)a_0b_0 + (0) \\ &= 0 \end{aligned}$$

同様に、fを1、2、3で評価することができ、その結果はすべて0となる。

制約がすべて満たされるのは、次のことが成り立つ場合だけ

$$f(x) = 0, \forall{x}\in\{0, 1, 2, 3\}$$

式の意味：x が{0, 1, 2, 3}の範囲で f(x)=0が全て成り立つという意味

すべての制約を1つの多項式f(x)に圧縮し、次のように表すことができる。

$$f(x) = Z(x)H(x)$$

$$Z(x) = x(x-1)(x-2)(x-3)$$

これは、0、1、2、3がf(x)の根（値が0になる点）だからである。f(x)をZ(x)で余りなく割るような多項式H(x)が存在する限り、ゲート制約が成り立つことを確認できる。Z(x)は"the vanishing/zero polynomial" 消失・ゼロ多項式、H(x)は "the quotient polynomial" 商多項式と呼ばれる。

別の多項式g(x)を定義することができる：

$$g(x) = f(x) - Z(x)H(x) = 0$$

g(x)がどこでも0であること、すなわちゼロ多項式であることを示せばよい。

Schwartz-Zippel lemma

Schwartz-Zippelの補題は、多項式理論の中で重要なものらしい。

次のような多項式 f(x) がある。

$$f(x) = a_0{x^d} + a_1{x^{d-1}} + ... + a_{d-1}{x} + a_d$$

$a_i$は係数、$d$は多項式の次数、$x$は変数

Schwartz-Zippelの補題
「多項式 $f(x)$ が非ゼロ多項式で、体 $F$（有限の要素を持つ数学的な構造）のサイズが $n$ の場合、ランダムに選んだ $s$ に対して、$f(s)=0$ となる確率は $d/n$ を超えない。」

つまり $d$ は$f(x)$の次数で、最大で$d$個の値（$f(x)=0$の解）しか持たない。なのでランダムに$s$を選んだ場合、$f(s)=0$になる確率は$d$に対して$n$が十分に大きい場合、非常に小さいことが示される。

あるランダムな点で多項式を評価し、その評価が0であった場合、その多項式は圧倒的な確率でどこでも0であることを意味する。

また、あるランダムな点で2つの多項式を評価し、それらが等しければ、ほぼ確実にどこでも等しいということになる。

4. Polynomial Commitment Scheme（多項式コミットメント）

多項式P(x)が0であることを証明するために、Polynomial Commitment Scheme(PCS)多項式コミットメントスキームを使う。PCSはある多項式P(x)の「ハッシュ」のようなものとみなすことができ、commiter（証明者）は多項式Pを明らかにすることなく、Pが特定の点で特定の値に評価されることを証明できる。

PCSは、証明者と検証者の間で3ラウンドで構成される

https://xiaohuiliu.medium.com/how-plonk-works-part-1-bc8050f4805e より

1. Commit： prover（証明者）はある多項式Pをコミットし、それを検証者に送信する。
2. Challenge： 検証者は多項式Pをランダムな点sで評価することを要求し、sを証明者に送信する。
3. Open：証明者は点sでのPの評価値yを計算し、評価のproofとともに結果を検証者に送り返す。検証者はproofをチェックし、それが有効であればP(s) = yと結論する。多項式の方程式自体はランダムな値で評価することで効率的に検証される。

g(x)がゼロであることを証明するためにPCSを使うことができる。PLONK論文では、ペアリングに基づくKateコミットメントを用いている。他のPCSを使うこともできる。

Grand product（大積）

まずランダムな値 $β$ と $γ$を取得し、 $f$と$g$関数を定義する。

$$\begin{aligned} f(i) &= a_i + iβ + γ \\ g(i) &= a_i + σ(i)β + γ \end{aligned}$$

ここで$σ(i)$は順列化したもの。(Copy Constraintsにて)
以下の式が成り立つ場合に限り、Permutation Checkはパスする

$$\prod^3_{i=0}f(i)/g(i) = 1$$

この左辺の式が表題の "Grand product（大積）"という。
上の例でa0 = a2の時、Grand productが成り立つか見てみる。下記のようになる。

$$\dfrac{(a_0 + 0β + γ)(a_1 + β + γ)(a_2 + 2β + γ)(a_3 + 3β + γ)}{(a_0 + 2β + γ)(a_1 + β + γ)(a_2 + 0β + γ)(a_3 + 3β + γ)} = 1$$

これは分子分母ともに$(a_1 + β + γ)$と$(a_3 + 3β + γ)$は相殺できる。

すると残るのは下記のようになる。

$$\dfrac{(a_0 + 0β + γ)(a_2 + 2β + γ)}{(a_0 + 2β + γ)(a_2 + 0β + γ)} = 1$$

a0 = a2なので$(a_0 + 0β + γ)$と$(a_2 + 0β + γ)$、$(a_2 + 2β + γ)$と$(a_0 + 2β + γ)$がそれぞれ相殺できるため、Grand productの値は 1 となり式が成り立ち Permutation Checkがパスできる。

Proof

Schwartz-Zippelのジレンマは、2つの多項式がランダムな評価点で等しい場合、この2つの多項式は高い確率でどこでも等しいというもの。ここで2つの多項式を考えてみる。

$$P_1(x) = \prod^3_{i=0}(a_i + iβ + x) \\ P_2(x) = \prod^3_{i=0}(a_i + σ(i)β + x)$$

これらの多項式はランダムなγで等しいと仮定される。つまり同じ根を持つと考えられる。

$$P_1(γ) = P_2(γ)$$

$P_1$のj番目の根と$P_2$のi番目の根が一致すると仮定すると下記の式が成りたつ。

$$a_j + jβ + x = a_i + σ(i)β + x \\ a_j + jβ = a_i + σ(i)β$$

新たな多項式$R_1$と$R_2$を下記のように定義する。

$$R_1(x) = a_j + jx \\ R_2(x) = a_i + σ(i)x$$

これらの多項式はランダムなβで等しいと仮定されるので$R_1(β) = R_2(β)$となる。
$a_i = a_j$が成り立つことが示される。

なのでGrand product（大積）が1の場合、順列条件 σ(i) = j が成り立つとき ai = aj となる。
この証明により、大積が1の場合、順列チェックがパスし、順列内の要素が等しいことが示される。

Polynomial

Roots of unity（単一根）

ベクトルを多項式に変換する際の評価ドメイン"H"として、ベクトルindex {0, 1, 2, ..., n-1}を使用したが、任意の領域を使用することができる。

PLONKでは、性能向上のため、多項式補間に使用するドメインは単一根で構成されます。体のn番目の単根は、ω^n = 1を満たす体の要素ωである。nはベクトルのサイズで、この場合は4である。Hは{ω⁰, ω¹, ω², ω³ }である。

Accumulator

ここがよくわかってないので調べてる。

評価ベクトル P を下記のように定義する。

$$P(ω) = 1 \\ P(ω) = \prod_{j<i}f(j)/g(j), i \in \{1..n\}$$

Pは再帰的に書き換えることができるので、grand product（大積）を累積する。

$$P(ω^{i+1}) = P(ω^i)f(i)/g(i)$$

P(x)のようなものが存在すれば、grand product （大積）方程式が成り立つことがわかる。

$$\prod^3_{i=0}f(i)/g(i) = 1$$

$$P(ω^n) = \prod_{i=0}^{n-1}f(j)/g(j) = P(1) = P(ω^0) = 1$$

上記の$P(ω^{i+1}) = P(ω^i)f(i)/g(i)$は両辺$g(i)$を乗算すると下記と等しい。

$$P(ω^{i+1})g(i) = P(ω^i)f(i)$$

P(x)、f(x)、g(x)は、評価ドメイン H {ω⁰, ω¹, ω², ω³ }上の補間を用いて求めることができる。次の多項式がドメインH上で成り立つ。

$$P(xω)g(i) = P(x)f(x)$$

$$f(x) = a(x) + xβ + Δ \\ g(x) = a(x) + σ(x)β + Δ \\$$

$$P(xω)g(x) - P(x)f(x)= Z(x)H(x)$$

$$Z(x) = (x-ω^0)(x-ω^1)(x-ω^2)(x-ω^3)$$

Copy constraints across vectors

ベクトル a, b, c の間には、コピー制約が存在する。具体的には、a2 と b0 が等しいこと (a2 = b0)、および a1 と c0 が等しいこと (a1 = c0)などがある。

https://xiaohuiliu.medium.com/how-plonk-works-part-1-bc8050f4805e より

コピー制約を処理するために、ベクトル a、b、c を1つの大きなベクトルに結合する。この大きなベクトルのサイズ n は 12 (要素4つ × ベクトル3つ(a, b, c))になる。これにより、異なるベクトル間でのコピー制約を処理しやすくなる。
$a\{0, 1, 2, 3\}$ $b\{0, 1, 2, 3\}$ $c\{0, 1, 2, 3\}$ それぞれを結合して

$i: \{0(a_0), 1(a_1), 2(a_2), 3(a_3), 4(b_0), 5(b_1), 6(b_2), 7(b_3), 8(c_0), 9(c_1), 10(c_2), 11(c_3)\}$

• $i{1(a_1)} = i{8(c_0)} = 9$
• $i{0(a_0)} = i{2(a_2)} = i{4(b_0)} = i{5(b_1)} = 3$
• $i{3(a_3)} = i{10(c_2)} = 30$
• $i{6(b_2)} = i{9(c_1)} = 27$

$σ(i): \{2(a_2), 8(c_0), 4(b_0), 10(c_2), 5(b_1), 0(a_0), 9(c_1), 7(b_3), 1(a_1), 6(b_2), 3(a_3), 11(c_3)\}$

上記Grand product（大積）は下記のようになる。

$$\begin{aligned} f(i) &= a_i + iβ + γ \\ g(i) &= a_i + σ(i)β + γ \end{aligned}$$

$$\begin{aligned} f(i) &= (a_i + iβ + γ)(b_i + iβ + γ)(c_i + iβ + γ) \\ g(i) &= (a_i + σ(i)β + γ)(b_i + σ(i)β + γ)(c_i + σ(i)β + γ) \end{aligned}$$

残りのステップは、単一ベクトル内のコピー制約を強制するステップと同様。

PLONKまとめ

PLONKがどのような仕組みか要約すると、証明すべきプログラムPが与えられると

• まずそれを算術回路に変換
• 次にゲート制約やコピー制約を含む一連の制約に変換
• それらを多項式に変換
• 最後に、PCSを用いて多項式の同一性を簡潔に検証する