💨

zkSNARKs - vol.2 ~さまざまなプロトコルについて(Pinocchio ProtocolとGroth16)~

2023/11/16に公開

Ethereum foundationが主催するPSE’s Summer Contribution Programに、この度参加しました。そこでZKPについて、どのような学びがあったかを書いていきます。全体感についてはこちらです。

今回は Module4 で学んだ zkSNARKs についての2番目の記事です。全部で3部構成です。概要から数学的にどのような仕組みでゼロ知識証明を実現しているかまで体系的に記述していきたいと思います。正直このモジュールが一番学びごたえのある難しいものでした。

zkSNARKs とは

zkSNARKsは「Zero-Knowledge Succinct Non-Interactive Argument of Knowledge」の略で、特定の計算が正しく行われたことを証明する方法のことです。
主な特徴としては下記のようなものがあります。

Zero-Knowledge（ゼロ知識）：証明者は、ある命題が真であることを証明するが、それ以外の情報（命題の内容など）を明らかにする必要はない。
Succinct（簡潔）：証明は非常に小さいサイズで、迅速に検証可能。
Non-Interactive（非対話型）：一度生成された証明は、証明者と検証者の間で対話なしに検証できる。

つまり、非対話的にゼロ知識証明を構築でき、ブロックチェーンでのトランザクションの秘匿化やイーサリアムのスケーリング問題のソリューションとして応用することができます。

このzkSNARKsの構築は複雑で以降下記のトピックにて2回に分けて説明します。この2番目の記事では「3. Pinocchio Protocolとは？」「4. Groth16」についてです。今回も主に「PSE’s Summer Contribution Program」に参加した人たちの発表内容を要約する形で書いていこうと思います。

Homomorphic Hiding(HH，準同型ハイディング)とは？
算術回路からQAPへ
Pinocchio Protocolとは？
Groth16
PLONK

3. The Pinocchio Protocolとは？

The Pinocchio Protocolは、zkSNARKsを実現するための具体的な方法の一つとして実装されたものでその特徴を下記の順序で説明していきます。

KEAとは？
KEAをQAPに適用する
The Pinocchio Protocolで検証したいこと

1. KEAとは？

KEAはThe Pinocchio Protocolで使用される数学的な仮定です。具体的には、ある数Qが基数Pの指数kによって生成された場合（Q=P^k）、そのQを生成した者は指数kを「知っている」と見なされる、という仮定。KEAは、証明者が特定の計算の結果を知っていることを前提としており、この仮定はzkSNARKsのようなゼロ知識証明システムの設計において重要な役割を果たす。離散対数問題の計算上の困難さを利用し、特定の状況での知識や情報の存在を仮定するものといえる。

KEAでできること：上記の点PとQのiを係数とした線形結合であるRとSがあった時、またS=R^kが成り立つようなRとSをkを知らずに求めることができる。
→つまり線型結合を成り立たせる係数iを知っているということになる。

PSE発表者資料より

2. KEAをQAPに適用する

上述したKEAの仮定をQAPに適用するということをしていく。

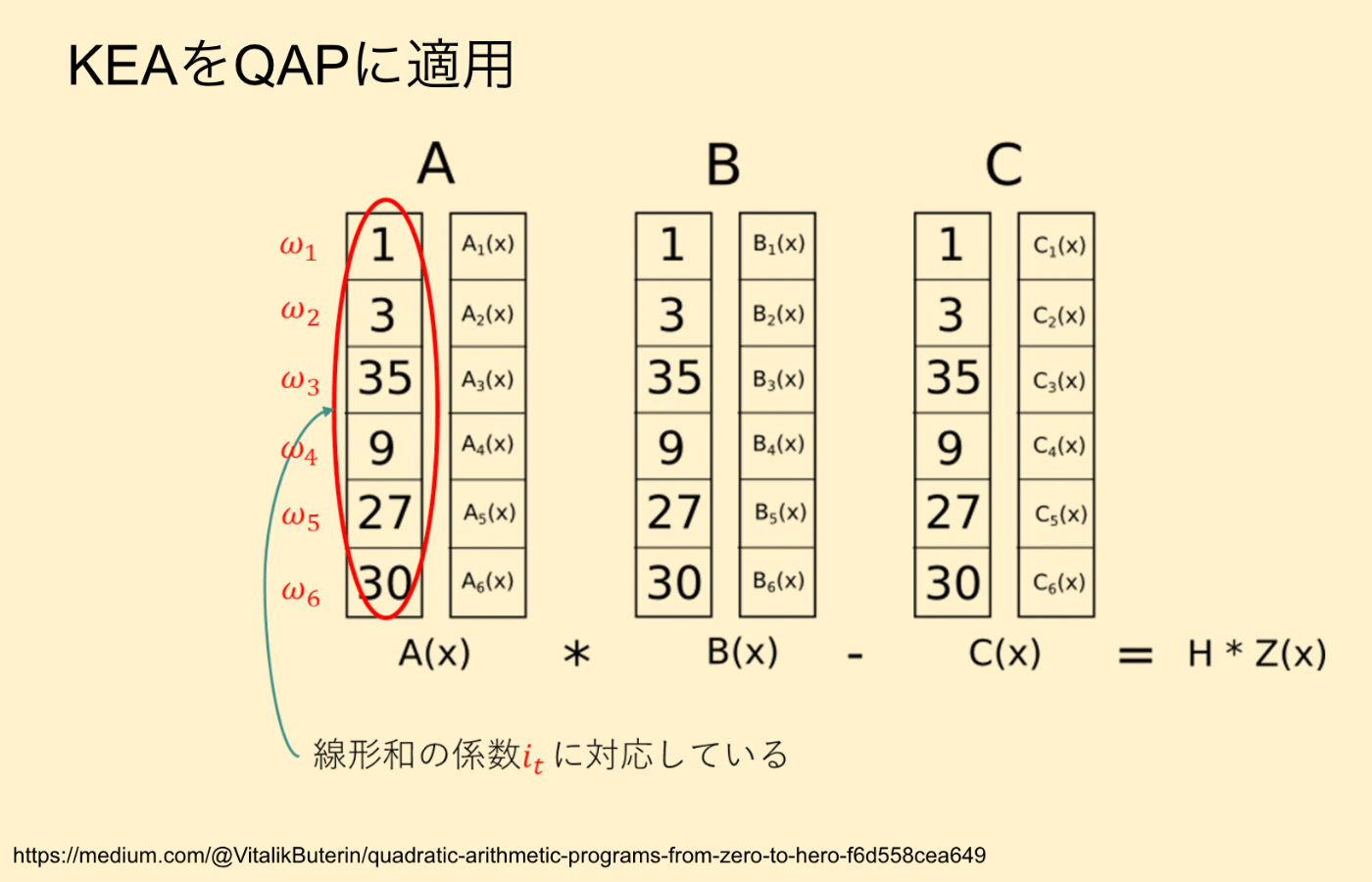
PSE発表者資料より

この図にあるω1...ω6を先ほどの係数iとし、A1~A6の線型結合として考えていくことでKEAをQAPに適用していく。

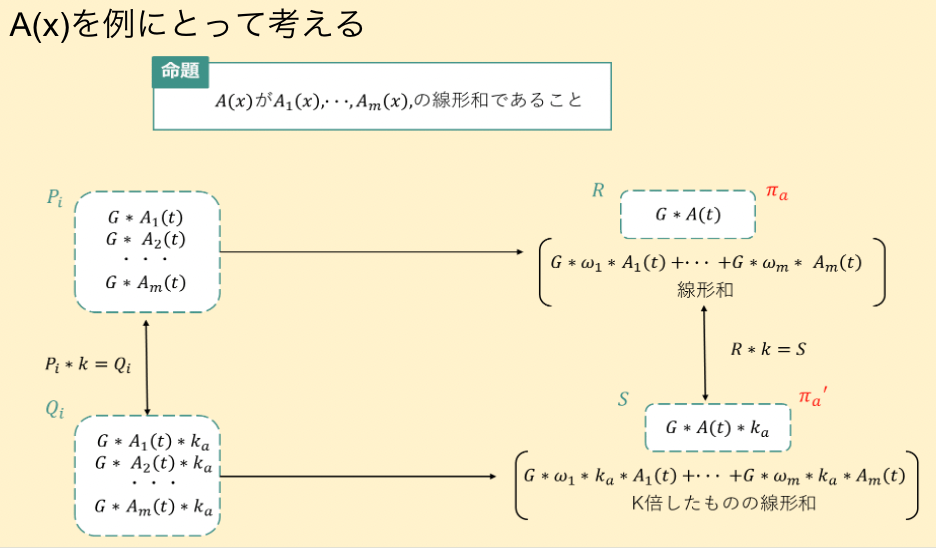
PSE発表者資料より

A(x)において正しいR * k = Sを証明できれば係数となっているω1...ωmの値を知っていることの証明になる。そしてその係数が他のB(x), C(X)でもなり立つことが証明できたらよい。

PSE発表者資料より

3. The Pinocchio Protocolで検証したいこと

The Pinocchio Protocolで検証したいことは主に3つです。

PSE発表者資料より

こちらの図で示したA(x), B(x)そしてC(x)において下記が成り立つことです。

A(x), B(x), C(x)がそれぞれ線形和かどうか調べる
A(x), B(x), C(x)が同じ係数の線形和になっているか調べる
(ここまでは上述2で記載したところです。)
A(x) * B(x) - C(x) = H(x) * Z(x)
(最後に使用したwitnessの値が正しいかどうかを検証)

4. Groth16

Groth16はThe Pinocchio Protocolと同様zk-SNARKsの実装の1つですが、The Pinocchio Protocolとの大きな違いは、証明(Proof)サイズを大幅に小さくしたところにあります。なのでブロックチェーンではよくこのプロトコルが使用されます。
下記の順序に従って説明していきます。(詳細な部分には踏み込まないのでご了承ください。)

Groth16の基本的な仕組み
Pinocchio との違い
検証の準備
検証

1. Groth16の基本的な仕組み

Trusted Setup

計算の有効性を検証するためのパラメータを生成します。詳細はここでは省きますが、zk-SNARKsを使用するために必要な公開パラメータを生成するプロセスのことをTrusted Setupといいます。この公開パラメータには、ランダム値や暗号学的なセキュリティに関する値が含まれる。Ceremonyというので複数人が参加可能で、ロジック的には信頼できる人が1人でもいれば、そのTrusted Setupは信頼できるものとなる。