🦁

zkSNARKs -vol.1 ~数学的背景を順を追う~

2023/11/16に公開

Ethereum

zksnark

tech

Ethereum foundationが主催するPSE’s Summer Contribution Programに、この度参加しました。そこでZKPについて、どのような学びがあったかを書いていきます。全体感についてはこちらです。

今回は Module4 で学んだ zkSNARKs についての1つ目の記事です。全部で3部構成です。概要から数学的にどのような仕組みでゼロ知識証明を実現しているかまで体系的に記述していきたいと思います。正直このモジュールが一番学びごたえのある難しいものでした。

zkSNARKs とは

zkSNARKsは「Zero-Knowledge Succinct Non-Interactive Argument of Knowledge」の略です。

Zero-Knowledge（ゼロ知識）：証明者は、ある命題が真であることを証明するが、それ以外の情報（命題の内容など）を明らかにする必要はない。
Succinct（簡潔）：証明は非常に小さいサイズで、迅速に検証可能。
Non-Interactive（非対話型）：一度生成された証明は、証明者と検証者の間で対話なしに検証できる。

つまり、非対話的にゼロ知識証明を構築でき、ブロックチェーンでのトランザクションの秘匿化やイーサリアムのスケーリング問題のソリューションとして応用することができます。

このzkSNARKsの構築は複雑で以降下記のトピックにて3回に分けて説明します。今回は「1. Homomorphic Hiding(HH，準同型ハイディング)とは？」と「2. 算術回路からQAPへ」についてです。今回はまた主に「PSE’s Summer Contribution Program」に参加した人たちの発表内容を要約する形で書いていこうと思います。

Homomorphic Hiding(HH，準同型ハイディング)とは？
算術回路からQAPへ
Pinocchio Protocolとは？
Groth16
PLONK

1. Homomorphic Hiding(HH，準同型ハイディング)とは？

以下の性質を満たすEのことをHomomorphic Hidingという。

一方向性：E(x)からxを見つけるのが難しい
単射性：x != y ならば E(x) != E(y)

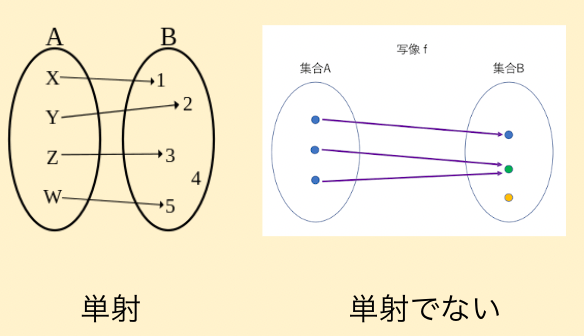
PSE発表者資料より
準同型性：E(x)とE(y)からxとyの算術式のHHを求められる。
-> E(x)*E(y)=E(x+y)
計算例：E(x) = g^x，P(x) = x^3 - 3x^2 + 2xとすると
E(P(x)) = E(x^3 - 3x^2 + 2x)
= g^(x^3 - 3x^2 + 2x)
=E(x^3) * E(x^2)^(-3) * E(x)^2

2. 算術回路からQAPへ

そもそも何がしたいかといえば、特定の計算が適切に実行されたことを証明すること。
zk-SNARKはどんな計算問題にも直接適用することはできない。むしろ、問題を適切な「形式」に変換して演算する必要がある。この形式はQAP「Quadratic Arithmetic Program(四則演算プログラム)」と呼ばる。その変換の過程を説明していく。

方程式 -> 算術回路
算術回路 -> R1CS
R1CS -> QAP

以降Vitalikの記事も参照していく。

1. 方程式 -> 算術回路

まず、問題を算術回路と呼ばれるものに変換する必要がある。これにより、方程式を「Flatting(平坦化)」して、より単純な一連の方程式にすることができる。語弊を恐れずにいえば、複雑な計算を2つの計算に分けていく作業といえる。以降x^3 + x + 5 = 35を例題として進める。
x^3 + x + 5 = 35を算術回路に変換すると下記のようになる。

sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5

2. 算術回路 -> R1CS

算術回路をR1CS（Rank-1 Constraint System）に変換する過程を説明していく。R1CSは、計算を行列とベクトルの形式で表現するためのシステムで単純な構成要素に分解していくことが目的である。

R1CSの基本：R1CSは三つのベクトル（a, b, c）のシーケンスで構成され、解となるベクトル s が存在する。このsは、ドット積を用いた方程式 s . a * s . b - s . c = 0 を満たす必要がある。

各ゲートの変換：前トピックで説明した算術回路（+, -, *, / などの基本的な計算操作）は、それぞれ異なる (a, b, c) の三つ組に変換される。ベクトルの長さは、システム内の変数の総数に等しく、特定のゲートによって影響を受ける変数に対応する位置にのみ値が入る。

先ほどの例でいえば変数は6つ存在する（'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'）のでベクトルの長さも6に等しくなる。

sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5

各ゲートの具体例：
1つ目のゲート：x * x = sym_1

a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]

ちなみにこの1が立っているところは先ほどの変数の場所と一致している。
'~one', 'x', '~out', 'sym_1', 'y', 'sym_2' とあるので
aはxの位置、bもxの位置そしてcはsym_1の位置に1がたつ。

解ベクトルが2番目の位置に3、4番目の位置に9を含む場合、解ベクトルの残りの内容に関係なく、点積チェックは3 * 3 = 9に帰着し、合格することがわかります。解ベクトルが2番目の位置に-3、4番目の位置に9を持つ場合、このチェックもパスする。実際、解ベクトルが2番目の位置に7、4番目の位置に49を持つ場合でも、このチェックはパスする。この最初のチェックの目的は、最初のゲートの入力と出力の整合性のみを検証することである。

2つ目のゲート：sym_1 * x = y

a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]

最初のドット積のチェックに似たスタイルで、ここではsym_1 * x = yをチェックしている。

3つ目のゲート：x + y = sym_2

a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]

ここでx + yと加算なので計算方法が少々ことなる。s . a * s . b - s . c = 0を満たすことを考える。なのでaで加算をしてしまい、あとはbで1をかけることで、s . a * s . b - s . c = 0の形を実現する。

4つ目のゲート：sym_2 + 5 = ~out

a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]

ここでは、最後のチェック、~out = sym_2 + 5を評価している。ドット積チェックは、解ベクトルの6番目の要素を取り、最初の要素の5倍を加え（注意：最初の要素は1なので、これは事実上5を加えることを意味する）、3番目の要素と照合する。

inputに応じてwitnessという値は変わる。witnessの入力、出力、内部変数を含むすべての変数への代入は、x=3の場合下記のようになる。
[1, 3, 35, 9, 27, 30]

入力変数の代入x=3から始めて、すべての中間変数と出力の値を計算しながら入れて、上記の平坦化されたコードを「実行」するだけで計算することができる

R1CSの完成形は次のようになる

A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]
B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]

3. R1CS -> QAP

次のステップは、前トピックで作成したR1CSをQAP(Quadratic Arithmetic Program)形式に変換するzz。QAP形式は、ドット積の代わりに多項式を使う以外は、まったく同じロジックを実装している。R1CSでは長さ6の3つのベクトル(a, b, c)からなる4つのグループがあったが、それを次数3の多項式からなる6つのグループにする。つまりR1CSのベクトルを多項式に変換するということ。

R1CSからQAPへの変換には、ラグランジュ補間を用いて多項式を生成する過程が含まれる。ラグランジュ補間は、与えられた点群を通る多項式を見つける方法。各点に対して、その点でのみ特定の値（y座標）を取り、他の点では0を取る多項式を生成し、最終的な多項式はこれらを全て足し合わせたものになる。

例として、点 (1, 3), (2, 2), (3, 4) を通る多項式を見つけることを考える。

最初の点 (1, 3) に対する多項式
- (1, 3), (2, 0), (3, 0)を通る多項式を作る -> (x - 2) * (x - 3)
  
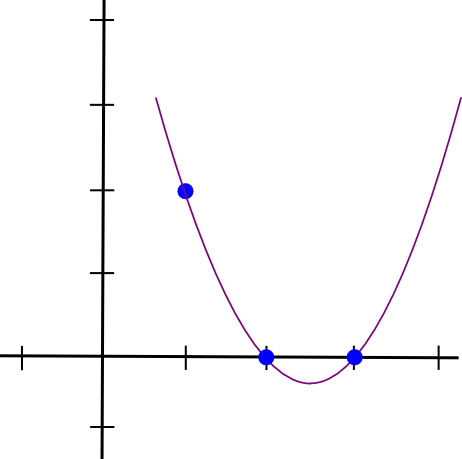
  https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649 より
- これを x=1で解が3になるように調整する
- 最終的な式 -> (x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))
  -> 3/2 * x ^2 - 15/2 * x + 9
他の点についても同様の手順を行い、最終的に全ての多項式を足し合わせる
最終的な多項式は、3/2 * x ^2 - 11/2 * x + 7 になる。

さて、実際に変換する手順は下記のようになる。

A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]

Aベクトルの変換:
例えば、Aベクトルの最初の列 [0, 0, 0, 5] を取り出す。この列の各要素は、4つの異なる制約（R1CS内の行）の最初の要素となっている。
これらの要素を用いて、ラグランジュ補間を行い、対応する多項式を生成する。
この場合、生成される多項式は
5/6 * x^3 - 5 * x^2 + 55/6 * x - 5
となる。

これを2番目, 3番目... 6番目の列も同様に計算すると下記のような結果となる。

1. 5/6 * x^3 - 5 * x^2 + 55/6 * x - 5
2. -2/3 * x^3 + 5 * x^2 - 34/3 * x + 8
3. 0
4. 1/2 * x^3 - 4 * x^2 + 19/2 * x - 6
5. -1/2 * x^3 - 7/2 * x^2 - 7 * x + 4
6. 1/6 * x^3 - x^2 + 11/6 * x - 1

係数として表すと下記のようになる。

[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]

係数を逆順に並べると上記の多項式が出来上がる。
初めの式(5/6 * x^3 - 5 * x^2 + 55/6 * x - 5)は、
0.833 * x^3 - 5 * x^2 9.166 * x - 5と等しい。

同様に、Bベクトル, Cベクトルと計算していくとQAPが完成する。
それぞれの結果はこの通り。

A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]

B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]

C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]

ちなみにこれらの多項式を x = 1 で評価すると、R1CSの元のベクトルの値が得られる。

A results at x=1
0
1
0
0
0
0
B results at x=1
0
1
0
0
0
0
C results at x=1
0
0
0
1
0
0

これらの多項式はこの図のような関係が成り立っている。

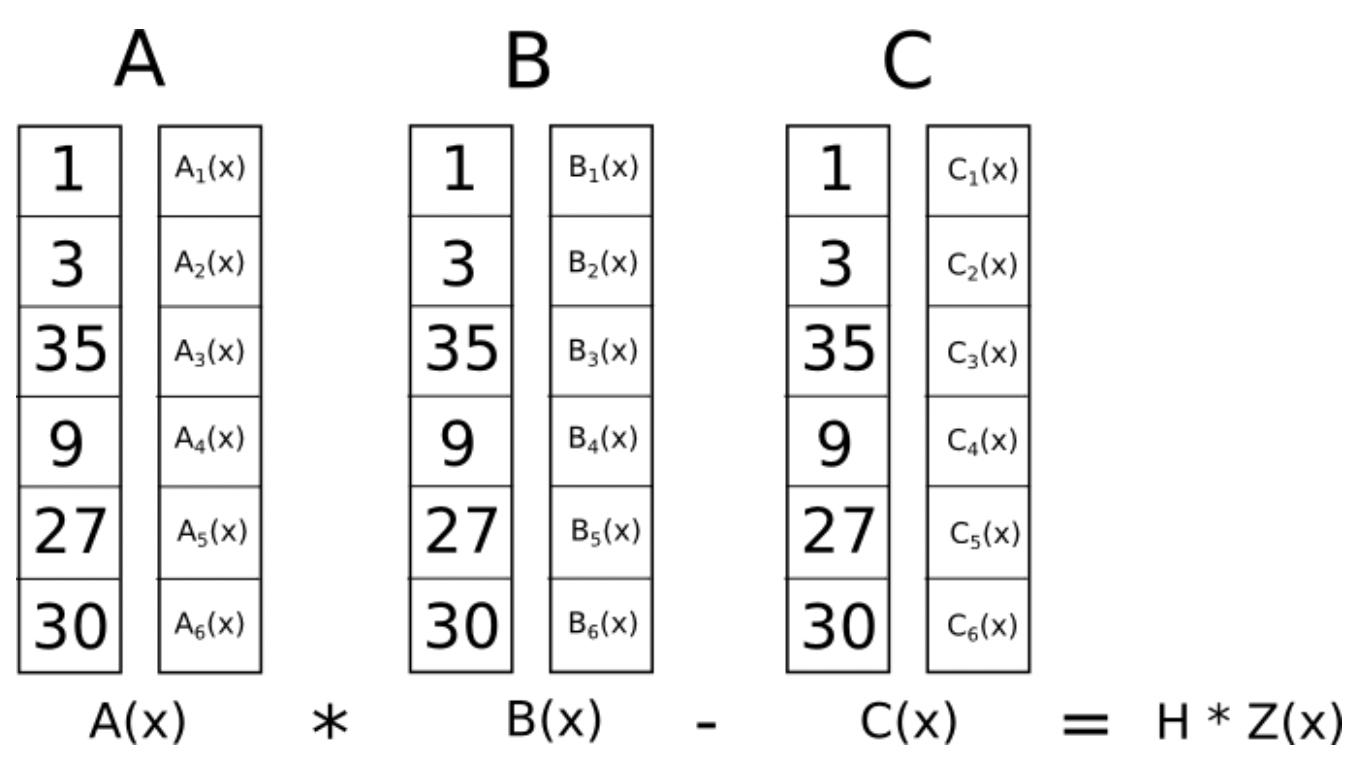
https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649 より

次の記事では「3. Pinocchio Protocolとは？」「4. Groth16」についてです。

「5.PLONK」についてはこちらです。