データ分析 重回帰分析 実践1

前回までの記事です
データ分析 python 相関分析 & 無相関検定
データ分析 python 単回帰分析
データ分析 python 重回帰分析
今回は、別のデータを使用して、より実践ベースで検定を行ってみたいと思います

使用したデータ

あるジュエリーショップのアンケート結果を集めたデータです。

使用したデータ

データは適当に作ったものです

性別	年齢	購入形態	購入の目的	商品のデザイン	納品の迅速さ	サイトの使いやすさ	価格の妥当性	商品への満足度	ショップの雰囲気	スタッフの対応	アフターサービス	包装の状態	満足度
女性	50	プレゼント用	記念日	4	4	4	4	3	4	4	4	4	4
女性	35	自分用	婚約	4	5	4	4	1	1	5	4	1	2
女性	22	プレゼント用	日常使い	1	1	1	4	1	5	1	3	1	3
男性	30	自分用	記念日	3	4	3	4	5	1	4	4	5	3
男性	59	プレゼント用	婚約	4	3	3	3	4	4	3	5	4	4
男性	52	プレゼント用	日常使い	2	3	3	3	2	2	1	3	2	2
男性	10	自分用	記念日	2	5	1	3	3	3	5	5	3	3
女性	19	自分用	婚約	3	5	2	4	2	5	5	5	5	4
女性	24	プレゼント用	日常使い	4	2	3	4	1	1	4	4	1	2
女性	39	プレゼント用	記念日	5	5	5	5	3	5	5	4	5	5
女性	55	プレゼント用	婚約	3	5	5	5	1	3	2	3	4	3
女性	59	自分用	日常使い	1	3	1	3	3	3	4	4	2	2
男性	30	プレゼント用	記念日	1	1	1	1	4	4	4	4	4	3
男性	58	プレゼント用	婚約	2	2	2	2	2	4	3	4	4	3

以下略

テーマ

満足度に寄与する要因をみつける

分析

必要なライブラリをインストールし、データを読み込んでおきます

# グラフに日本語を表示させるためインストール
!pip install -q japanize_matplotlib

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib

import statsmodels.api as sm # 定数項の追加で使用する
from sklearn.preprocessing import StandardScaler # 説明変数の標準化で使用

np.random.seed(0) # 裏で動く乱数を固定（乱数を固定しないと毎回、結果が異なってしまうため固定する）

plt.style.use('seaborn-whitegrid') # グラフのスタイルを固定
plt.rcParams['font.family'] = 'IPAexGothic' # グラフのフォントをIPAexGothicに設定

df = pd.read_csv('/content/drive/MyDrive/jewelry_shop_reviews.csv')
df.head(3)

カテゴリカル変数を数値に変換

カテゴリカル変数を確認

print(df.select_dtypes(include='object').columns)

カテゴリカル変数のユニーク値を確認しておきます

print(df['性別'].unique())
print(df['購入形態'].unique())
print(df['購入の目的'].unique())

カテゴリカル変数は名義尺度ですので One Hot Encoding で数値化します。

df_enc = pd.get_dummies(df, columns=['性別','購入形態','購入の目的'], drop_first=True).astype(int)
df_enc.head(3)

相関分析を行う

まずは散布図を表示してみます

sns.pairplot(df_enc)

今回はあまり役に立ちません・・・

ヒートマップで相関係数を確認してみます

sns.heatmap(df_enc.corr(), annot=True, square=True, vmax=1, vmin=-1, center=0, fmt='.2f')

満足度とは商品のデザインや商品への満足度、ショップの雰囲気、包装の状態などが関係していそうです

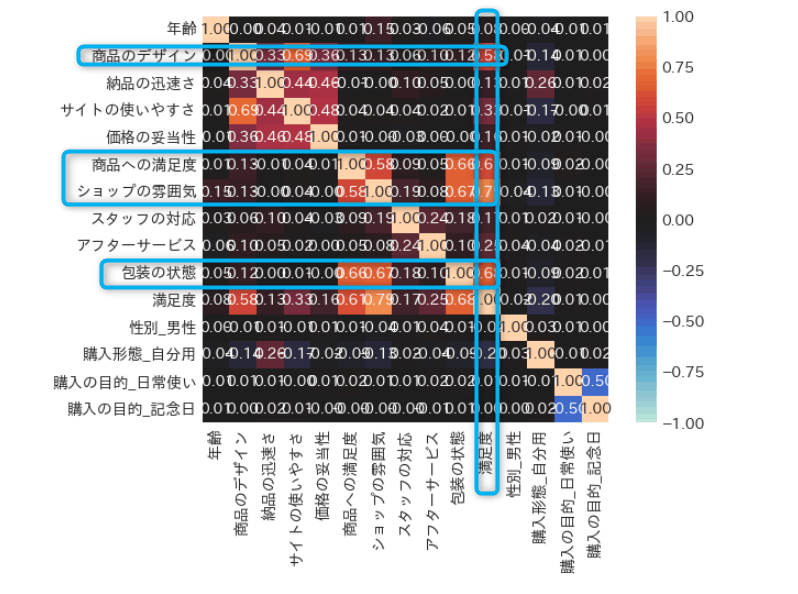
重回帰分析を行う

検定の目的は「満足度に寄与する要因をみつける」です。
ですので、目的変数は「満足度」それ以外の項目を説明変数として重回帰分析を行います

# 目的変数
y = df_enc['満足度']

# 説明変数
x = df_enc.drop('満足度', axis=1)

# 説明変数をスケーリング（標準化）する
scaler = StandardScaler() # インスタンス化
x_std = scaler.fit_transform(x) # 標準化

# 標準化の結果 numpy の ndarray を pandas の DataFrameに変換する
x_std = pd.DataFrame(x_std, columns=x.columns)

# 説明変数に切片（定数項）を追加
x_std_with_const = sm.add_constant(x_std)

# 重回帰分析を行う
res = sm.OLS(y, x_std_with_const).fit()
res.summary()

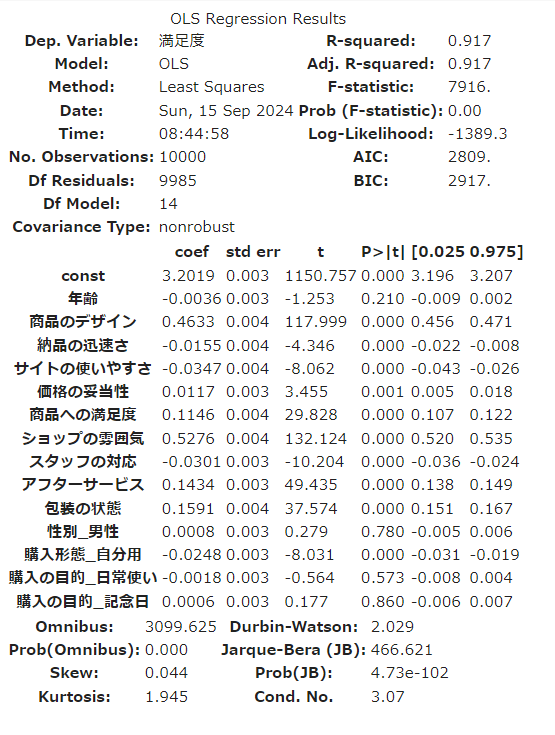
自由度決定係数を確認します。

res.rsquared_adj
# → 0.9172368303546781 比較的良い精度で、元のデータをうまく表現できていると判断できます

標準偏回帰係数、 P値、 t値、 t値（絶対値）のデータフレームを作成します

df_res = pd.DataFrame([res.params[1:], res.pvalues[1:], res.tvalues[1:], np.abs(res.tvalues[1:])], index=['偏回帰係数','P値','t値','t値abs']).T
df_res.sort_values('t値abs', ascending=False)

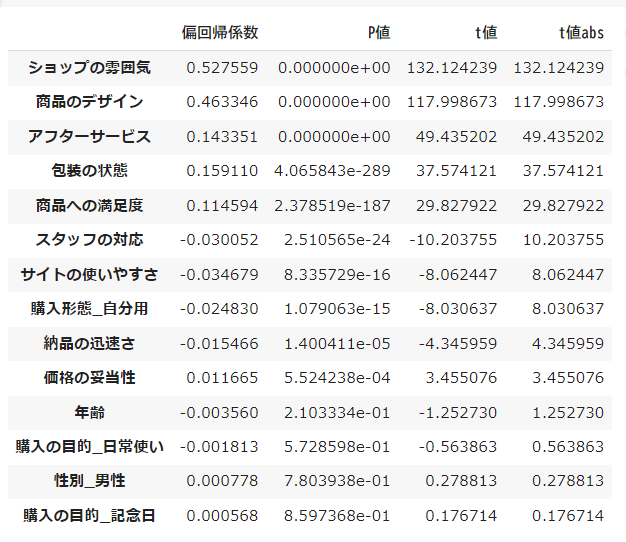
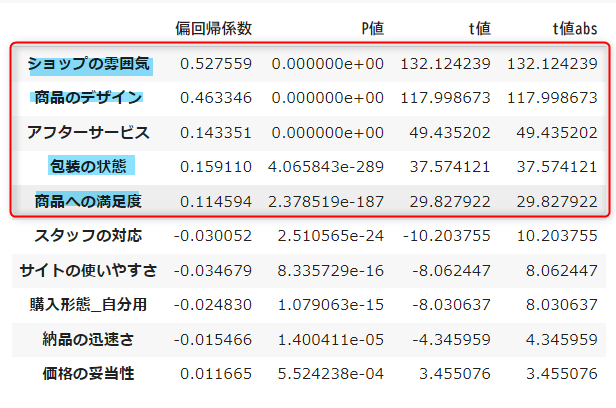
目的変数に影響を与えている可能性が高い以下の条件の変数を抽出し、t値の絶対値順に降順に並べ替えます。

• t値の絶対値が2以上・・・t値が2以上であると、その変数が統計的に有意である可能性が高いと見なされます。
• P値が5%以下・・・有意水準以下（何かしらの影響がある）と考えられます

df_res[(df_res['t値abs'] >= 2) & (df_res['P値'] < 0.05)].sort_values('t値abs', ascending=False)

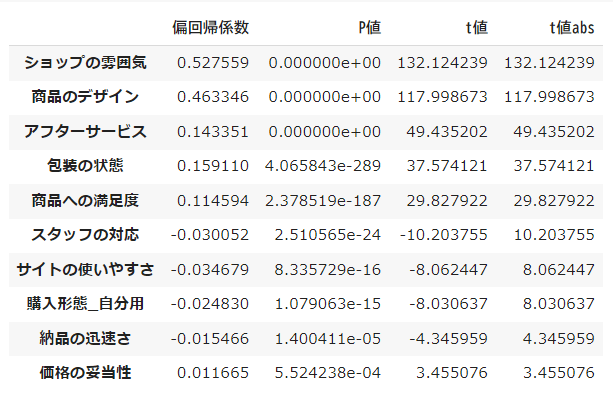
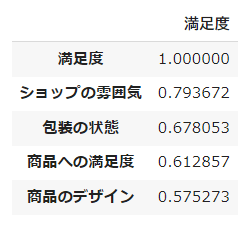
相関係数のうち、0.5（やや相関あり）以上の変数を確認してみます。

corr = df_enc.corr()['満足度']
corr[corr.abs() > 0.5].sort_values(ascending=False)

分析の結果

重回帰分析の結果と相関係数を照らし合わせ、おおよそ以下の項目が満足度に寄与しているのではないかと考えられます。

• ショップの雰囲気
• 商品のデザイン
• アフターサービス
• 包装の状態
• 商品への満足度