📉

データ分析 python 重回帰分析

2024/09/14に公開

Python

データ分析

tech

前回の単回帰分析に続いて多変量解析の重回帰分析について簡単にまとめてみます。
python + google colaboratory で実行しています。

単変量解析
- 相関分析・・・2つの変数が一緒にどのように変化するかを調べる方法
- 単回帰分析・・・1つの独立変数と1つの従属変数を調べる方法
多変量解析
- 重回帰分析・・・複数の独立変数と1つの従属変数を調べる方法

重回帰分析とは

複数の独立変数と1つの従属変数との関係を調べる手法です。
単回帰分析のモデルの式は以下ですが

y = ax + b

重回帰分析のモデルの式は以下のようになります。

y = a_1 x_1 + a_2 x_2 + \dots + a_n x_n + b

y: 目的変数（結果）
x: 説明変数（原因）
a: 偏回帰係数
b: 切片

単回帰分析では a は回帰係数でしたが、重回帰分析では a は偏回帰係数になります。
他の変数の影響を取り除いた上で、特定の変数が目的変数にどれだけ影響を与えるかを示すため、「偏」の意味が追加されています。

重回帰分析を行ってみる

それでは、実際に重回帰分析を行ってみたいと思います。
前回の単回帰分析と同様に目的変数「収入」に対して、その他の変数の影響を分析してみたいと思います。

使用したデータ

前回の単回帰分析で使用したデータを使います

使用したデータ

データは適当に作ったものです

名前	年齢	収入	消費スコア	運動時間	支出	睡眠時間	体重
名前1	58	200000.0	58	1.0	184835.70765056164	4.602870175861717	95.64816793878958
名前2	48	216326.5306122449	86	1.183673469387755	166148.00943123671	6.032795106962874	93.31146809222858
名前3	34	232653.0612244898	82	1.3673469387755102	218506.87588462647	6.783251227163527	91.80942130551054
名前4	62	248979.5918367347	91	1.5510204081632653	275335.166289789	7.433435219254879	93.46825053686541
名前5	27	265306.1224489796	93	1.7346938775510203	200537.22922301688	5.303835620807539	93.3885296572368
名前6	40	281632.6530612245	73	1.9183673469387754	1240100.493497031	4.880964190262193	92.2707235035385
名前7	58	297959.1836734694	64	2.1020408163265305	317327.9877141451	6.844598129752072	87.81136087192208
名前8	38	314285.7142857143	81	2.2857142857142856	289800.3078862169	7.238004184558862	124.34261832042647
名前9	42	330612.2448979592	81	2.4693877551020407	241016.07662161972	11.977522198547547	88.31558808729692
名前10	30	346938.7755102041	73	2.6530612244897958	304679.0225874615	4.384706204365683	88.68578413179574
名前11	30	363265.306122449	90	2.836734693877551	83074.00471561836	7.762093057958416	84.85797805492166
名前12	43	379591.83673469385	98	3.0204081632653064	280386.9817092422	5.590288084350089	84.52664123034583
名前13	55	395918.3673469388	98	3.2040816326530615	328832.80745585274	6.07100540210992	34.67157801327479
名前14	59	412244.89795918367	61	3.3877551020408165	234131.9061344571	7.350840423629312	80.66881124163457
名前15	43	428571.4285714286	88	3.5714285714285716	256611.25123149127	6.702760468157123	83.76790878764554
名前16	22	444897.9591836735	51	3.7551020408163267	327803.9908848902	2.0361507272310417	83.93696985306002
名前17	41	461224.48979591834	52	3.938775510204082	318338.0358200135	4.836286482950855	80.16210220581893
名前18	21	477551.02040816325	98	4.122448979591837	397753.18295629433	6.165791895310264	81.39482089782486
名前19	43	493877.55102040817	86	4.3061224489795915	349700.837040266	6.783137597380328	79.19265980519732
名前20	63	510204.0816326531	98	4.4897959183673475	337548.0802393579	4.914200087189199	76.260780898953
名前21	49	526530.612244898	66	4.673469387755102	494506.9282419961	4.699819708383744	77.35544427224131
名前22	57	542857.1428571428	98	4.857142857142858	422996.89926138753	7.928673373317743	78.79035884721765
名前23	21	559183.6734693877	51	5.040816326530613	450723.34900990635	6.066543565084057	74.72426628912703
名前24	40	575510.2040816327	51	5.224489795918368	389170.7539546333	5.043316699321636	77.00683833203618
名前25	52	591836.7346938776	77	5.408163265306123	446250.251528843	7.985014799031697	67.7196934652899
名前26	31	608163.2653061225	72	5.591836734693878	492076.7417303913	7.8616774051551745	73.68462133528105
名前27	41	624489.7959183673	86	5.775510204081633	442042.15786357876	6.23317381442839	71.29654311606818
名前28	63	640816.3265306123	81	5.959183673469388	531437.9621417734	7.530545372757359	69.60606693172133
名前29	44	657142.8571428572	82	6.142857142857143	495682.3512183456	4.7548284333655175	69.46923583878528
名前30	68	673469.387755102	50	6.326530612244898	524190.8227144178	5.115485410368727	64.39220910957373
名前31	46	689795.918367347	68	6.510204081632653	521751.40408240777	6.801431319891085	67.0096358161617
名前32	61	706122.4489795918	51	6.6938775510204085	657511.8684091204	7.386644568953224	67.24483738792145
名前33	47	722448.9795918367	93	6.877551020408164	577284.3224365726	7.42529716751237	68.56803298744222
名前34	35	738775.5102040817	75	7.061224489795919	538134.8617154703	5.61803250848876	63.65733711447311
名前35	34	755102.0408163265	81	7.244897959183674	645208.8782582206	7.551080395043839	62.15852299829526
名前36	66	771428.5714285715	55	7.428571428571429	556100.6746443061	7.4037137950700505	61.85362876997378
名前37	63	787755.1020408163	81	7.612244897959184	640647.2613828909	7.742539976883791	63.769579745608226
名前38	22	804081.6326530612	53	7.795918367346939	545281.7999284603	7.141362604455774	61.67791038258467
名前39	56	820408.1632653062	60	7.979591836734694	589917.2281673234	6.675953018856914	59.04252040879245
名前40	26	836734.693877551	66	8.16326530612245	679230.816895497	6.322746485745819	60.21020833561447
名前41	40	853061.224489796	87	8.346938775510203	719372.3085916074	5.489131066246973	58.45946122114506
名前42	28	869387.7551020408	73	8.53061224489796	704078.6181411312	7.760533769831113	59.284228756575985
名前43	58	885714.2857142857	54	8.714285714285715	702789.0144520166	7.894655347021269	55.02446524081672
名前44	37	902040.8163265307	83	8.89795918367347	706577.4682817602	5.135683898949862	54.85487978843712
名前45	23	918367.3469387755	55	9.081632653061225	660767.7780326491	5.221455441377573	53.80762042842956
名前46	44	934693.8775510205	71	9.26530612244898	711762.891621081	5.942455014344906	50.74643949149087
名前47	33	951020.4081632653	60	9.448979591836736	737784.387982623	5.79369657194499	53.34734259494548
名前48	69	967346.9387755102	97	9.63265306122449	826733.662331354	7.977829850443283	52.35884523823733
名前49	28	983673.4693877551	65	9.816326530612246	804119.6899886272	4.7037010107093815	50.9285942602237
名前50	45	1000000.0	82	10.0	711847.9922318633	4.0723014544620835	49.530825733249706

データの各項目名です。
1.名前
2.年齢
3.収入
4.消費スコア
5.運動時間
6.支出
7.睡眠時間
8.体重

前準備

グラフに日本語ラベルを表示できるように japanize-matplotlib をインストールします。

!pip install -q japanize-matplotlib

必要のライブラリをインポートして、使用するデータを読み込んでおきます。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
plt.style.use('seaboran')　#グラフのスタイル 他にも bmh, ggplot, などいろいろある　
plt.rcParams['font.family'] = 'IPAexGothic' #日本語フォント

np.random.seed(0) # 裏で動く乱数の固定（乱数を固定しないと毎回、結果が異なってしまうため固定する）

# 分析を行うライブラリ
import statsmodels.api as sm
# 説明変数のスケーリングに使用するクラス
from sklearn.preprocessing import StandardScaler

df = pd.read_csv('/content/drive/MyDrive/correlation_analysis_testdata.csv')
df.head(3)

説明変数のスケーリング

異なるスケール（最小値から最大値までの幅）の説明変数がある場合、スケールが大きいものは偏回帰係数は小さくなってしまい、スケールの小さい偏回帰係数は大きくなってしまい、解析が難しくなってしまいます。
そこで、スケールを統一することで、すべての説明変数が同じスケールになり、解析がしやすくなります。

スケーリングの最も一般的な方法は次の2つになります

標準化（Standardization）: 平均を0、標準偏差を1にする方法
正規化（Normalization）: 値を0から1の範囲にスケーリングする方法

今回は標準化でスケーリングしてみます。

まずはデータを確認してみます

df.head(3)

説明変数を作成します。
データフレームから文字列項目の「名前」と目的変数「収入」を取り除いたものが、今回の説明変数になります。
元のデータフレームから dropメソッドで名前と収入を削除しています。
axis=1は列方向の削除です。

x = df.drop(['名前', '収入'], axis=1)

# 必要な項目だけを取り出してもOKです
# x = df[['年齢','収入','消費スコア','運動時間','支出','睡眠時間','体重']]

x.head(3)

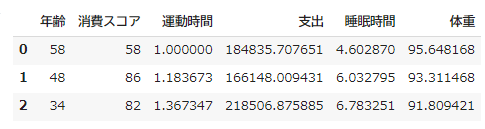
説明変数の標準化を行います。
標準化は sklearn（サーキットラーン）ライブラリのStandardScalerクラスのfit_transformメソッドを使用します。

# sklearnライブラリをインポート
from sklearn.preprocessing import StandardScaler
# StandardScalerクラスをインスタンス化
scaler = StandardScaler()
# 標準化
x_std = scaler.fit_transform(x)
x_std

標準化後はpandasのDataFrame型からnumpyのndarray型になります

type(x_std)

ndarray型だと見づらいのでpandasのDataFrame型に変換して値を確認してみます

colnms =x.columns
df_x_std = pd.DataFrame(x_std, columns=colnms)
df_x_std.head()

重回帰分析を行う

あとは前回の単回帰分析と同様の手順になります。
add_constant メソッドを使用して x（説明変数）に切片をセットする列を用意します。

import statsmodels.api as sm

x_std_with_const = sm.add_constant(df_x_std)
x_std_with_const

目的変数を作成します。

y  = df['収入']

OLSクラスをインスタンス化してfitメソッドで分析を行い、summary()メソッドで結果を表示します。

# 分析に使用するOLSクラスをインスタンス化
model = sm.OLS(y, x_std_with_const)

# 分析
res = model.fit()
 
# 結果を表示
res.summary()

結果の解釈の前にここまでのコードをまとめて表示します。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
import statsmodels.api as sm
from sklearn.preprocessing import StandardScaler

np.random.seed(0) # 裏で動く乱数の固定（乱数を固定しないと毎回、結果が異なってしまうため固定する）

plt.style.use('seaborn')
plt.rcParams['font.family'] = 'IPAexGothic'

# データ読込
df = pd.read_csv('/content/drive/MyDrive/correlation_analysis_testdata.csv');

# 目的変数
y  = df['収入']
# 説明変数
x = df.drop(['名前', '収入'], axis=1)
# StandardScalerクラスをインスタ化し説明変数を標準化
scaler = StandardScaler()
x_std = scaler.fit_transform(x)
# 説明変数に切片を追加
x_std_with_const = sm.add_constant(x_std)
# 分析に使用するOLSクラスをインスタンス化
model = sm.OLS(y, x_std_with_const)
# 分析
res = model.fit()
# 結果を表示
res.summary()

結果の解釈

自由度決定係数を確認

自由度決定係数（Adj. R_squared)でモデルの精度を確認します。

res.rsquared_adj

自由度決定係数が1に近いほどモデルの適合度が高いことになります。
サンプルサイズが小さいので 1 になってしまったかもしれません・・・

偏回帰係数を確認

偏回帰係数は目的変数に与える影響の強さを表します。
正の偏回帰係数：その変数が増加すると、目的変数も増加します
負の偏回帰係数：その変数が増加すると、目的変数も減少します
偏回帰係数の絶対値が大きいほど、目的変数への影響も大きいことを意味します。
また、標準化を行った後の偏回帰係数は、標準偏回帰係数と呼びます。

res.params

constは切片です。
x1:年齢
x2:消費スコア
x3:運動時間
x4:支出
x5:睡眠時間
x6:体重

P値を確認

ここでの帰無仮説と対立仮説は以下のようになります。
帰無仮説：a = 0 （影響はない）
対立仮説：a ≠ 0（何かしらの影響がある）

res.pvalues

どの結果も有意水準の0.05を下回っているので、どの説明変数も目的変数の収入に対して何かしらの影響があると判断できます

t値を確認

t値は説明変数の目的変数への影響度合いを表します。
t値が大きいほど目的変数に影響を与えているということになります

res.tvalues

x3の値が最も大きいので、運動時間が収入に最も影響を与えていると判断できます

偏回帰係数、p値、ｔ値をまとめて一覧表示する

偏回帰係数、p値、ｔ値を DataFrame にセットして、比較しやすいようにしてみます
index で行ラベルを指定します。

df_res = pd.DataFrame([res.params, res.pvalues, res.tvalues], index=['標準偏回帰係数', 'P値', 't値'])
df_res

.T属性で転置（行と列を入れ替え）します

pd.DataFrame([res.params, res.pvalues, res.tvalues], index=['偏回帰係数','P値','t値']).T

1行めのconst（切片）は不要なので除きます

df_res = pd.DataFrame([res.params[1:], res.pvalues[1:], res.tvalues[1:]], index=['標準偏回帰係数', 'P値', 't値']).T
df_res

t値の絶対値も追加しておきます

df_res['t値abs'] = abs(df_res['t値'])
df_res

p値が0.05以下（目的変数と何かしらの影響がある）データを、t値の絶対値の大きい順に並べ替えて表示します。

df_res[df_res['P値'] < 0.05].sort_values('t値abs', ascending=False)

目的変数「収入」に対して、運動時間と消費スコアが影響しているようです。

おわり

以上、重回帰分析の基本的なまとめでした。

重回帰分析とは

重回帰分析を行ってみる

使用したデータ

前準備

説明変数のスケーリング

重回帰分析を行う

結果の解釈

自由度決定係数を確認

偏回帰係数を確認

P値を確認

t値を確認

偏回帰係数、p値、ｔ値 を まとめて一覧表示する

おわり

Discussion

偏回帰係数、p値、ｔ値をまとめて一覧表示する