データ分析 python 単回帰分析
今回は単変量解析の単回帰分析について簡単にまとめてみます。
python + google colaboratory で 実行しています。
-
単変量解析
- 相関分析・・・2つの変数が一緒にどのように変化するかを調べる方法
- 単回帰分析・・・1つの独立変数と1つの従属変数を調べる方法
-
多変量解析
- 重回帰分析・・・複数の独立変数と1つの従属変数を調べる方法
単回帰分析とは
単回帰分析とは、1つの説明変数(独立変数)と1つの目的変数(従属変数)の間の関係をモデル化し、その関係を数式で表現する手法です。
主に、説明変数(x)が目的変数(y)にどのように影響を与えるかを分析します。
つまり、1つの原因(説明変数)が1つの結果(目的変数)に対して、どのような因果関係にあるかを明らかにするための手法です。
単回帰分析の目的は、2つの変数の関係を直線(回帰直線)で表現することです。
回帰直線は、次のような数式で表されます。
y: 目的変数(従属変数)
x: 説明変数(独立変数)
a: 回帰係数(説明変数Xが1単位変化する際の、目的変数Yの変化量)
b: 切片(YがXに影響されない場合のYの値)
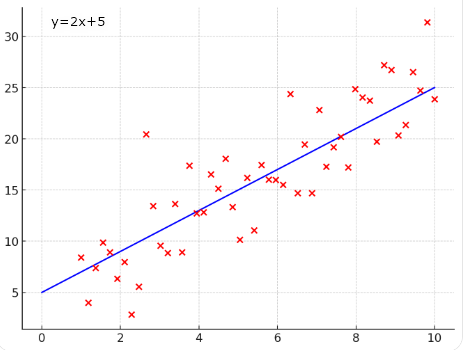
2つの変数の関係を直線(回帰直線)で表現することにより、点のない部分の値を予測できるようになります。
単回帰分析を行ってみる
それでは、実際に単回帰分析を行ってみたいと思います。
使用したデータ
使用したデータ
データは適当に作ったものです
| 名前 | 年齢 | 収入 | 消費スコア | 運動時間 | 支出 | 睡眠時間 | 体重 |
|---|---|---|---|---|---|---|---|
| 名前1 | 58 | 200000.0 | 58 | 1.0 | 184835.70765056164 | 4.602870175861717 | 95.64816793878958 |
| 名前2 | 48 | 216326.5306122449 | 86 | 1.183673469387755 | 166148.00943123671 | 6.032795106962874 | 93.31146809222858 |
| 名前3 | 34 | 232653.0612244898 | 82 | 1.3673469387755102 | 218506.87588462647 | 6.783251227163527 | 91.80942130551054 |
| 名前4 | 62 | 248979.5918367347 | 91 | 1.5510204081632653 | 275335.166289789 | 7.433435219254879 | 93.46825053686541 |
| 名前5 | 27 | 265306.1224489796 | 93 | 1.7346938775510203 | 200537.22922301688 | 5.303835620807539 | 93.3885296572368 |
| 名前6 | 40 | 281632.6530612245 | 73 | 1.9183673469387754 | 1240100.493497031 | 4.880964190262193 | 92.2707235035385 |
| 名前7 | 58 | 297959.1836734694 | 64 | 2.1020408163265305 | 317327.9877141451 | 6.844598129752072 | 87.81136087192208 |
| 名前8 | 38 | 314285.7142857143 | 81 | 2.2857142857142856 | 289800.3078862169 | 7.238004184558862 | 124.34261832042647 |
| 名前9 | 42 | 330612.2448979592 | 81 | 2.4693877551020407 | 241016.07662161972 | 11.977522198547547 | 88.31558808729692 |
| 名前10 | 30 | 346938.7755102041 | 73 | 2.6530612244897958 | 304679.0225874615 | 4.384706204365683 | 88.68578413179574 |
| 名前11 | 30 | 363265.306122449 | 90 | 2.836734693877551 | 83074.00471561836 | 7.762093057958416 | 84.85797805492166 |
| 名前12 | 43 | 379591.83673469385 | 98 | 3.0204081632653064 | 280386.9817092422 | 5.590288084350089 | 84.52664123034583 |
| 名前13 | 55 | 395918.3673469388 | 98 | 3.2040816326530615 | 328832.80745585274 | 6.07100540210992 | 34.67157801327479 |
| 名前14 | 59 | 412244.89795918367 | 61 | 3.3877551020408165 | 234131.9061344571 | 7.350840423629312 | 80.66881124163457 |
| 名前15 | 43 | 428571.4285714286 | 88 | 3.5714285714285716 | 256611.25123149127 | 6.702760468157123 | 83.76790878764554 |
| 名前16 | 22 | 444897.9591836735 | 51 | 3.7551020408163267 | 327803.9908848902 | 2.0361507272310417 | 83.93696985306002 |
| 名前17 | 41 | 461224.48979591834 | 52 | 3.938775510204082 | 318338.0358200135 | 4.836286482950855 | 80.16210220581893 |
| 名前18 | 21 | 477551.02040816325 | 98 | 4.122448979591837 | 397753.18295629433 | 6.165791895310264 | 81.39482089782486 |
| 名前19 | 43 | 493877.55102040817 | 86 | 4.3061224489795915 | 349700.837040266 | 6.783137597380328 | 79.19265980519732 |
| 名前20 | 63 | 510204.0816326531 | 98 | 4.4897959183673475 | 337548.0802393579 | 4.914200087189199 | 76.260780898953 |
| 名前21 | 49 | 526530.612244898 | 66 | 4.673469387755102 | 494506.9282419961 | 4.699819708383744 | 77.35544427224131 |
| 名前22 | 57 | 542857.1428571428 | 98 | 4.857142857142858 | 422996.89926138753 | 7.928673373317743 | 78.79035884721765 |
| 名前23 | 21 | 559183.6734693877 | 51 | 5.040816326530613 | 450723.34900990635 | 6.066543565084057 | 74.72426628912703 |
| 名前24 | 40 | 575510.2040816327 | 51 | 5.224489795918368 | 389170.7539546333 | 5.043316699321636 | 77.00683833203618 |
| 名前25 | 52 | 591836.7346938776 | 77 | 5.408163265306123 | 446250.251528843 | 7.985014799031697 | 67.7196934652899 |
| 名前26 | 31 | 608163.2653061225 | 72 | 5.591836734693878 | 492076.7417303913 | 7.8616774051551745 | 73.68462133528105 |
| 名前27 | 41 | 624489.7959183673 | 86 | 5.775510204081633 | 442042.15786357876 | 6.23317381442839 | 71.29654311606818 |
| 名前28 | 63 | 640816.3265306123 | 81 | 5.959183673469388 | 531437.9621417734 | 7.530545372757359 | 69.60606693172133 |
| 名前29 | 44 | 657142.8571428572 | 82 | 6.142857142857143 | 495682.3512183456 | 4.7548284333655175 | 69.46923583878528 |
| 名前30 | 68 | 673469.387755102 | 50 | 6.326530612244898 | 524190.8227144178 | 5.115485410368727 | 64.39220910957373 |
| 名前31 | 46 | 689795.918367347 | 68 | 6.510204081632653 | 521751.40408240777 | 6.801431319891085 | 67.0096358161617 |
| 名前32 | 61 | 706122.4489795918 | 51 | 6.6938775510204085 | 657511.8684091204 | 7.386644568953224 | 67.24483738792145 |
| 名前33 | 47 | 722448.9795918367 | 93 | 6.877551020408164 | 577284.3224365726 | 7.42529716751237 | 68.56803298744222 |
| 名前34 | 35 | 738775.5102040817 | 75 | 7.061224489795919 | 538134.8617154703 | 5.61803250848876 | 63.65733711447311 |
| 名前35 | 34 | 755102.0408163265 | 81 | 7.244897959183674 | 645208.8782582206 | 7.551080395043839 | 62.15852299829526 |
| 名前36 | 66 | 771428.5714285715 | 55 | 7.428571428571429 | 556100.6746443061 | 7.4037137950700505 | 61.85362876997378 |
| 名前37 | 63 | 787755.1020408163 | 81 | 7.612244897959184 | 640647.2613828909 | 7.742539976883791 | 63.769579745608226 |
| 名前38 | 22 | 804081.6326530612 | 53 | 7.795918367346939 | 545281.7999284603 | 7.141362604455774 | 61.67791038258467 |
| 名前39 | 56 | 820408.1632653062 | 60 | 7.979591836734694 | 589917.2281673234 | 6.675953018856914 | 59.04252040879245 |
| 名前40 | 26 | 836734.693877551 | 66 | 8.16326530612245 | 679230.816895497 | 6.322746485745819 | 60.21020833561447 |
| 名前41 | 40 | 853061.224489796 | 87 | 8.346938775510203 | 719372.3085916074 | 5.489131066246973 | 58.45946122114506 |
| 名前42 | 28 | 869387.7551020408 | 73 | 8.53061224489796 | 704078.6181411312 | 7.760533769831113 | 59.284228756575985 |
| 名前43 | 58 | 885714.2857142857 | 54 | 8.714285714285715 | 702789.0144520166 | 7.894655347021269 | 55.02446524081672 |
| 名前44 | 37 | 902040.8163265307 | 83 | 8.89795918367347 | 706577.4682817602 | 5.135683898949862 | 54.85487978843712 |
| 名前45 | 23 | 918367.3469387755 | 55 | 9.081632653061225 | 660767.7780326491 | 5.221455441377573 | 53.80762042842956 |
| 名前46 | 44 | 934693.8775510205 | 71 | 9.26530612244898 | 711762.891621081 | 5.942455014344906 | 50.74643949149087 |
| 名前47 | 33 | 951020.4081632653 | 60 | 9.448979591836736 | 737784.387982623 | 5.79369657194499 | 53.34734259494548 |
| 名前48 | 69 | 967346.9387755102 | 97 | 9.63265306122449 | 826733.662331354 | 7.977829850443283 | 52.35884523823733 |
| 名前49 | 28 | 983673.4693877551 | 65 | 9.816326530612246 | 804119.6899886272 | 4.7037010107093815 | 50.9285942602237 |
| 名前50 | 45 | 1000000.0 | 82 | 10.0 | 711847.9922318633 | 4.0723014544620835 | 49.530825733249706 |
データの各項目名です。
1.名前
2.年齢
3.収入
4.消費スコア
5.運動時間
6.支出
7.睡眠時間
8.体重
前準備
グラフに日本語ラベルを表示できるように japanize-matplotlib をインストールします。
!pip install -q japanize-matplotlib
必要のライブラリをインポートして、使用するデータを読み込んでおきます。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
np.random.seed(0) # 裏で動く乱数の固定(乱数を固定しないと毎回、結果が異なってしまうため固定する)
plt.style.use('seaboran') #グラフのスタイル 他にも bmh, ggplot, などいろいろある
plt.rcParams['font.family'] = 'IPAexGothic' #日本語フォント
import statsmodels.api as sm
df = pd.read_csv('/content/drive/MyDrive/correlation_analysis_testdata.csv')
df.head(3)

相関関係を確認する
相関関係をまとめて可視化する
seaborn の pairplot を使用すると、複数の変数をまとめて散布図を作成してくれます。
対角線上には各変数の分布も表示してくれます。
sns.pairplot(df)
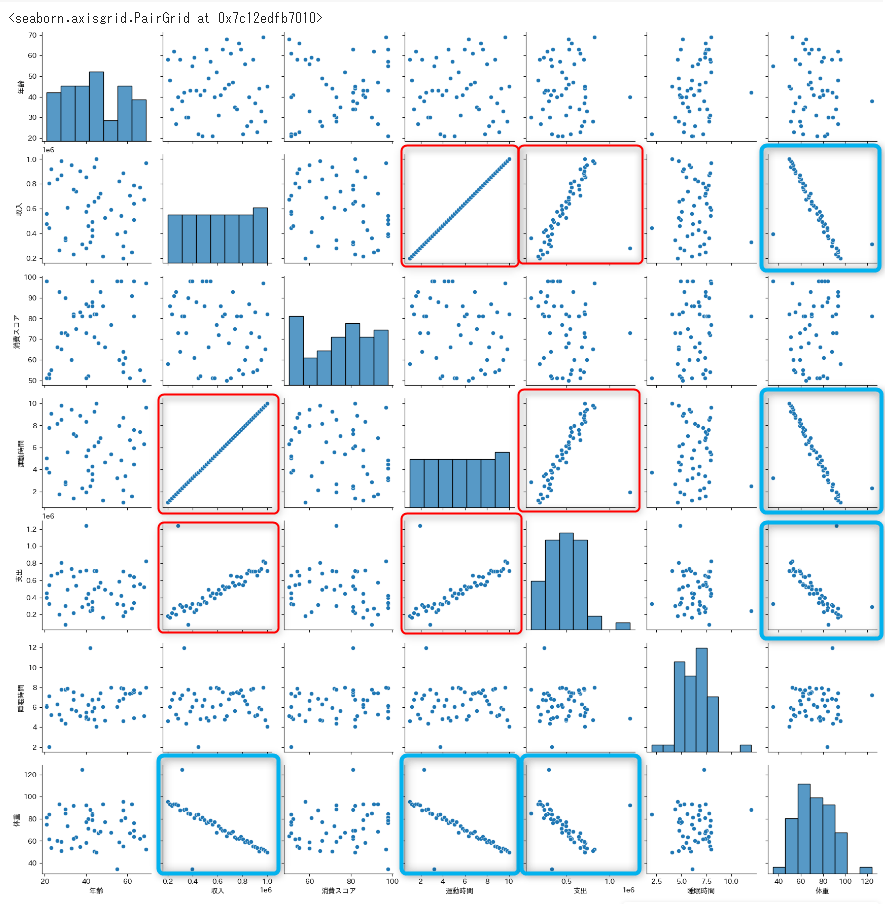
散布図の赤枠は正の相関関係が、青枠には負の相関関係があるようです。
- 正の相関
- 収入が多くなると、運動時間も多くなる
- 収入が多くなると、支出も多くなる
- 運動時間が多くなると、支出が多くなる
- 負の相関
- 収入が多くなると、体重が少なる
- 運動時間が多くなると、体重が少なくなる
- 支出が多くなると、体重が少なくなる
まとめて相関係数を確認する
df.corr(numeric_only=True)
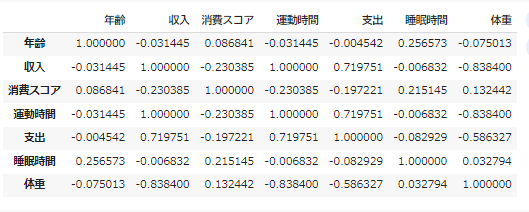
この表では相関係数が分かりにくいので、ヒートマップで表示してみます。
ヒートマップは seaborn の heatmap メソッドで表示します。
各パラメータの意味は下記のとおりです。
annot=True は各セルに数値を表示し、fmt='.2f' で小数点以下2桁にフォーマットしています。
vmax=1 と vmin=-1 で、カラースケールの最大値と最小値を指定しています。
square=True は各セルを正方形にします。
center=0 を指定することで、相関が 0 の部分がカラーバーの中心になり、プラスの相関(正の数値)とマイナスの相関(負の数値)をそれぞれ異なる色で強調することができます。
sns.heatmap(df.corr(numeric_only=True), annot=True, square=True, vmax=1, vmin=-1, center=0, fmt='.2f');
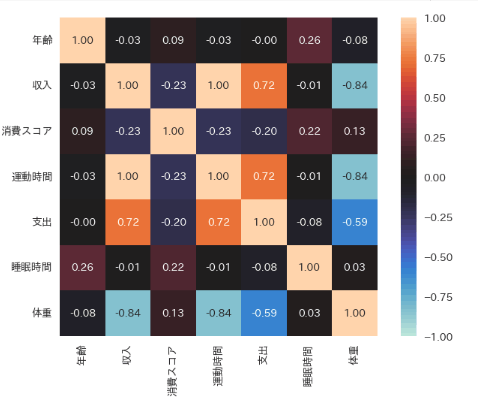
体重と収入の相関係数が -0.84 と強い負の相関があります。
「体重」を原因としたときに、結果の「収入」にどれぐらい影響を与えているのか因果関係をを分析してみたいと思います。
単回帰分析の実装
statsmodelライブラリには単回帰分析を行うためのクラスがいくつか用意されいています。
- 最小二乗法 (OLS: Ordinary Least Squares):最も基本的な最小二乗法。等分散性と独立な誤差項を仮定。
- 加重最小二乗法 (WLS: Weighted Least Squares):異分散性がある場合に重みを考慮して回帰を行う。
- 一般化最小二乗法 (GLS: Generalized Least Squares): 説明変数の相関や誤差項の自己相関を考慮する。
- 再帰的最小二乗法 (Recursive LS): 動的なデータや逐次的なデータに対して、データが追加されるたびにモデルを更新。
今回は statsmodels ライブラリ から 最も基本的な OLS クラスを使って単回帰分析を行ってみたいと思います。
ライブラリをインポートします
import statsmodels.api as sm
説明変数と目的変数を用意します
# 目的変数
y = df['収入']
# 説明変数
x = df['体重']
ここで x のデータを見てみます
x.head(3)
| 体重 | |
|---|---|
| 0 | 95.648168 |
| 1 | 93.311468 |
| 2 | 91.809421 |
| 3 | 93.468251 |
| 4 | 93.388530 |
add_constant メソッドを使用して x(説明変数)に切片をセットする列を用意します。
x_adconst = sm.add_constant(x)
x_adconst.head(5)
| index | const | 体重 |
|---|---|---|
| 0 | 1.0 | 95.64816793878958 |
| 1 | 1.0 | 93.31146809222858 |
| 2 | 1.0 | 91.80942130551054 |
| 3 | 1.0 | 93.4682505368654 |
| 4 | 1.0 | 93.3885296572368 |
切片をセットする列(const)が追加されました。切片の初期値は1がセットされています。
説明変数と、目的変数をパラメータにセットしてOLSクラスをインスタンス化します。
ols = sm.OLS(y, x_adconst)
fit メソッドで分析を行います
res = ols.fit()
分析の結果を summary メソッドを使って表示します
res.summary()
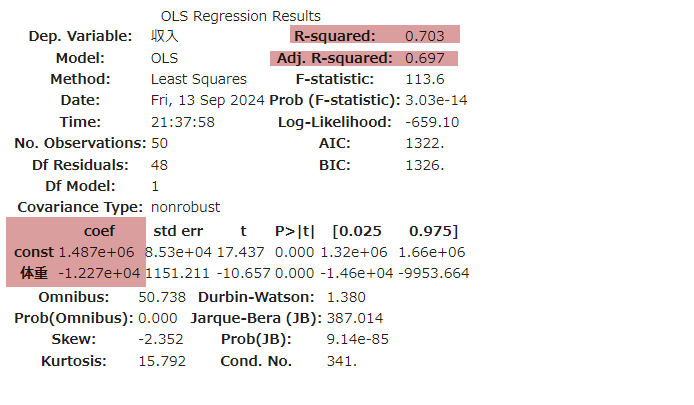
1. R-squared (決定係数)
- R-squared は、モデルが目標値(実際のデータ)に対して予測値がどれくらい当てはまっているのか、つまりモデルの適合度を示す指標です。
- R-squared の値が1に近いほど、モデルの予測が目標値に近いことを意味します。
逆に、R-squared の値が0に近い場合は、モデルが目的変数の変動をほとんど説明できていないことを意味ます。
rsuqred プロパティでも参照することができます
res.rsquared

この値は、モデルが目的変数「収入」の変動の 70.3% を説明していることを示します。
つまり、説明変数「体重」に基づくモデルは、収入の70.3%の変動を説明できるということです。
2. Adj. R-squared (自由度調整み決定係数) アジャ アール スクイアード
- R-squaredは説明変数の数が増えるほど 1 に近づくという傾向があり、たとえその説明変数がモデルに有効でなくてもR-squared が高くなってしまう可能性があります。
- Adj. R-squared は 説明変数の数とデータのサンプル数に基づいて補正が加えられます。
- 単回帰分析の場合、説明変数は1つなのであまり気にしなくてもいいです。
3. coef (回帰係数) コーエフ
- const (切片): 1.487e+06
これは、体重がゼロのときの収入の予測値(切片)です。ここでは 1,487,000円 となります。 - 体重(回帰係数の値): -1.227e+04
体重が1kg増えるごとに、収入が 12,270円減少 することを示しています(回帰係数が負なので、逆の関係です)
params プロパティでも参照することができます
res.params
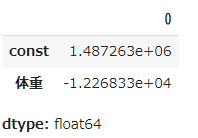
回帰係数が統計的に有為かを検定する
pvalues プロパティで回帰係数と切片のP値が確認できます
res.pvalues

- 帰無仮説:a(回帰係数)=0 説明変数と目的変数には関係性がない
- 対立仮説:a(回帰係数)≠0 説明変数と目的変数にはなんらんかの関係性がある
今回の 回帰係数のP値「2.095479e-2」 は 切片のP値は「3.028222e-14」と 有意水準の 0.05 より小さいので、帰無仮説を棄却し、何らかの関係性があるといえます
予測する
回帰分析では変数同士の関係性を直線の式で表現できるので、未知のデータに対して予測ができます。
今回は未知のデータの代わりに、先ほどまで使用していた既知のデータで予測を行ってみます。
先ほど分析した結果に対して、predict メソッドを使用すると、予測値を計算できます。
pred = res.predict()
pred[:5] # 最初から5つを表示

y(目的変数)である収入について予測した結果を3つ表示してみました。
実際のデータの最初の5つを表示してみます
df['収入'][:5]

この比較からモデルの予測値は、実際の収入よりも大きく予測されているようです。
回帰直線の可視化
実際のデータと回帰直線を同じグラフに描画してみます。
これによりモデルがどのようにデータにフィットしているかを視覚的に確認できます。
データ読込からグラフ化までのコードです。
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
import japanize_matplotlib
import pandas as pd
import seaborn as sns
np.random.seed(0) # 裏で動く乱数の固定(乱数を固定しないと毎回、結果が異なってしまうため固定する)
plt.style.use('seaborn')
plt.rcParams['font.family'] = 'IPAexGothic'
df = pd.read_csv('/content/drive/MyDrive/correlation_analysis_testdata.csv');
# 目的変数
y = df['収入']
# 説明変数
x = df['体重']
# 説明変数に切片追加
x_withconst = sm.add_constant(x)
# OLS モデルを作成し、フィッティング
model = sm.OLS(y, x_withconst)
result = model.fit()
# 結果を表示
print(result.summary())
# 予測値を計算
pred = result.predict()
# グラフを作成
fig, ax = plt.subplots()
# 実際のデータを散布図で表示
# 下記のどちらでもいい
# ax.plot(x, y, 'o', label='データ') # 折れ線グラフを描画するプロット。を'o'と指定して点だけをプロットしている
ax.scatter(x, y, label="Actual Data", color="blue") # 散布図のプロット
# 回帰直線を表示
ax.plot(x, pred, 'red', label='予測値')
# 凡例を「最適な場所」に配置
ax.legend(loc='best')
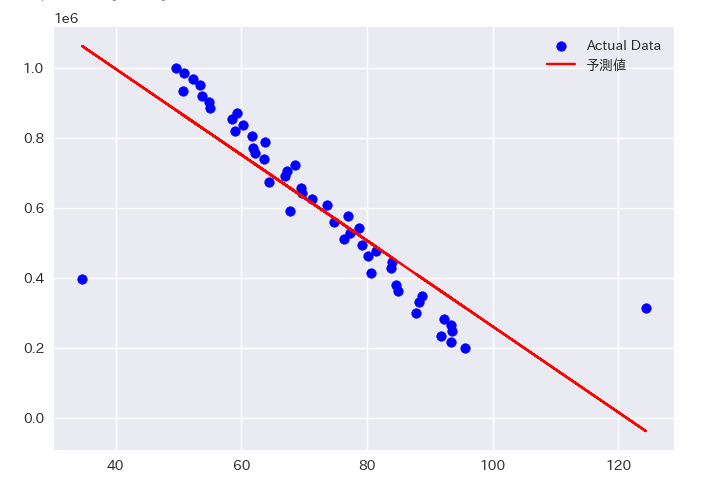
この可視化により、回帰モデルがどれだけ実際のデータに適合しているかを視覚的に確認できます。
特に、回帰直線がデータのトレンド(全体的な傾向や方向性)に沿っていれば、モデルがデータをうまく捉えていることを意味します。
おわり
以上、単回帰分析の基本的なまとめでした。
Discussion