データ分析 python 相関分析 & 無相関検定

今回は単変量解析の相関分析について簡単にまとめてみます。
python + google colaboratory で 実行しています。

• 単変量解析
  • 相関分析・・・2つの変数が一緒にどのように変化するかを調べる方法
  • 単回帰分析・・・1つの独立変数と1つの従属変数を調べる方法
• 多変量解析
  • 重回帰分析・・・複数の独立変数と1つの従属変数を調べる方法

相関分析とは

相関分析とは
2つの変数間にどのような関係があるかを調べる統計手法です。
主に2つの変数が一緒にどのように変化するか（正の相関、負の相関、または無相関）を測定します。
相関分析は、因果関係（一方の変数が原因で、もう一方の変数に直接影響する）を示すものではなく、あくまで「関係性」を確認する方法です。

相関分析では相関係数を算出します。
相関係数は -1 から 1 までの値をとります。
相関係数が 1 に近いほど強い正の相関となり、-1 に近いほど 強い負の相関となります。
相関係数が 0 に近いほど無相関になります。

正の相関

一方の変数が増加する際に、もう一方の変数も増加する場合。
1に近いほど強い正の相関。
例えば、勉強時間と成績が正の相関を持つことがある。

負の相関

一方の変数が増加すると、もう一方の変数が減少する場合。
-1に近いほど強い負の相関。
例えば、運動時間と体重が負の相関を持つことがある。

無相関

変数間に関係が見られない場合。0に近いほど関係がない。
相関の強さは 相関係数（通常 -1から1までの範囲）で表され、0に近いほど関係がないことを示します。

散布図

散布図とは、2つの数値データの関係を視覚的に表すためのグラフです。

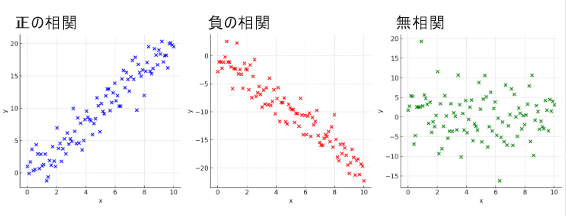
相関係数の目安

相関係数(r)に絶対的な基準は有りませんが、一般的な目安というものはあります。

• 相関係数 0.3未満（r < 0.3）・・・　ほぼ無相関
• 相関係数 0.3以上 0.5未満（0.3 ≦ r < 0.5）・・・弱い相関
• 相関係数 0.5以上 0.7未満（0.5 ≦ r < 0.7）・・・やや相関あり
• 相関係数 0.7以上 0.9未満（0.7 ≦ r < 0.9）・・・強い相関
• 相関係数 0.9以上（0.9 ≦ r）・・・非常に強い相関

相関分析を行ってみる

それでは、実際に相関分析を行ってみたいと思います。

使用したデータ

使用したデータ

データは適当に作ったものです

名前	年齢	収入	消費スコア	運動時間	支出	睡眠時間	体重
名前1	58	200000.0	58	1.0	184835.70765056164	4.602870175861717	95.64816793878958
名前2	48	216326.5306122449	86	1.183673469387755	166148.00943123671	6.032795106962874	93.31146809222858
名前3	34	232653.0612244898	82	1.3673469387755102	218506.87588462647	6.783251227163527	91.80942130551054
名前4	62	248979.5918367347	91	1.5510204081632653	275335.166289789	7.433435219254879	93.46825053686541
名前5	27	265306.1224489796	93	1.7346938775510203	200537.22922301688	5.303835620807539	93.3885296572368
名前6	40	281632.6530612245	73	1.9183673469387754	1240100.493497031	4.880964190262193	92.2707235035385
名前7	58	297959.1836734694	64	2.1020408163265305	317327.9877141451	6.844598129752072	87.81136087192208
名前8	38	314285.7142857143	81	2.2857142857142856	289800.3078862169	7.238004184558862	124.34261832042647
名前9	42	330612.2448979592	81	2.4693877551020407	241016.07662161972	11.977522198547547	88.31558808729692
名前10	30	346938.7755102041	73	2.6530612244897958	304679.0225874615	4.384706204365683	88.68578413179574
名前11	30	363265.306122449	90	2.836734693877551	83074.00471561836	7.762093057958416	84.85797805492166
名前12	43	379591.83673469385	98	3.0204081632653064	280386.9817092422	5.590288084350089	84.52664123034583
名前13	55	395918.3673469388	98	3.2040816326530615	328832.80745585274	6.07100540210992	34.67157801327479
名前14	59	412244.89795918367	61	3.3877551020408165	234131.9061344571	7.350840423629312	80.66881124163457
名前15	43	428571.4285714286	88	3.5714285714285716	256611.25123149127	6.702760468157123	83.76790878764554
名前16	22	444897.9591836735	51	3.7551020408163267	327803.9908848902	2.0361507272310417	83.93696985306002
名前17	41	461224.48979591834	52	3.938775510204082	318338.0358200135	4.836286482950855	80.16210220581893
名前18	21	477551.02040816325	98	4.122448979591837	397753.18295629433	6.165791895310264	81.39482089782486
名前19	43	493877.55102040817	86	4.3061224489795915	349700.837040266	6.783137597380328	79.19265980519732
名前20	63	510204.0816326531	98	4.4897959183673475	337548.0802393579	4.914200087189199	76.260780898953
名前21	49	526530.612244898	66	4.673469387755102	494506.9282419961	4.699819708383744	77.35544427224131
名前22	57	542857.1428571428	98	4.857142857142858	422996.89926138753	7.928673373317743	78.79035884721765
名前23	21	559183.6734693877	51	5.040816326530613	450723.34900990635	6.066543565084057	74.72426628912703
名前24	40	575510.2040816327	51	5.224489795918368	389170.7539546333	5.043316699321636	77.00683833203618
名前25	52	591836.7346938776	77	5.408163265306123	446250.251528843	7.985014799031697	67.7196934652899
名前26	31	608163.2653061225	72	5.591836734693878	492076.7417303913	7.8616774051551745	73.68462133528105
名前27	41	624489.7959183673	86	5.775510204081633	442042.15786357876	6.23317381442839	71.29654311606818
名前28	63	640816.3265306123	81	5.959183673469388	531437.9621417734	7.530545372757359	69.60606693172133
名前29	44	657142.8571428572	82	6.142857142857143	495682.3512183456	4.7548284333655175	69.46923583878528
名前30	68	673469.387755102	50	6.326530612244898	524190.8227144178	5.115485410368727	64.39220910957373
名前31	46	689795.918367347	68	6.510204081632653	521751.40408240777	6.801431319891085	67.0096358161617
名前32	61	706122.4489795918	51	6.6938775510204085	657511.8684091204	7.386644568953224	67.24483738792145
名前33	47	722448.9795918367	93	6.877551020408164	577284.3224365726	7.42529716751237	68.56803298744222
名前34	35	738775.5102040817	75	7.061224489795919	538134.8617154703	5.61803250848876	63.65733711447311
名前35	34	755102.0408163265	81	7.244897959183674	645208.8782582206	7.551080395043839	62.15852299829526
名前36	66	771428.5714285715	55	7.428571428571429	556100.6746443061	7.4037137950700505	61.85362876997378
名前37	63	787755.1020408163	81	7.612244897959184	640647.2613828909	7.742539976883791	63.769579745608226
名前38	22	804081.6326530612	53	7.795918367346939	545281.7999284603	7.141362604455774	61.67791038258467
名前39	56	820408.1632653062	60	7.979591836734694	589917.2281673234	6.675953018856914	59.04252040879245
名前40	26	836734.693877551	66	8.16326530612245	679230.816895497	6.322746485745819	60.21020833561447
名前41	40	853061.224489796	87	8.346938775510203	719372.3085916074	5.489131066246973	58.45946122114506
名前42	28	869387.7551020408	73	8.53061224489796	704078.6181411312	7.760533769831113	59.284228756575985
名前43	58	885714.2857142857	54	8.714285714285715	702789.0144520166	7.894655347021269	55.02446524081672
名前44	37	902040.8163265307	83	8.89795918367347	706577.4682817602	5.135683898949862	54.85487978843712
名前45	23	918367.3469387755	55	9.081632653061225	660767.7780326491	5.221455441377573	53.80762042842956
名前46	44	934693.8775510205	71	9.26530612244898	711762.891621081	5.942455014344906	50.74643949149087
名前47	33	951020.4081632653	60	9.448979591836736	737784.387982623	5.79369657194499	53.34734259494548
名前48	69	967346.9387755102	97	9.63265306122449	826733.662331354	7.977829850443283	52.35884523823733
名前49	28	983673.4693877551	65	9.816326530612246	804119.6899886272	4.7037010107093815	50.9285942602237
名前50	45	1000000.0	82	10.0	711847.9922318633	4.0723014544620835	49.530825733249706

データの各項目名です。
1.名前
2.年齢
3.収入
4.消費スコア
5.運動時間
6.支出
7.睡眠時間
8.体重

前準備

グラフに日本語ラベルを表示できるように japanize-matplotlib をインストールします。

!pip install -q japanize-matplotlib

必要のライブラリをインポートして、使用するデータを読み込んでおきます。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns

np.random.seed(0)　# 裏で動く乱数の固定（乱数を固定しないと毎回、結果が異なってしまうため固定する）

plt.style.use('seaboran')　#グラフのスタイル 他にも bmh, ggplot, などいろいろある　
plt.rcParams['font.family'] = 'IPAexGothic' #日本語フォント

from scipy import stats

df = pd.read_csv('/content/drive/MyDrive/correlation_analysis_testdata.csv')
df.head(3)

データの情報を確認しておきます

df.info()

サンプル数は50です。欠損値はありません。

データの統計量も確認しておきます

df.describe()

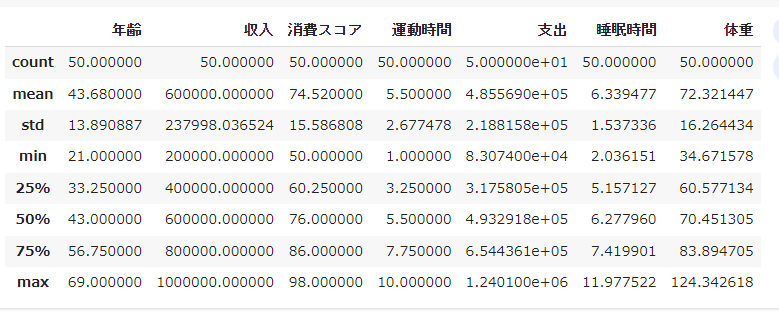
相関関係を可視化で確認

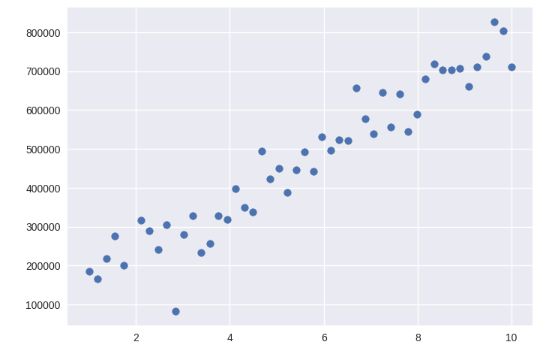
運動時間と支出の相関関係を散布図で確認してみます。
x軸を運動時間、y軸を支出とします。

plt.scatter(df['運動時間'], df['支出'])

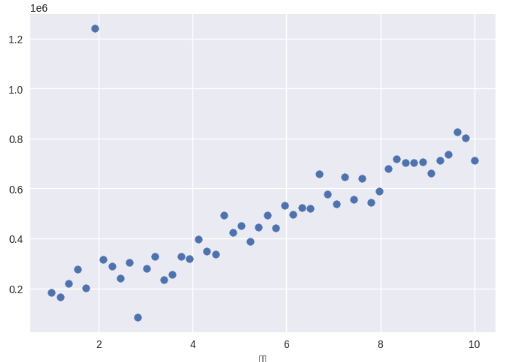
相関係数を確認する

相関係数は、2つの変数がどの程度関連しているかを示す指標で、-1から1の間の値を取ります。
相関係数はデータフレームの corr メソッドで確認できます。
corr は correlation（コリレーション）の略です

df_act_cost = df[['運動時間','支出']]
df_act_cost.corr()

index	運動時間	支出
運動時間	1.0	0.7197507709490326
支出	0.7197507709490326	1.0

相関係数が 0.71 ですので「強い相関」があることがわかりました。

外れ値を削除する

外れ値とはとは、他のデータ点から大きく外れているデータ点を指します。
左上の赤丸のデータです

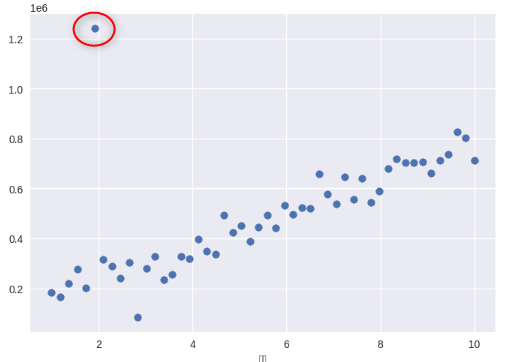
外れ値があると相関分析が正しく算出できないことがあるので、データから削除しておきます。
本来なら 四分位範囲（IQR）を使用して外れ値を検出し、dropを使って削除するのですが、また別の記事で紹介するとして、今回はデータから目視で見つけて削除します。

df_act_cost

散布図からみて、赤で囲んだデータが外れ値です。

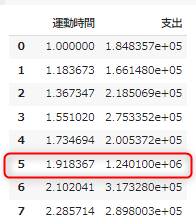
dropメソッドを指定して削除します

df_act_cost_clean = df_act_cost.drop(df_act_cost.index[(df_act_cost[ '運動時間'] <= 2) & (df_act_cost['支出'] > 1.240100e+06 )])

データフレームのサンプル数を確認してみます

len(df_act_cost_clean)
# → 49 と出力された

散布図でも確認しておきます。

それではもう一度、相関係数を確認してみます。

df_act_cost_clean.corr()

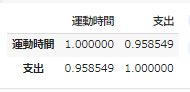
相関係数が 0.71 から 0.95 になりました。

運動時間が増えると、支出が増えるという相関関係があるようです。

まとめて可視化する

seaborn の pairplot を使用すると、複数の変数をまとめて散布図を作成してくれます。
対角線上には各変数の分布も表示してくれます。

sns.pairplot(df)

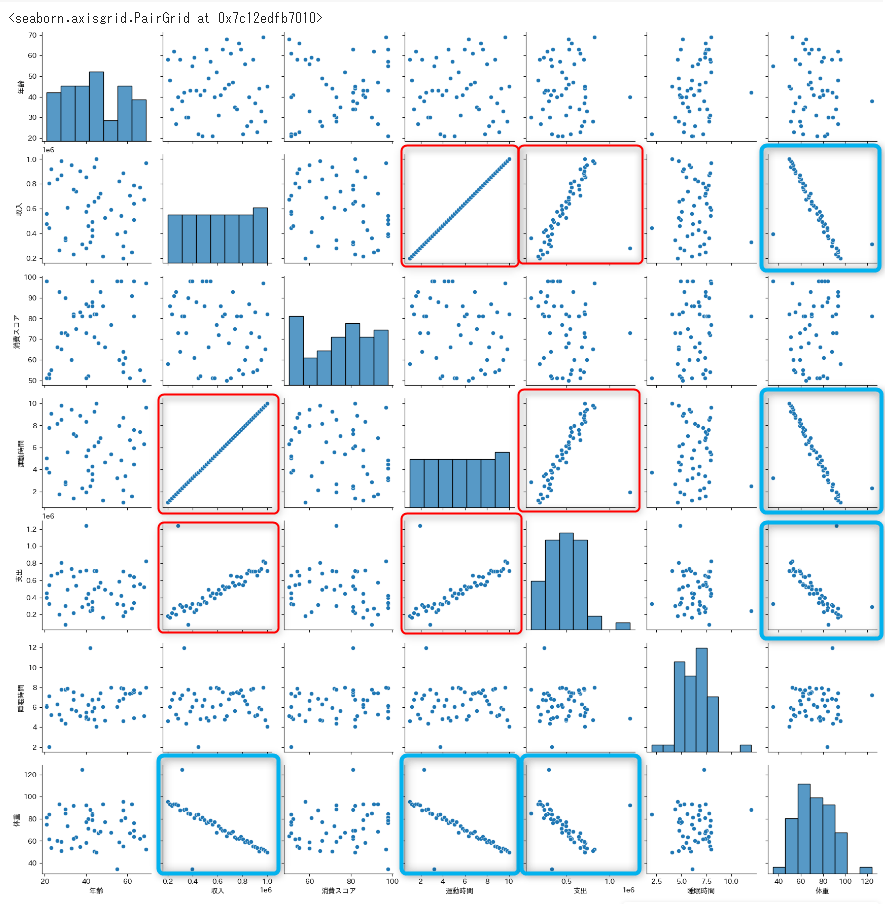
散布図の赤枠は正の相関関係が、青枠には負の相関関係があるようです。

• 正の相関
  • 収入が多くなると、運動時間も多くなる
  • 収入が多くなると、支出も多くなる
  • 運動時間が多くなると、支出が多くなる
• 負の相関
  • 収入が多くなると、体重が少なる
  • 運動時間が多くなると、体重が少なくなる
  • 支出が多くなると、体重が少なくなる

まとめて相関係数を確認する

df.corr(numeric_only=True)

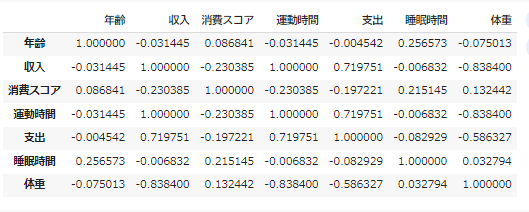
この表では相関係数が分かりにくいので、ヒートマップで表示してみます。
ヒートマップは seaborn の heatmap メソッドで表示します。
各パラメータの意味は下記のとおりです。
annot=True は各セルに数値を表示し、fmt='.2f' で小数点以下2桁にフォーマットしています。
vmax=1 と vmin=-1 で、カラースケールの最大値と最小値を指定しています。
square=True は各セルを正方形にします。
center=0 を指定することで、相関が 0 の部分がカラーバーの中心になり、プラスの相関（正の数値）とマイナスの相関（負の数値）をそれぞれ異なる色で強調することができます。

sns.heatmap(df.corr(numeric_only=True), annot=True, square=True, vmax=1, vmin=-1, center=0, fmt='.2f');

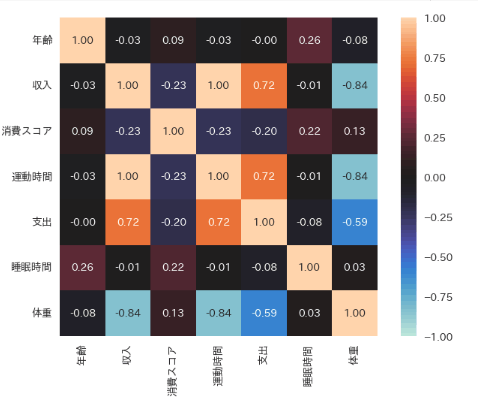
無相関検定

今回、算出した相関係数は標本集団の相関係数です。
母集団でも相関関係があるかはわかりません。
そこで母集団も同様に相関があるかどうかの検定を行います。
この検定を無相関検定と言います。

無相関検定とは、2つの変数の間に相関がない（無相関である）ことを検証するための統計的検定です。
相関係数が小さい（たとえば0.1）からといって、必ずしも2つの変数が「本当に無相関」であるとは言い切れません。そのため、相関係数だけでは不十分で、統計的に有意かどうかを判断するために無相関検定が必要です。

母集団でも相関があるか検定する

検定は scipy の pearsonr（ピアソンアール）メソッドで行います。

仮説

• 帰無仮説：母相関係数は0である（標本集団と同様の相関はない）
• 対立仮説：母相関係数は0でない（標本集団と同様の有意な相関がある）

有意水準

5%

検定

stats.pearsonr(df_act_cost_clean['運動時間'], df_act_cost_clean['支出'])

PearsonRResult(statistic=0.9585486792807425, pvalue=2.8431300363957587e-27)

判定

有意水準 0.05 > P値 2.84e-27
帰無仮説を棄却し、対立仮説を採用。
つまり母集団には標本集団と同様の有意な相関があるといえる

以上、相関分析および無相関検定の手順でした