SIMD下座!?HLACを楽々ベクトル化!
これまでのお話
アダコテックではHLACという特徴量を用いた異常検知モデルを提供し、これまで3回に渡って要素技術を解説してきました。
今回はちょっと毛色を変えて、私自身の興味があったHLACそのものに関する実装の話です!
関連としてはCTO紹介の下記の濃淡HLACを対象として
t-ibe先生の処理高速化まわりの記事に関連します。
CPUかGPUか
パソコンで計算をするという行為はかつてCPU(Central Processing Unit) の役割でしたが、GPGPU(General Purpose computing with Graphical Processing Unit) という概念の登場により、GPUも汎用計算部の一つとして扱うことが近年では一般的です。汎用計算部が2つもあるなど贅沢ですね?1つにしましょうか!

CPUだけの世界
NvidiaとAMDの社長が唐揚げにレモンを振りかけられたとして一方的にGPUの生産を止めた世界において、パソコンができることといえば
- WordやExcel、メールの送信といった書類作成系のアプリはほぼ問題なく動作
- Youtubeを見る、写真を加工するといったアプリは高解像度になるほど激重に
- 3DCGのゲームなどもってのほか (マイクラは影Modなしなら動作しそう)
という世界です。事務仕事は捗りそう?ただし美しいUIなどはなく、四角や丸といった簡単な図形であったり、あるいはフォントだけが表示されるような状態です。(nanoとかviの世界観)
自分のパソコンはGPU搭載してないけど普通に動いてるよ?と思う方もいるかも知れませんが、実は近年CPUには超小型のGPUが搭載されているため、こういった極端な世界にならずに済んでいるだけなのです。
GPUだけの世界
逆にIntelとAMDの社長が3時のおやつにきのこの山を出されたとして一方的にCPUの生産を止めた世界では下記の状態と思われます。
- 動画の再生だけであれば高解像度でも軽快に動作し、写真のレタッチはだいたいできる
- 3DCGで作られた美しいゲーム画面はあるものの、なにかの入力のたびにラグが発生する
- WordやExcelがすごくもっさり動作し、メールの送信に妙な時間がかかる
Youtube専用マシンにできるかもしれませんが、動画データのダウンロードにはかなり時間を要するかもしれません。Windowsが動いているなどとも思わないほうが良いでしょう。
コンピュータもアンサンブルモデル
なんとなく計算と言ってもCPUとGPUでは得意分野が異なることは感じていただけたと思います。
世界の比較に用いた例では下記の2区分の処理を比較しています。
-
A: 順番通りに処理を進める必要のあるタスク
- テキストの編集、メールの送信、入力の対応
-
B: 順番を気にせず大量に同じ処理を行うタスク
- 動画の再生(表示画面の更新)、画像へのフィルタ処理、3次元頂点の計算
もっと身近な例でいけば恋愛はAでナンパはBでsうゎぁなにおすr(
察しの良い読者の皆様におかれましてはもうお気づきと思いますが、CPUはAのような直列型の処理が得意で、GPUはBのような並列型の処理に特化した計算部です。
このような特性の違いからCPUとGPUの処理には棲み分けがあり、コンピュータを構成する上でこれもまた一つのアンサンブルといえます!
ではHLACはどこで処理すべきか? という話になりますが、画像ではボカシであったりエッジ強調であったりと、ピクセル全てに同じような処理を行うことが多く、画像処理分野においてGPUとの相性は抜群です! であれば、3x3ピクセル領域で同じ計算を行うHLACもまたGPUで処理を実装すれば早くなることは自明のように思いますが、これがそう簡単な話ではないのです。
Single Instruction Multiple Data: SIMD
SIMD(日本語読みはシムディーやシムドが多い)を初めて聞く方もご安心、SIMDは今やあらゆるソフトで利用されている機能です。SIMDとはCPU上においてベクトルを扱う仕組みで、CPUの弱点である並列型の処理をいい感じにします。 ベクトルと聞いて卒倒しそうな方もご安心、数学的なベクトルという概念ではなく、SIMDにおけるベクトルとはパケットのような小さなデータの集まりを意味し、単一のスカラとの対象性を持った言葉として使用されます。
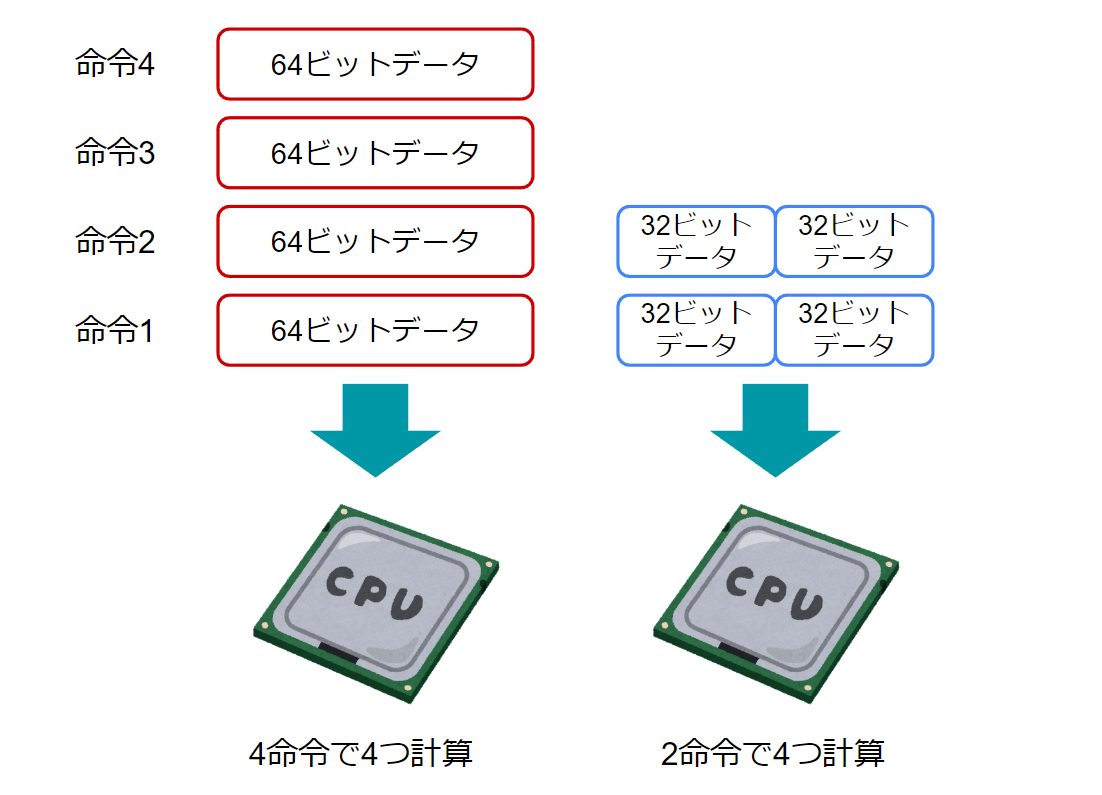
次の例でいくと一つ一つの変数はスカラであり、それらのひとまとまりはベクトルです。図にしてみるとちょっとかっこいいので4次元ベクトルと言いたくなってきません?

2010年前後には64ビットOSの普及開始に伴い、私のパソコンは64bit対応CPUなのか?という悩みで夜しか眠れない時期がありましたが、その話とSIMDも関係しています。かつては32bitのCPUが主流でしたが、この32や64という数値はざっくりと一度にCPUが処理できるビット量と理解いただければと思います。よって、画像処理における一般的な1ピクセルの値はだいたい256階調の8ビットデータであるので、64bitCPUは単純計算で最大で8ピクセル分の計算を一度に計算することができます。
かつては8つの計算に8つの命令が必要でしたが、これが1つの命令になるため、CPUからすれば1回の仕事で8倍の量をこなせるSIMD、どんどんキットカットのサイズが小さくなる現代では是非マスターしておきたい技術です。えっ…… プログラムの作り方ですか? そ、そうですね… 単純な計算処理の記述とはいえ、一度に複数の変数をまとめて扱うにはプログラム上で指示する必要があります。そしてそれは一般的な書式ではなく、拡張命令と呼ばれるスタイルで記述する必要があります。具体的にはIntelのCPUであれば次のリンクの命令セットのプログラミングリファレンスを読めばバッチリです!
…
……
全てで180ページ…… 😇
雰囲気を知りたい方はぜひt_ibe先生の記事をご確認ください!
Compute Unified Device Architecture: CUDA
ちょっとSIMDはそうめんに薬味を準備することを怠るような私のような人類には早すぎるかもしれません!ここはひとまずGPUの方の様子も見てみましょう!AMDのROCmなどもありますが、現在GPUでは主流プラットフォームである謎の半導体企業NVIDIAのCUDA(クーダ)について触れておこうと思います。
表題からしてSIMDと対をなすような書き方となっていますが、SIMDは具体的な処理手法であって、CUDAはプラットフォームです。 よってCUDAにおいてもSIMDの概念は存在し、GPUはまさにSIMDネイティブとも言うべきデバイスです。その源流はプログラマブルシェーダと呼ばれるGPUの機能になるのですが、プログラマブルシェーダが何たるかを理解したい方は小難しい話はともかく、下記のようなGLSLコードによって記述されるステキアートを見たほうがより興味が深まると思います。
次に例として最もシンプルなGLSLコードを示します。下記のコードでは画面座標ごとにピクセルの色を着色(青を0.5に固定して緑と赤の成分を座標に応じて変更) する処理を記述しています。そしてこの処理はすべての座標において並列で実行されます。
precision mediump float;
uniform vec2 resolution;
void main(void){
vec2 uv = gl_FragCoord.xy/resolution; // 画面座標を正規化し0~1の値域にする
gl_FragColor = vec4(uv.x, uv.y, 0.5, 1); // 画面座標ごとに着色
}
これを次のページに貼り付けてCtrl+sをすると実行されます。 実行すると下記のようになります
(Zennの画像圧縮でノイズが目立ちますが、実際はボロノイ図のようなノイズはないです)
コードを見るとわかるように、vecというGPU特有のベクトル型というデータがあり、1節前で見たSIMDのデータ構造そのままです。そうです、GPUのコードでは1つの座標ごとにデータがあると考え、座標ごとの処理を記述するだけで、それは自然とSIMDを考えた(考えざるを得ないとも言う)プログラムになります!
ようやく私のような床掃除をルンバ丸投げ人類にも理解できそうな予感がしてきました!
…
……
ちなみにCUDAプログラミングガイドは2022年9月時点で454ページあります…… 😇
SIMD下座術を覚えよう
みなさん、土下座してますか?私は物理的には今のところありませんが、Xデーは明日かもしれません。ここでは数百ページにおよぶマニュアルを読むのがつらすぎる人類に捧ぐ、SIMD下座術を記します!
SIMD下座とは
プログラムの記述から実際にCPU/GPU上で実行するまでの間、コンパイルという作業が存在します。このコンパイルをなさるコンパイラ様は、私のような盆弱なる人間の書いた拙いコードをCPUやGPU上で実行できるよう、機械語あるいは中間言語に翻訳なさる御方です。この翻訳の過程において、コンパイラ様はSIMDが有効活用できそうな部分は自動的に置き換えていただけます(自動ベクトル化)。本章ではコンパイラ様がより良い翻訳を完遂されますよう、拙いコードは拙いコードなりに最低限の作法を踏み、コンパイラ様に失礼のない状態に整える必要があるため、その作法の総称をSIMD下座としています。

1. 場を清める (静的かつ最小限のメモリ確保)
計算に必要な変数を必要な型(ビット数)、必要な最小限の数、静的な大きさで記載します。最終的に動的な大きさを出力する問題であったとしても、
- 部分問題の解決時は静的な大きさの問題に落とし込むようアルゴリズムを考える
- 区切りの良い大きめのサイズで計算し、不要な部分を削除
- あるいはまとまった部分だけは固定長で計算し、端数だけは別途処理
といったことを考えれば、SIMDを活かした計算が可能です。例えばある8ビットの2次元配列の総和を求めるとき、最もシンプルな記述は、数多の情報工学科学生を毒牙にかけたC++を例に、OpenMPによる自動ベクトル化を効かせつつEigenの配列での計算で記述すると以下のようになります。
// 実行時間 0.295ms
uint64_t sum_8bit(const Eigen::Matrix<uint8_t, Eigen::Dynamic, Eigen::Dynamic>& input) {
uint64_t ans = 0;
for (int x = 0; x < input.cols(); x++) {
#pragma omp simd
for (int y = 0; y < input.rows(); y++) {
ans += input(y, x);
}
}
return ans;
}
これは64ビットで定義したans変数に引数のinputの要素を順に加算していき、最終的にすべてのピクセルを走査後にansには総和の値が入る仕組みのプログラムです。コンパイラ様は上記のコードでもそれなりにSIMDを考えた翻訳をされますが、まだSIMD下座力が足りていません。もっと頭を深く下げて次のように記述することが可能です。
// 実行時間 0.156ms
uint64_t sum_8bit(const Eigen::Matrix<uint8_t, Eigen::Dynamic, Eigen::Dynamic>& input) {
uint64_t ans = 0;
for (int x = 0; x < input.cols(); x++) {
// ansに必要な64ビット幅でいきなり計算せず
uint32_t tmp = 0;
#pragma omp simd
for (int y = 0; y < input.rows(); y++) {
// 一時的に狭いビット幅で計算したほうが並列数の多いSIMDになる
tmp += input(y, x);
}
ans += tmp;
}
return ans;
}
上記の記述では行列の列方向の和をtmpという一時的な変数に計算し、その合計値を最終出力のansに都度加算しています。一見何の意味もないように思いますが、tmpの大きさは32ビットで宣言し、ansの半分です。コンピュータ上での計算はデータ型が一致している必要があるので、このように一時的な計算の型をスリムにすることで、SIMD命令実行時の並列計算数を増やすことができます。
2. データをきれいにお供えする (キャッシュを活かす)
独自の構造体の計算でSIMDを効かせたい場合、データ構造アライメントにも注意すべきです。というのも、SIMDでなるべくCPUの計算速度を稼ぐためには、同等程度のスピードでデータも持ってくる必要があり、データはキャッシュが効いていないとほぼ使い物になりません。
キャッシュが効いているとは現金買取で安く買い叩けるということではありません。CPUはなんとなくメモリからデータを直接読み出して計算しているような認識の方も多いと思いますが、我々が部品として意識しているメモリはCPUからすればあくびが出るほど離れた時間距離の場所にあります。よってメモリというのはベットタウンのようなところで、CPUと密な関係にあるのはキャッシュメモリと呼ばれる部分です。つまりキャッシュが効いているとは、このキャッシュメモリに計算Readyなデータが集まっていることを意味します。
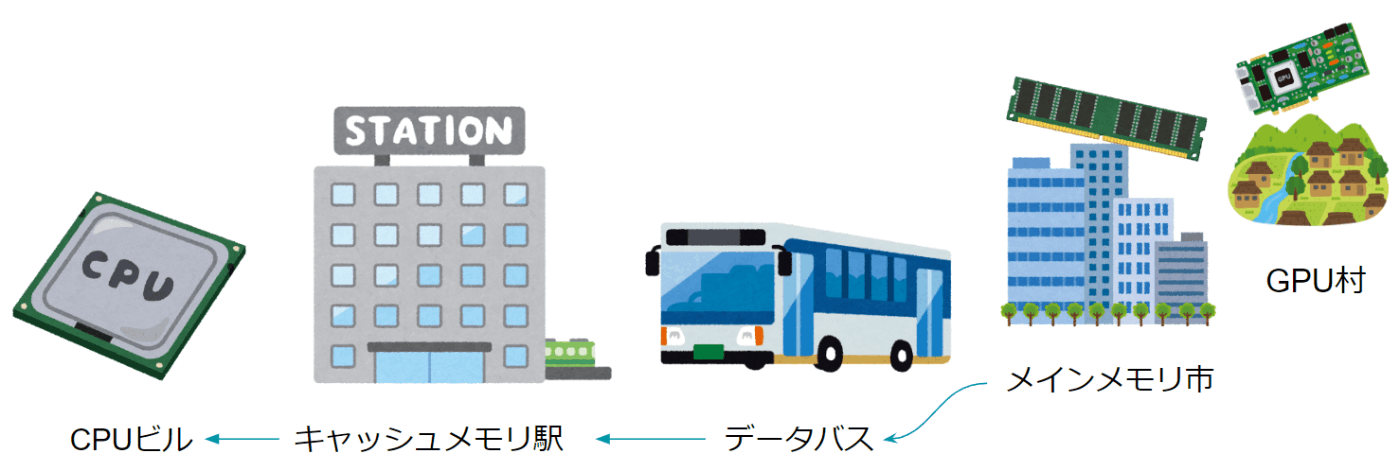
ではこのキャッシュメモリを1TBにすれば良いのでは?というのはそうなのですが、実際のキャッシュメモリはCPUに内蔵されており、令和の時代においてもかなり制限されています(16kBや32kBみたいな単位です)。よって、このキャッシュメモリに何を置くのか?という課題は3度の飯より重要な問題で、基本的には直近読み込まれた部分とその周辺がキャッシュメモリに滞在します。
周辺…… とな?
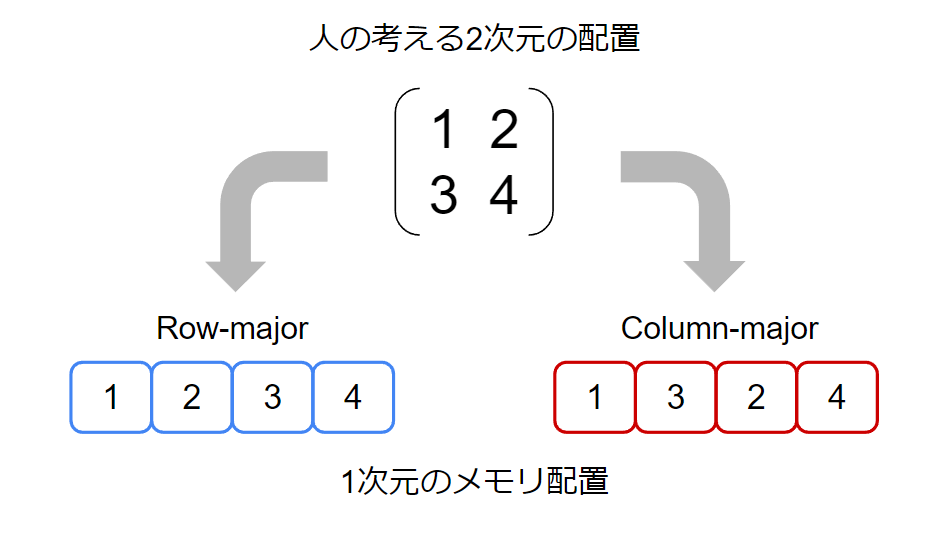
ここでヤード・ポンド法に近しい事例として、Row-majorとColumn-majorという2次元配列をどのようにコンピュータが記憶するかという違いがあり、これによってその周辺が変わります。前節の総和の計算を例に試すと、行あるいは列を走査するかで実行速度が大きく変わります。次にEigenの配列とOpenCVのMatの配列をアクセスした例を示します。
// Eigenでのアクセス例 //////////////////////////////////
// Column-major用のメモリアクセス: 0.327ms
for (int x = 0; x < input.cols(); x++) {
#pragma omp simd
for (int y = 0; y < input.rows(); y++) {
ans += input(y, x);
}
}
// Row-major用のメモリアクセス: 8.483ms
for (int y = 0; y < input.rows(); y++) {
#pragma omp simd
for (int x = 0; x < input.cols(); x++) {
ans += input(y, x);
}
}
// Matでのアクセス例 //////////////////////////////////
// Column-major用のメモリアクセス: 8.177ms
uint64_t sum_8bit_mat(const cv::Mat& input) {
uint64_t ans = 0;
for (int x = 0; x < input.cols; x++) {
#pragma omp simd
for (int y = 0; y < input.rows; y++) {
ans += input.at<unsigned char>(y, x);
}
}
return ans;
}
// Row-major用のメモリアクセス: 0.279ms
uint64_t sum_8bit_mat(const cv::Mat& input) {
uint64_t ans = 0;
for (int y = 0; y < input.rows; y++) {
#pragma omp simd
for (int x = 0; x < input.cols; x++) {
ans += input.at<unsigned char>(y, x);
}
}
return ans;
}
実行時間からわかる通り、Eigenの配列はColumn-majorで記憶されているので、列を走査したほうが圧倒的に高速です。あとちなみにOpenCVのMatはRow-majorです。
私は今のところ無宗教ですが、この世の測量単位と配列のメモリ配置の統一を目指す宗教があれば入信する準備があります。
3. 計算を願い奉る (不可分[atomic]操作を減らす)
不可分操作の多くは「前の状態が決まらなければ次の状態が計算できない」ような問題が対象となります。真に問題がそうであれば仕方がない部分も多いのですが、人間の計算の工夫を汲み取ってもらえないということも考えられます。HLACのマスクパターンが良い例ですが、下記のような4種類のマスクパターンを計算する場合、すべてを個別に計算する方法と、左から右へと差分だけを更新して計算する方法が考えられます。
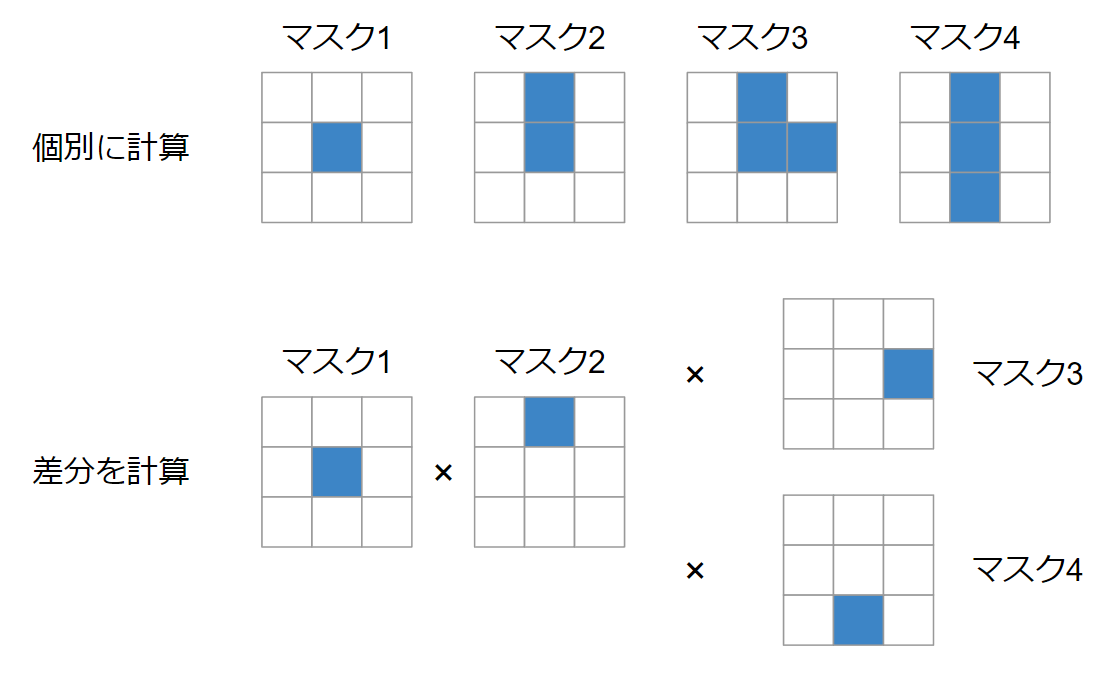
コードに落とし込むと以下のような雰囲気です。
// 個別に計算 (コンパイラ様は不可分操作を意識しない)
Eigen::Matrix<uint64_t, 4, 1> hlac_part(const Eigen::Matrix<uint8_t, Eigen::Dynamic, Eigen::Dynamic>& input) {
Eigen::Matrix<uint64_t, 4, 1> f = Eigen::Matrix<uint64_t, 4, 1>::Zero(4);
const int number_cols = input.cols();
const int number_rows = input.rows();
uint64_t ans = 0;
for (int x = 0; x < (number_cols - 2); x++) {
#pragma omp simd
for (int y = 0; y < (number_rows - 2); y++) {
f[0] += input(y + 1, x + 1);
f[1] += input(y + 0, x + 1) * input(y + 1, x + 1);
f[2] += input(y + 0, x + 1) * input(y + 1, x + 1) * input(y + 1, x + 2);
f[3] += input(y + 0, x + 1) * input(y + 1, x + 1) * input(y + 2, x + 1);
}
}
return f;
}
// 差分を計算 (コンパイラ様からは不可分操作に見えやすい)
Eigen::Matrix<uint64_t, 4, 1> hlac_part(const Eigen::Matrix<uint8_t, Eigen::Dynamic, Eigen::Dynamic>& input) {
Eigen::Matrix<uint64_t, 4, 1> f = Eigen::Matrix<uint64_t, 4, 1>::Zero(4);
const int number_cols = input.cols();
const int number_rows = input.rows();
uint64_t ans = 0;
Eigen::Matrix<uint64_t, 4, 1> tmp = Eigen::Matrix<uint64_t, 4, 1>::Zero(4);
for (int x = 0; x < (number_cols - 2); x++) {
#pragma omp simd
for (int y = 0; y < (number_rows - 2); y++) {
tmp[0] = input(y + 1, x + 1);
tmp[1] = tmp[0] * input(y + 0, x + 1);
tmp[2] = tmp[1] * input(y + 1, x + 2);
tmp[3] = tmp[1] * input(y + 2, x + 1);
f += tmp;
}
}
return f;
}
C++で使用していたIntel Compilerは賢かったのでどちらのコードも同じ速度でしたが、後述するPythonで使用したJITコンパイラでは前者の個別に計算パターンしかうまく高速化できませんでした。というのも、差分計算パターンは計算開始点から順番にマスクを計算しなければ解を計算できないように見える一方、個別計算パターンはそれぞれの計算に依存関係がないように見えるので、SIMDの空きに詰め込める可能性があるからです。
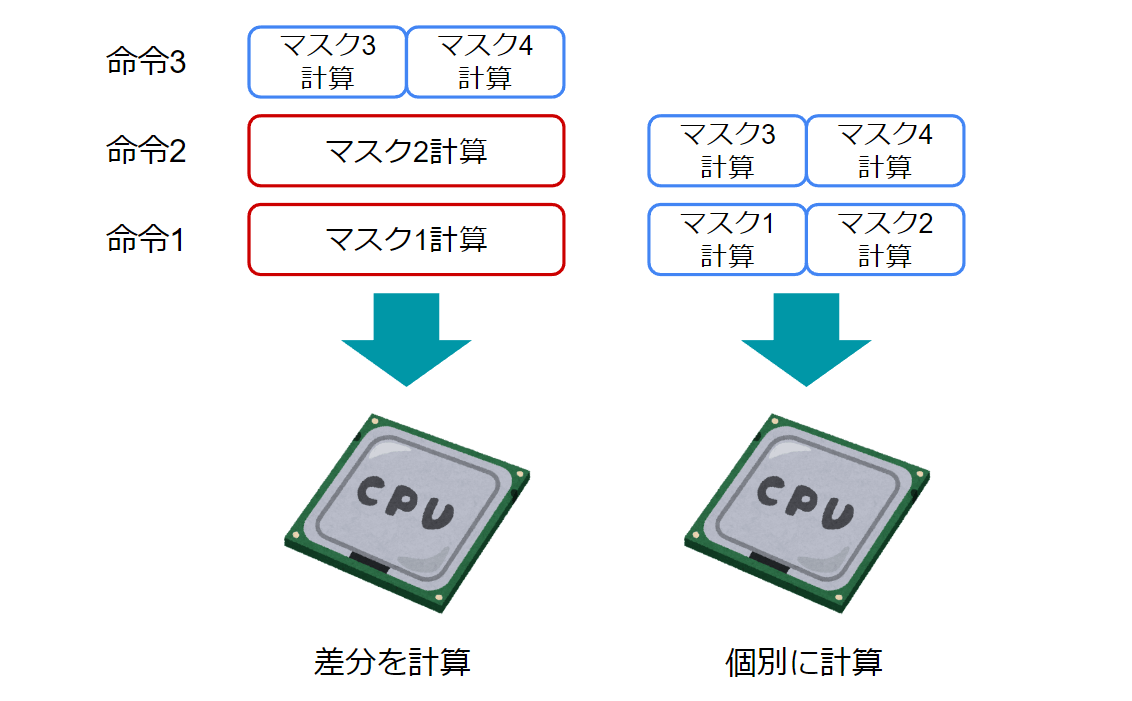
また絶対的な不可分操作であっても、一定のメモリ使用を許せばその成約から逃れられるパターンも多いです。類似例として単純な総和程度でこんな書き方はそもそも不要ですが、何らかの大きな中間結果を保持する必要のある計算では並列処理をする場合も多く、中間結果の計算中に統合までしてしまうと実行効率のロスになります。メモリの使用量が増えるデメリットがありますが、速度を優先するのであれば計算と統合部分は分けて記述すべきです。
// 列方向の総和を計算してからその総和を計算して全体の和を求める場合 ////////
// 不可分操作が含まれる例 実行時間 0.206 ms
uint32_t sum_8bit(const Eigen::Matrix<uint8_t, Eigen::Dynamic, Eigen::Dynamic>& input) {
uint64_t ans = 0;
uint32_t* tmp = new uint32_t[input.cols()]();
int x, y;
#pragma omp parallel for private(y) reduction(+:ans)
for (x = 0; x < input.cols(); x++) {
for (y = 0; y < input.rows(); y++) {
tmp[x] += input(y, x);
}
ans += tmp[x]; // 並列処理はここで一度待機する
}
delete[] tmp;
return ans;
}
// 不可分操作が含まれない例 実行時間 0.160 ms
uint32_t sum_8bit(const Eigen::Matrix<uint8_t, Eigen::Dynamic, Eigen::Dynamic>& input) {
uint64_t ans = 0;
uint32_t* tmp = new uint32_t[input.cols()]();
int x, y;
#pragma omp parallel for private(y)
for (x = 0; x < input.cols(); x++) {
for (y = 0; y < input.rows(); y++) {
tmp[x] += input(y, x);
}
}
for (x = 0; x < input.cols(); x++) {
ans += tmp[x];
}
delete[] tmp;
return ans;
}
濃淡HLACで実践!
今回はPythonとC++でCPUバージョンを実装し、計算機穀潰しと名高いPythonがどの程度SIMD化で改善するのか検証します。合わせてPythonではCUDAを活用したGPUバージョンも実装し、その速度を比較します。コードや実験を確認したい方はPythonもC++も下記のColabにまとめたので確認しながら読み進めてください!
濃淡HLACについては再掲となりますが下記記事の雰囲気です。
HLAC特徴計算はサンプルとして下記の画像を対象とします。

Python -スカラ計算-
まずは最も何もしない方法で計算してみましょう!HLACのパターンをすべて定義すると下記のような3次元配列になります。
import cv2
import numpy as np
# GrayHLACフィルタ定義
hlac_filters = np.array(
[
# 0th order
[[0, 0, 0], [0, 1, 0], [0, 0, 0]],
# 1st order
[[0, 0, 0], [0, 2, 0], [0, 0, 0]],
[[0, 0, 0], [0, 1, 1], [0, 0, 0]],
[[0, 0, 1], [0, 1, 0], [0, 0, 0]],
[[0, 1, 0], [0, 1, 0], [0, 0, 0]],
[[1, 0, 0], [0, 1, 0], [0, 0, 0]],
# 2nd order
[[0, 0, 0], [0, 3, 0], [0, 0, 0]],
[[0, 0, 0], [0, 2, 1], [0, 0, 0]],
[[0, 0, 0], [0, 1, 2], [0, 0, 0]],
[[0, 0, 1], [0, 2, 0], [0, 0, 0]],
[[0, 0, 2], [0, 1, 0], [0, 0, 0]],
[[0, 1, 0], [0, 2, 0], [0, 0, 0]],
[[0, 2, 0], [0, 1, 0], [0, 0, 0]],
[[1, 0, 0], [0, 2, 0], [0, 0, 0]],
[[2, 0, 0], [0, 1, 0], [0, 0, 0]],
[[0, 0, 0], [1, 1, 1], [0, 0, 0]],
[[0, 0, 1], [0, 1, 0], [1, 0, 0]],
[[0, 1, 0], [0, 1, 0], [0, 1, 0]],
[[1, 0, 0], [0, 1, 0], [0, 0, 1]],
[[0, 0, 1], [1, 1, 0], [0, 0, 0]],
[[0, 1, 0], [0, 1, 0], [1, 0, 0]],
[[1, 0, 0], [0, 1, 0], [0, 1, 0]],
[[0, 0, 0], [1, 1, 0], [0, 0, 1]],
[[0, 0, 0], [0, 1, 1], [1, 0, 0]],
[[0, 0, 1], [0, 1, 0], [0, 1, 0]],
[[0, 1, 0], [0, 1, 0], [0, 0, 1]],
[[1, 0, 0], [0, 1, 1], [0, 0, 0]],
[[0, 1, 0], [1, 1, 0], [0, 0, 0]],
[[1, 0, 0], [0, 1, 0], [1, 0, 0]],
[[0, 0, 0], [1, 1, 0], [0, 1, 0]],
[[0, 0, 0], [0, 1, 0], [1, 0, 1]],
[[0, 0, 0], [0, 1, 1], [0, 1, 0]],
[[0, 0, 1], [0, 1, 0], [0, 0, 1]],
[[0, 1, 0], [0, 1, 1], [0, 0, 0]],
[[1, 0, 1], [0, 1, 0], [0, 0, 0]],
],
dtype=np.uint64,
)
これらのマスクパターンの積和を各座標で計算していきます。ポイントとしては
- 画像の走査は3x3のマスク領域がはみ出ないように縦横それぞれ-2の大きさまでアクセス
- 積和は0をかけると0になってしまうので、マスクパターンの1以上の部分のみ計算対象
の2点に注意してください。ピュアなPythonで書くと下記のような記述になります。
def gray_hlac_pure(image, hlac_filters):
r,c = image.shape[:2]
feature = []
for f in hlac_filters:
psum = 0
for y in range(r-2): # 3x3領域ではみ出ないように縦横それぞれ-2の範囲をアクセス
for x in range(c-2):
tmp = 1
for j in range(3): # 3x3のマスクの特徴量計算
for k in range(3):
if f[j,k] > 0: # マスクの値が1以上であれば計算
tmp *= image[y+j, x+k] ** f[j,k]
psum += tmp
feature.append(int(psum))
return feature
……絶望的な速度で動きそうですね
実際に実行し、実行速度を測ってみると、512ピクセル四方の計算に246秒もかかっています。さすが計算機穀潰しの称号は伊達ではありません。
実行結果
[ 3623698 754289870 746573689 743559568 749094091
742141481 167079271408 165292485145 165321237857 164500012860
164497693980 165754379621 165738472799 164225846471 164144575187
162943353739 161204438889 163978125967 160509222466 162306811946
162935623995 162539631265 161933308594 162285103880 162949351203
162470918038 161976833432 164239346530 162572675193 164080968178
161949921686 164221107461 162549812173 164066746393 161979299759]
Elapsed: 246691.523 ms/loop
Python -JITコンパイラでスカラ計算-
世の中は便利なもので、こんなポンコツ速度のプログラムをなんとかしてくれるJITコンパイラというものが存在します。Pythonはインタプリタ言語であるため、プログラムは動くたびに都度次のステップで何をすべきか解釈しながら実行しており、ループ処理の速度を大きく低下させるため、先の結果のようになってしまいます。しかしプログラムの実行時に部分的なコンパイルが可能なJIT(Just-in-time)コンパイラを用いると、先程の速度が嘘のように早くなります。実行にはNumbaが必要になりますが、関数の頭に@njitを付与するだけです。
from jit import njit
@njit
def gray_hlac_jit(image, hlac_filters):
r,c = image.shape[:2]
feature = np.zeros(35, dtype=np.uint64)
count = 0
for f in hlac_filters:
psum = 0
for y in range(r-2):
for x in range(c-2):
tmp = 1
for j in range(3):
for k in range(3):
if f[j,k] > 0:
tmp *= image[y+j, x+k] ** f[j,k]
psum += tmp
feature[count] = psum
count += 1
return feature
実行結果
[ 3623698 754289870 746573689 743559568 749094091
742141481 167079271408 165292485145 165321237857 164500012860
164497693980 165754379621 165738472799 164225846471 164144575187
162943353739 161204438889 163978125967 160509222466 162306811946
162935623995 162539631265 161933308594 162285103880 162949351203
162470918038 161976833432 164239346530 162572675193 164080968178
161949921686 164221107461 162549812173 164066746393 161979299759]
Elapsed: 163.168 ms/loop
163ミリ秒になったので、先程の結果と比べると約1500倍高速です!
これで満足してもいいですが、まだまだ工夫の余地があります。NumbaでもSIMD下座テクニックは有効で、
- 実行時の型を明示し、最小構成にする
- njitではあまり複雑な内容はSIMD化できないので差分計算に置き換える
などすれば実行時間は更に改善されます。
1つ目の部分ではHLACは積和かつ最大3つの掛け算なので、
上記を踏襲すると下記のように27ミリ秒程度になりました!
そろそろ実験段階ではあまり問題にはなりませんが、512ピクセル四方で27ミリではCPUも泣いてしまいます。
@njit('u8[:](u1[:,:])')
def gray_hlac_jit2(img):
feature = np.zeros(35, dtype=np.uint64)
for y in range(img.shape[0]-2):
for x in range(img.shape[1]-2):
tmp = np.zeros(35, dtype=np.uint32) # 8ビット配列であれば32ビットで十分です
# 0th order
tmp[0] = img[y+1,x+1]
# 1st order
tmp[1] = tmp[0] * tmp[0]
tmp[2] = tmp[0] * img[y+1, x+2] # -..
tmp[3] = tmp[0] * img[y, x+2] # -./
tmp[4] = tmp[0] * img[y, x+1] # -.|
tmp[5] = tmp[0] * img[y, x] # \.-
# 2nd order
tmp[6] = tmp[1] * tmp[0]
tmp[7] = tmp[2] * tmp[0]
tmp[8] = tmp[2] * img[y+1, x+2]
tmp[9] = tmp[3] * tmp[0]
tmp[10] = tmp[3] * img[y, x+2]
tmp[11] = tmp[4] * tmp[0]
tmp[12] = tmp[4] * img[y, x+1]
tmp[13] = tmp[5] * tmp[0]
tmp[14] = tmp[5] * img[y, x]
tmp[15] = tmp[2] * img[y+1, x]
tmp[16] = tmp[3] * img[y+2, x]
tmp[17] = tmp[4] * img[y+2, x+1]
tmp[18] = tmp[5] * img[y+2, x+2]
tmp[19] = tmp[3] * img[y+1, x]
tmp[20] = tmp[4] * img[y+2, x]
tmp[21] = tmp[5] * img[y+2, x+1]
c_rd = tmp[0] * img[y+2, x+2] # -.\
tmp[22] = c_rd * img[y+1, x]
tmp[23] = tmp[2] * img[y+2, x]
tmp[24] = tmp[3] * img[y+2, x+1]
tmp[25] = tmp[4] * img[y+2, x+2]
tmp[26] = tmp[2] * img[y, x]
tmp[27] = tmp[4] * img[y+1, x]
tmp[28] = tmp[5] * img[y+2, x]
tmp[29] = tmp[0] * img[y+1, x] * img[y+2, x+1]
tmp[30] = c_rd * img[y+2, x]
tmp[31] = tmp[2] * img[y+2, x+1]
tmp[32] = tmp[3] * img[y+2, x+2]
tmp[33] = tmp[4] * img[y+1, x+2]
tmp[34] = tmp[3] * img[y, x]
feature += tmp
return feature
実行結果
[ 3623698 754289870 746573689 743559568 749094091
742141481 167079271408 165292485145 165321237857 164500012860
164497693980 165754379621 165738472799 164225846471 164144575187
162943353739 161204438889 163978125967 160509222466 162306811946
162935623995 162539631265 161933308594 162285103880 162949351203
162470918038 161976833432 164239346530 162572675193 164080968178
161949921686 164221107461 162549812173 164066746393 161979299759]
Elapsed: 27.128 ms/loop
Python -JITコンパイラでベクトル計算-
ついにこれまでの礼儀作法を遵守するときがやってきました!JITコンパイラ様はあまり難しいことを考える御方ではないので、ある程度プログラマがお気持ちをコードを通じて伝える必要がある点が難しいですが、
- それぞれのマスクパターンは並列に計算しても良い
ことを伝えるために
- 個別計算パターンをコードで教える
- 一時変数も分割して独立に計算可能なことを明示する
といった要点を踏まえ、Numbaのguvectorizeで作成することで無事SIMD化されました。実行時間はなんと4ms台と実用十分な速度まで改善しました!
…
…… ちょっと目を細めてみればC言語のような気がしますが気のせいでしょう
from jit import guvectorize
@guvectorize(['void(u1[:,:], u8[:], u8[:])'], '(x,y),(z)->(z)', nopython=True)
def gray_hlac_vectorized(img, a, feature):
tmp0, tmp1, tmp2, tmp3, tmp4, tmp5, tmp6, tmp7, tmp8, tmp9 = 0,0,0,0,0,0,0,0,0,0
tmp10, tmp11, tmp12, tmp13, tmp14, tmp15, tmp16, tmp17, tmp18, tmp19 = 0,0,0,0,0,0,0,0,0,0
tmp20, tmp21, tmp22, tmp23, tmp24, tmp25, tmp26, tmp27, tmp28, tmp29 = 0,0,0,0,0,0,0,0,0,0
tmp30, tmp31, tmp32, tmp33, tmp34 = 0,0,0,0,0
for y in range(img.shape[0]-2):
for x in range(img.shape[1]-2):
# 0th order
tmp0 += img[y+1,x+1]
# 1st order
tmp1 += img[y+1,x+1] * img[y+1,x+1]
tmp2 += img[y+1,x+1] * img[y+1, x+2] # -..
tmp3 += img[y+1,x+1] * img[y, x+2] # -./
tmp4 += img[y+1,x+1] * img[y, x+1] # -.|
tmp5 += img[y+1,x+1] * img[y, x] # \.-
# 2nd order
tmp6 += img[y+1,x+1] * img[y+1,x+1] * img[y+1,x+1]
tmp7 += img[y+1,x+1] * img[y+1, x+2] * img[y+1,x+1]
tmp8 += img[y+1,x+1] * img[y+1, x+2] * img[y+1, x+2]
tmp9 += img[y+1,x+1] * img[y, x+2] * img[y+1,x+1]
tmp10 += img[y+1,x+1] * img[y, x+2] * img[y, x+2]
tmp11 += img[y+1,x+1] * img[y, x+1] * img[y+1,x+1]
tmp12 += img[y+1,x+1] * img[y, x+1] * img[y, x+1]
tmp13 += img[y+1,x+1] * img[y, x] * img[y+1,x+1]
tmp14 += img[y+1,x+1] * img[y, x] * img[y, x]
tmp15 += img[y+1,x+1] * img[y+1, x+2] * img[y+1, x]
tmp16 += img[y+1,x+1] * img[y, x+2] * img[y+2, x]
tmp17 += img[y+1,x+1] * img[y, x+1] * img[y+2, x+1]
tmp18 += img[y+1,x+1] * img[y, x] * img[y+2, x+2]
tmp19 += img[y+1,x+1] * img[y, x+2] * img[y+1, x]
tmp20 += img[y+1,x+1] * img[y, x+1] * img[y+2, x]
tmp21 += img[y+1,x+1] * img[y, x] * img[y+2, x+1]
tmp22 += img[y+1,x+1] * img[y+2, x+2] * img[y+1, x]
tmp23 += img[y+1,x+1] * img[y+1, x+2] * img[y+2, x]
tmp24 += img[y+1,x+1] * img[y, x+2] * img[y+2, x+1]
tmp25 += img[y+1,x+1] * img[y, x+1] * img[y+2, x+2]
tmp26 += img[y+1,x+1] * img[y+1, x+2] * img[y, x]
tmp27 += img[y+1,x+1] * img[y, x+1] * img[y+1, x]
tmp28 += img[y+1,x+1] * img[y, x] * img[y+2, x]
tmp29 += img[y+1,x+1] * img[y+1, x] * img[y+2, x+1]
tmp30 += img[y+1,x+1] * img[y+2, x+2] * img[y+2, x]
tmp31 += img[y+1,x+1] * img[y+1, x+2] * img[y+2, x+1]
tmp32 += img[y+1,x+1] * img[y, x+2] * img[y+2, x+2]
tmp33 += img[y+1,x+1] * img[y, x+1] * img[y+1, x+2]
tmp34 += img[y+1,x+1] * img[y, x+2] * img[y, x]
feature[0] = tmp0
feature[1] = tmp1
feature[2] = tmp2
feature[3] = tmp3
feature[4] = tmp4
feature[5] = tmp5
feature[6] = tmp6
feature[7] = tmp7
feature[8] = tmp8
feature[9] = tmp9
feature[10] = tmp10
feature[11] = tmp11
feature[12] = tmp12
feature[13] = tmp13
feature[14] = tmp14
feature[15] = tmp15
feature[16] = tmp16
feature[17] = tmp17
feature[18] = tmp18
feature[19] = tmp19
feature[20] = tmp20
feature[21] = tmp21
feature[22] = tmp22
feature[23] = tmp23
feature[24] = tmp24
feature[25] = tmp25
feature[26] = tmp26
feature[27] = tmp27
feature[28] = tmp28
feature[29] = tmp29
feature[30] = tmp30
feature[31] = tmp31
feature[32] = tmp32
feature[33] = tmp33
feature[34] = tmp34
実行結果
[ 3623698 754289870 746573689 743559568 749094091
742141481 167079271408 165292485145 165321237857 164500012860
164497693980 165754379621 165738472799 164225846471 164144575187
162943353739 161204438889 163978125967 160509222466 162306811946
162935623995 162539631265 161933308594 162285103880 162949351203
162470918038 161976833432 164239346530 162572675193 164080968178
161949921686 164221107461 162549812173 164066746393 161979299759]
Elapsed: 4.134 ms/loop
Python -CUDAで計算-
ここからはGPU実装です。残念ながらGPU実装では実装したものがSIMDと等価であるので、あまりSIMD下座テクニックはありません。しかし、GPGPUの利用には通常様々な環境セットアップが面倒なところ、Pythonであれば手間なく可能であり、それらのテクニックについてご紹介します。
今回はCUDAへの実装にCuPyを使用します。NumbaでもCUDA実装は可能なのですが、CuPyのほうが基本的な行列演算が実装済みであるため、必要な部分の実装に集中することができます。
さて、GPU上で動くコードですが、今回は特に高速化等を意識せず書いてみます。CPUと実装が異なる点として、CPUではマスクあたりのHLAC特徴量計算とその総和をほぼ同時に計算していましたが、それらをGPUではマスクごとHLAC特徴量計算と総和の2タスクに分割します。
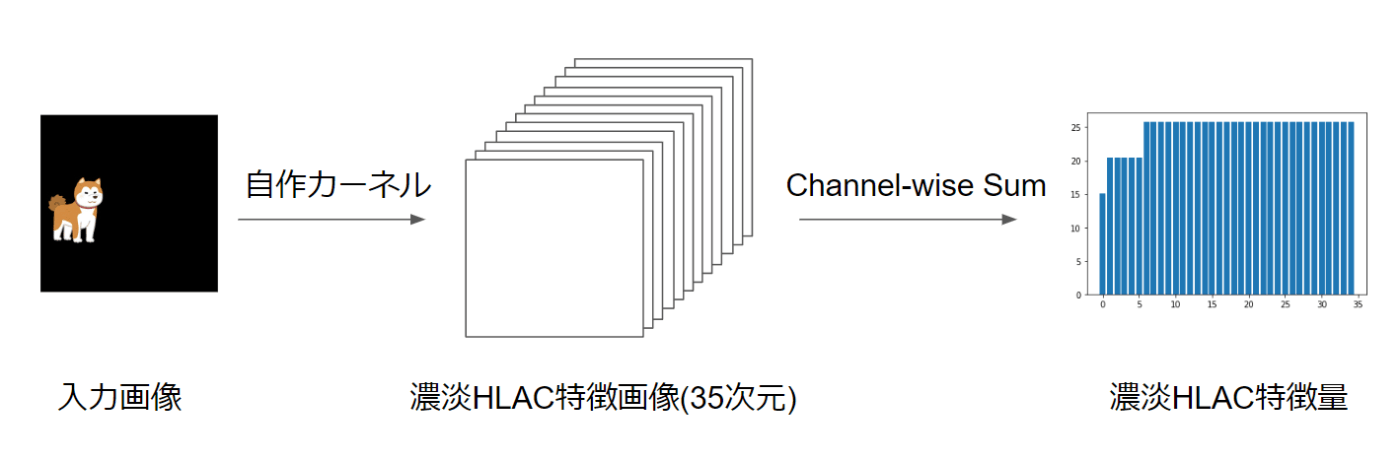
GPU上でプログラムを動かすためにはカーネルと呼ばれるプログラムを書く必要がありますが、実質C言語です。処理が長いだけで典型的な二次元配列用のCUDAカーネルです。各ピクセルごとの計算では上から順に処理していくだけなので、ここは計算量の少ない差分計算作戦が有効です。
extern "C" __global__ void gray_hlac(const unsigned char *input, unsigned long long *output, const unsigned int row, const unsigned int col, const unsigned int d)
{
int x = blockDim.x * blockIdx.x + threadIdx.x;
int y = blockDim.y * blockIdx.y + threadIdx.y;
if (x < col - 2 && y < row - 2)
{
// 0th order
output[y * col + x + (0 * d)] = input[(y + 1) * col + (x + 1)];
// 1st order
output[y * col + x + (1 * d)] = output[y * col + x + (0 * d)] * input[(y + 1) * col + (x + 1)];
output[y * col + x + (2 * d)] = output[y * col + x + (0 * d)] * input[(y + 1) * col + (x + 2)];
output[y * col + x + (3 * d)] = output[y * col + x + (0 * d)] * input[(y + 0) * col + (x + 2)];
output[y * col + x + (4 * d)] = output[y * col + x + (0 * d)] * input[(y + 0) * col + (x + 1)];
output[y * col + x + (5 * d)] = output[y * col + x + (0 * d)] * input[(y + 0) * col + (x + 0)];
// 2nd order
output[y * col + x + (6 * d)] = output[y * col + x + (1 * d)] * input[(y + 1) * col + (x + 1)];
output[y * col + x + (7 * d)] = output[y * col + x + (2 * d)] * output[y * col + x + (0 * d)];
output[y * col + x + (8 * d)] = output[y * col + x + (2 * d)] * input[(y + 1) * col + (x + 2)];
output[y * col + x + (9 * d)] = output[y * col + x + (3 * d)] * output[y * col + x + (0 * d)];
output[y * col + x + (10 * d)] = output[y * col + x + (3 * d)] * input[(y + 0) * col + (x + 2)];
output[y * col + x + (11 * d)] = output[y * col + x + (4 * d)] * output[y * col + x + (0 * d)];
output[y * col + x + (12 * d)] = output[y * col + x + (4 * d)] * input[(y + 0) * col + (x + 1)];
output[y * col + x + (13 * d)] = output[y * col + x + (5 * d)] * output[y * col + x + (0 * d)];
output[y * col + x + (14 * d)] = output[y * col + x + (5 * d)] * input[(y + 0) * col + (x + 0)];
output[y * col + x + (15 * d)] = output[y * col + x + (2 * d)] * input[(y + 1) * col + (x + 0)];
output[y * col + x + (16 * d)] = output[y * col + x + (3 * d)] * input[(y + 2) * col + (x + 0)];
output[y * col + x + (17 * d)] = output[y * col + x + (4 * d)] * input[(y + 2) * col + (x + 1)];
output[y * col + x + (18 * d)] = output[y * col + x + (5 * d)] * input[(y + 2) * col + (x + 2)];
output[y * col + x + (19 * d)] = output[y * col + x + (3 * d)] * input[(y + 1) * col + (x + 0)];
output[y * col + x + (20 * d)] = output[y * col + x + (4 * d)] * input[(y + 2) * col + (x + 0)];
output[y * col + x + (21 * d)] = output[y * col + x + (5 * d)] * input[(y + 2) * col + (x + 1)];
unsigned long long c_rd = output[y * col + x + (0 * d)] * input[(y + 2) * col + (x + 2)];
output[y * col + x + (22 * d)] = c_rd * input[(y + 1) * col + (x + 0)];
output[y * col + x + (23 * d)] = output[y * col + x + (2 * d)] * input[(y + 2) * col + (x + 0)];
output[y * col + x + (24 * d)] = output[y * col + x + (3 * d)] * input[(y + 2) * col + (x + 1)];
output[y * col + x + (25 * d)] = output[y * col + x + (4 * d)] * input[(y + 2) * col + (x + 2)];
output[y * col + x + (26 * d)] = output[y * col + x + (2 * d)] * input[(y + 0) * col + (x + 0)];
output[y * col + x + (27 * d)] = output[y * col + x + (4 * d)] * input[(y + 1) * col + (x + 0)];
output[y * col + x + (28 * d)] = output[y * col + x + (5 * d)] * input[(y + 2) * col + (x + 0)];
output[y * col + x + (29 * d)] = output[y * col + x + (0 * d)] * input[(y + 1) * col + (x + 0)] * input[(y + 2) * col + (x + 1)];
output[y * col + x + (30 * d)] = c_rd * input[(y + 2) * col + (x + 0)];
output[y * col + x + (31 * d)] = output[y * col + x + (2 * d)] * input[(y + 2) * col + (x + 1)];
output[y * col + x + (32 * d)] = output[y * col + x + (3 * d)] * input[(y + 2) * col + (x + 2)];
output[y * col + x + (33 * d)] = output[y * col + x + (4 * d)] * input[(y + 1) * col + (x + 2)];
output[y * col + x + (34 * d)] = output[y * col + x + (3 * d)] * input[(y + 0) * col + (x + 0)];
}
}
上記のカーネル+総和を実行するとついに2ms台が出ました!
(ColabのGPU環境では時間やタイミングでかなり実行時間がばらつきます)
しかし思ったよりは早くないような気もしますが、この原因については後述したいと思います。
実行結果
[ 3623698 754289870 746573689 743559568 749094091
742141481 167079271408 165292485145 165321237857 164500012860
164497693980 165754379621 165738472799 164225846471 164144575187
162943353739 161204438889 163978125967 160509222466 162306811946
162935623995 162539631265 161933308594 162285103880 162949351203
162470918038 161976833432 164239346530 162572675193 164080968178
161949921686 164221107461 162549812173 164066746393 161979299759]
Elapsed: 2.177 ms/loop
C++ローカル環境で実施したい場合
Windows環境にてOpenCVの自前ビルドをしたくなければ、Visual Studio 2019のインストールをおすすめします。その他、OpenMPを用いた自動ベクトル化にはIntel OneAPIのIntel C++ Compilerがほぼ必須です。
C++ -スカラ計算-
全体像はColabを見ていただいて、ここではロジック部分のみ記載します。
C++の単純計算では、3x3の領域を取り出し、部分ごとのHLAC特徴ベクトルを返すような仕組みにしています。実行時間は約9msとPythonのJITコンパイラのスカラ計算の27msよりは3倍程度高速でした。
Eigen::Matrix<uint64_t, 35, 1> eval_gray_hlac(const Eigen::Matrix<uint8_t, 3, 3>& d) {
Eigen::Matrix<uint64_t, 35, 1> f;
// 0th order
f(0) = d(1, 1);
// 1st order
f(1) = f(0) * f(0);
f(2) = f(0) * d(1, 2);
f(3) = f(0) * d(0, 2);
f(4) = f(0) * d(0, 1);
f(5) = f(0) * d(0, 0);
// 2nd order
f(6) = f(1) * f(0);
f(7) = f(0) * f(2);
f(8) = f(2) * d(1, 2);
f(9) = f(0) * f(3);
f(10) = f(3) * d(0, 2);
f(11) = f(0) * f(4);
f(12) = f(4) * d(0, 1);
f(13) = f(0) * f(5);
f(14) = f(5) * d(0, 0);
f(15) = f(2) * d(1, 0);
f(16) = f(3) * d(2, 0);
f(17) = f(4) * d(2, 1);
f(18) = f(5) * d(2, 2);
f(19) = f(3) * d(1, 0);
f(20) = f(4) * d(2, 0);
f(21) = f(5) * d(2, 1);
f(22) = f(0) * d(2, 2) * d(1, 0);
f(23) = f(2) * d(2, 0);
f(24) = f(3) * d(2, 1);
f(25) = f(4) * d(2, 2);
f(26) = f(2) * d(0, 0);
f(27) = f(4) * d(1, 0);
f(28) = f(5) * d(2, 0);
f(29) = f(0) * d(1, 0) * d(2, 1);
f(30) = f(0) * d(2, 2) * d(2, 0);
f(31) = f(2) * d(2, 1);
f(32) = f(3) * d(2, 2);
f(33) = f(4) * d(1, 2);
f(34) = f(3) * d(0, 0);
return f;
}
Eigen::Matrix<uint64_t, 35, 1> gray_hlac(const cv::Mat& input) {
Eigen::Matrix<uint64_t, 35, 1> feature = Eigen::Matrix<uint64_t, 35, 1>::Zero(35);
const int number_cols = input.cols;
const int number_rows = input.rows;
Eigen::Matrix<uint8_t, Eigen::Dynamic, Eigen::Dynamic> d;
cv::cv2eigen(input, d);
int y, x;
Eigen::Matrix<uint64_t, 35, 1> f;
for (y = 0; y < number_rows - 2; y++) {
for (x = 0; x < number_cols - 2; x++) {
feature += eval_gray_hlac(d.block<3, 3>(x, y)); //3x3の領域を切り出して計算
}
}
return feature;
}
実行結果
AVX SSE, SSE2, SSE3, SSSE3, SSE4.1, SSE4.2
3623698
754289870
746573689
743559568
749094091
742141481
167079271408
165292485145
165321237857
164500012860
164497693980
165754379621
165738472799
164225846471
164144575187
162943353739
161204438889
163978125967
160509222466
162306811946
162935623995
162539631265
161933308594
162285103880
162949351203
162470918038
161976833432
164239346530
162572675193
164080968178
161949921686
164221107461
162549812173
164066746393
161979299759
8.68211[ms/loop]
C++ -OpenMPでベクトル計算-
C++でも同様にPythonと同じ要領で個別計算パターンを記載していますが、Intel Compilerを使用する限りでは差分計算パターンでも同程度の実行時間でした。一つポイントとしてはOpenMPのSIMDの修飾にsafelenというものを加えています。
safelenはSIMD化した際の並列データ数の安全な範囲を指示するもので、冒頭の64ビットCPUの説明では1度に64ビットの処理が可能なCPUとざっくり説明を記載していましたが、詳細にはSIMD用の計算空間は拡張命令ごとに異なり、2013年以降のCPUでほぼ実行可能なAVX/AVX2では256ビットの空間があります。このAVXの利用を前提とすると、HLAC特徴ベクトルを今回は64ビットのデータで定義しているため、単純計算で4つまでは並列可能なことになります。不明であれば無理に指示する必要はないのですが、プログラマが明示的に指定したほうがパフォーマンスは向上します。
色々と長くなりましたが、C++のSIMD実装は約2msとかなり高速で、PythonのSIMD実装(4ms)の2倍程度の性能があります。
#pragma omp declare simd
int point2d(const int y, const int x, const int ncols) {
return y * ncols + x;
}
Eigen::Matrix<uint64_t, 35, 1> gray_hlac(const cv::Mat& input) {
Eigen::Matrix<uint64_t, 35, 1> f = Eigen::Matrix<uint64_t, 35, 1>::Zero(35);
const int ncols = input.cols;
const int nrows = input.rows;
int x,y;
for (y = 0; y < (nrows - 2); y++) {
#pragma omp simd safelen(4)
for (x = 0; x < (ncols - 2); x++) {
// 0th order
f[0] += input.data[point2d(y + 1, x + 1, ncols)];
// 1st order
f[1] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y + 1, x + 1, ncols)];
f[2] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y + 1, x + 2, ncols)];
f[3] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x + 2, ncols)];
f[4] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x + 1, ncols)];
f[5] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x, ncols)];
// 2nd order
f[6] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y + 1, x + 1, ncols)];
f[7] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y + 1, x + 2, ncols)];
f[8] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y + 1, x + 2, ncols)] * input.data[point2d(y + 1, x + 2, ncols)];
f[9] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x + 2, ncols)];
f[10] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x + 2, ncols)] * input.data[point2d(y, x + 2, ncols)];
f[11] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x + 1, ncols)];
f[12] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x + 1, ncols)] * input.data[point2d(y, x + 1, ncols)];
f[13] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x, ncols)];
f[14] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x, ncols)] * input.data[point2d(y, x, ncols)];
f[15] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y + 1, x + 2, ncols)] * input.data[point2d(y + 1, x, ncols)];
f[16] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x + 2, ncols)] * input.data[point2d(y + 2, x, ncols)];
f[17] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x + 1, ncols)] * input.data[point2d(y + 2, x + 1, ncols)];
f[18] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x, ncols)] * input.data[point2d(y + 2, x + 2, ncols)];
f[19] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x + 2, ncols)] * input.data[point2d(y + 1, x, ncols)];
f[20] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x + 1, ncols)] * input.data[point2d(y + 2, x, ncols)];
f[21] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x, ncols)] * input.data[point2d(y + 2, x + 1, ncols)];
f[22] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y + 2, x + 2, ncols)] * input.data[point2d(y + 1, x, ncols)];
f[23] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y + 1, x + 2, ncols)] * input.data[point2d(y + 2, x, ncols)];
f[24] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x + 2, ncols)] * input.data[point2d(y + 2, x + 1, ncols)];
f[25] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x + 1, ncols)] * input.data[point2d(y + 2, x + 2, ncols)];
f[26] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y + 1, x + 2, ncols)] * input.data[point2d(y, x, ncols)];
f[27] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x + 1, ncols)] * input.data[point2d(y + 1, x, ncols)];
f[28] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x, ncols)] * input.data[point2d(y + 2, x, ncols)];
f[29] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y + 1, x, ncols)] * input.data[point2d(y + 2, x + 1, ncols)];
f[30] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y + 2, x + 2, ncols)] * input.data[point2d(y + 2, x, ncols)];
f[31] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y + 1, x + 2, ncols)] * input.data[point2d(y + 2, x + 1, ncols)];
f[32] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x + 2, ncols)] * input.data[point2d(y + 2, x + 2, ncols)];
f[33] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x + 1, ncols)] * input.data[point2d(y + 1, x + 2, ncols)];
f[34] += input.data[point2d(y + 1, x + 1, ncols)] * input.data[point2d(y, x + 2, ncols)] * input.data[point2d(y, x, ncols)];
}
}
return f;
}
実行結果
AVX SSE, SSE2, SSE3, SSSE3, SSE4.1, SSE4.2
3623698
754289870
746573689
743559568
749094091
742141481
167079271408
165292485145
165321237857
164500012860
164497693980
165754379621
165738472799
164225846471
164144575187
162943353739
161204438889
163978125967
160509222466
162306811946
162935623995
162539631265
161933308594
162285103880
162949351203
162470918038
161976833432
164239346530
162572675193
164080968178
161949921686
164221107461
162549812173
164066746393
161979299759
1.85671[ms/loop]
性能比較
画像の解像度を変えて最大8Kまで引き伸ばして計算した結果を下記にまとめました。
Google Colabはインスタンス相乗り状態であり、実行時間は降ってくるリソース次第でかなり変わるので参考値程度です。GPUの場合はVRAMの枯渇から8K解像度ではOOM(メモリ不足)が発生しています。これはGPUの問題というよりプログラムの問題で、中間処理で35次元の領域を確保するためです。線形補間すれば4096の結果の4倍程度の見積もりになります。
Google Colabでの実施例: 時間が特にかかるもの以外は100ループの平均時間[ms/loop]
| 解像度 [px] | 512 | 1024 | 2048 | 4096 | 8192 |
|---|---|---|---|---|---|
| Python: Pure | 241742.19 | - | - | - | - |
| Python: JIT | 26.62 | 116.78 | 435.38 | 1739.62 | 7056.52 |
| Python: JIT Vecotrized | 4.32 | 16.56 | 65.96 | 263.03 | 1034.12 |
| Python: GPU | 2.31 | 4.89 | 16.30 | 63.33 | OOM |
| C++: Pure | 8.63 | 26.64 | 108.92 | 452.85 | 1913.82 |
| C++: Vectorized | 2.13 | 8.67 | 31.97 | 132.69 | 408.58 |
なお実行時のCPUはIntel Xeon CPU @ 2.20GHz(Family:6, Model:79)、GPUはNVIDIA Tesla T4でした。テーブルでは見ずらいのでそれぞれ条件ごとに可視化してみましょう。
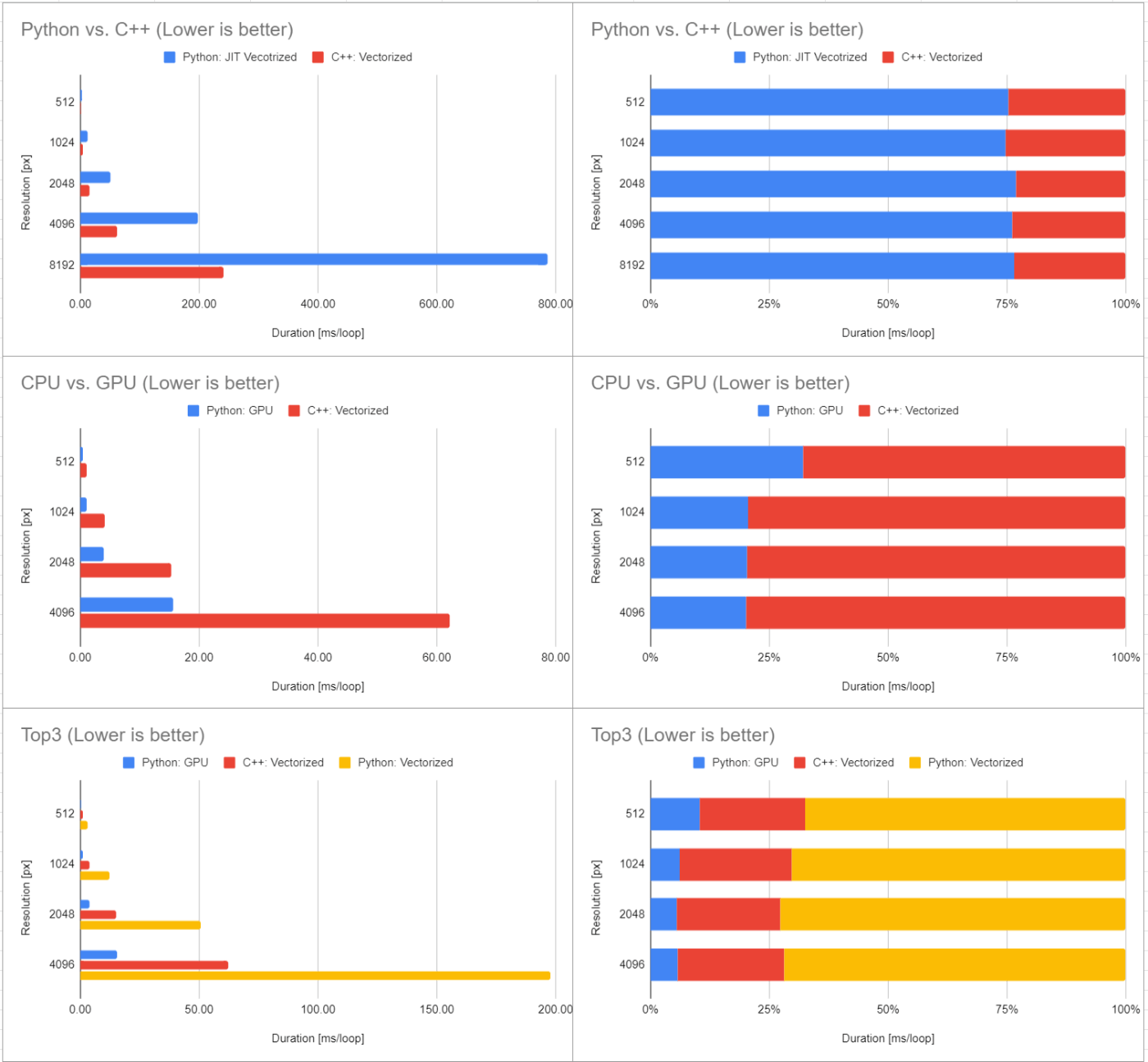
Python vs.C++
まずは個人的に興味のあったPythonとC++での最速プログラムのCPU上での実行時間の比較です。PythonというよりはJITコンパイラ vs Intel C++ Compilerという見方が正しいかもしれませんが、案外Pythonも健闘していることに驚きです。おおよそPythonでは2~3倍程度の時間を要していますが、傾向的にはさらに高解像度な対象で実行時間の差が開いていきそうです。
実行時間
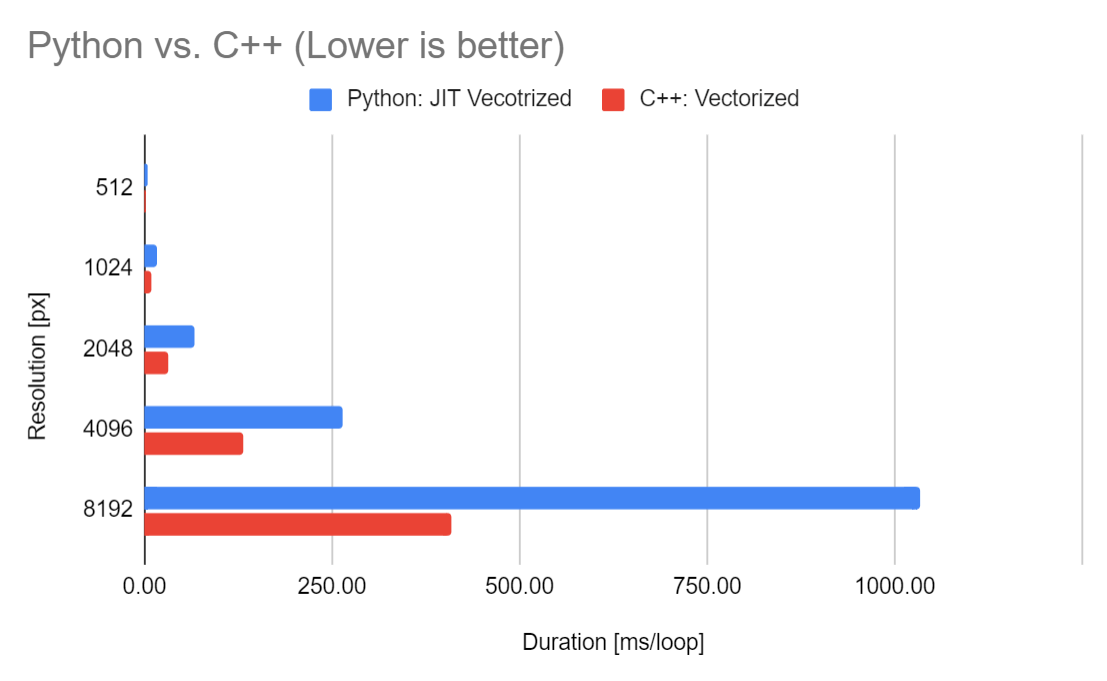
実行時間割合

CPU vs. GPU
C++とPythonのGPU実行での比較です。おおよそGPU実行では2倍の性能向上がありますが、512ピクセルの解像度では立場が逆転し、CPUの実行時間のほうが早い傾向にあります。これはGPUの実行時間には対象を処理する以外に、データを転送するための時間が必要となるためです。
どういうことかはキャッシュの話で出した下記の図を振り返りたいと思います。

CPUでは実行時にはキャッシュに処理対象となるデータを格納する必要がありましたが、ではGPUではどうでしょうか?察しの良い読者の皆様もうお気づきと思いますが、やはりGPUにもキャッシュメモリと同等の部位が存在し、そこにデータを転送する必要があります。そしてGPU村と田舎感を出しているように、CPUから見てGPUはそこそこ遠い位置にあります。よって小さなデータではGPU村へデータを輸送中にCPUビルで処理が完了するということが起こりえます。
以上から今回の環境ではおおよそ512ピクセル四方以下の画像はCPUで処理し、それ以上の画像はGPUで処理したほうが良いということになります。あぁややこしや……
実行時間
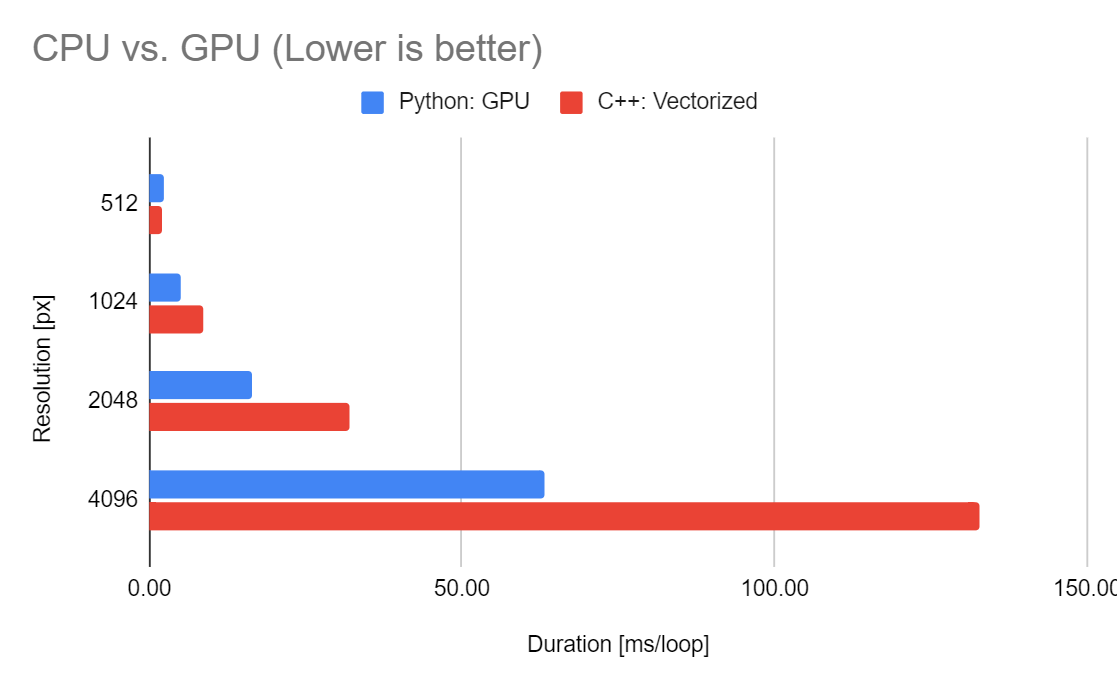
実行時間割合
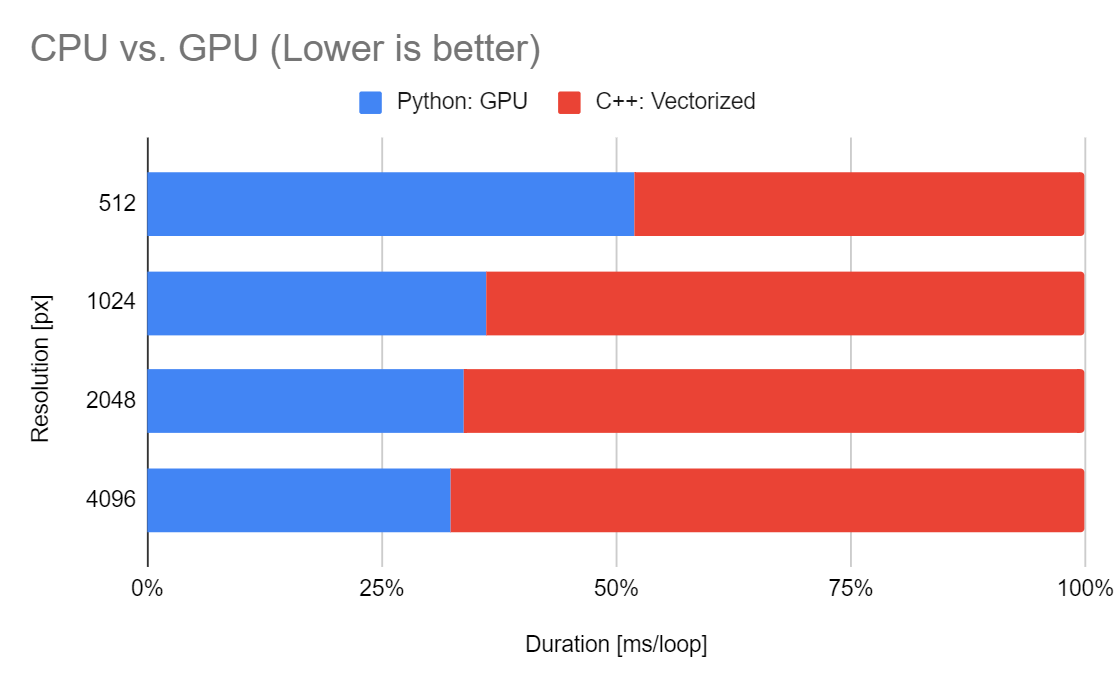
Top3
最後にとりあえず上位3つのプログラムを並べた可視化です。やはりGPUが高解像度側では早いのですが、CPUでもフルHDの映像をおおよそ16msで処理できる見積もりになるので、GPUにコストを払うほどの恩恵をうける場面は少ないかもしれません。4K動画においてもリアルタイムに処理したいような要件であれば検討の価値がありそうです。
実行時間
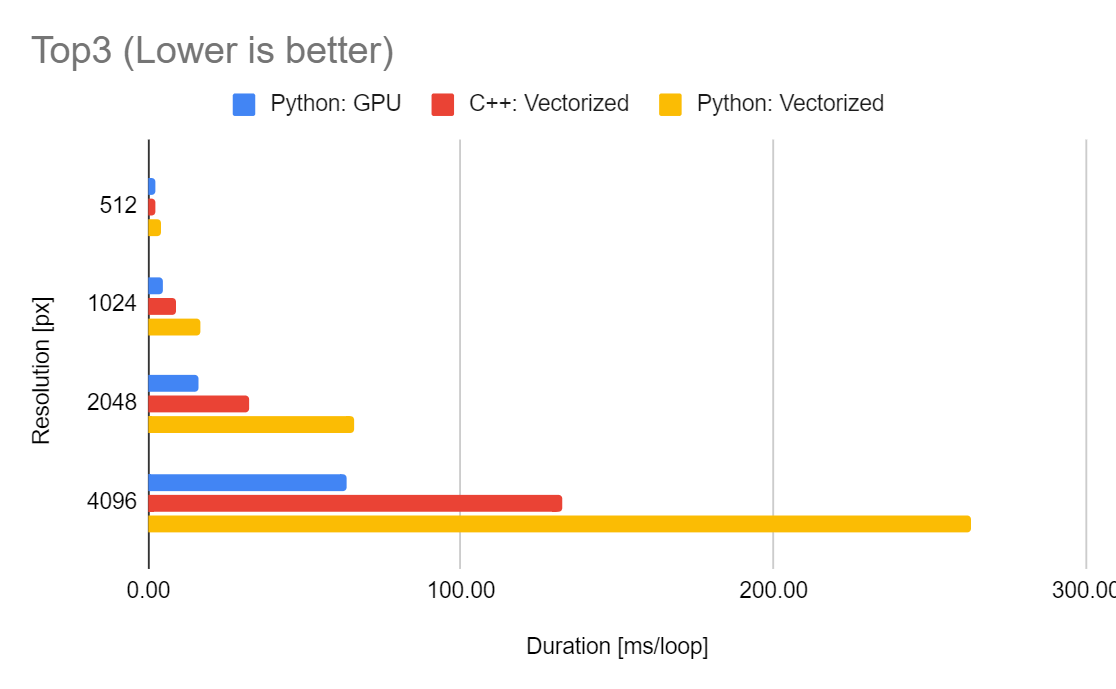
実行時間割合

ローカルPCでの実施例
ローカルPCでもベンチマークしたので掲載しておきます。
CPUはRyzen 3600X、GPUはRTX 3080Tiで、GPUのCUDAコア数がColab環境よりも多い分、処理時間の高速化が顕著に見えています。
ローカルPCでの実施例: 時間が特にかかるもの以外は100ループの平均時間[ms/loop]
| 解像度 [px] | 512 | 1024 | 2048 | 4096 | 8192 |
|---|---|---|---|---|---|
| Python: Pure | 259446.23 | - | - | - | - |
| Python: JIT | 28.47 | 95.70 | 385.14 | 1557.81 | 6168.21 |
| Python: JIT Vecotrized | 3.11 | 12.11 | 50.81 | 197.95 | 785.70 |
| Python: GPU | 0.48 | 1.06 | 3.91 | 15.57 | OOM |
| C++: Pure | 3.36 | 15.10 | 51.82 | 205.08 | 840.06 |
| C++: Vectorized | 1.02 | 4.09 | 15.28 | 62.12 | 241.28 |
まとめ
いかがだったでしょうか!
今回は濃淡HLACの実装を例とした、CPUとGPUでのプログラムを実装して比較しました
- CPUとGPUではそれぞれ直列、並列実行の高速処理が得意
- CPUもSIMDという拡張命令を活用すれば並列処理がかなり早くなる(ベクトル化)
- GPUまでのデータ転送速度を考えるとGPUは高解像度側、CPUは低解像度側で速度有利
であることがざっくりと分かればバッチリです!
実装まで踏み込む場合はなるべくコンパイラ任せで楽して自動ベクトル化をするためのTipsをまとめました。
- 必要最小限のビット幅を見積もり静的なメモリ確保をする
- キャッシュが効きやすいデータ構造で入力&アクセスする
- 不可分操作は極力避ける記述をする
ことで十分実用範囲に足りうる速度のプログラムが作成できます。
本記事がCPU/GPUプログラム作成の足がかりになると幸いです!
メンバー募集中です!
アダコテックでは随時メンバー募集中です!興味があれば一度弊社代表のノートをご確認ください!
Wantedlyやアダコテックのホームページにてエントリーも受付中です!
Discussion