Zenn
🔦

世界一やさしいHLAC入門！(間違い探し編)

2021/08/20に公開
9件
Python
機械学習
画像処理
アダコテック
tech

はじめまして！

2021年4月からAdacotechでエンジニアとして入社しました井上耕太朗です。
それまでは大学にて光学や3次元画像処理、機械学習といった分野の研究に携わっていました。
経歴について詳しくは下記noteの記事にて！
https://note.com/kotaro_inoue/n/nbe941c0a1dfe

技術系の情報はこちらのZennにまとめます。
今回はAdacotechのコア技術であるHLAC(高次局所自己相関)をPythonで実装しながら、サンプル問題として間違い探しを解き、HLACの仕組みについて解説しようと思います。

HLAC: Higher-order Local Auto-Correlation

AdacotechではHLAC特徴量を画像から抽出し、その情報をもとに異常検知を行っています。HLACの訳は高次局所自己相関となり、画像の局所的な自己相関を多次元的に計算することで、ある画像に対する不変特徴量を計算する手法のことです。… オフチョベットしたテフをマブガッドしてリットにするような話に聞こえるかもしれませんが、ブラウザバックはちょっと待ってください！怪しい情報商材のようですが、みなさんはHLACをすでに使いこなしています！

HLAC自体はとてもシンプルであり、使い方さえ分かれば学習枚数が10～100枚程度であってもディープラーニング系技術と同等あるいはそれ以上の検出精度を達成する学習モデルが作成可能です。詳細は弊社ホームページと大津展之先生の論文が参考になります。今回は大津展之先生の「適応学習汎用認識システム:ARGUS」をもとに二値HLAC特徴抽出を実践してみます。

さて、早速やっていきましょうか！…と手を動かすのも良いですが、そのまえにちょっとしたおやつ記事も交えて原理を説明したいと思います。

そもそも相関って？

自己相関…の前にまずは相関から！統計初心者でもご安心、ざっくりと相関とは関連度のことです。日常的な例を挙げると『うだるような暑さの日、かき氷の売上が伸びる』という事象には相関があると言えます。これは我々が『暑い日には冷たいものが食べたくなる』という行動原理があるためです。一方で原理が全く理解できない相関もあります。suprious-correlationsには摩訶不思議な相関がたくさんあり、有名な不思議相関に『ニコラス・ケイジの映画出演数とプールで溺死する人の数』があります。

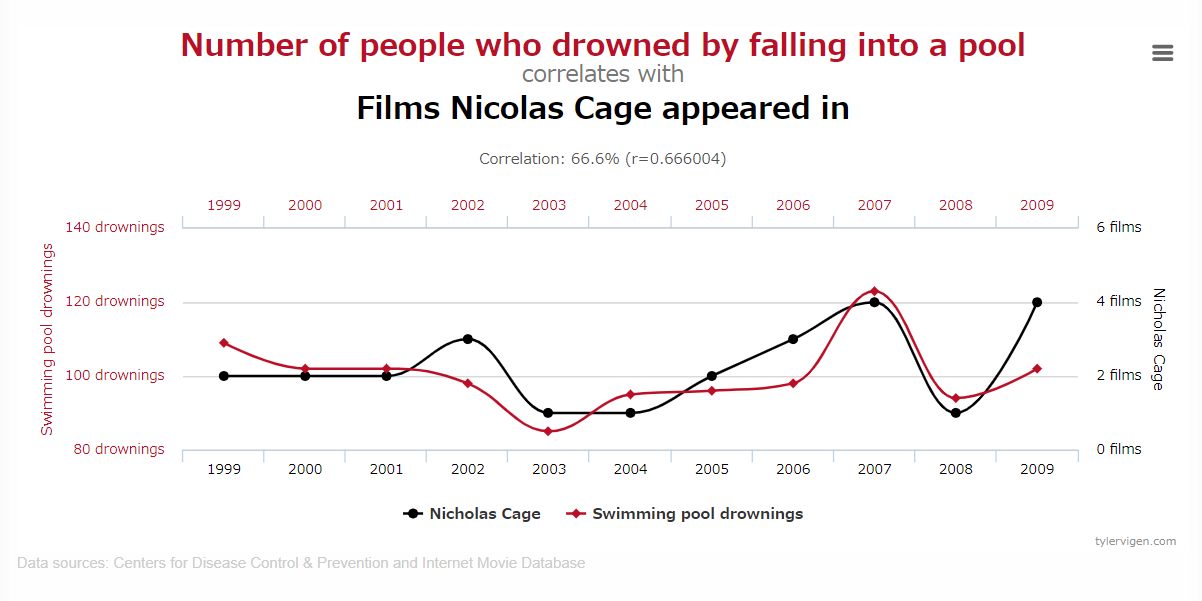
ご覧の通り、グラフだけを見れば結構関連していそうですね！つまり世界にはニコラス・ケイジの映画が出るたびに派手なアクションをプールで真似しようとして亡くなる方が多いのでしょうか？はたまたニコラス・ケイジの映画発表のたびにプールにいたずらを仕掛けるようなカルト的団体が存在するのでしょうか？
答えはどちらも否でしょう。このような相関は疑似相関と呼ばれるもので、偶然の一致により相関が見られる例です。偶然とはいえ、この世には数兆あるいは数京を超える数のデータが存在するので、たった11点のプロット傾向が一致するだけの素っ頓狂な相関は文字通り無数に存在します。

ここで重要なことは、相関は因果関係を一切説明しないということです。『犯罪発生時の被疑者とその24時間以内の水分の摂取確率』、『ライターを日頃持ち歩く人と肺がんの発症率』、『MIT(マサチューセッツ工科大学)に合格する人とパンが主食の人の数』これらの事象はニコラス・ケイジを軽く超える勢いで高い相関を示すでしょうが、いずれも因果を説明してはいません。ちなみに『暑さとかき氷』においても因果を説明しているとは言えません。多くの方は『暑さを和らげるため、暑いとかき氷を食べる』と考えているかもしれませんが、『暑さのせいで冷凍庫の故障率が上がり、中の氷を廃棄するのはもったいないので多少値引きして売る店舗が増え、売上が伸びる』可能性を相関のみで否定することはできないでしょう。国によっては『暑い日にこそ熱いものを摂取する』という文化もあるので、暑さとかき氷の因果を『納涼』と断定するには幾分情報が少なすぎます。

相関の適切な使い方

まったく相関とはなんて信用ならない指標なんだ！ という気持ちになってきたら統計初心者卒業です。これで怪しい情報商材にだまされることも少なくなるでしょう。

相関には大きな落とし穴があることが分かりましたが、落ち込むにはまだ早いです。相関は因果関係を説明しないものの、データの類似度を知るためには非常に有用な指標です。 相関の例では暑さとかき氷のような大きく離れた2つの事象を比較したため、単一の相関で議論をすることはできません。要するに使い方を間違っていたのです。しかし、もともと関係性が明らかな対象同士で相関をとった場合、それは何らかの有用な情報を含んでいることでしょう。

例えばあなたは救急隊員だとします。あるところで緊急事態が発生すると、道端の緊急事態ボタンがポチッと押され、以下のSOS画像情報が無線で救急センターへ届けられるとします。

ただし送受信機器が大変古く、緊急事態の発生するような場所の送信機は濃霧の山中。救急センターまでの距離も遠く、到着するころには電波の息も絶え絶え、以下のようなノイズだらけの画像を受信し続けています。救急隊員であるあなたは、いつやってくるかもわからないSOSシグナルをこのノイズの山から知る必要があります。 実際、以下のGIF画像にはSOSシグナルが入っています。3交代制で8時間この受信機とにらめっこするしかないのでしょうか？これではあなたの脳の緊急事態のほうが実際の緊急事態より早く訪れることでしょう。

しかしこの受信画像とSOS画像情報との間には、まず『画像』というフォーマットにおいて密接な関係があり、おそらくノイズの中にSOS画像情報っぽい傾向がどこかのタイミングで現れることが明らかです。これならSOSシグナルと受信データとの間で相関を計算すると、検出できるのではないでしょうか？やってみましょう！

あるデータXとYがあるとき、その相関\rhoは以下の式で計算できます。

\rho=\frac{\mathrm{cov}(X,Y)}{\sigma_X\sigma_Y}=\frac{平均(Xの平均からの差\times Yの平均からの差)}{Xのばらつき\times Yのばらつき}

一見少し複雑ですが、恐れることはありません。意味さえわかれば単純です。\mathrm{cov}は共分散と呼ばれるものです。共分散とはXとYのそれぞれデータの平均からの差をかけ合わせたもので、要はデータの振れ幅傾向を評価しています。例えばXとYがそれぞれ±1の変動をしたとすると、共分散は以下のように対応します。

X Y 共分散
+1 +1 +1
-1 +1 -1
+1 -1 -1
-1 -1 +1

このように、XとYの数値の増減傾向が一致するときに共分散は1に、また増減傾向が逆のときに-1となります！これが相関の計算における本質的な部分で、分母の\sigma(標準偏差)はXとYのデータの振れ幅の大きさを、上記のような±1に揃えるためのおまけです。これをPythonの関数として書くと以下のようになります。

import numpy as np

def corr(a, b):
    a_m = np.mean(a) # 平均値
    b_m = np.mean(b)
    a_std = np.std(a) # 標準偏差
    b_std = np.std(b)
    return np.mean((a - a_m) * (b - b_m)) / (a_std * b_std)

ではこの関数で相関を計算してプロットしたものがこちら。

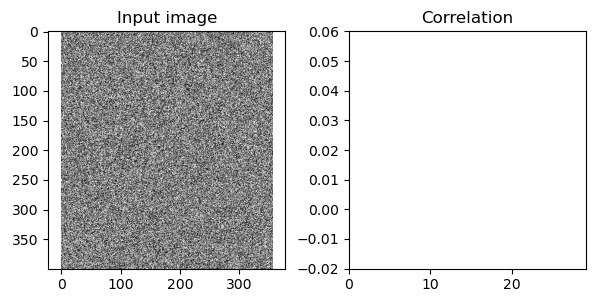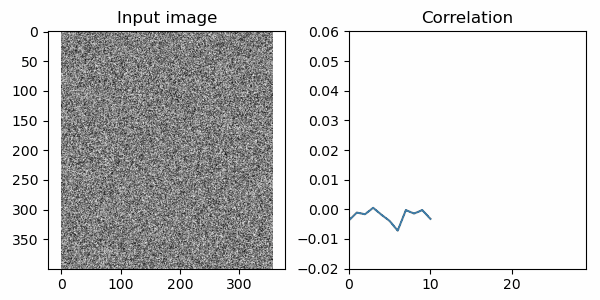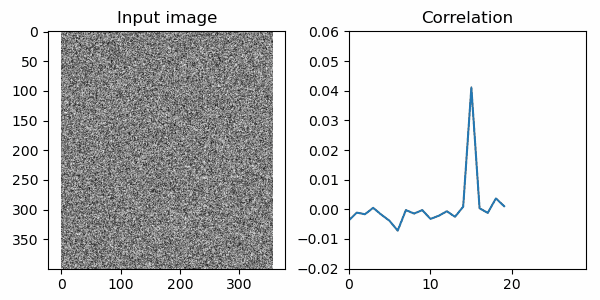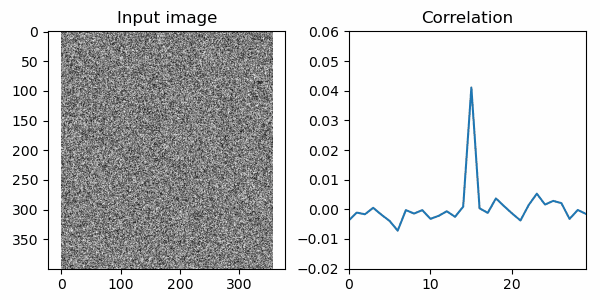
15フレーム目あたりで相関が急に高くなる部分がありますね！事実、15フレーム目の画像にはSOS画像が入力されています。以下に掲載しましたが、言われてみればうっすらと見えるような…？ ともあれ、相関を計算する術を覚えた人類は3交代制8時間の監視業務から開放されるでしょう。めでたしめでたし！

さて、相関は計算したものの、相関には大きく2種類あります。ある対象Aと異なる対象Bとの相関は相互相関と呼ばれます。上記の例も相互相関にあたり、世に出回る情報として多いのもこの相互相関だと思います。一方で、ある対象Aと同じAとの間での相関を自己相関と呼びます。

自己相関と認識

はて、同じ対象同士で相関なんて計算しても、非常に高い相関値しか示さないでしょう。「AはAです。なぜならAはAだからです」みたいな某大臣っぽい話にしかなりません。では自己相関なんてドヤ顔で発表した科学者は耄碌した老人だったのでしょうか？怪しい情報商材を売るために発明されたなんちゃって指標でしょうか？いえいえ、自己相関もまた非常に有用な情報を持っています。

ある対象Aとその全体との比較には全く意味はありません。しかし、比較対象がAの一部を切り取ったものだった場合はどうでしょう？ 例えば自分の身体に対して指で相関をとると、だいたい20箇所に反応する方が多いことでしょう。では目なら？耳なら？髪の毛なら？…と考えていくと、結果として自身におけるある部位によって構成される数となります。そう、これが自己相関です。自己相関とは自身を構成するある一部の要素を数えることなのです。

ところで話が変わりますが、有名なクイズにスフィンクスが旅人に投げかけたといわれる問いがあります。『朝は4本、昼は2本、夜は3本。この生き物とは何か？』 この答えは皆さんご存知でしょうか？答えは『人間』なのですが、これは朝から夜を一生にたとえ、赤子の時分に4本で歩き、成人すれば2本、晩年は杖をついて3本で歩くから、という正直こじつけに無理があろうと思われるクイズです。しかし、このクイズは非常に示唆に富んでいます。では私からのクイズです。『すごく首の長い生き物は何か？』

…

正解はもちろんヤマタノオロチです。えっ、キリンだと思っていましたか？
キリンでも良いですが、どうしてキリンなのでしょう？ヤマタノオロチとの違いは？
このような小賢しい筆者に対し、優しい読者は「ふつう首は1つだし、ヤマタノオロチなんて首8つもあるような伝説上の生き物じゃん！」 と説いてくれるかもしれません。

おやおや！それはHLACではありませんか！！

早くもHLACを使いこなし始めた天才的読者の方に私から言うことはもう何もありません…
え、これ以上の説明が必要ですか？では蛇足だと思いますが、一応書いておきます。

天才的読者であるあなたは、すでにヤマタノオロチとキリンとの間で「首」の自己相関を瞬時に計算し、ヤマタノオロチでは8、キリンでは1という特徴をもとに、生物の首の本数の多くは1本であることから私のメンヘラクイズの不当性を主張しました。これはHLACにおける正常学習に相当します。

だんだん自己相関のすごさが分かってきたのではないでしょうか？私が言いたいことはつまり、様々な要素による自己相関の集まりは認識に相当する ということです。『2本の足があって』、『2本の腕があって』、『非常に大きな脳を1つ持っていて』、『水35ℓ』、『炭素20kg』、『アンモニア4ℓ』、『石灰1.5kg』、『リン800g』、『塩分250ｇ』、『硝石100g』、『イオウ80g』、『フッ素7.5g』、『鉄5g』、『ケイ素3g』、『その他少量の15の元素で構成される生物』というと、我々ホモ・サピエンスである可能性が非常に高いわけです。

画像における認識でも全く同じことが言えます。画像という2次元の行列において、手や足に相当する要素をカウントしていく作業はHLAC特徴量そのものになります。だんだん実装できそうな気がしてきましたね！では二値画像における相関計算用の要素(マスクパターン)は… 偉大なる先人の研究により、3x3ピクセルの範囲での2次特徴までは以下の25種類になります。

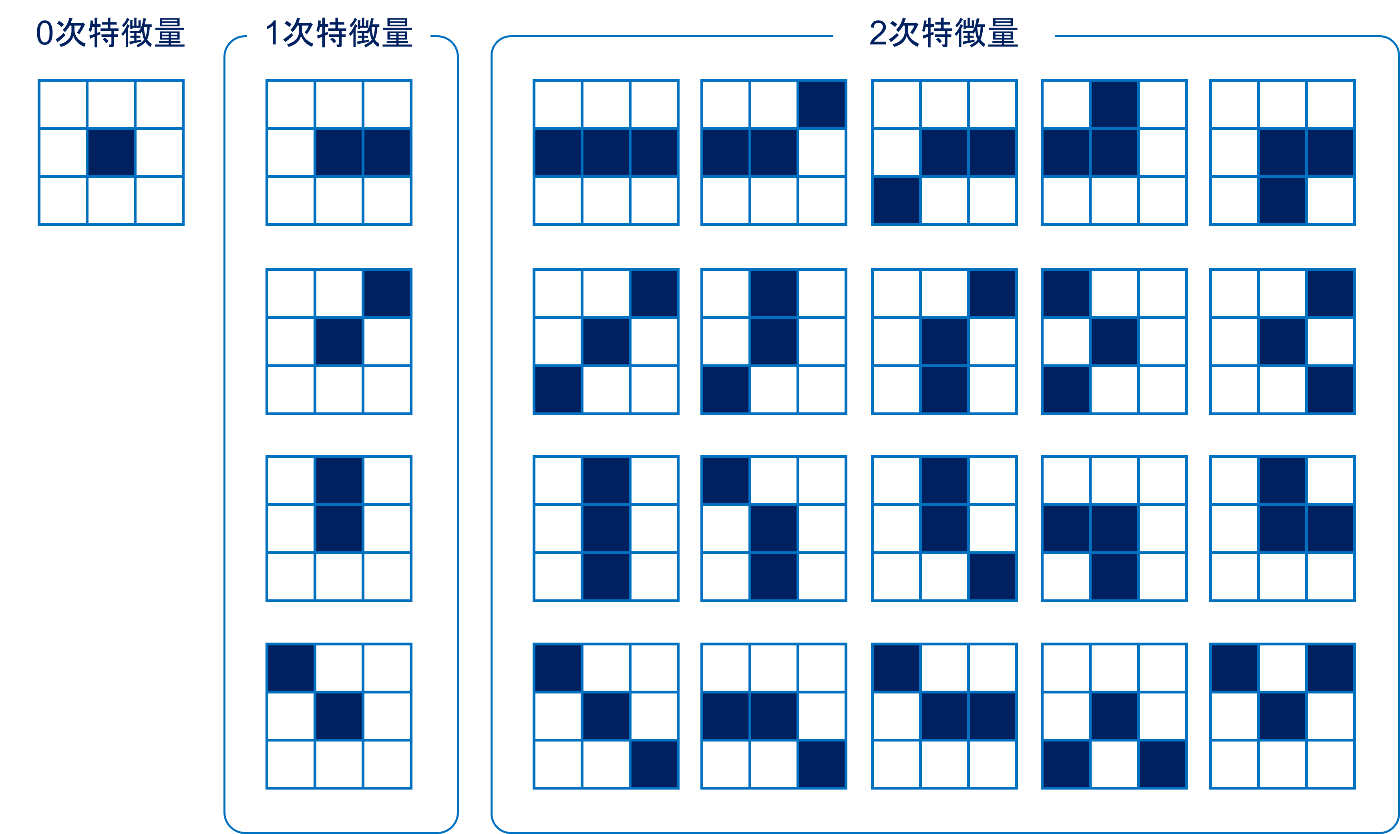
色の濃い部分が輝度で例えるなら1、白い部分が0に相当します。0次や1次といった何やら聞き慣れない言葉が並んでいますが、これは特徴における次元数です。我々の住む世界は4次元(縦・横・奥行き・時間)と言われていますが、0次元では縦も横も無いので点になります。1次元でようやく縦や横という線の概念が発生し、2次では縦と横を同時に表現する面の概念を扱えるようになります。「適応学習汎用認識システム:ARGUS」ではより一般化した形で、N次自己相関関数を計算する以下の式が書かれています。

x(a_1,\dots,a_N)=\int f(r)f(r+a_1)・・・f(r+a_N)dr

ここでxはN次自己相関関数、f(r)はある座標rにおける輝度、そしてa_iはr周辺の相対的な変位です。小難しいことが書いてあるように見えますが、要はあるピクセル周辺の輝度の積和を上記のマスクパターンに従って計算してくだけです。

自己相関は要素数をカウントすることと説明しましたが、これに付随してHALCにはパターン認識における非常にありがたい特性が3つあります。

  1. 位置不変性
    画像内の位置に関わらず、ある対象Aが映る画像には同じHLAC特徴が出ることを意味します。自己相関なので当然といえば当然ですが、場所が変わるたびに別のものと認識するようでは非常に使いづらい指標になってしまうのは想像に難くないと思います。
  2. 加法性
    ある対象AとBが画像内に存在するとき、対象AのHLAC特徴+対象BのHLAC特徴が検出されることを意味します。当たり前のようですが、これが加算によって表現される(独立した特徴量にならない)というのが重要で、対象BのHLAC特徴が既知であれば、対象Aを減算だけで検出できたりするので便利ですね！
  3. 適応学習性
    HLAC特徴量は物体認識や異常検知といったタスクごとに変更する必要がないことを意味します。ディープラーニングではタスクが変わればネットワークモデルの最適化によって抽出すべき特徴が大きく変わる可能性がありますが、その手間が無いので学習および開発プロセスが圧倒的に高速です。

二値HLACを実装してみよう！

ここまで長かったですね！しかしHLACの原理を理解すれば実装はとてもシンプルです。
これから記載するプログラムはGoogle Colabにまとめたので、実行しながら結果を確認したい方は以下からご覧ください。
https://colab.research.google.com/drive/15uImPr5Sp2wwX6hDAAIGCrVSURUoVbYw?usp=sharing

まずは先述した25パターンのマスクを作る必要があるのですが、面倒なので用意しました。

import numpy as np

hlac_filters =  [np.array([[False, False, False], [False,  True, False], [False, False, False]]),  np.array([[False, False, False], [False,  True,  True], [False, False, False]]),  np.array([[False, False,  True], [False,  True, False], [False, False, False]]),  np.array([[False,  True, False], [False,  True, False], [False, False, False]]),  np.array([[ True, False, False], [False,  True, False], [False, False, False]]),  np.array([[False, False, False], [ True,  True,  True], [False, False, False]]),  np.array([[False, False,  True], [False,  True, False], [ True, False, False]]),  np.array([[False,  True, False], [False,  True, False], [False,  True, False]]),  np.array([[ True, False, False], [False,  True, False], [False, False,  True]]),  np.array([[False, False,  True], [ True,  True, False], [False, False, False]]),  np.array([[False,  True, False], [False,  True, False], [ True, False, False]]),  np.array([[ True, False, False], [False,  True, False], [False,  True, False]]),  np.array([[False, False, False], [ True,  True, False], [False, False,  True]]),  np.array([[False, False, False], [False,  True,  True], [ True, False, False]]),  np.array([[False, False,  True], [False,  True, False], [False,  True, False]]),  np.array([[False,  True, False], [False,  True, False], [False, False,  True]]),  np.array([[ True, False, False], [False,  True,  True], [False, False, False]]),  np.array([[False,  True, False], [ True,  True, False], [False, False, False]]),  np.array([[ True, False, False], [False,  True, False], [ True, False, False]]),  np.array([[False, False, False], [ True,  True, False], [False,  True, False]]),  np.array([[False, False, False], [False,  True, False], [ True, False,  True]]),  np.array([[False, False, False], [False,  True,  True], [False,  True, False]]),  np.array([[False, False,  True], [False,  True, False], [False, False,  True]]),  np.array([[False,  True, False], [False,  True,  True], [False, False, False]]),  np.array([[ True, False,  True], [False,  True, False], [False, False, False]])]

hlac_filtersはリストでNumpyの2次元行列で表現された2値マスクパターンを格納しています。あとは画像内にこのマスクパターンがそれぞれ何個存在するかをカウントすれば2値HLAC特徴量になります。これはどのように実装すると楽そうでしょうか？画像の左上から右下まで同じフィルター処理… というところでピンと来る方はいるかもしれませんが、これは畳み込みで簡単に実現できます。畳み込みについては数式より以下のアニメーションを見るだけで理解できると思います。


2次元畳み込み 引用元: https://github.com/vdumoulin/conv_arithmetic

本質的な部分はもうこれで全てで、あとは各マスクで畳み込み→マスクと一致する数を集計で終了です。Python実装は以下のようになります。

from scipy import signal

def extract_hlac(image, hlac_filters):
    result = []
    image = np.uint8(image)
    hlac_filters = np.uint8(hlac_filters)
    for filter in hlac_filters:
        feature_map = signal.convolve2d(image, filter, mode='valid')
        count = np.sum(feature_map == np.sum(filter)) # マスクと一致する数を集計
        result.append(count)
    return result

2値HLACですが、Scipyのcovolve2dはBool(2値)を扱えないようなので、8bitのグレイスケール空間に変換する必要がある点には注意してください。また、畳み込みには画像の周辺部分の計算の仕方が複数あり、デフォルトでは画像をゼロパディング(周囲を0で埋める)して計算します。多くの画像処理はそれで問題ないのですが、HLACでは計算誤差に相当するため、mode='valid'でゼロパディングを無効化しています。

ではこの関数を使って、実際に2値HLACを計算してみます。
今回は下記の4種類の画像を用意しました。この画像を使って位置不変性や加法性を確認してみましょう。
(実際に計算してみたい方は右クリックから画像の保存でダウンロードしてください。)

いぬ(dog1.png) 場所の違ういぬ(dog2.png)
ねこ(cat.png) いぬとねこ(merge.png)

位置不変性の確認

まずは犬のHLAC特徴量を計算してみましょう！流れとしては以下のようになります。

  1. 画像をグレイスケールで読み込み
  2. 画像を2値化する
  3. HLAC特徴量を計算する

Pythonで書くとこんな雰囲気です。今回は2値化の閾値は適当に127としました。

import cv2
dog1 = cv2.imread('./dog1.png', cv2.IMREAD_GRAYSCALE) > 127
dog1_hlac = extract_hlac(dog1, hlac_filters)

いぬのHLAC特徴量をmatplotlibで可視化してみると…

import matplotlib.pyplot as plt
plt.plot(dog1_hlac)
plt.show()


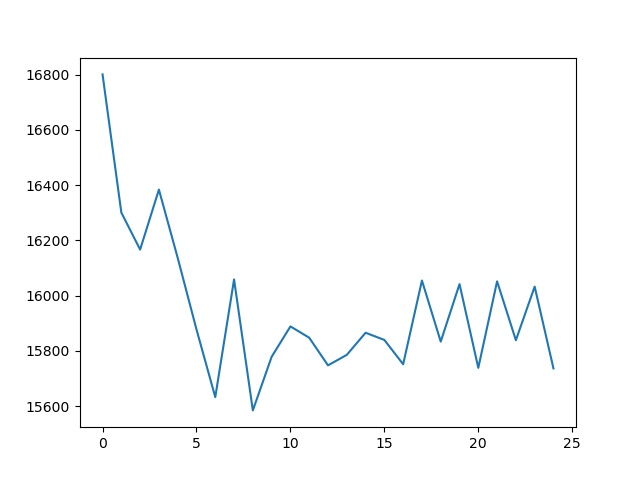
いぬのHLAC特徴量

このようになります！このグラフの見方は、横軸がマスクパターンの種類、縦軸が画像内に存在するマスクパターンの数になります。HLACでは25個の要素に分解してグラフのような要素で犬を表現できることがわかりました。
では、位置ずれをしているdog2.pngにも同じ処理をして比較してみましょう！

dog2 = cv2.imread('./dog2.png', cv2.IMREAD_GRAYSCALE) > 127
dog2_hlac = extract_hlac(dog2, hlac_filters)

plt.plot(dog1_hlac, label='Dog1')
plt.plot(dog2_hlac, label='Dog2')
plt.legend()
plt.show()

上記のコードで出力したグラフが以下のようになります。


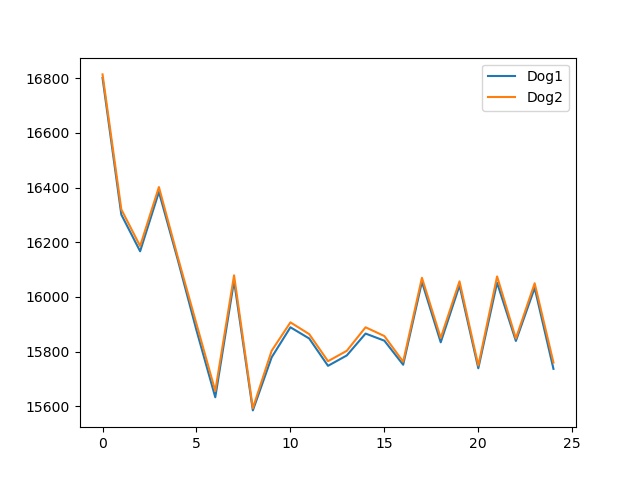
位置ずれのある犬のHLAC特徴量の比較

画像化する段階でわずかな違いがあるものの、傾向は完全一致することが分かると思います。これがHLAC特徴量の位置不変性です。

加法性の確認

この調子でねこのHLAC特徴量も計算してみましょう。

cat = cv2.imread('./cat.png', cv2.IMREAD_GRAYSCALE) > 127
cat_hlac = extract_hlac(cat, hlac_filters)

plt.plot(cat_hlac)
plt.show()


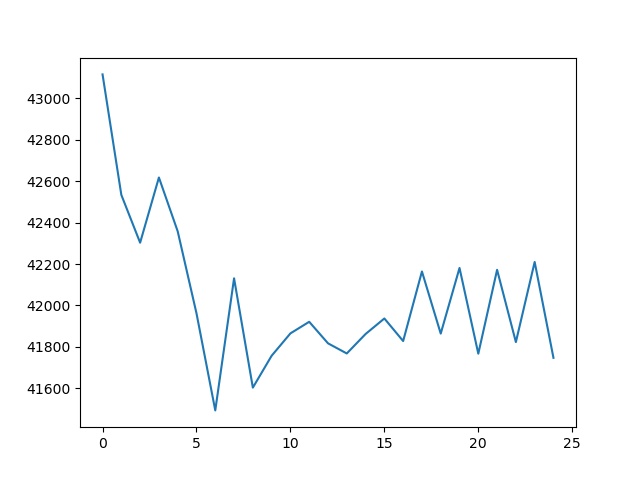
ねこのHLAC特徴量

なるほど、マスク6と8のカウントなどを見ると、少しいぬとは傾向が違うようです。
ではいぬとねこのいる画像ではどうでしょうか？

merge = cv2.imread('./merge.png', cv2.IMREAD_GRAYSCALE) > 127
merge_hlac = extract_hlac(merge, hlac_filters)

plt.plot(cat_hlac)
plt.show()


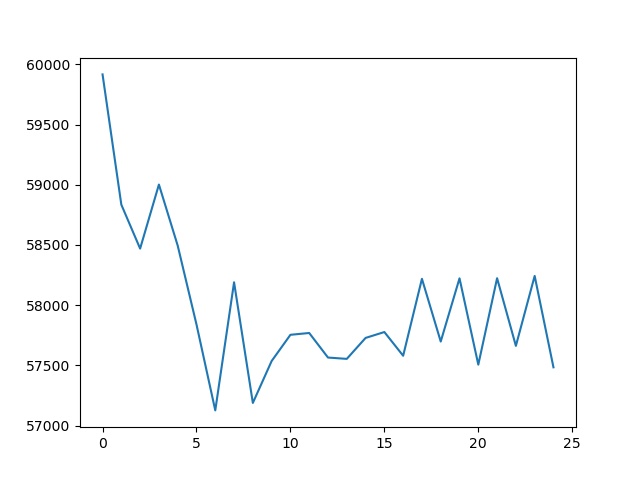
いぬとねこのHLAC特徴量

ではいよいよ加法性を検証するときです！
いぬ&ねこHLACからいぬのHLAC特徴を引いてみましょう。

print("Cat HLAC")
print(cat_hlac)
print("DogCat HLAC - Dog HLAC = Cat HLAC?")
print(list(np.array(merge_hlac)-np.array(dog1_hlac)))

以下にプログラムの出力を示します。

Cat HLAC
[43116, 42534, 42303, 42618, 42358, 41962, 41493, 42131, 41603, 41757, 41865, 41921, 41817, 41768, 41862, 41937, 41828, 42164, 41864, 42181, 41767, 42172, 41823, 42210, 41747]

DogCat HLAC - Dog HLAC = Cat HLAC?
[43116, 42534, 42303, 42618, 42358, 41962, 41493, 42131, 41603, 41757, 41865, 41921, 41817, 41768, 41862, 41937, 41828, 42164, 41864, 42181, 41767, 42172, 41823, 42210, 41747]

ちゃんと一致していますね！これがHLACの加法性です。

HLACで間違い探し

もうHLACの実装は終わったので、あとは消化試合です！
ColabではWikipediaの間違い探しの画像を使用しているので、追認したい方は上記の画像をダウンロードするか、Colabのコピーを作成し、自分で動かしてみてください。

さて、今回HLACで解いてみるのは間違い探しです！これをパソコンに解いてもらいましょう。
画像をダウンロードした後は、とりあえず計算しやすいよう中央で分割します。

image = cv2.imread('Spot_the_difference.png')
r,c = image.shape[:2]
reference = image[:,:int(c/2)]
target = image[:,int(c/2):]

fig = plt.figure()
ax = fig.add_subplot(1,2,1)
ax.set_title('Reference')
plt.imshow(reference[:,:,::-1])
ax = fig.add_subplot(1,2,2)
ax.set_title('Target')
plt.imshow(target[:,:,::-1])
plt.show()

以下が実行結果です。全部で15箇所の違いがあるようですが分かるでしょうか？

左右で分割した間違い探し画像

さて、これをHLAC特徴量で比較するわけですが、全体で計算してしまうと、どの部分で特徴量に大きな違いが発生するかわかりません。ここはいくつかのパッチに画像を分割し、それぞれのHLAC特徴量を計算してみるのが簡単な解決策です。サクッと実装してみましょう。

# パッチ版HLAC特徴量
def split_into_batches(image, nx, ny):
    batches = []
    for y_batches in np.array_split(image, ny, axis=0):
        for x_batches in np.array_split(y_batches, nx, axis=1):
            batches.append(x_batches)
    return batches

def extract_batchwise_hlac(image, hlac_filters, nx, ny):
    batches = split_into_batches(np.uint8(image), nx, ny)
    hlac_filters = np.uint8(hlac_filters)
    hlac_batches = []
    extracter = lambda args: np.sum(signal.convolve2d(args[0], args[1], mode='valid') == np.sum(args[1]))
    with ThreadPoolExecutor(max_workers=int(os.cpu_count() / 2)) as e:
        for batch in batches:
            result = list(e.map(extracter, zip([batch] * len(hlac_filters), hlac_filters)))
            hlac_batches.append(result)
    return np.array(hlac_batches)

やっていることは以前と変わりません。ただ特徴抽出前に画像をパッチに分割し、それをマルチスレッドで特徴抽出するような構成になっています。

では、とりあえず縦横20分割、つまり計400個のパッチになるよう分割して計算してみると…

nx, ny = 20, 20
reference_bin = cv2.threshold(cv2.cvtColor(reference, cv2.COLOR_BGR2GRAY), 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)[1] == 255
target_bin = cv2.threshold(cv2.cvtColor(target, cv2.COLOR_BGR2GRAY), 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)[1] == 255
reference_hlac = extract_batchwise_hlac(reference_bin, hlac_filters, nx, ny)
target_hlac = extract_batchwise_hlac(target_bin, hlac_filters, nx, ny)

fig = plt.figure()
ax = fig.add_subplot(1,3,1)
ax.set_title('Reference')
plt.imshow(reference_hlac, aspect='auto', cmap='gray')
ax = fig.add_subplot(1,3,2)
ax.set_title('Target')
plt.imshow(target_hlac, aspect='auto', cmap='gray')
ax = fig.add_subplot(1,3,3)
ax.set_title('Difference')
plt.imshow(target_hlac-reference_hlac, aspect='auto', cmap='gray')
fig.tight_layout()
plt.show()

今回は画像の2値化にあたり、ちょっと高級な閾値決めをしていますが、それ以外は全く変わりありません。出力は以下に示しましたが、一行一行があるパッチにおける25個の成分で表されるHLAC特徴量を可視化しています。右に示したHLAC差分特徴量を見ると、どのパッチで傾向が違うのか可視化されていますね！


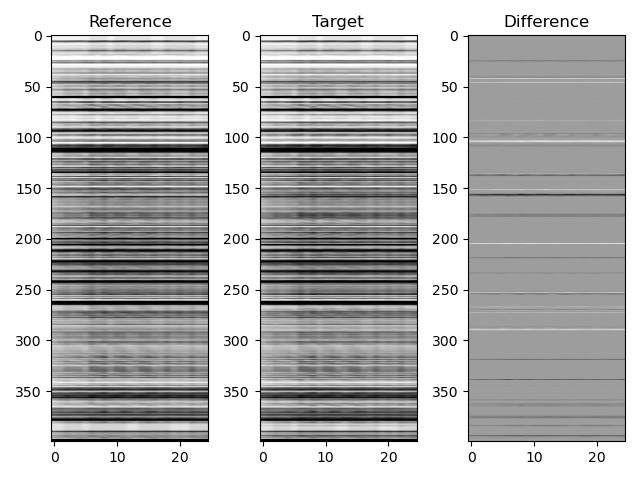
パッチ単位HLAC特徴量の比較

しかし、このままではどのパッチがHLAC特徴で違うのか定量評価しづらいです。HLAC特徴量は25次元のベクトルであるので、長さを揃えた2つのベクトル間の内積を計算することで角度差に変換できます。やってみましょう！

def vector_angle(hv1, hv2, eps = 1e-6):
    hv1 = (hv1 + eps) / np.linalg.norm(hv1 + eps) # ベクトルの長さを揃える
    hv2 = (hv2 + eps) / np.linalg.norm(hv2 + eps)
    return np.arccos(np.clip(np.dot(hv1, hv2), -1.0, 1.0))

この角度差の可視化は以下のようにできます。

hlac_angles = [vector_angle(rv, tv) for rv, tv in zip(reference_hlac, target_hlac)]
plt.plot(hlac_angles)
plt.show()

コサインを計算したので、内積が完全一致する場合は0、ベクトル間の差に従い角度は大きくなります。

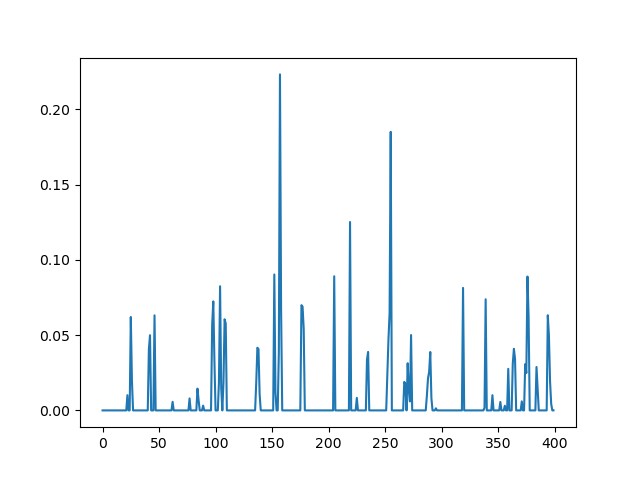
パッチ間のHLAC特徴量差の角度による可視化

ようやくこれでReference画像と異なる部分を判定できそうですね！パッチ分割したのでそれらの情報を元の画像ベースに戻してあげる必要がありますが、こちらは単に地道な作業なので以下の関数にまとめました。

def visualize(image, hlac_angles, nx, ny, th=0.1):
    batches = split_into_batches(image, nx, ny)
    dst = np.zeros_like(image)
    hlac_angles -= np.nanmin(hlac_angles)
    hlac_angles /= np.nanmax(hlac_angles)
    py = 0
    for y in range(ny):
        px = 0
        for x in range(nx):
            batch = batches[y * nx + x]
            angle = hlac_angles[y * nx + x]
            if angle > th:
                dst = cv2.rectangle(dst, (px, py), (px + batch.shape[1], py + batch.shape[0]), (0, int(255 * angle), 0), -1)
                dst = cv2.rectangle(dst, (px, py), (px + batch.shape[1], py + batch.shape[0]), (0, 255, 0), 1)
            px += batch.shape[1]
        py += batch.shape[0]
    return cv2.addWeighted(image, 0.2, dst, 0.8, 1.0)

内容としてはパッチごとの角度差を正規化(0～1の幅に揃える)し、ある閾値を超えるものだけ色付けするという内容になります。この関数を使うと…

out = visualize(reference, hlac_angles, nx, ny)
plt.imshow(out[:, :, ::-1])
plt.show()


HLAC特徴量差が大きい部分の可視化画像

このようにHLAC特徴量で差が大きい部分を可視化できます！
可視化の緑輝度は特徴量差にそのまま対応しているので、HLAC特徴が特に異なる部分は明るい緑色になっています。
一応この画像をもとにWikipediaに示されている15箇所を確認しましたが、すべて色づいていることを確認しました。

まとめ: HLACとは何だったのか

いかがだったでしょうか！
今回は私自身も勉強中の身ではありますが、HLACについて解説してみました。
この記事を読んで以下のことが理解できれば満点だと思います。

  • 自己相関とは自身の中の一部の要素数をカウントすること
  • あらゆる要素の自己相関の集まりは『認識』とほぼ等価
  • HLACは画像内のあるパターンの要素をカウントすることで特徴量へ変換する

HLACに限らず、自己相関は日常的にありとあらゆる場所に応用されています。
この記事で自己相関という武器を身につけ、みなさんの日常業務の助けとなれば幸いです！

メンバー募集中です！

HLACを活用した事業に興味が出てきましたか？であれば一度弊社代表のノートをご確認ください！
https://note.com/ryotakawamura9/n/na049bc517d96

Wantedlyにてエントリーも受付中です！
https://www.wantedly.com/companies/company_8396481/projects

Discussion

MiMi

大変おもしろい技術ですね。この技術は商用利用可能なのですか？それとも特許料とか必要なんでしょうか？
商用利用予定はないのですが、面白そうなので内容の調査をしてみたい→役に立つものをつくってみたいと思いご質問させていただきました

Kotaro InoueKotaro Inoue

ご覧いただきありがとうございます！
商用利用は可能ですが、利用方法次第では産業技術総合研究所(産総研)に特許使用料を収める必要があります。商用利用される際は具体的な利用方法が定まり次第、一度産総研の知的財産部にご相談されたほうが賢明かと思います。手元で試してみる限りそういった制約はないので、色々なことへの応用にチャレンジしていただければと思います！

MiMi

お返事ありがとうございます。まずはHLACの調査をしてみたいと思います。
対象物の向きが違うのをどうしたらいいのかで悩んでいるので進むか微妙ですが(^_^;)

zanjibarzanjibar

コンクリートをハンマーで 叩く音には適用できるんでしょうか

Kotaro InoueKotaro Inoue

どのような用途でご利用になるか次第だとは思いますが、音も2次元(x軸に時間、y軸に振幅やx軸に周波数,y軸に音圧)で表されるような表現であればHLAC特徴量による表現が可能です。(音の自己相関であればフーリエ変換もその一種であり、より適しているかもしれませんが)

仮にHLAC特徴量を用いてコンクリートをハンマーで叩く音をパターン認識したい場合を想定すると、音の場合は局所的だけでなく大域的な特徴を取る必要もあるので、相関幅という工夫が必要になるかもしれません。

zanjibarzanjibar

音はむずかしいのでｗ簡単なグラフのあたりから行きたいと思います

Kotaro InoueKotaro Inoue

私の知る範囲では、時刻データベースへの直接的な応用事例はありません。
HLACは基本的に2次元の行列に対する自己相関を求める特徴なので、単純な1次元の時系列データであればカルマンフィルタであったり、自己回帰を用いた検知手法が有効と思います。
ただし、時系列データにおいても2～3カラムにまたがる情報の関連性を特徴量化したい、あるいは動画のような時系列画像において異常検出したい場合、HLACのような特徴を算出することで何らかの示唆が得られるかもしれません。

zanjibarzanjibar

カラム数は、最大１０万なので使えそうと思いました。