ワンオペの限界っ!アンサンブルモデル入門!
これまでのお話
これまではHLACの特徴抽出に始まり、良品学習によるモデル構築までのお話を書いてきました。
今回はさらにその続きで、運用面を考えたモデル組み合わせのお話です!
存在しない『最適』
みなさんは解決が困難な問題と立ち向かうとき、どうするでしょうか?レベル上げでしょうか?個人の能力不足によって解決できない問題、たとえば100kgのバーベルを持ち上げる、TOEICで100点ピタリ賞を狙う程度であれば、鍛錬や勉強といったレベル上げで対処も可能でしょう。ただし世の中には個の能力の向上だけでは如何ともし難い課題が存在します。
例えば横綱級力士はほぼ確実に競馬で騎手として勝つことはできないでしょう。
逆に騎手として一流の方であったとしても春場所は惨敗するでしょう。
何を当然のことを思うかもしれませんが、正にこれが問題なのです!

重力魔法で馬に乗る力士と圧倒的体幹で張り手を躱す騎手はファンタジー
力士と騎手はそれぞれ種族は人間(ホモ・サピエンス)ですが、その成長過程で
- 力士は相撲性能を最大化
- 騎手は騎馬性能を最大化
した人間と考えられ、この境遇は同じアルゴリズムでありながら最適化された問題だけが異なる機械学習モデルと同等と言えます。言えるんですえぇ。 力士モデルは当然相撲界では無類の性能を発揮しますが、競馬に出たところで体重そして騎馬経験の不足から当然勝つことはできません。騎手モデルは騎馬性能を最大化するために極力体重や身長を落とした結果、やはり春場所は惨敗します。ここで大切なことは「相撲」と「競馬」という2つの問題に対して最適化した結果、それぞれの性能がトレードオフ(二律背反)関係にあるということです。
みなさんも生きていれば一度は競馬と相撲で両方強いスーパースターの誕生を夢見たことがあると思いますが、これはなかなか難しいことは直感的に理解いただけると思います。しかし機械学習モデルを作る上ではそれが目に見えないあまり、ある2つの課題がトレードオフにあることに気づかず、2つの課題を同時に解決できるようなスーパースターを見つけようと四苦八苦してしまうことがあります。
モデルを組織管理(アンサンブル)する時代の到来
会社や社会といった枠組みでもそうですが、高度に分業化の進んだ現代、様々な専門技能によって達成される業務の全てを1人の人間がカバーすることは困難であり、たとえ牛丼一杯の提供であろうと、待ち行列管理、調理、計量、提供、レジと様々な技能が要求されます。機械学習で解く必要のある問題も導入背景からして高度であることが多く、機械学習にもアンサンブル(ensebmle)という分業化のような概念が導入され始めました。
アンサンブルとは音楽用語で2人以上が同時に演奏することのようですが、機械学習におけるアンサンブル学習も2つ以上のモデルを組み合わせて作ることが前提となります。しかし音楽であれば美しいハーモニーを聞けば良い楽器や歌手の組み合わせがわかるものの、機械学習モデルとなるとなかなか難しそうです。そう、アンサンブルの難しさはどうやって複数の機械学習モデルをいい感じに組み合わせるのか? という組み合わせ最適化の問題なのです。
先程の競馬と相撲の例では各々の競技性が既知であるため、どちらの競技でも強い選手を作ることの筋の悪さが明らかでしたが、現実の問題はそう簡単に割り切れるものではありません。そこでなんと偉い先人たちは実験的にそれらを見定める方法を考えました。それらは大きく3つに分けられます。
- とりあえず大量のモデルで多数決をして予測 (バギング)
- 難しい問題だけを再学習して予測 (ブースティング)
- 様々な学習済みモデルを運用するモデルを用意して予測 (ブレンディング/スタッキング)
この記事で着目するのは主に3つ目の運用なのですが、これらの簡単な概要を少し解説します。
手法1: とりあえず大量に作って多数決(バギング)
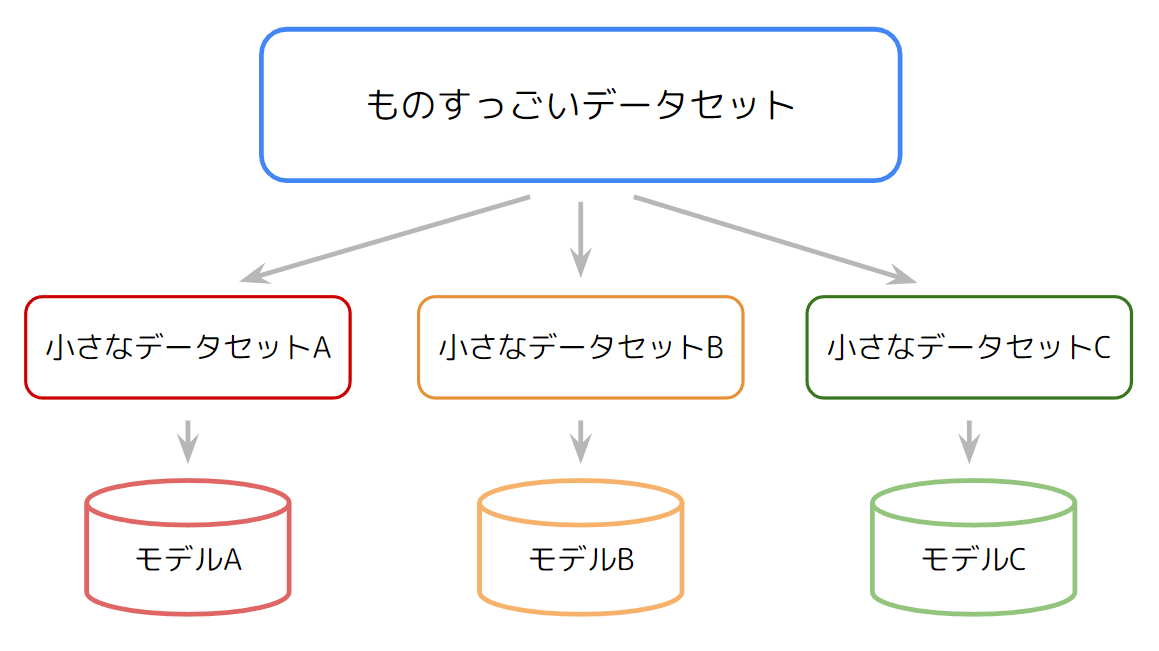
究極的な精度の追求よりモデルの作成しやすさや予測の安定度から好まれることの多いアンサンブル手法で、1つの大きなデータセットを機械的にN個に分割し(データは一部重複しても良く、ブートストラップサンプリングと呼ばれます)、N個のモデルによる予測値の平均であったり最多投票によって最終結果を出力します。ちなみにものすごいバグを起こしそうなこのバギング(bagging)の語源はbootstrap+aggregatingと、無理矢理感が半端ねぇワードの組み合わせです。
それぞれのモデルは小さな部分問題を解くため、データの母集団が何らかの混合分布的なものである場合、微妙に特性が異なるモデルを多数作ることができます。うまくフィットすれば専門家会議的な状態になりますが、失敗すれば烏合の衆ができあがる構成でもあります。機械学習アルゴリズムの大御所の一つでもあるランダムフォレストがこの手法を改良したもので今日でも盛んに利用されています。
手法2: 難しい問題を分割して学習 (ブースティング)
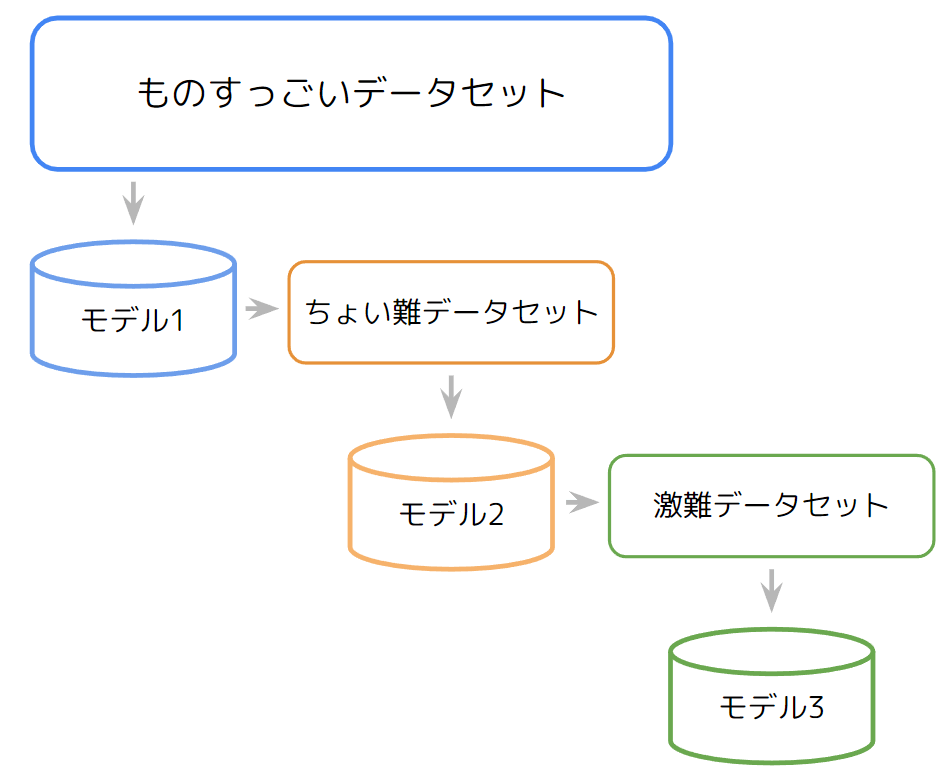
ロケットのブースターのようにモデルを多段連結させる方法で、ある1つのデータセットに対し1つのモデルを作り、そのモデルが誤答したものを次のモデルに学習させるというワガママボディを作り上げるアンサンブルモデルです。2つ目以降のモデルは1段前のモデルが確定しないと学習できないため、先程のバギングと異なり最適化時間が長くなる傾向にあります。
後段のモデルになるほど難しいタスクをこなすことが多く、一般的な人が解決できない問題を専門家レベルを上げながら調査するようなイメージなので、バギングよりは人間の直感的にも理解しやすい気がします。ブースティングは近年大人気の手法で、MicrosoftのLightGBMが決定木ベースの手法でよく利用されている印象です。
手法3: 予測モデルから予測モデルを学習 (ブレンディング/スタッキング)
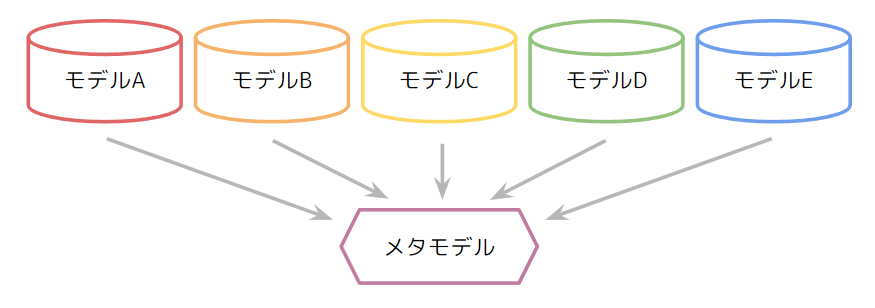
ブレンディング/スタッキングは手法1や2によってモデル候補ができた後、それらの指揮官を用意するような手法です。たとえばあなたが美味しい料理の作り方を誰かに聞くとして、フランス料理人と中華料理人の友人がいれば、チャーハンであれば中華料理人、ポタージュであればフランス料理人と聞く人を変えるのは自然なことと思います。ブレンディングやスタッキングも同様のコンセプトで、問題に応じて適切なモデルをアサインするモデルを配置することでさらに精度を高めることができます。一般的にこの指揮官的な立場のモデルは人間ライクな思考を定量化しているとも捉えられるので、メタモデルと呼ばれます。
ブレンディングとスタッキングの境界はやや曖昧なようですが、ブレンディングは上記をワンセットの状態とし、スタッキングはそのセットを数珠つなぎするような構成を指すことが多いようです。
モデルアンサンブルをやってみよう!
さて、上記までの情報はネットの海を漁ればいくらでも出てくる情報です。
ここからはより実践的な内容として、モデル評価方法からアンサンブルモデルの作り方を解説します!今回はサンプル例として、ある画像の2値分類にチャレンジしてみます。2値分類とは2つのグループに分けることで、我々の業界でいくと良品と不良品を選別するようなイメージです。今回のモデルケースとしては画像になりますが、最終的に数値データ化できる対象であれば何でも良いです。
実験環境としてはGoogle Colabがおすすめです!
下記にサンプルプログラムは全て保存したので動かしながらご確認ください。
モデルを評価する
アンサンブルの前にモデルの精度を評価できなければ改善も何もありません。
そこで2値分類問題に対して最も一般的なKPIとなりうるROCカーブとAUCを紹介します!
サンプルデータ(モデル)を生成する
なにはともあれデータが必要です。まずはサンプルデータを生成しましょう。
今回は画像の二値分類という体でOKとNGの2つの正規分布からそれぞれ50個のデータをサンプリングします。正規分布とはざっくりとこの世の多くの事象が従う確率分布のことで、こういったシミュレーションにはうってつけの分布です。
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(1)
ok_score = np.random.normal(1, 0.3, 50) # 平均1 分散0.3の正規分布乱数を50個生成
ng_score = np.random.normal(2, 0.5, 50) # 平均2 分散0.5の正規分布乱数を50個生成
このコードから出てくるOKとNGの分布をヒストグラム(横軸を画像に対応するスコア、縦軸をその数で示すプロット)で描画してみると……
plt.hist([ok_score, ng_score], bins=25, color=['blue', 'red'], alpha=0.7, label=['OK','NG'])
plt.legend()
plt.show()

このように2つの分布が微妙に分かれた状態が見れます!
この2つの分布がしっかり分かれているほど判別モデルの性能としては良いということが言えますが、この分布を見て一体どの程度分かれているというべきなのでしょうか?
ここで判別モデルの性能の評価の定番、ROCカーブが登場します!
ROCカーブ
ROC(Receiver Operatiorating Characteristic)カーブとは受信者操作特性なんて日本語もありますが、機械学習界隈では「あーるおーしーカーブ」が通称かと思います。ROCカーブは先程の2つの分布からいろいろな場所で閾値を設定して
- 縦軸にTrue Positive Rate(真陽性率): 閾値以上のNGスコアの割合、検出率ともいう
- 横軸にFalse Positive Rate(偽陽性率): 閾値以上のOKスコアの割合、過検出率ともいう
をプロットしたカーブです。要するに閾値を下げながら検出率を上げていったときに、どの程度ポカミス(過検出率)の割合が増えるのか? をプロットしたものがROCカーブです。
実際これは百聞は一見にしかずなので、下の動画を見ていただきましょう。

左側がヒストグラム、そして右側がROCカーブ、緑の点線はヒストグラムにおいては閾値、ROCカーブにおいては閾値を設定したときの過検出率を示します。
ROCカーブの見方ですが、
- 最初のプロットでは90%ほどまで一気に検出率(縦軸)が上昇し、その時点での過検出率(横軸)は0の位置に存在
- そして次第に検出率が高くなるほど過検出率も高くなっていき、検出率が1に到達する時点では過検出率が約0.45の位置に存在
よってROCカーブさえ見れば、NGの約90%は無損失で検出可能で、NGを全て検出したい場合は約45%の過検出が発生することが一目瞭然なのです!
これは大変便利で、モデルの性能はこのROCカーブがなるべく左上に張り付くほど良いという指標となります。実際に以下2つの場合を比べてみましょう。
・分布の分離度が高い場合
np.random.seed(1)
ok_score = np.random.normal(1, 0.3, 50)
ng_score = np.random.normal(2.5, 0.5, 50)
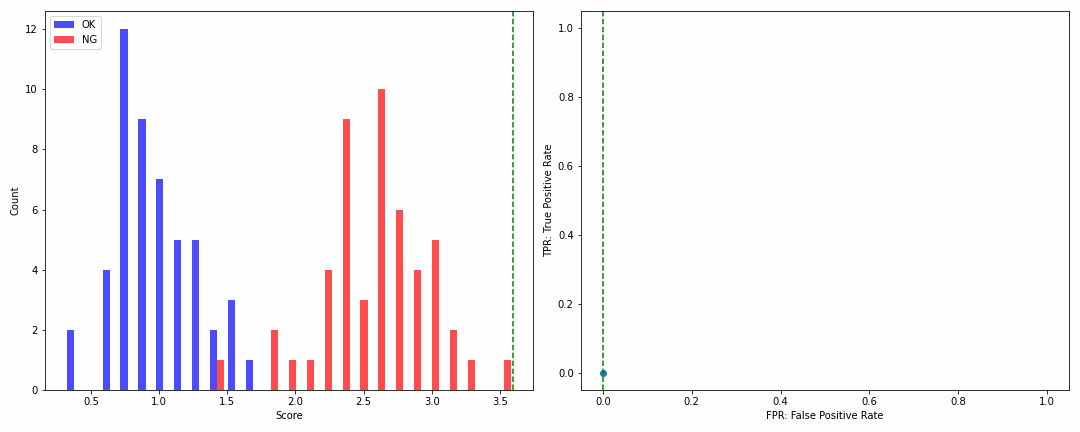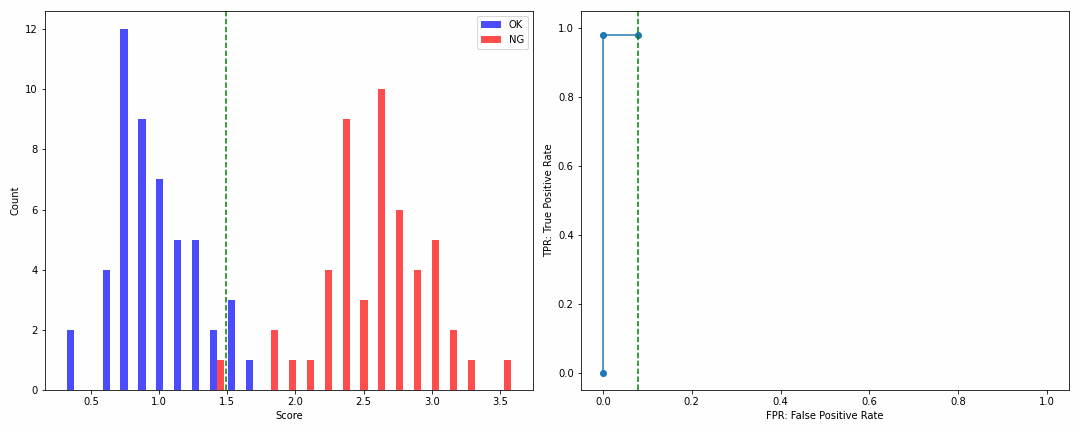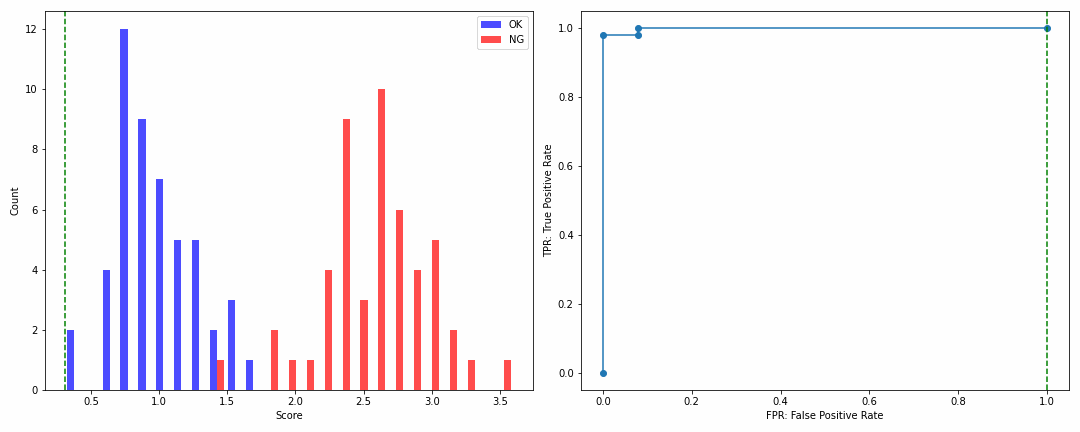
・分布の分離度が低い場合
np.random.seed(1)
ok_score = np.random.normal(1, 0.3, 50)
ng_score = np.random.normal(1.5, 0.5, 50)
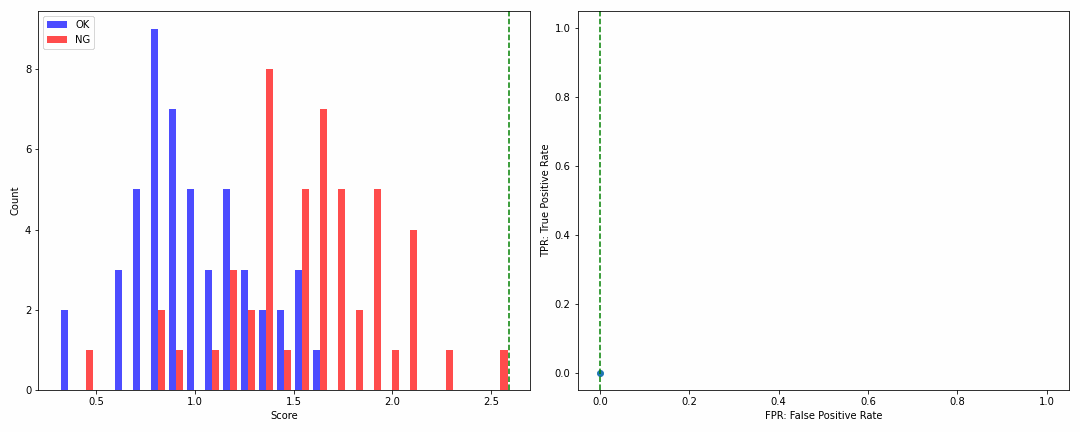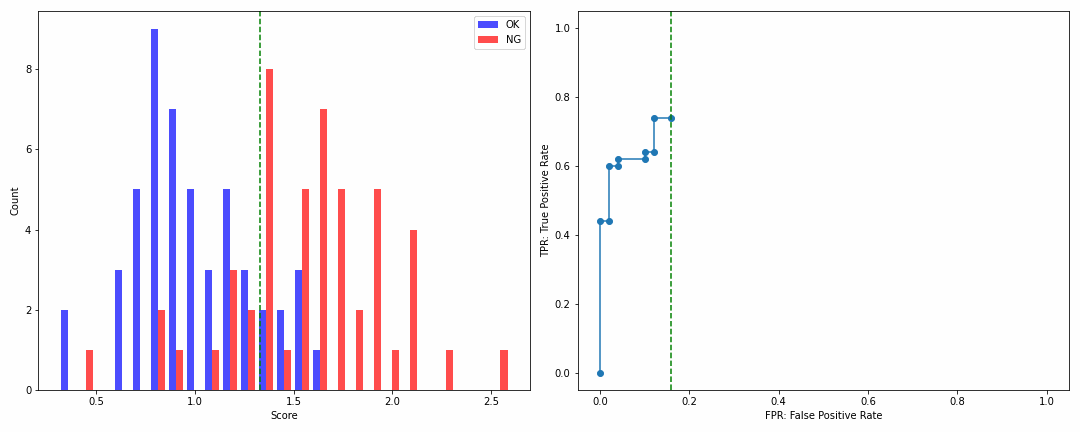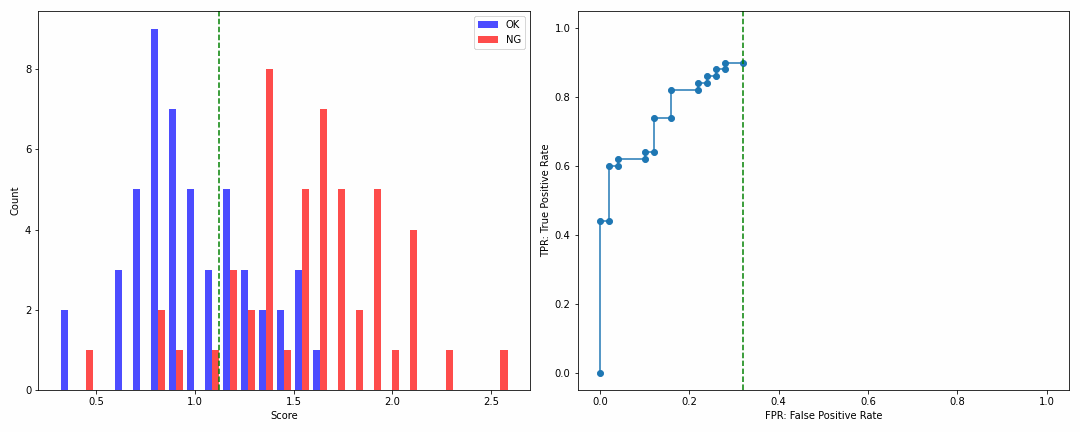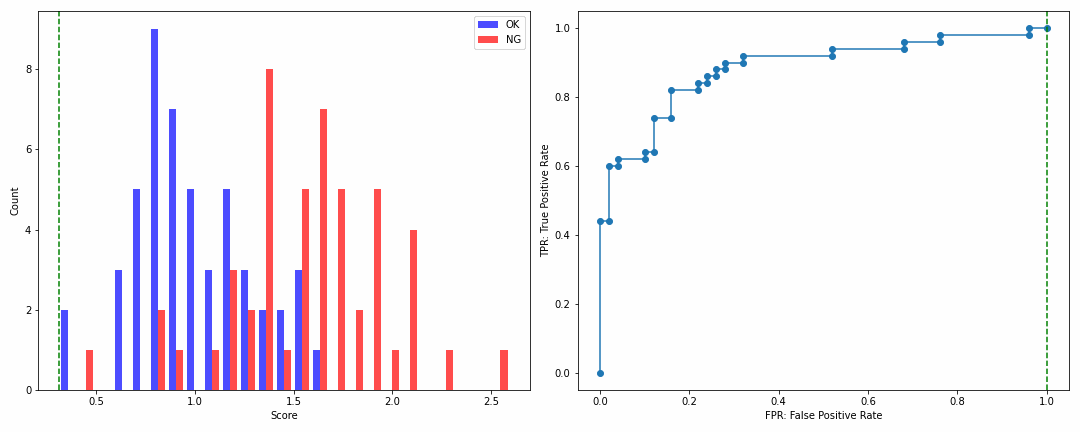
ROCカーブの角のカケ具合でモデル性能が一目瞭然ですね!
ちなみにROCカーブの描画はなかなか大変そうですが、Scikit-learnという便利パッケージを使えば一瞬で描画できます。
from sklearn.metrics import roc_curve
ground_truth = [0]*len(ok_score)+[1]*len(ng_score)
fpr, tpr, thresholds = roc_curve(ground_truth, np.concatenate([ok_score, ng_score]))
plt.plot(fpr, tpr, marker='o')
plt.show()
ROCカーブ描画のスクラッチ実装
fpr = [0]
tpr = [0]
thresholds = np.sort(ng_score)[::-1]
thresholds = thresholds[np.argmax(thresholds<=ok_score.max())-1:]
for score in thresholds:
fp = np.sum(ok_score>score)
tp = np.sum(ng_score>score)
if fp != fpr[-1]: # FalsePositiveが増えた場合はステップ状に更新する
fpr.append(fpr[-1])
tpr.append(tp)
fpr.append(fp)
tpr.append(tp)
fpr.append(fpr[-1])
tpr.append(len(ng_score))
fpr.append(len(ok_score))
tpr.append(len(ng_score))
fpr = np.array(fpr)/len(ok_score)
tpr = np.array(tpr)/len(ng_score)
plt.plot(fpr, tpr, marker='o')
plt.show()
さて、ROCカーブは人が見れば性能の善し悪しがわかるものの、パソコンにこのROCカーブの画像を解析させるなんてことは大変です。何かしらの方法でROCカーブを数値化できれば良いのですが…… そこで賢い先人が考えたのがAUCという指標です。
AUC (Area Under the Curve)
Arakawa Under the Bridgeではありません、Area Under the Curveです。
呼び方はそのまま「えーゆーしー」が一般的であり、意味はROCカーブで描かれる面積です!
Scikit-learnであれば便利関数がすでに用意されています。
from sklearn.metrics import auc
print(f'AUC = {auc(fpr,tpr):.3f}')
AUC計算のスクラッチ実装
auc_score = 0
for i in range(len(fpr)-1):
auc_score += tpr[i] * (fpr[i+1]-fpr[i])
print(f'AUC = {auc_score:.3f}')
先程の分離度の良い・悪い2例についてAUCを計算してみると

このように分離度に従い
- 分離度の悪い分布のAUCは0.884
- 分離度の良い分布のAUCは0.998
と、分布の分離度が如実にAUCへ反映されていることがわかります。
ちなみにAUCの最大値は

アンサンブル実装!
ようやくモデルを評価するKPI的な指標を得た我々は、ついにアンサンブルモデルを適切に評価できるようになりました!
これで心置きなく様々なことにチャレンジできます。今回はモデルの学習方法についてはバギングやブースティングといった明確な学習方法があるので触れず、それらからできたモデル候補をどう組み合わせるか(ブレンディングやスタッキングと呼ばれる部分)を解説します。
良い組み合わせとはそれぞれの課題に対する各モデルの答えの信頼度を分析する作業と等価です。そのために今回は方法として下記4つを紹介します!
-
シンプルに合算して評価する(出力をそのまま信用する)
合算値 = モデル1出力+モデル2出力 -
モデルの正確度を評価する(出力に対して重みをつける)
合算値 = モデル1出力\times モデル1重み+モデル2出力\times モデル2重み -
モデルの正確度に加えて正確傾向も評価する(出力に対して非線形重みをつける)
合算値 = モデル1出力^{モデル1重み}+モデル2出力^{モデル2重み} -
モデルを独立した閾値で運用するメタモデルで評価する
合算値 = f(モデル1出力, モデル2出力)
0. 2モデルのサンプルデータを作る
先程までは1モデルの出力で評価していましたが、今回は2モデル以上必要なので、正規分布から下記のプログラムによって2モデル分の良品と不良品それぞれ25個の出力をシミュレートします。不良品のスコアについてはブースティング的なアンサンブル学習を想定しており、モデル1で苦手なものをモデル2で取れるようなスコアにしています。
今回はシンプルな変数で管理するのも大変なので、PandasのDataFrameにて管理する実装です。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc
np.random.seed(1)
num = 25
data = {}
data['name'] = [f"ok{i+1:02d}.png" for i in range(num)] + [f"ng{i+1:02d}.png" for i in range(num)]
data['ground-truth'] = [0]*num + [1]*num
data['model1'] = np.abs(np.concatenate([np.random.normal(1, 0.3, num), np.sort(np.random.normal(2, 2, num))]))
data['model2'] = np.abs(np.concatenate([np.random.normal(2, 0.5, num), np.sort(np.random.normal(2.5, 2, num))[::-1]]))
df = pd.DataFrame(data)
生成されるデータ
| name | ground-truth | model1 | model2 | |
|---|---|---|---|---|
| 0 | ok01.png | 0 | 1.48730360909897 | 2.15008515997791 |
| 1 | ok02.png | 0 | 0.816473075904977 | 1.82387507675324 |
| 2 | ok03.png | 0 | 0.841548474320963 | 1.42874090098893 |
| 3 | ok04.png | 0 | 0.678109413353148 | 1.82532863879356 |
| 4 | ok05.png | 0 | 1.2596222887974 | 1.89555288331261 |
| 5 | ok06.png | 0 | 0.309538390935915 | 2.29331159559109 |
| 6 | ok07.png | 0 | 1.52344352926494 | 2.41949170693725 |
| 7 | ok08.png | 0 | 0.771637929731469 | 2.46555104065177 |
| 8 | ok09.png | 0 | 1.09571172881712 | 2.14279366262712 |
| 9 | ok10.png | 0 | 0.925188887356777 | 2.44257058213536 |
| 10 | ok11.png | 0 | 1.43863238111349 | 1.62280102950167 |
| 11 | ok12.png | 0 | 0.381957787150703 | 2.62643407761664 |
| 12 | ok13.png | 0 | 0.903274838795947 | 2.256464910209 |
| 13 | ok14.png | 0 | 0.884783693599475 | 1.85095358244864 |
| 14 | ok15.png | 0 | 1.34013083270063 | 2.24425907326874 |
| 15 | ok16.png | 0 | 0.67003261980579 | 1.96221414348947 |
| 16 | ok17.png | 0 | 0.948271537734869 | 2.56581469372571 |
| 17 | ok18.png | 0 | 0.736642474623588 | 2.75990840821109 |
| 18 | ok19.png | 0 | 1.01266412401467 | 3.09278770326658 |
| 19 | ok20.png | 0 | 1.17484456411474 | 1.30175183225593 |
| 20 | ok21.png | 0 | 0.669814246836123 | 1.2779430972852 |
| 21 | ok22.png | 0 | 1.34341711295188 | 1.74776706852677 |
| 22 | ok23.png | 0 | 1.27047721617783 | 2.08001853472391 |
| 23 | ok24.png | 0 | 1.15074830167056 | 2.43808446055811 |
| 24 | ok25.png | 0 | 1.27025678477932 | 2.1578174736208 |
| 25 | ng01.png | 1 | 0.234620697270555 | 4.89783575980301 |
| 26 | ng02.png | 1 | 0.128461131481862 | 4.75896781582383 |
| 27 | ng03.png | 1 | 0.224742071830327 | 4.15594928521449 |
| 28 | ng04.png | 1 | 0.30958871700256 | 4.02402236062404 |
| 29 | ng05.png | 1 | 0.505683412498324 | 3.89606406814443 |
| 30 | ng06.png | 1 | 0.616678496549381 | 3.34698870812822 |
| 31 | ng07.png | 1 | 0.625654599760801 | 3.32010329441651 |
| 32 | ng08.png | 1 | 0.632544281651333 | 3.25512757264183 |
| 33 | ng09.png | 1 | 0.657507738326361 | 2.96018947072876 |
| 34 | ng10.png | 1 | 0.726008706861293 | 2.89659944025353 |
| 35 | ng11.png | 1 | 1.20649294628804 | 2.87312278197656 |
| 36 | ng12.png | 1 | 1.46422384074796 | 2.87031283496788 |
| 37 | ng13.png | 1 | 1.61632889527677 | 2.74364254198287 |
| 38 | ng14.png | 1 | 1.7542195489627 | 2.73801729161491 |
| 39 | ng15.png | 1 | 1.97467080216219 | 2.65468013669711 |
| 40 | ng16.png | 1 | 2.10161550955205 | 2.58719371366849 |
| 41 | ng17.png | 1 | 2.24031790496325 | 2.09848386214 |
| 42 | ng18.png | 1 | 2.38183096933493 | 2.05534371477928 |
| 43 | ng19.png | 1 | 2.46883139563418 | 1.88759197474325 |
| 44 | ng20.png | 1 | 3.06071093347637 | 1.81229264885784 |
| 45 | ng21.png | 1 | 3.23440621941483 | 1.74943009981977 |
| 46 | ng22.png | 1 | 3.48408832115467 | 1.25999831210374 |
| 47 | ng23.png | 1 | 5.31960435421974 | 1.22253918509155 |
| 48 | ng24.png | 1 | 5.38490920205549 | 1.15867542742193 |
| 49 | ng25.png | 1 | 6.20051027295768 | 1.544402431648 |
各モデルの出力をヒストグラムとROCカーブで図示すると……
描画用のプログラム
fig = plt.figure(figsize=(12,12))
ax = fig.add_subplot(2,2,1)
ok = df['model1'][df['ground-truth']==0]
ng = df['model1'][df['ground-truth']==1]
plt.hist([ok, ng], bins=25, color=['blue', 'red'], alpha=0.7, label=['OK','NG'])
plt.legend()
ax = fig.add_subplot(2,2,2)
fpr, tpr, _ = roc_curve([0]*len(ok)+[1]*len(ng), df['model1'])
plt.plot(fpr, tpr, marker='o', label=f'AUC = {auc(fpr,tpr):.3f}')
plt.legend()
ax = fig.add_subplot(2,2,3)
ok = df['model2'][df['ground-truth']==0]
ng = df['model2'][df['ground-truth']==1]
plt.hist([ok, ng], bins=25, color=['blue', 'red'], alpha=0.7, label=['OK','NG'])
plt.legend()
ax = fig.add_subplot(2,2,4)
fpr, tpr, _ = roc_curve([0]*len(ok)+[1]*len(ng), df['model2'])
plt.plot(fpr, tpr, marker='o', label=f'AUC = {auc(fpr,tpr):.3f}')
plt.legend()
plt.show()

各モデルのスコアのヒストグラムとROCカーブ (1行目:モデル1, 2行目:モデル2)
このようにそれぞれのモデルはちょっとポンコツっぽいことがわかります!
1. とりあえず信じてみる: 2モデルの合算
モデルたちの言うことがおおよそ正しいと信じられるのであれば、それらの合算あるいは平均といった出力も信頼に足るはずです。やってみましょう!式としてはこんな感じです。
# 合算によるアンサンブルスコア計算
ensemble_ok = df['model1'][df['ground-truth']==0] + df['model2'][df['ground-truth']==0]
ensemble_ng = df['model1'][df['ground-truth']==1] + df['model2'][df['ground-truth']==1]
この合計値でヒストグラムとROCカーブを描画してみると……

単純な合計でもかなり改善する様ですね!
しかしまだまだ精度的な改善の余地は大きそうです。
次はモデルの出力を独立した信用度的な評価を加えることで、それぞれの出力に適した重みを考えてみましょう!
2. どちらがエキスパート?: 2モデルの重みを調整する
複数の人間がいたとき、それぞれの経験年数であったり知識であったりで評価の確度が変わるのは当然の傾向と言えます。ここではそれらを「重み」で表現して合算値の改善に挑戦します。
ところで言うは易しですが、重みはどうやって決めるべきなのでしょうか?
いろいろな組み合わせを全部調べる?大変なように思いますが、パソコンさんであれば一瞬です。調べましょう!
全探索(グリッドサーチ)を実装する
すべてのパラメータ組み合わせを決められた範囲で全て調べることを全探索あるいはグリッドサーチと呼びます。2パラメータであれば愚直に2つのループを書けば良いのですが、ここではPython標準パッケージのitertoolsを使ったリストのデカルト積での1ループ表現を紹介します!(直積といっても実質2重ループなのですが、モデルやパラメータがもっとたくさん存在する場合に並列化が書きやすくなるので、エンジニアの方は覚えておいて損はないです。)
import itertools
from sklearn.metrics import roc_curve, auc, roc_auc_score
m1_weight = np.linspace(0.1,3,30) # 0.1~3.0まで30分割
m2_weight = np.linspace(0.1,3,30) # 0.1~3.0まで30分割
ground_truth = [0]*len(ensemble_ok)+[1]*len(ensemble_ng)
combination = []
for c in itertools.product(m1_weight, m2_weight): # 重みの組み合わせをリスト化
combination.append(c)
scores = []
for c in combination: # グリッドサーチ
scores.append(roc_auc_score(ground_truth, df['model1']*c[0]+df['model2']*c[1]))
# 最適重みの出力
best_weight = combination[np.argmax(scores)]
print(f"最適線形重み付け:{best_weight}, 最大AUC:{np.max(scores)}")
> 最適線形重み付け:(0.5, 0.6), 最大AUC:0.9872000000000001
すべての組み合わせに対してAUCが最大となる組み合わせはモデル1に0.5、モデル2に0.6の重みをかけたときのようです!
ちなみに重み組み合わせに対するAUCは下記のように可視化することも可能です。
plt.imshow(np.array(scores).reshape(len(m1_weight),-1)[::-1], extent=[0.1,3,0.1,3], cmap='jet')
plt.xlabel('Model 2 weight')
plt.ylabel('Model 1 weight')
plt.colorbar()
plt.show()

各モデルの重み組み合わせとAUCの対応関係
図から赤ほど性能が高いので、おおよそ2つのモデルでは同じような重みで良い傾向も確認できます。では早速求められた最適重みでROCカーブを描いてみると…
# 線形重みのアンサンブルスコア計算
ensemble_ok = df['model1'][df['ground-truth']==0]*best_weight[0] + df['model2'][df['ground-truth']==0]*best_weight[1]
ensemble_ng = df['model1'][df['ground-truth']==1]*best_weight[0] + df['model2'][df['ground-truth']==1]*best_weight[1]
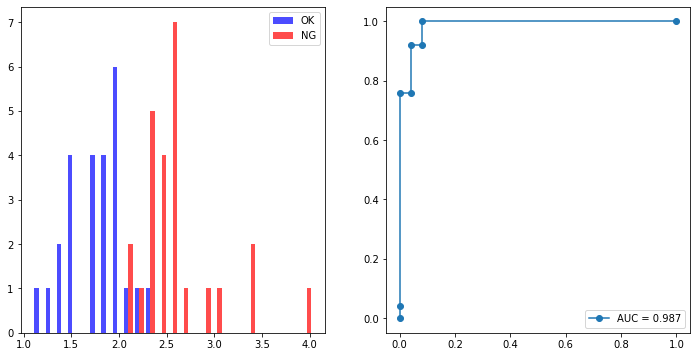
AUCは0.982→0.987と、ほんの僅かに良くなっていますね!
……もうちょっと何とかしましょうか
3. エキスパートにも個性あり: 2モデルの非線形な重みを調整する
先程はシンプルな重み計算をしていましたが、あまりにもシンプルであり、評価できているのはどちらのモデルをより信じるべきかという点のみでした。この場合、下記のようなオオカミ少年度的な信頼度を扱うことができません。
-
普段はおとなしいが、本当にやばい時は警告してくれるタイプの人
→ 高いスコアで高信頼性がある/一方でちょっとの異常ではスコアが低め -
普段からうるさいものの、言っていることはまぁまぁ当たるタイプの人
→ 低いスコアでもそこそこの信頼性がある/一方で真の異常に対してスコアが低め
い、一体こんなものをどうやって扱えば……
ここで思い出していただきたいのは指数関数です。指数関数を使えば、
- 値が大きくなるに連れて倍々ゲーム的に値を大きくしたり (指数が1以上)
- 値が小さくともカーブを描くように値を大きくしたり (指数が1以下)
できます!0~1で変化する数値に対して
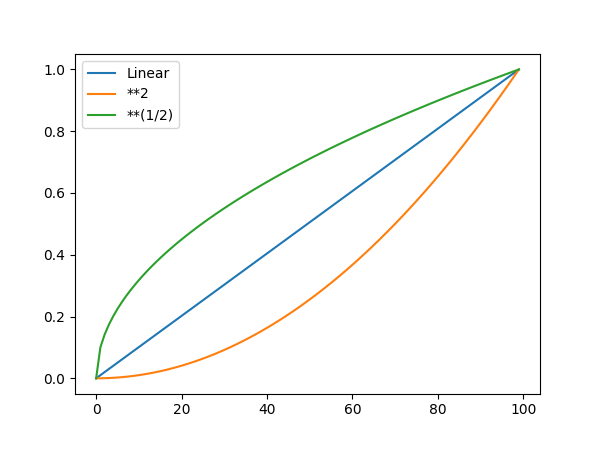
スコアに非線形重みづけしたプロット (**2が
傾向的には
これを合算値の式に組み込むと以下のようになります。
では同様に全探索してみましょう!
m1_weight = np.linspace(0.1,3,30)
m2_weight = np.linspace(0.1,3,30)
ground_truth = [0]*len(ensemble_ok)+[1]*len(ensemble_ng)
combination = []
for c in itertools.product(m1_weight, m2_weight):
combination.append(c)
scores = []
for c in combination:
scores.append(roc_auc_score(ground_truth, df['model1']**c[0]+df['model2']**c[1]))
best_weight = combination[np.argmax(scores)]
print(f"最適非線形重み付け:{best_weight}, 最大AUC:{np.max(scores)}")
plt.imshow(np.array(scores).reshape(len(m1_weight),-1)[::-1], extent=[0.1,3,0.1,3], cmap='jet')
plt.xlabel('Model 2 weight')
plt.ylabel('Model 1 weight')
plt.colorbar()
plt.show()
> 最適非線形重み付け:(2.0, 1.8), 最大AUC:0.9952

各モデルの非線形重み組み合わせとAUCの対応関係
最適化結果から察するに、サンプルの2モデルは普段はおとなしいタイプのようです!
先程よりも良さそうなので、これを可視化してみると……
# 非線形重みのアンサンブルスコア計算
ensemble_ok = df['model1'][df['ground-truth']==0]**best_weight[0] + df['model2'][df['ground-truth']==0]**best_weight[1]
ensemble_ng = df['model1'][df['ground-truth']==1]**best_weight[0] + df['model2'][df['ground-truth']==1]**best_weight[1]
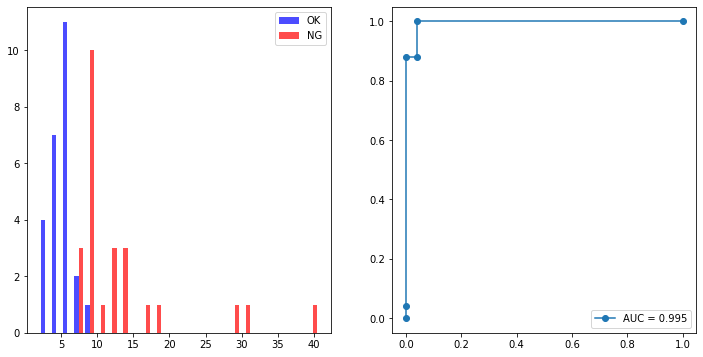
AUCは0.987→0.995と、さらに賢くなりました!
これで十分な気もしますが、さらなる高みを目指したい方は次のメタモデルに挑戦してみてください!
4. 貪欲法でシンプルなメタモデルを実装する
最後におまけ的な手法の紹介です!
1~3の方法では各モデルの出力を1つにまとめることで評価していましたが、「1つにまとめる」ということ自体が良くない場合もあります。文化祭の出し物でアイデア出しでは尖ったアイデアが出るものの、クラス全員の意向は喫茶店であったりお化け屋敷に落ち着く流れのように、アンサンブルモデルにおいても、モデルの数が増えるほど最終的な出力が平均化されていき、思ったほどの性能が出ないということになりえます。
そこで各々のエキスパートを各々の領域で活かすためにはモデルを運用するためのモデルを作ることが考えられ、今回は独立した閾値運用によるAUC最大化を目指すメタモデル実装例を紹介します。
問題定義として、「AUCを最大化する」とは「検出率を上げる際の過検出率を最小化する」 という問題であるため、手順としては
- 各々の閾値を各々の最大スコアで初期化
- 各モデルの合計値で上から順に未検出の画像を検出対象画像とする
- ある画像を検出する閾値をそれぞれのモデルで仮設定する
- その時の過検出率が低くなる方のモデルを調べる
- 過検出率が低くなる方のモデルを仮設定した閾値で更新する
- 画像リストの終わりまで2~5を繰り返す
のようになり、画像リストに対して行き当たりばったりで過検出率が低いモデルの閾値を更新していけばおおよそ良いことになります。この行き当たりばったり手法はコンピュータアルゴリズムの中では貪欲法と呼ばれる手法になり、常に最適解が求められるわけではありませんが、適切に運用すれば高速かつ高性能なアルゴリズムです。実装は以下のような雰囲気になります。
ok1 = np.array(df['model1'][df['ground-truth']==0])
ng1 = np.array(df['model1'][df['ground-truth']==1])
ok2 = np.array(df['model2'][df['ground-truth']==0])
ng2 = np.array(df['model2'][df['ground-truth']==1])
thresholds = {'m1':ng1.max(), 'm2':ng2.max()} # 各々の最大値で初期化
rank = list(np.argsort(ng1+ng2)[::-1]) # 合計値の高いものから検出
fpr = [0]
tpr = [0]
for i in rank:
fp1 = np.sum(ok1>ng1[i])
fp2 = np.sum(ok2>ng2[i])
if fp1 > fp2 and thresholds['m2'] > ng2[i]: # もしモデル2の過検出率が低ければ
thresholds['m2'] = ng2[i] # モデル2の閾値を更新
print(f"Update model2: {thresholds['m2']:.3f}")
elif fp2 > fp1 and thresholds['m1'] > ng1[i]: # もしモデル1の過検出率が低ければ
thresholds['m1'] = ng1[i] # モデル1の閾値を更新
print(f"Update model1: {thresholds['m1']:.3f}")
ensemble_fp = np.sum(np.logical_or(ok1>thresholds['m1'], ok2>thresholds['m2']))
ensemble_tp = np.sum(np.logical_or(ng1>thresholds['m1'], ng2>thresholds['m2']))
if ensemble_fp != fpr[-1]:
fpr.append(fpr[-1])
tpr.append(ensemble_tp)
fpr.append(ensemble_fp)
tpr.append(ensemble_tp)
if ensemble_fp == len(ng1):
break
fpr.append(fpr[-1])
tpr.append(len(ng1))
fpr.append(len(ok1))
tpr.append(len(ng1))
fpr = np.array(fpr)/len(ok1)
tpr = np.array(tpr)/len(ng1)
この結果を確認すると……
print(f"Model1 threshold: {thresholds['m1']:.3f}, Model2 threshold: {thresholds['m2']:.3f}")
plt.plot(fpr, tpr, marker='o', label=f'AUC = {auc(fpr,tpr):.3f}')
plt.legend()
plt.show()
> Model1 threshold: 1.616, Model2 threshold: 2.870
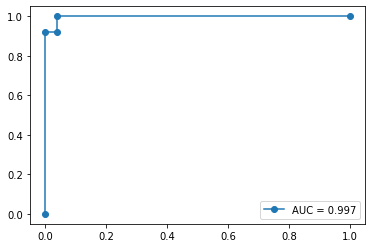
AUCは0.997まで改善しました! 今日は安心して眠れそうです。
まとめ: 問題を切り分けるアンサンブル
今回は機械学習モデルを組織的に運用するためのアンサンブルについて解説しました!
問題の大前提として機械学習モデルは万能ではなく、
- ある課題Aに対する性能を最大化するとき、課題Bの性能が低下する
- あるいは課題設定が広すぎて中に複数の利益相反関係の課題が存在する
というトレードオフが発生する場合があります。この問題を自動的に切り分ける/解消する手法の一つがアンサンブルです。
アンサンブルといっても様々ですが、大きく2手法に分類され、後者を重点的に解説しました。
- モデル自体の学習時に課題を分割する手法: バギング、ブースティングなど
- 課題に適したモデルを運用するモデルを考える手法: ブレンディング、スタッキングなど
運用段階では傾向の異なる複数の機械学習モデルを用意した上で
- それぞれ課題に対する各モデルの出力を信頼度ベースで重み付けをする
ことが基本戦略です。今回はその例として線形重み、非線形重み、独立閾値での運用手法を紹介しました。みなさんも 「何だか精度が出ない!」というときは課題のトレードオフを疑い、当記事を思い出してアンサンブルにトライしてみてください!
メンバー募集中です!
アダコテックでは随時メンバー募集中です!興味があれば一度弊社代表のノートをご確認ください!
Wantedlyやアダコテックのホームページにてエントリーも受付中です!
Discussion