特徴量エンジニアリングの道標
門脇大輔 阪田隆司 保坂桂佑 平松雄司 著
Kaggleで勝つデータ分析の技術
2019-10-09 技術評論社
https://gihyo.jp/book/2019/978-4-297-10843-4
polarsの練習も兼ねて、データの前処理と特徴量エンジニアリングについて網羅的にメモを残します。
ダミーのデータセットを基に相関のあるデータを作成し、このデータを使って遊んでいきます。
TL;DR
- 欠損値は平均で埋めるだけにせず、欠損かどうかのカテゴリ変数へ掃き出して、よりよい補完値で埋める。または埋めなくても良い手法で分析する。
- スケーリングは標準化だけではなく、順位や分布の裾野を見ながら最適なもの(モデルが扱いやすいもの)を選ぶ。
- カテゴリ変数のエンコーディングは、one-hot化やLabel Encodingだけでなく、精度重視ならTarget Encodingなども試す。
- 列同士の関係に対して事前知識がある場合、それを反映する演算で新しい特徴量を作る
次のライブラリを使う。
import numpy as np
from scipy import stats
import polars as pl
from matplotlib import pyplot as plt
import seaborn as sns
pl.Config(
tbl_cols=10,
tbl_rows=6,
tbl_hide_dataframe_shape=True,
tbl_hide_dtype_separator=True,
) # データフレームの表示設定
データ整形
サンプル注文のダミーデータを利用させてもらい、傾向を持つデータを作成する。
ダミーデータから傾向のあるデータを作成
data = pl.read_csv("datatable.csv")
# "entrydate", "birthday"を削除(今回は時間方向の話は考えないことにする)
data = data.drop("entrydate")
data = data.drop("birthday")
# "name": 氏名を英語名に変更
import random
import string
def randomname(n):
randlst = [random.choice(string.ascii_letters + string.digits) for _ in range(n)]
return ''.join(randlst)
new_seires = [randomname(random.randint(5,9)) for _ in range(len(data))]
data = data.drop("name")
data = data.with_columns(pl.Series("name", new_seires, dtype=pl.Int64))
# "diligent": 真面目さ ~ gaussian_mixture(π=[2,5,3], μ=[-2,0,3], σ=[1,1.5,1])
new_seires = np.concatenate([
stats.distributions.norm.rvs(loc=-5, scale=1, size=(200,1)),
stats.distributions.norm.rvs(loc=0, scale=1.5, size=(len(data)-500,1)),
stats.distributions.norm.rvs(loc=5, scale=1, size=(300,1))
])
np.random.shuffle(new_seires)
data = data.with_columns(pl.Series("diligent", new_seires.squeeze(), dtype=pl.Float32))
# "shiwa": 年齢"age"に相関する肌のしわしわ度合い
new_seires = np.round(data.select("age").to_numpy()**1.1 + stats.distributions.norm.rvs(loc=10, scale=20, size=(len(data),1)))
data = data.with_columns(pl.Series("shiwa", new_seires.squeeze(), dtype=pl.Int64))
# "bourgeois": 購入金額"totalmoney"とに相関するブルジョワ指数 (%)
totalmoney = data.select("totalmoney").to_numpy()/10000 + stats.distributions.norm.rvs(loc=0, scale=1, size=(len(data),1))
new_seires = (totalmoney - totalmoney.min())/(totalmoney.max() - totalmoney.min())*100
data = data.with_columns(pl.Series("bourgeois", new_seires.squeeze(), dtype=pl.Int64))
# "purchased": 真面目さ"diligent"とブルジョワ指数"bourgeois"に相関する購入品カテゴリ
diligent = data.select("diligent").to_numpy() + stats.distributions.norm.rvs(loc=0, scale=1, size=(len(data),1))
bourgeois = data.select("bourgeois").to_numpy() + stats.distributions.norm.rvs(loc=10, scale=2, size=(len(data),1))
new_seires = np.abs(diligent)*10 + bourgeois**1.5/5
new_seires = np.round((new_seires - new_seires.min())/(new_seires.max() - new_seires.min())*10).astype(np.int64)
goods = ["potatoes", "steak", "sushi", "shelves", "carpets", "wallpaper", "robots", "mansions", "jewelry", "airplane", "peace"]
new_seires = [goods[g] for g in new_seires.squeeze()]
# 女性で肌のシワシワ度が高い人は化粧品を買いやすい
new_seires = [
"cosmetics" if ((random.randint(0,10) > 4) and (s > 100) and (a == "women")) else p
for s, a, p in zip(data.select("shiwa").to_numpy(), data.select("seibetsu").to_numpy(), new_seires)
]
data = data.with_columns(pl.Series("purchased", new_seires))
# "seibetsu", "age", "shiwa"は無回答の場合欠損値が発生する
for i in range(len(data)):
if random.randint(0,50) == 0:
data[i, 1] = np.NaN
if random.randint(0,30) == 1:
data[i, 2] = np.NaN
if random.randint(0,50) == 2:
data[i, 6] = np.NaN
csvにするとこんな感じのデータになっている。
userid seibetsu age totalmoney name diligent shiwa bourgeois purchased
WG78242 men 64 63000 xHb3abbTf -5.843427 120 66 robots
RP38278 women 44 75000 ZPPD0xV0 0.62955105 82 65 wallpaper
VI99676 women 59 88000 RyHl4Uq -0.55146176 84 95 jewelry
YX43507 women 53 32000 Us5S8 -5.147211 82 35 carpets
CB13046 men 69 98000 wVVDxk1iU -4.810265 123 98 airplane
ZN62088 men 97000 fHNpwGt 4.4518375 115 86 jewelry
IU37978 women 66 22000 xzd6G4MzA 4.1738605 78 34 shelves
HA46319 women 46 42000 N7fR5 4.2387247 36 carpets
XM66346 NaN 18000 BO3CfJ -4.756428 97 18 shelves
FB46342 NaN 67 76000 Egn00wJm 4.1439805 139 57 wallpaper
デパートなんでも屋におけるユーザ情報と購入品目についてのデータを考えた。データは次の列をもち、欠損値も存在する。
-
userid: ユーザID -
name: ユーザ氏名 -
seibetsu: 性別 -
age: 年齢 -
totalmoney: 購入金額 -
diligent: 勤勉具合 -
shiwa: ユーザの肌のシワ -
bourgeois: ブルジョワ指数 -
purchased: 購入品目
# 可視化
print(data.columns, len(data))
print(data.head())
sns.pairplot(data.to_pandas(), hue="purchased")
['userid', 'seibetsu', 'age', 'totalmoney', 'name', 'diligent', 'shiwa', 'bourgeois', 'purchased'] 999
┌─────────┬──────────┬─────┬────────────┬───────────┬───────────┬───────┬───────────┬───────────┐
│ userid ┆ seibetsu ┆ age ┆ totalmoney ┆ name ┆ diligent ┆ shiwa ┆ bourgeois ┆ purchased │
│ str ┆ str ┆ i64 ┆ i64 ┆ str ┆ f32 ┆ i64 ┆ i64 ┆ str │
╞═════════╪══════════╪═════╪════════════╪═══════════╪═══════════╪═══════╪═══════════╪═══════════╡
│ WG78242 ┆ men ┆ 64 ┆ 63000 ┆ xHb3abbTf ┆ -5.843427 ┆ 120 ┆ 66 ┆ robots │
│ RP38278 ┆ women ┆ 44 ┆ 75000 ┆ ZPPD0xV0 ┆ 0.629551 ┆ 82 ┆ 65 ┆ wallpaper │
│ VI99676 ┆ women ┆ 59 ┆ 88000 ┆ RyHl4Uq ┆ -0.551462 ┆ 84 ┆ 95 ┆ jewelry │
│ YX43507 ┆ women ┆ 53 ┆ 32000 ┆ Us5S8 ┆ -5.147211 ┆ 82 ┆ 35 ┆ carpets │
│ CB13046 ┆ men ┆ 69 ┆ 98000 ┆ wVVDxk1iU ┆ -4.810265 ┆ 123 ┆ 98 ┆ airplane │
└─────────┴──────────┴─────┴────────────┴───────────┴───────────┴───────┴───────────┴───────────┘
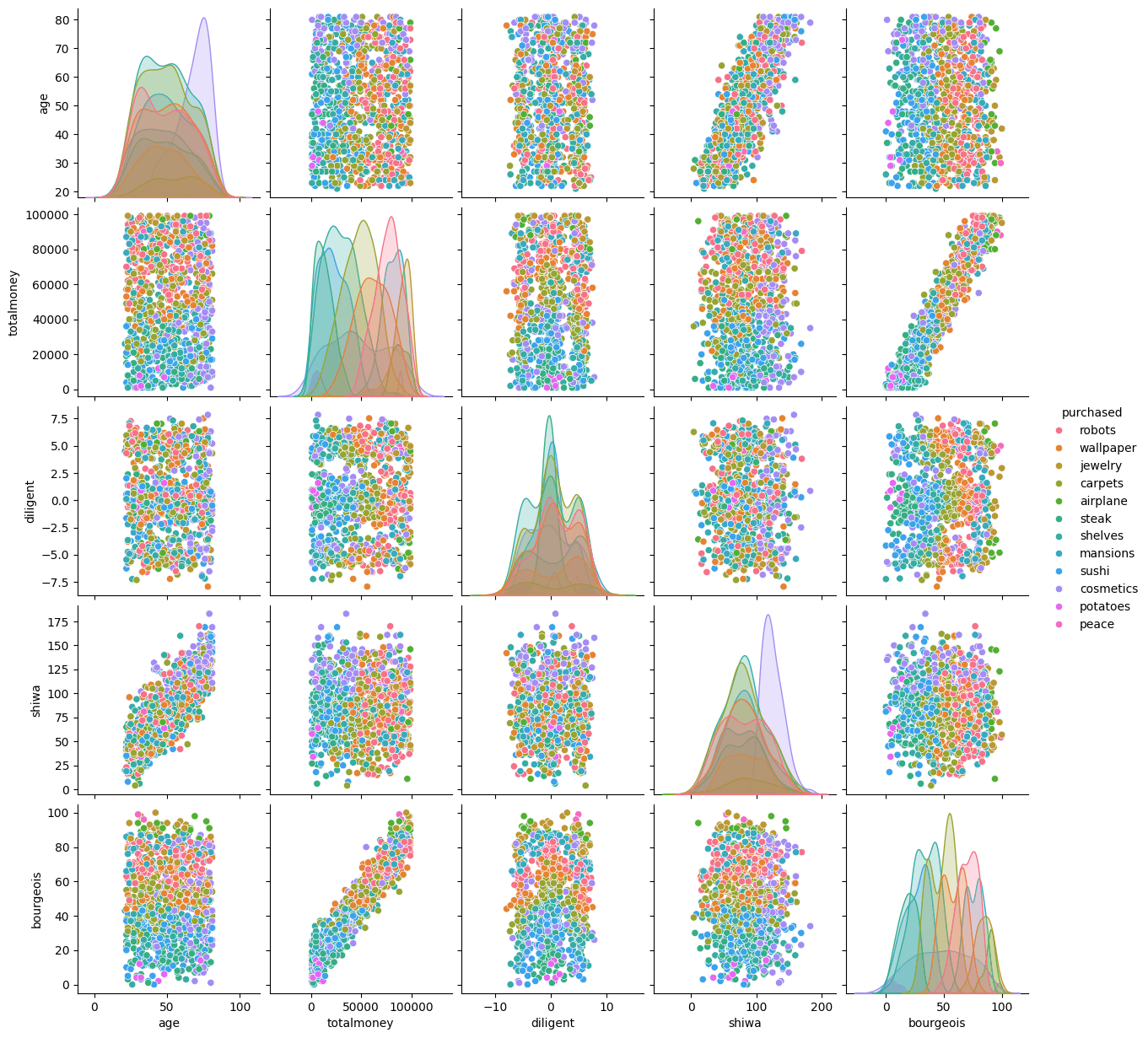
まず、このデータを使いやすいように最低限の整形を行う。
-
useridやnameのような今回の推論と関係ないデータを消す - カテゴリ変数である
seibetsuとpurchasedをOne-Hot Encodingする- 木ベースのモデルではLabel Encoding(カテゴリ変数を整数値に置き換える)ことも可能だが、その他のモデルではあまり望ましくない
- one-hot化より列数を抑えたい場合Feature Hashingが使えるが、あまり人気ではない
- カテゴリ変数の存在頻度でグループ分けするFrequency Encodingは、各カテゴリ変数と目的変数とに関連がある場合有効なことがある
- 各カテゴリ変数について、その値が所属する目的変数の平均でTarget Encodingすると良い場合もある
- カテゴリ変数が言語情報のときは言語モデルによりEmbedingのベクトルを変数にもちいることもある
特にTarget Encodingでは、今回元の問題の入力変数としてseibetsuがある。各seibetsuに属する目的変数を平均し、その値をカテゴリのLabel Encoding値として使う。(自身のラベルの情報を含まなように、out-of-foldで作ることに注意)
Label-Encodingにおいて、水準数が大きすぎる場合は疎行列として扱うこともある。
Encodingの実装
次のコードでは、カテゴリ変数の列のone-hot化、Label Encodingを試す。
ここでは欠損値は別のカテゴリ値として扱っている。
data = pl.read_csv("datatable_use.csv")
data = data.drop(["userid", "name"])
# One-Hot Encoding
data = data.with_columns(data.select(["seibetsu", "purchased"]).to_dummies())
data = data.drop(["seibetsu", "purchased"])
print(data.columns)
# ['age', 'totalmoney', 'diligent', 'shiwa', 'bourgeois', 'seibetsu_NaN', 'seibetsu_men', 'seibetsu_women', 'purchased_airplane', 'purchased_carpets', 'purchased_cosmetics', 'purchased_jewelry', 'purchased_mansions', 'purchased_peace', 'purchased_potatoes', 'purchased_robots', 'purchased_shelves', 'purchased_steak', 'purchased_sushi', 'purchased_wallpaper']
print(data)
# ┌─────┬────────────┬───────────┬───┬─────────────────┬─────────────────┬─────────────────────┐
# │ age ┆ totalmoney ┆ diligent ┆ … ┆ purchased_steak ┆ purchased_sushi ┆ purchased_wallpaper │
# │ i64 ┆ i64 ┆ f64 ┆ ┆ u8 ┆ u8 ┆ u8 │
# ╞═════╪════════════╪═══════════╪═══╪═════════════════╪═════════════════╪═════════════════════╡
# │ 64 ┆ 63000 ┆ -5.843427 ┆ … ┆ 0 ┆ 0 ┆ 0 │
# │ 44 ┆ 75000 ┆ 0.629551 ┆ … ┆ 0 ┆ 0 ┆ 1 │
# │ 59 ┆ 88000 ┆ -0.551462 ┆ … ┆ 0 ┆ 0 ┆ 0 │
# │ … ┆ … ┆ … ┆ … ┆ … ┆ … ┆ … │
# │ 51 ┆ 34000 ┆ -2.753193 ┆ … ┆ 0 ┆ 0 ┆ 0 │
# │ 24 ┆ 83000 ┆ -4.911862 ┆ … ┆ 0 ┆ 0 ┆ 0 │
# │ 47 ┆ 97000 ┆ -4.831748 ┆ … ┆ 0 ┆ 0 ┆ 0 │
# └─────┴────────────┴───────────┴───┴─────────────────┴─────────────────┴─────────────────────┘
# Label Encoding
seibetsu = data.select(["seibetsu_NaN", "seibetsu_men", "seibetsu_women"]).to_numpy()
data = data.with_columns(pl.Series("seibetsu", np.argmax(seibetsu, axis=1)))
purchased = data.select(["purchased_airplane", "purchased_carpets", "purchased_cosmetics", "purchased_jewelry", "purchased_mansions", "purchased_peace", "purchased_potatoes", "purchased_robots", "purchased_shelves", "purchased_steak", "purchased_sushi", "purchased_wallpaper"]).to_numpy()
data = data.with_columns(pl.Series("purchased", np.argmax(purchased, axis=1)))
data = data.drop(["seibetsu_NaN", "seibetsu_men", "seibetsu_women", "purchased_airplane", "purchased_carpets", "purchased_cosmetics", "purchased_jewelry", "purchased_mansions", "purchased_peace", "purchased_potatoes", "purchased_robots", "purchased_shelves", "purchased_steak", "purchased_sushi", "purchased_wallpaper"])
print(data)
# ┌─────┬────────────┬───────────┬───────┬───────────┬──────────┬───────────┐
# │ age ┆ totalmoney ┆ diligent ┆ shiwa ┆ bourgeois ┆ seibetsu ┆ purchased │
# │ i64 ┆ i64 ┆ f64 ┆ i64 ┆ i64 ┆ i64 ┆ i64 │
# ╞═════╪════════════╪═══════════╪═══════╪═══════════╪══════════╪═══════════╡
# │ 64 ┆ 63000 ┆ -5.843427 ┆ 120 ┆ 66 ┆ 1 ┆ 7 │
# │ 44 ┆ 75000 ┆ 0.629551 ┆ 82 ┆ 65 ┆ 2 ┆ 11 │
# │ 59 ┆ 88000 ┆ -0.551462 ┆ 84 ┆ 95 ┆ 2 ┆ 3 │
# │ … ┆ … ┆ … ┆ … ┆ … ┆ … ┆ … │
# │ 51 ┆ 34000 ┆ -2.753193 ┆ 81 ┆ 44 ┆ 1 ┆ 8 │
# │ 24 ┆ 83000 ┆ -4.911862 ┆ 55 ┆ 70 ┆ 2 ┆ 4 │
# │ 47 ┆ 97000 ┆ -4.831748 ┆ 70 ┆ 91 ┆ 1 ┆ 0 │
# └─────┴────────────┴───────────┴───────┴───────────┴──────────┴───────────
この段階でどの程度精度が出るか試してみる。
x = data.select(['age', 'totalmoney', 'diligent', 'shiwa', 'bourgeois', 'seibetsu']).to_numpy()
y = data.select(['purchased']).to_numpy()
print(x.shape, y.shape) # (999, 6) (999, 1)
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=1/8, shuffle=True)
from xgboost import XGBClassifier
bst = XGBClassifier(n_estimators=2, max_depth=16, learning_rate=1, objective="binary:logistic")
bst.fit(x_train, y_train)
y_pred = bst.predict(x_test)
from sklearn.metrics import confusion_matrix
from sklearn.metrics import f1_score
print(f1_score(y_test, y_pred, average="macro")) # 0.5558082681348402
cmx = confusion_matrix(y_test, y_pred)
sns.heatmap(cmx, annot=True)
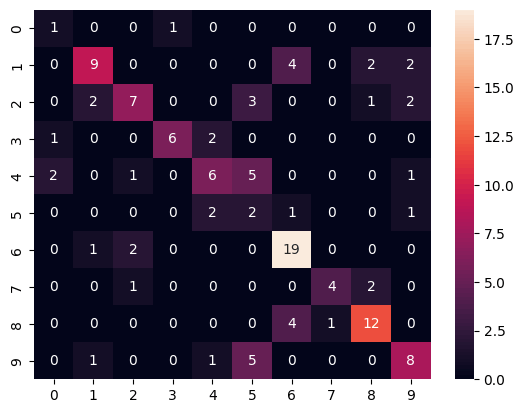
特徴量の整形
GBDTで扱うデータの整形を行う。GBDTでは数値の大きさではなく大小関係のみが影響し、欠損値があっても問題なく、変数間の相互作用もある程度反映してくれるので、変数の分布やスケールについてあまり考えなくて良い。
ただし、GLMやNNなどを使う場合はこれらが問題になるので、標準化や対数変換、欠損値の処理などを行う必要がある。
決定木の気持ちになって考える: Kagglerの名言。モデルに与えられている入力からは読み取れないデータを作ることが特徴量作成の肝で、例えばデータの別のテーブルの情報を結合したり、データの裏でユーザの行動が影響している場合にその特徴量を明示的に作って与えるなどが要る。
pnadasでは欠損値はNaNだが、polarsではNaNとNullを区別できる。
欠損値の補完
欠損値は単純に値として定義できないものや、ユーザが意図的に入力しなかったもの、値の取得に失敗したものなどが考えられる。
GBDTは欠損値をそのまま扱えるので、基本的には問題にならないが、埋めたほうが性能が出ることもあるのでどちらも試すべき。
欠損値のあるレコードを捨ててしまう方法もあるが、テストデータに欠損値がある場合はそれでは良くない。
- 欠損値を表現する極端な値で埋める
- 平均や中央値で埋める
- 分布が歪んでいる場合は対数変換などで歪を均してから埋める
- 不均衡データのカテゴリ変数はそのクラス毎平均も信用できないので、Bayesian Averageを使う
- 欠損値を欠損のないデータから予測する
- 欠損値はランダムではなくなにか欠損が起こる原因がある場合が考えられるため、欠損値かどうかを新たな特徴量として与える
Bayesian Averageは事前の信念を与えることで、極端な観測データに対しても信念を考慮した平均値を計算する平均方法。次の式によって表され、あらかじめm個の値
また、予測値を欠損に使う場合、欠損値の入力変数に本来の目的値は含めないことに注意。テストデータの推論で使えない手法になってしまう。
変数のスケーリング
木ベースモデルでは関係ないが、ロジスティック回帰などのGLMや、画像においてもNN系手法などを使うときは標準化(standardization)により平均と分散を揃えておくことが推奨される。
Min-Maxスケーリングで0~1に揃えることもあるが、外れ値があると他の値が強く影響を受けてしまうので、個人的にはあまりやらない。
また、分布の形そのものを変える方法として非線形変換を行う次のもある。
- 対数変換: ロングテールな分布がある変数に対してこれを行うと、情報を集約できる。実用上ゼロを避けるため
\log(|x|+1) np.log1p(x)が使われる。 - Box-Cox変換: 対数変換を
λ=0 - Yeo-Johnson変換: 負の数にも対応したBox-Cox変換のlog1p版
関数適用だけでなく、量子化してレベルセットに分ける方法や、順位への変換などが使われることもある。
- Rank-Gauss: 数値データを順位に変換した後、順序を保ちながらガウス分布に従うように変形する。NN系手法への入力として使われたことがある
特徴量の変換
欠損値を新たな列に掃き出して、代わりに他の列からの予測値を使って埋める。
# "age"と"shiwa"の欠損値を予測
# (単純な欠損値補完なら data.fill_null(val))で完了する
data_null, data_fill = data.filter(pl.col("age").is_null()), data.filter(pl.col("age").is_not_null())
x_train = data_fill.select(["totalmoney", "diligent", "shiwa", "bourgeois", "seibetsu"]).to_numpy()
y_train = data_fill.select(["age"]).to_numpy()
x_test = data_null.select(["totalmoney", "diligent", "shiwa", "bourgeois", "seibetsu"]).to_numpy()
print(x_train.shape, y_train.shape, x_test.shape) # (969, 5) (969, 1) (30, 5)
from xgboost import XGBRegressor
bst = XGBRegressor(n_estimators=2, max_depth=16, learning_rate=1, objective="reg:squarederror")
bst.fit(x_train, y_train)
y_pred = bst.predict(x_test)
data_null = data_null.with_columns(pl.Series("age", np.round(y_pred), dtype=pl.Int64))
data_fillnull = pl.concat([data_fill, data_null])
data_null, data_fill = data_fillnull.filter(pl.col("shiwa").is_null()), data_fillnull.filter(pl.col("shiwa").is_not_null())
x_train = data_fill.select(["totalmoney", "diligent", "age", "bourgeois", "seibetsu"]).to_numpy()
y_train = data_fill.select(["shiwa"]).to_numpy()
x_test = data_null.select(["totalmoney", "diligent", "age", "bourgeois", "seibetsu"]).to_numpy()
print(x_train.shape, y_train.shape, x_test.shape) # (976, 5) (976, 1) (23, 5)
bst = XGBRegressor(n_estimators=2, max_depth=16, learning_rate=1, objective="reg:squarederror")
bst.fit(x_train, y_train)
y_pred = bst.predict(x_test)
data_null = data_null.with_columns(pl.Series("shiwa", np.round(y_pred), dtype=pl.Int64))
data_fillnull = pl.concat([data_fill, data_null])
print(data_fillnull)
┌─────┬────────────┬───────────┬───────┬───────────┬──────────┬───────────┐
│ age ┆ totalmoney ┆ diligent ┆ shiwa ┆ bourgeois ┆ seibetsu ┆ purchased │
│ i64 ┆ i64 ┆ f64 ┆ i64 ┆ i64 ┆ i64 ┆ i64 │
╞═════╪════════════╪═══════════╪═══════╪═══════════╪══════════╪═══════════╡
│ 64 ┆ 63000 ┆ -5.843427 ┆ 120 ┆ 66 ┆ 1 ┆ 7 │
│ 44 ┆ 75000 ┆ 0.629551 ┆ 82 ┆ 65 ┆ 2 ┆ 11 │
│ 59 ┆ 88000 ┆ -0.551462 ┆ 84 ┆ 95 ┆ 2 ┆ 3 │
│ … ┆ … ┆ … ┆ … ┆ … ┆ … ┆ … │
│ 78 ┆ 49000 ┆ -3.593774 ┆ 124 ┆ 42 ┆ 1 ┆ 8 │
│ 43 ┆ 80000 ┆ 7.0384526 ┆ 81 ┆ 94 ┆ 2 ┆ 0 │
│ 30 ┆ 12000 ┆ 4.2189426 ┆ 54 ┆ 35 ┆ 1 ┆ 8 │
└─────┴────────────┴───────────┴───────┴───────────┴──────────┴───────────┘
また、Rank-Gauss変換を使ってdiligentの分布を見てみる。こちらは分布がおかしなデータでも、正規分布の形状にできる。
from sklearn.preprocessing import QuantileTransformer
qt = QuantileTransformer(n_quantiles=100, output_distribution="normal") # "uniform"なら順位への変換と等価
d1 = data_fillnull.select("diligent").to_numpy()
d2 = qt.fit_transform(d1)
fig, axes = plt.subplots(1, 2, figsize=(10,4))
axes[0].hist(d1.squeeze())
axes[1].hist(d2.squeeze())
fig.show()
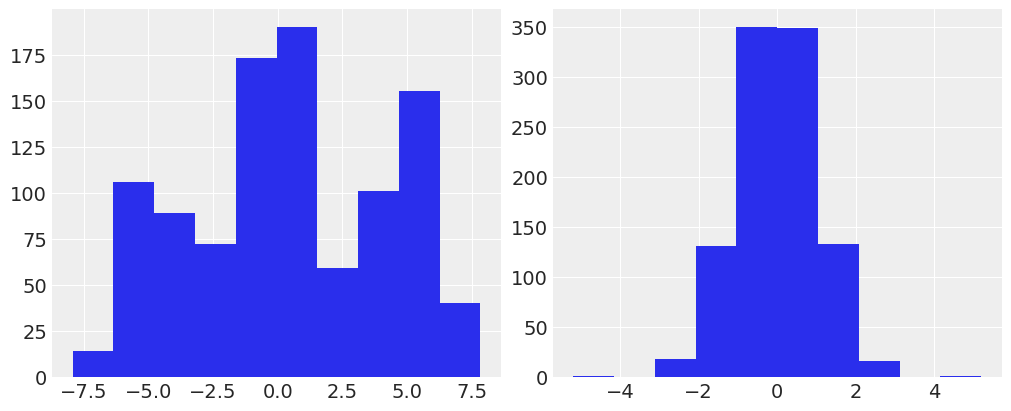
特徴量を増やす
変数をかけ合わせる
量的変数とカテゴリ変数を使って新たな特徴量の列を作る。
例えば、カテゴリ変数の各レベルセットに対する統計量を取って、量的変数の持つ情報を強化する方法などがある。
量的変数同士をかけ合わせる
積商からある列の単位量あたりの量を計算するなどができる。GBDTは和の分離は容易だが、積の分離は列の条件分岐がいるので容易ではないとKDTの筆者は分析しており、和ではなく積が効果的であることを示唆している。
カテゴリ変数同士をかけ合わせる
Target Encodingによるエンコードと組み合わせることで、目的変数の平均のグループが細分化されて特徴をつかみやすい列を作りやすい。
ただしレベルセットの大きさが大きすぎると良くないので注意。
行の特徴を使う
レコードごとに欠損値やゼロをカウントすることで、なにか特徴が現れるかもしれない。また、ユーザの特性を表しそうなアイテム、例のデータでは、購入商品cosmeticsなどについてあらかじめ考慮する特徴を与えられれば、データの解析に貢献する。
特徴量を減らす
PCAやNMFなどで情報量(特徴量のもつ分散)を残しながら新しい列に変換する。ただし説明性は低くなるのであくまで学習アルゴリズムの計算量に関して現実的でない場合のみ行うという印象。
ほかにもトピックモデルなどで使われるLatent Dirichlet Allocation(LDA)や、分類タスクで使われるLinear Discriminsny Analysis(LDA)などもある。ベイズ的なLDAについては以下に理論面と実装を書いた。
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA, NMF, LatentDirichletAllocation
x = data_fillnull.select(['age', 'totalmoney', 'diligent', 'shiwa', 'bourgeois', 'seibetsu']).to_numpy()
y = data_fillnull.select(['purchased']).to_numpy()
print(x.shape, y.shape) # (999, 6) (999, 1)
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=1/8, shuffle=True)
# PCAによる分散sort
stdscaler = StandardScaler()
x_train = stdscaler.fit_transform(x_train)
x_test = stdscaler.transform(x_test)
pca = PCA()
x_train = pca.fit_transform(x_train)
x_test = pca.transform(x_test)
print(pca.explained_variance_ratio_)
# [0.32747653 0.30090986 0.1706861 0.16020666 0.03213623 0.00858462]
explained_variance_ratio_で空間軸の分散説明割合を見ることができる。この例では6つの特徴量のうち、空間軸を変えることで4列で95%の分散を説明できることがわかった。
今回の例のようなデータは次元を減らすことにご利益はないが、何万次元のデータを使って精度を出したい場合、チューニングなどが重くなるのでデータを予め分解し、99%以下は捨てるというような方法でかなりの計算リソースを省エネできる。
可視化
PCAにより2次元まで減らすのは、あまり現実的ではない(明確に区別できるほどクラスタに分けられない)。
t-SNEやさらに新しいUMAPで可視化すると、クラスタなどを人間の直感と照らし合わせて分析することができる。可視化だけでなく、特徴量として付け加えることで精度に大きく貢献することもある。
import bhtsne
import umap # pip install umap-learn
# emb.shape: (999, 2)
stdscaler = StandardScaler()
array_std = stdscaler.fit_transform(data_fillnull.drop("purchased").to_numpy())
target = data_fillnull.select("purchased").to_numpy().astype(np.uint8)
emb = bhtsne.tsne(array_std.astype(np.float64))
plt.scatter(x=emb[:,0], y=emb[:,1], c=target)
plt.show()
um = umap.UMAP()
emb = um.fit_transform(array_std)
plt.scatter(x=emb[:,0], y=emb[:,1], c=target)
plt.show()
 左がt-SNE、右がUMAPによる2次元空間への埋め込み
左がt-SNE、右がUMAPによる2次元空間への埋め込み
体感UMAPの方が新しいこともあり、高速に感じた。
テスト
最後にこれらを合わせてどの程度性能が改善したか見てみる。ただし、特徴量エンジニアリング以前以後両方とも何度か学習を試行したうちのチャンピオンモデルの結果を載せており、ハイパラ調整など個なった厳密な比較ではないことに注意。
embs = pl.DataFrame({
"rank": d2[:,0],
"emb1": emb1[:,0],
"emb2": emb1[:,1],
"emb3": emb2[:,0],
"emb4": emb2[:,1]
})
data_fin = data_fillnull.with_columns(embs)
with pl.Config(tbl_cols=7):
print(data_fin)
# ┌─────┬────────────┬───────────┬───────┬───┬────────────┬───────────┬───────────┐
# │ age ┆ totalmoney ┆ diligent ┆ shiwa ┆ … ┆ emb2 ┆ emb3 ┆ emb4 │
# │ i64 ┆ i64 ┆ f64 ┆ i64 ┆ ┆ f64 ┆ f32 ┆ f32 │
# ╞═════╪════════════╪═══════════╪═══════╪═══╪════════════╪═══════════╪═══════════╡
# │ 64 ┆ 63000 ┆ -5.843427 ┆ 120 ┆ … ┆ -23.452218 ┆ 15.361952 ┆ 6.503043 │
# │ 44 ┆ 75000 ┆ 0.629551 ┆ 82 ┆ … ┆ 13.366962 ┆ 0.111078 ┆ 4.471266 │
# │ 59 ┆ 88000 ┆ -0.551462 ┆ 84 ┆ … ┆ 9.304404 ┆ -0.043195 ┆ 3.848367 │
# │ … ┆ … ┆ … ┆ … ┆ … ┆ … ┆ … ┆ … │
# │ 78 ┆ 49000 ┆ -3.593774 ┆ 124 ┆ … ┆ -11.061478 ┆ 16.200331 ┆ 7.017477 │
# │ 43 ┆ 80000 ┆ 7.0384526 ┆ 81 ┆ … ┆ 16.268805 ┆ -0.728551 ┆ 5.496882 │
# │ 30 ┆ 12000 ┆ 4.2189426 ┆ 54 ┆ … ┆ -7.583622 ┆ 15.0792 ┆ 10.301356 │
# └─────┴────────────┴───────────┴───────┴───┴────────────┴───────────┴───────────┘
x = data_fin.select(['age', 'totalmoney', 'diligent', 'shiwa', 'bourgeois', 'seibetsu', 'rank', 'emb1', 'emb2', 'emb3', 'emb4']).to_numpy()
y = data_fin.select(['purchased']).to_numpy()
print(x.shape, y.shape) # (999, 11) (999, 1)
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=1/8, shuffle=True)
from xgboost import XGBClassifier
bst = XGBClassifier(n_estimators=2, max_depth=16, learning_rate=1, objective="binary:logistic")
bst.fit(x_train, y_train)
y_pred = bst.predict(x_test)
from sklearn.metrics import confusion_matrix
from sklearn.metrics import f1_score
print(f1_score(y_test, y_pred, average="macro")) # 0.5764721102652136
cmx = confusion_matrix(y_test, y_pred)
sns.heatmap(cmx, annot=True)
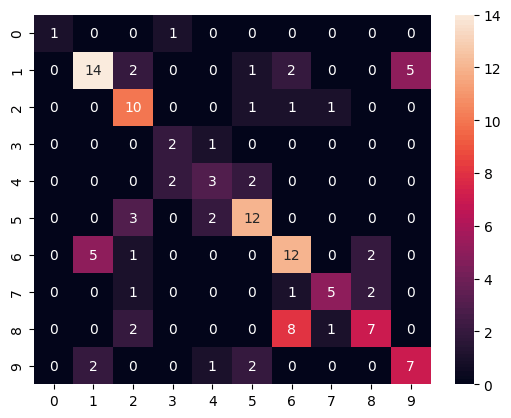
正直あまり効果は見られない。ほんの少しましになったものの、試行回数が十分あればノイズ程度の差の可能性もある。また、もとよりデータ生成プロセスに関して効きそうな特徴量整形はしておらず、今回試したものはあくまでベースライン程度の意味しかないという考え方もできる。
感想
この記事は単純な手法を列挙しただけだが、本を読み、改めてデータ(特徴量)の整形には非常に深いドメイン知識がられることがわかった。
手法を知っているだけではなにもできないところが多い。データを生成しているプロセス(どの特徴がどの値を取っていて、どの列と関係しているか)に関して考察して形作っていく必要があるため、数理的な理論を理解しているだけでなく、それを適用できるシチュエーションを判断できるうえで、データの深い部分の理解を使って特徴量を扱うことが、分析に必要となってくる。
Discussion